鲁教版(五四制)七年级数学下册第十一章 一元一次不等式与不等式组重点解析练习题 含解析
文档属性
| 名称 | 鲁教版(五四制)七年级数学下册第十一章 一元一次不等式与不等式组重点解析练习题 含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览




文档简介
七年级数学下册第十一章一元一次不等式与不等式组重点解析
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如果a>b,那么下列不等式中正确的是( )
A.a-b>0 B.ac >bc C.c-a>c-b D.a+3<b-3
2、若关于的一元一次不等式组的解集为,且关于的方程的解为非负整数,则符合条件的所有整数的和为( )
A.2 B.7 C.11 D.10
3、已知,那么下列各式中,不一定成立的是( )
A. B. C. D.
4、若,则下列式子一定成立的是( )
A. B. C. D.
5、若点在第一象限,则a的取值范围是( )
A. B. C. D.无解
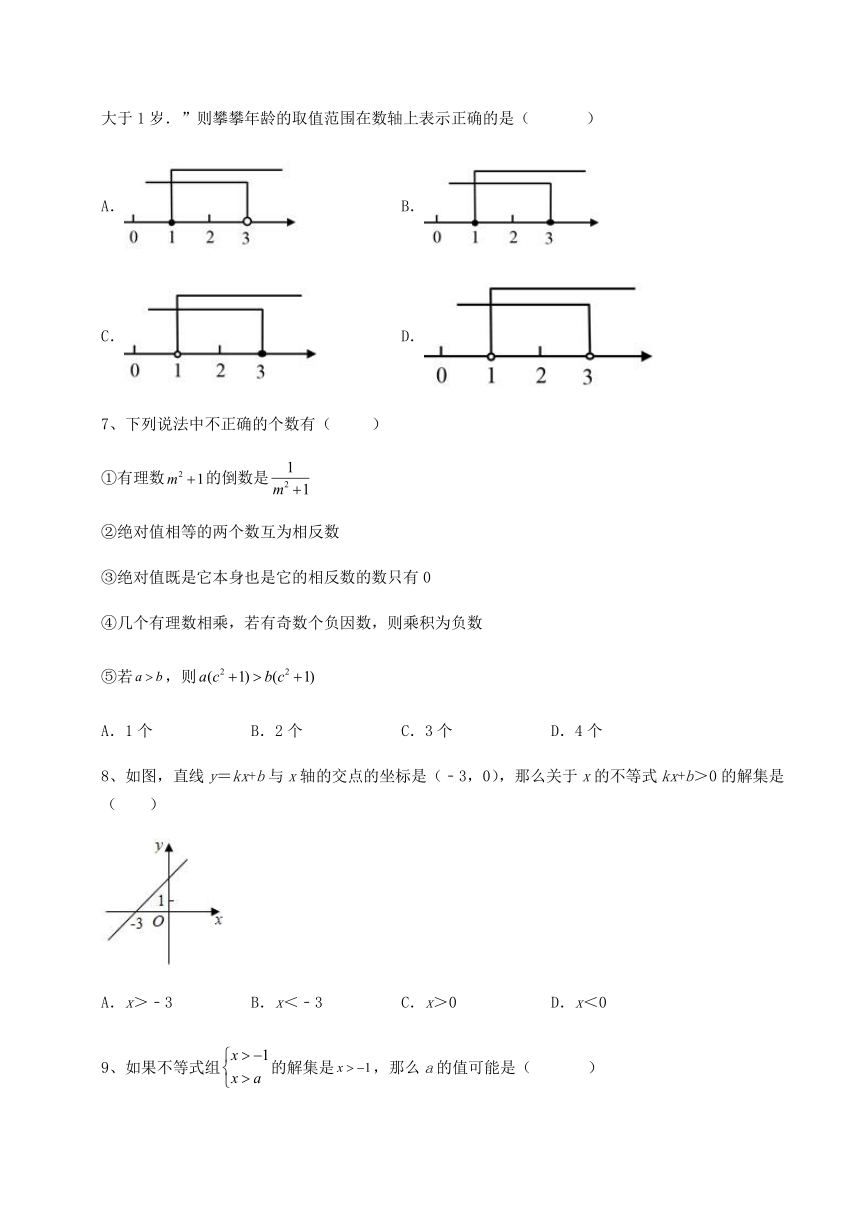
6、某天,孟孟与欢欢在讨论攀攀的年龄,欢欢说:“攀攀至多3岁.”而孟孟说:“攀攀的年龄一定大于1岁.”则攀攀年龄的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7、下列说法中不正确的个数有( )
①有理数的倒数是
②绝对值相等的两个数互为相反数
③绝对值既是它本身也是它的相反数的数只有0
④几个有理数相乘,若有奇数个负因数,则乘积为负数
⑤若,则
A.1个 B.2个 C.3个 D.4个
8、如图,直线y=kx+b与x轴的交点的坐标是(﹣3,0),那么关于x的不等式kx+b>0的解集是( )
A.x>﹣3 B.x<﹣3 C.x>0 D.x<0
9、如果不等式组的解集是,那么a的值可能是( )
A.-2 B.0 C.-0.7 D.
10、将不等式的解集表示在数轴上,正确的是( )
A. B.
C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、像这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个__________.
2、我们把几个一元一次不等式解集的__________,叫作由它们所组成的一元一次不等式组的解集.
3、如图,直线y=kx+b交坐标轴于A,B两点,则关于x的不等式kx+b<0的解集是_____.
4、不等式的最大整数解是_______.
5、若实数满足,则的取值范围为___________.
三、解答题(5小题,每小题10分,共计50分)
1、说出下列不等式变形的依据:
(1)由x-1>2,得x>3;
(2)由-2x>-4,得x<2;
(3)由-x<-1,得x>2;
(4)由3x<x,得2x<0.
2、在近几年的两会中,有多位委员不断提出应在中小学开展编程教育,2019年3月教育部公布的《2019年教育信息化和网络安全工作要点》中也提出将推广编程教育.某学校的编程课上,一位同学设计了一个运算程序,如图所示.按上述程序进行运算,程序运行到“判断结果是否大于23”为一次运行.
(1)若,直接写出该程序需要运行 次才停止;
(2)若该程序只运行了1次就停止了,则的取值范围是 .
(3)若该程序只运行了2次就停止了,求的取值范围.
3、仔细阅读下面例题,解答问题:
观察下列各计算题:
26×682=286×62
34×473=374×43
52×275=572×25
15×561=165×51
……
以上每个等式都非常巧妙,左边是一个两位数乘以三位数,等式两边的数字之间具有特殊性,一边的数字也有特殊性,且数字关于等号成对称分布,我们把满足这种条件的等式称为“对称积等式”.
(1)解决问题:填空,使下列各式成为“对称积等式”:41×154= ×14; ×286=682×
(2)解决问题:设“对称积等式”这类等式左边两位数的十位数字为a,个位数字为b,
①写出a+b的取值范围;
②请用含a、b的代数式写出表示“对称积等式”的式子,并证明你的结论.
4、解不等式:,并把它的解集在数轴上表示出来.
5、某商场同时购进甲乙两种商品共300件,其进价和售价如下表,设购进甲种商品x件,销售完300件商品的总利润为y元.
商品名称 甲 乙
进价(元/件) 50 70
售价(元/件) 90 120
(1)求y与x的函数关系式.
(2)该商品计划最多投入17000元用于购买这两种商品,若售完这些商品,则至少购进多少件甲商品商场可获得最大利润,获得的最大利润是多少元?
-参考答案-
一、单选题
1、A
【解析】
【分析】
在不等式的两边都加上或减去同一个数或整式,不等号的方向不变,在不等式的两边都乘以或除以同一个正数,不等号的方向不变,在不等式的两边都乘以或除以同一个负数,不等号的方向改变,根据不等式的基本性质逐一分析即可.
【详解】
解: a>b,
故A符合题意;
a>b,
当时, 故B不符合题意;
a>b,
故C不符合题意;
a>b,
故D不符合题意;
故选A
【点睛】
本题考查的是不等式的基本性质,掌握“不等式的基本性质”是解本题的关键.
2、B
【解析】
【分析】
先解关于的一元一次不等式组,再根据其解集是,得小于5;再解方程,根据其有非负整数解,得出的值,再求积即可.
【详解】
解:由,得:,
由,得:,
不等式组的解集为,
,
解得;
解关于的方程得:,
方程的解为非负整数,
或3或6或9,
解得或2或3.5或5,
所以符合条件的所有整数的和,
故选:B.
【点睛】
此题考查了解一元一次不等式组及一元一次方程的解,熟练掌握各自的解法是解本题的关键.
3、A
【解析】
【分析】
根据不等式的性质1不等式不等式两边同时加或减去同一个数或整式,不等号方向不变,基本性质2:不等式两边同时乘以(或除以)同一个大于0的整数,不等号方向不变 基本性质3:不等式两边同时乘以(或除以)同一个小于0的整数,不等号方向改变,根据不等式性质对各选项进行一一分析判断即可.
【详解】
解:.,不妨设,
则,
选项符合题意;
B.,
,
选项B不符合题意;
C.,
,
,
选项C不符合题意;
D.,
,
,
选项D不符合题意;
故选:A.
【点睛】
本题考查不等式性质,掌握不等式性质是解题关键.
4、B
【解析】
【分析】
根据不等式的性质依次分析判断.
【详解】
解:∵,∴a+1>b+1,故选项A不符合题意;
∵,∴,故选项B符合题意;
∵,∴-2a<-2b,故选项C不符合题意;
∵,∴,故选项D不符合题意;
故选:B.
【点睛】
此题考查了不等式的性质:不等式两边同时加上或减去同一个整式,不等号方向不变;不等式两边同时乘或除以同一个不为0的整正数,不等号方向不变;不等式两边同时乘或除以同一个不为0的负数,不等号方向改变.
5、B
【解析】
【分析】
由第一象限内的点的横纵坐标都为正数,可列不等式组,再解不等式组即可得到答案.
【详解】
解: 点在第一象限,
由①得:
由②得:
故选B
【点睛】
本题考查的是根据点所在的象限求解字母的取值范围,掌握坐标系内点的坐标特点是解本题的关键.
6、C
【解析】
【分析】
由至多得到小于等于,结合大于得到答案.
【详解】
解:由题意得,攀攀的年龄大于1且小于等于3,
故选:C.
【点睛】
此题考查了在数轴上表示不等式的解集,正确掌握大于、大于等于、小于等于的不同表示方法是解题的关键.
7、B
【解析】
【分析】
由倒数的定义可判断①,由绝对值的含义可判断②③,由有理数的乘法中积的符号确定方法可判断④,由不等式的基本性质可判断⑤,从而可得答案.
【详解】
解:因为 所以有理数的倒数是,故①正确;不符合题意
绝对值相等的两个数互为相反数或者相等,故②不正确;符合题意;
绝对值既是它本身也是它的相反数的数只有0,故③正确;不符合题意;
几个不为零有理数相乘,若有奇数个负因数,则乘积为负数,若其中一个因数为0,则结果为0,故④不正确;符合题意;
若,则,故⑤正确;不符合题意;
所以②④符合题意
故选: B.
【点睛】
本题考查的是倒数的含义,绝对值的含义,有理数乘法中积的符号确定,不等式的性质,掌握以上基础知识是解本题的关键.
8、A
【解析】
【分析】
根据图象直接解答即可.
【详解】
∵直线y=kx+b与x轴交点坐标为(﹣3,0),
∴由图象可知,当x>﹣3时,y>0,
∴不等式kx+b>0的解集是x>﹣3.
故选:A.
【点睛】
此题考查了一次函数图象与不等式的关系,不等式的解集即为一次函数的函数值大于零、等于零或小于零,正确理解二者之间的关系是解题的关键.
9、A
【解析】
【分析】
根究不等式组解集的确定原则,判定a≤-1,比较大小后,确定即可.
【详解】
∵不等式组的解集是,
∴a≤-1,
只有-2满足条件,
故选A.
【点睛】
本题考查了不等式组解集,正确理解不等式组解集的确定原则是解题的关键.
10、D
【解析】
【分析】
先求出不等式的解集,然后画出数轴,并在数轴上表示出不等式的解集.
【详解】
解:,
解得:,
表示在数轴上,如图所示:
.
故选:D.
【点睛】
本题考查了一元一次不等式的解法,熟练掌握解一元一次不等式的步骤是解答本题的关键.不等式的解集在数轴上表示时,空心圈表示不包含该点,实心点表示包含该点.
二、填空题
1、一元一次不等式组
【解析】
略
2、公共部分
【解析】
略
3、x<-2
【解析】
【分析】
根据图象,找出在x轴下方的函数图象所对应的自变量的取值即可得答案.
【详解】
∵点A坐标为(-2,0),
∴关于x的不等式kx+b<0的解集是x<-2,
故答案为:x<-2
【点睛】
本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合;熟练掌握函数图象法是解题关键.
4、2
【解析】
【分析】
首先根据不等式求解不等式,再根据不等式的解集写出最大的整数解.
【详解】
解:移项,得:,
合并同类项,得:,
系数化成1得:,
则最大整数解是:2.
故答案是:2.
【点睛】
本题主要考查不等式的整数解,关键在于求解不等式.
5、
【解析】
【分析】
先根据已知等式可得,从而可得,再根据绝对值的非负性、偶次方的非负性求出的取值范围,由此即可得出答案.
【详解】
解:由得:,
则,
,
,解得,
又,
,
,
即的取值范围为,
故答案为:.
【点睛】
本题考查了绝对值的非负性、偶次方的非负性、一元一次不等式组的应用,熟练掌握绝对值和偶次方的非负性是解题关键.
三、解答题
1、 (1)见解析
(2)见解析
(3)见解析
(4)见解析
【解析】
【分析】
(1)根据等式两边加上(或减去)同一个数,不等号方向不变求解;
(2)根据不等式两边乘以(或除以)同一个负数,不等号方向改变求解;
(3)根据不等式两边乘以(或除以)同一个负数,不等号方向改变求解;
(4)根据等式两边加上(或减去)同一个含有字母的式子,不等号方向不变求解.
(1)
解:由x-1>2,得x>3,不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;
(2)
解:由-2x>-4,得x<2,不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;
(3)
解:由-x<-1,得x>2,不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;
(4)
解:由3x<x,得2x<0,不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.
【点睛】
本题主要考查了不等式的性质,正确掌握不等式的性质是解题关键.
2、 (1)4
(2)
(3)
【解析】
【分析】
(1)当时,根据2x-3求代数式的值,,循环代入x=7,代数式的值,,再代入x=11,,再看x=19时,.该程序需要运行4次才停止.
(2)根据一次运算就停止,列不等式,解不等式即可.
(3)根据该程序只运行1次结果小于23,2次结果大于23就停,解不等式①得x≤13,解不等式②得x>8,不等式的解集:.
(1)
解:,
,
,
.
若,该程序需要运行4次才停止.
故答案为:4.
(2)
解:该程序只运行了1次就停止了
依题意得:,
解得:.
故答案为:.
(3)
依题意得:,
解不等式①得x≤13,
解不等式②得x>8,
不等式的解集:.
答:的取值范围为.
【点睛】
本题考查了程序与代数式的值,一元一次不等式的应用以及一元一次不等式组的应用,解题的关键是:(1)代入,找出程序运行的次数;(2)根据各数量之间的关系,正确列出一元一次不等式;(3)根据各数量之间的关系,正确列出一元一次不等式组.
3、 (1)14,62,26
(2)①②证明见解析
【解析】
【分析】
(1)根据例题写出对称积等式即可;
(2)①根据为整数且的和为三位数的十位数字,即可求得范围;
②根据规律列出等式,进而根据整式的乘法运算进行证明即可
(1)
41×154=451×14; 62×286=682×26
故答案为:14,62,26
(2)
设“对称积等式”这类等式左边两位数的十位数字为a,个位数字为b,
,,且为整数
②
证明:等式的左边等于
等式的右边等于
左边等于右边
原等式成立
【点睛】
本题考查了找规律,整式的乘法运算,不等式组的应用,找到规律是解题的关键.
4、,数轴见解析
【解析】
【分析】
先去分母,再去括号,移项、合并同类项,把的系数化为1.
【详解】
解:去分母得,,
去括号得,,
移项、合并同类项得,,
把的系数化为1得,.
在数轴上表示此不等式的解集如下:
【点睛】
本题考查了一元一次不等式的解法,熟练掌握解一元一次不等式的步骤是解答本题的关键.不等式的解集在数轴上表示时,空心圈表示不包含该点,实心点表示包含该点.
5、 (1)
(2)若售完这些商品,则至少购进200件甲商品商场可获得最大利润,获得的最大利润是13000元
【解析】
【分析】
(1)由题意得,整理即可得到函数关系式;
(2)由题意得,解得;由可知y随x的增大而减小,进而可求得购进的甲商品数,最大利润值.
(1)
解:由题意得
∴y与x的函数关系式为.
(2)
解:由题意得
解得
∵
∴y随x的增大而减小
∴当时,利润最大且
∴若售完这些商品,则至少购进200件甲商品商场可获得最大利润,获得的最大利润是13000元.
【点睛】
本题考查了一次函数的应用,一元一次不等式,一次函数的性质等知识.解题的关键在于根据题意列正确的等式或不等式.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如果a>b,那么下列不等式中正确的是( )
A.a-b>0 B.ac >bc C.c-a>c-b D.a+3<b-3
2、若关于的一元一次不等式组的解集为,且关于的方程的解为非负整数,则符合条件的所有整数的和为( )
A.2 B.7 C.11 D.10
3、已知,那么下列各式中,不一定成立的是( )
A. B. C. D.
4、若,则下列式子一定成立的是( )
A. B. C. D.
5、若点在第一象限,则a的取值范围是( )
A. B. C. D.无解
6、某天,孟孟与欢欢在讨论攀攀的年龄,欢欢说:“攀攀至多3岁.”而孟孟说:“攀攀的年龄一定大于1岁.”则攀攀年龄的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7、下列说法中不正确的个数有( )
①有理数的倒数是
②绝对值相等的两个数互为相反数
③绝对值既是它本身也是它的相反数的数只有0
④几个有理数相乘,若有奇数个负因数,则乘积为负数
⑤若,则
A.1个 B.2个 C.3个 D.4个
8、如图,直线y=kx+b与x轴的交点的坐标是(﹣3,0),那么关于x的不等式kx+b>0的解集是( )
A.x>﹣3 B.x<﹣3 C.x>0 D.x<0
9、如果不等式组的解集是,那么a的值可能是( )
A.-2 B.0 C.-0.7 D.
10、将不等式的解集表示在数轴上,正确的是( )
A. B.
C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、像这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个__________.
2、我们把几个一元一次不等式解集的__________,叫作由它们所组成的一元一次不等式组的解集.
3、如图,直线y=kx+b交坐标轴于A,B两点,则关于x的不等式kx+b<0的解集是_____.
4、不等式的最大整数解是_______.
5、若实数满足,则的取值范围为___________.
三、解答题(5小题,每小题10分,共计50分)
1、说出下列不等式变形的依据:
(1)由x-1>2,得x>3;
(2)由-2x>-4,得x<2;
(3)由-x<-1,得x>2;
(4)由3x<x,得2x<0.
2、在近几年的两会中,有多位委员不断提出应在中小学开展编程教育,2019年3月教育部公布的《2019年教育信息化和网络安全工作要点》中也提出将推广编程教育.某学校的编程课上,一位同学设计了一个运算程序,如图所示.按上述程序进行运算,程序运行到“判断结果是否大于23”为一次运行.
(1)若,直接写出该程序需要运行 次才停止;
(2)若该程序只运行了1次就停止了,则的取值范围是 .
(3)若该程序只运行了2次就停止了,求的取值范围.
3、仔细阅读下面例题,解答问题:
观察下列各计算题:
26×682=286×62
34×473=374×43
52×275=572×25
15×561=165×51
……
以上每个等式都非常巧妙,左边是一个两位数乘以三位数,等式两边的数字之间具有特殊性,一边的数字也有特殊性,且数字关于等号成对称分布,我们把满足这种条件的等式称为“对称积等式”.
(1)解决问题:填空,使下列各式成为“对称积等式”:41×154= ×14; ×286=682×
(2)解决问题:设“对称积等式”这类等式左边两位数的十位数字为a,个位数字为b,
①写出a+b的取值范围;
②请用含a、b的代数式写出表示“对称积等式”的式子,并证明你的结论.
4、解不等式:,并把它的解集在数轴上表示出来.
5、某商场同时购进甲乙两种商品共300件,其进价和售价如下表,设购进甲种商品x件,销售完300件商品的总利润为y元.
商品名称 甲 乙
进价(元/件) 50 70
售价(元/件) 90 120
(1)求y与x的函数关系式.
(2)该商品计划最多投入17000元用于购买这两种商品,若售完这些商品,则至少购进多少件甲商品商场可获得最大利润,获得的最大利润是多少元?
-参考答案-
一、单选题
1、A
【解析】
【分析】
在不等式的两边都加上或减去同一个数或整式,不等号的方向不变,在不等式的两边都乘以或除以同一个正数,不等号的方向不变,在不等式的两边都乘以或除以同一个负数,不等号的方向改变,根据不等式的基本性质逐一分析即可.
【详解】
解: a>b,
故A符合题意;
a>b,
当时, 故B不符合题意;
a>b,
故C不符合题意;
a>b,
故D不符合题意;
故选A
【点睛】
本题考查的是不等式的基本性质,掌握“不等式的基本性质”是解本题的关键.
2、B
【解析】
【分析】
先解关于的一元一次不等式组,再根据其解集是,得小于5;再解方程,根据其有非负整数解,得出的值,再求积即可.
【详解】
解:由,得:,
由,得:,
不等式组的解集为,
,
解得;
解关于的方程得:,
方程的解为非负整数,
或3或6或9,
解得或2或3.5或5,
所以符合条件的所有整数的和,
故选:B.
【点睛】
此题考查了解一元一次不等式组及一元一次方程的解,熟练掌握各自的解法是解本题的关键.
3、A
【解析】
【分析】
根据不等式的性质1不等式不等式两边同时加或减去同一个数或整式,不等号方向不变,基本性质2:不等式两边同时乘以(或除以)同一个大于0的整数,不等号方向不变 基本性质3:不等式两边同时乘以(或除以)同一个小于0的整数,不等号方向改变,根据不等式性质对各选项进行一一分析判断即可.
【详解】
解:.,不妨设,
则,
选项符合题意;
B.,
,
选项B不符合题意;
C.,
,
,
选项C不符合题意;
D.,
,
,
选项D不符合题意;
故选:A.
【点睛】
本题考查不等式性质,掌握不等式性质是解题关键.
4、B
【解析】
【分析】
根据不等式的性质依次分析判断.
【详解】
解:∵,∴a+1>b+1,故选项A不符合题意;
∵,∴,故选项B符合题意;
∵,∴-2a<-2b,故选项C不符合题意;
∵,∴,故选项D不符合题意;
故选:B.
【点睛】
此题考查了不等式的性质:不等式两边同时加上或减去同一个整式,不等号方向不变;不等式两边同时乘或除以同一个不为0的整正数,不等号方向不变;不等式两边同时乘或除以同一个不为0的负数,不等号方向改变.
5、B
【解析】
【分析】
由第一象限内的点的横纵坐标都为正数,可列不等式组,再解不等式组即可得到答案.
【详解】
解: 点在第一象限,
由①得:
由②得:
故选B
【点睛】
本题考查的是根据点所在的象限求解字母的取值范围,掌握坐标系内点的坐标特点是解本题的关键.
6、C
【解析】
【分析】
由至多得到小于等于,结合大于得到答案.
【详解】
解:由题意得,攀攀的年龄大于1且小于等于3,
故选:C.
【点睛】
此题考查了在数轴上表示不等式的解集,正确掌握大于、大于等于、小于等于的不同表示方法是解题的关键.
7、B
【解析】
【分析】
由倒数的定义可判断①,由绝对值的含义可判断②③,由有理数的乘法中积的符号确定方法可判断④,由不等式的基本性质可判断⑤,从而可得答案.
【详解】
解:因为 所以有理数的倒数是,故①正确;不符合题意
绝对值相等的两个数互为相反数或者相等,故②不正确;符合题意;
绝对值既是它本身也是它的相反数的数只有0,故③正确;不符合题意;
几个不为零有理数相乘,若有奇数个负因数,则乘积为负数,若其中一个因数为0,则结果为0,故④不正确;符合题意;
若,则,故⑤正确;不符合题意;
所以②④符合题意
故选: B.
【点睛】
本题考查的是倒数的含义,绝对值的含义,有理数乘法中积的符号确定,不等式的性质,掌握以上基础知识是解本题的关键.
8、A
【解析】
【分析】
根据图象直接解答即可.
【详解】
∵直线y=kx+b与x轴交点坐标为(﹣3,0),
∴由图象可知,当x>﹣3时,y>0,
∴不等式kx+b>0的解集是x>﹣3.
故选:A.
【点睛】
此题考查了一次函数图象与不等式的关系,不等式的解集即为一次函数的函数值大于零、等于零或小于零,正确理解二者之间的关系是解题的关键.
9、A
【解析】
【分析】
根究不等式组解集的确定原则,判定a≤-1,比较大小后,确定即可.
【详解】
∵不等式组的解集是,
∴a≤-1,
只有-2满足条件,
故选A.
【点睛】
本题考查了不等式组解集,正确理解不等式组解集的确定原则是解题的关键.
10、D
【解析】
【分析】
先求出不等式的解集,然后画出数轴,并在数轴上表示出不等式的解集.
【详解】
解:,
解得:,
表示在数轴上,如图所示:
.
故选:D.
【点睛】
本题考查了一元一次不等式的解法,熟练掌握解一元一次不等式的步骤是解答本题的关键.不等式的解集在数轴上表示时,空心圈表示不包含该点,实心点表示包含该点.
二、填空题
1、一元一次不等式组
【解析】
略
2、公共部分
【解析】
略
3、x<-2
【解析】
【分析】
根据图象,找出在x轴下方的函数图象所对应的自变量的取值即可得答案.
【详解】
∵点A坐标为(-2,0),
∴关于x的不等式kx+b<0的解集是x<-2,
故答案为:x<-2
【点睛】
本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合;熟练掌握函数图象法是解题关键.
4、2
【解析】
【分析】
首先根据不等式求解不等式,再根据不等式的解集写出最大的整数解.
【详解】
解:移项,得:,
合并同类项,得:,
系数化成1得:,
则最大整数解是:2.
故答案是:2.
【点睛】
本题主要考查不等式的整数解,关键在于求解不等式.
5、
【解析】
【分析】
先根据已知等式可得,从而可得,再根据绝对值的非负性、偶次方的非负性求出的取值范围,由此即可得出答案.
【详解】
解:由得:,
则,
,
,解得,
又,
,
,
即的取值范围为,
故答案为:.
【点睛】
本题考查了绝对值的非负性、偶次方的非负性、一元一次不等式组的应用,熟练掌握绝对值和偶次方的非负性是解题关键.
三、解答题
1、 (1)见解析
(2)见解析
(3)见解析
(4)见解析
【解析】
【分析】
(1)根据等式两边加上(或减去)同一个数,不等号方向不变求解;
(2)根据不等式两边乘以(或除以)同一个负数,不等号方向改变求解;
(3)根据不等式两边乘以(或除以)同一个负数,不等号方向改变求解;
(4)根据等式两边加上(或减去)同一个含有字母的式子,不等号方向不变求解.
(1)
解:由x-1>2,得x>3,不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;
(2)
解:由-2x>-4,得x<2,不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;
(3)
解:由-x<-1,得x>2,不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;
(4)
解:由3x<x,得2x<0,不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.
【点睛】
本题主要考查了不等式的性质,正确掌握不等式的性质是解题关键.
2、 (1)4
(2)
(3)
【解析】
【分析】
(1)当时,根据2x-3求代数式的值,,循环代入x=7,代数式的值,,再代入x=11,,再看x=19时,.该程序需要运行4次才停止.
(2)根据一次运算就停止,列不等式,解不等式即可.
(3)根据该程序只运行1次结果小于23,2次结果大于23就停,解不等式①得x≤13,解不等式②得x>8,不等式的解集:.
(1)
解:,
,
,
.
若,该程序需要运行4次才停止.
故答案为:4.
(2)
解:该程序只运行了1次就停止了
依题意得:,
解得:.
故答案为:.
(3)
依题意得:,
解不等式①得x≤13,
解不等式②得x>8,
不等式的解集:.
答:的取值范围为.
【点睛】
本题考查了程序与代数式的值,一元一次不等式的应用以及一元一次不等式组的应用,解题的关键是:(1)代入,找出程序运行的次数;(2)根据各数量之间的关系,正确列出一元一次不等式;(3)根据各数量之间的关系,正确列出一元一次不等式组.
3、 (1)14,62,26
(2)①②证明见解析
【解析】
【分析】
(1)根据例题写出对称积等式即可;
(2)①根据为整数且的和为三位数的十位数字,即可求得范围;
②根据规律列出等式,进而根据整式的乘法运算进行证明即可
(1)
41×154=451×14; 62×286=682×26
故答案为:14,62,26
(2)
设“对称积等式”这类等式左边两位数的十位数字为a,个位数字为b,
,,且为整数
②
证明:等式的左边等于
等式的右边等于
左边等于右边
原等式成立
【点睛】
本题考查了找规律,整式的乘法运算,不等式组的应用,找到规律是解题的关键.
4、,数轴见解析
【解析】
【分析】
先去分母,再去括号,移项、合并同类项,把的系数化为1.
【详解】
解:去分母得,,
去括号得,,
移项、合并同类项得,,
把的系数化为1得,.
在数轴上表示此不等式的解集如下:
【点睛】
本题考查了一元一次不等式的解法,熟练掌握解一元一次不等式的步骤是解答本题的关键.不等式的解集在数轴上表示时,空心圈表示不包含该点,实心点表示包含该点.
5、 (1)
(2)若售完这些商品,则至少购进200件甲商品商场可获得最大利润,获得的最大利润是13000元
【解析】
【分析】
(1)由题意得,整理即可得到函数关系式;
(2)由题意得,解得;由可知y随x的增大而减小,进而可求得购进的甲商品数,最大利润值.
(1)
解:由题意得
∴y与x的函数关系式为.
(2)
解:由题意得
解得
∵
∴y随x的增大而减小
∴当时,利润最大且
∴若售完这些商品,则至少购进200件甲商品商场可获得最大利润,获得的最大利润是13000元.
【点睛】
本题考查了一次函数的应用,一元一次不等式,一次函数的性质等知识.解题的关键在于根据题意列正确的等式或不等式.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
