初中数学苏科版八年级下册9.4 矩形、菱形、正方形完整版(含解析)
文档属性
| 名称 | 初中数学苏科版八年级下册9.4 矩形、菱形、正方形完整版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 16:01:54 | ||
图片预览



文档简介
矩形、菱形、正方形(完整)——1、矩形
知识点1:矩形的定义
有一个角是直角的平行四边形叫做矩形.
注意:矩形定义的两个要素:①是平行四边形;
②有一个角是直角.即矩形首先是一个平行四边形,然后增加一个角是直角这个特殊条件.
例1:矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为
A.12 B.14 C.16 D.18
知识点2:矩形的性质
矩形的性质包括四个方面:1.矩形具有平行四边形的所有性质;
2.矩形的对角线相等;
3.矩形的四个角都是直角;
4.矩形是轴对称图形,它有两条对称轴.
注意:(1)矩形是特殊的平行四边形,因而也是中心对称图形.过中心的任意直线可将矩形分成完全全等的两部分.
(2)矩形也是轴对称图形,有两条对称轴(分别通过对边中点的直线).对称轴的交点就是对角线的交点(即对称中心).
(3)矩形是特殊的平行四边形,矩形具有平行四边形的所有性质,从而矩形的性质可以归结为从三个方面看:从边看,矩形对边平行且相等;从角看,矩形四个角都是直角;从对角线看,矩形的对角线互相平分且相等.
例2:如图,在矩形中,,,点为边上任意一点,过点作,,垂足分别为、,则 .
例3:如图,一张矩形纸片,,.点在这张矩形纸片的边上,将纸片折叠,使落在射线上,折痕为,点,分别落在点,处,
(1)若,则的度数为 ;
(2)若,求的长.
知识点3:矩形的判定
矩形的判定有三种方法:
1.定义:有一个角是直角的平行四边形叫做矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
注意:在平行四边形的前提下,加上“一个角是直角”或“对角线相等”都能判定平行四边形是矩形.
例1:在平行四边形中添加下列条件,不能判定四边形是矩形的是
A. B. C. D.
例2 :已知:如图,在中,,是的中线,为的外角的平分线,,交于点.求证:四边形是矩形.
矩形、菱形、正方形(完整)—2、菱形
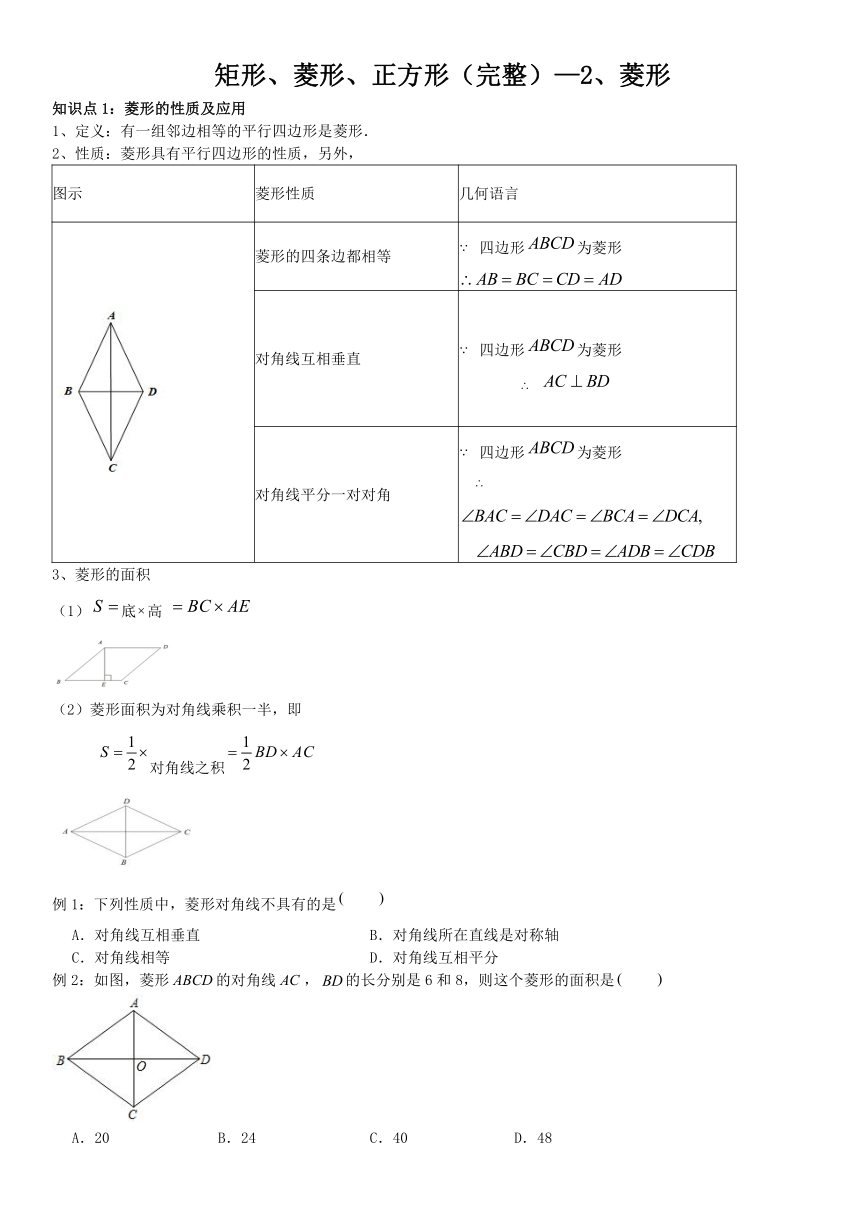
知识点1:菱形的性质及应用
1、定义:有一组邻边相等的平行四边形是菱形.
2、性质:菱形具有平行四边形的性质,另外,
图示 菱形性质 几何语言
菱形的四条边都相等 四边形为菱形
对角线互相垂直 四边形为菱形
对角线平分一对对角 四边形为菱形
3、菱形的面积
(1)底高
(2)菱形面积为对角线乘积一半,即
对角线之积
例1:下列性质中,菱形对角线不具有的是
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
例2:如图,菱形的对角线,的长分别是6和8,则这个菱形的面积是
A.20 B.24 C.40 D.48
例3:如图,四边形是菱形,对角线,相交于点,且.
(1)菱形的周长为 ;
(2)若,求的长.
知识点2:菱形的判定
图示 判定定理 几何语言
有一组邻边相等的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
对角线互相垂直的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
四边相等的四边形是菱形 平行四边形为菱形
注意:运用前两种方法时,必须先识别四边形是平行四边形,然后再从有一组邻边相等或对角线互相垂直这两个方面来探讨;最后一种判定方法时任意四边形,只要满足了四条边都相等就能证明时菱形.
例1:如图,在中,对角线、相交于点,下列条件中,不能判断这个平行四边形是菱形的是
A. B. C. D.
例2 :在中,点、分别在、上,且.
(1)求证:;
(2)若,求证:四边形为菱形.
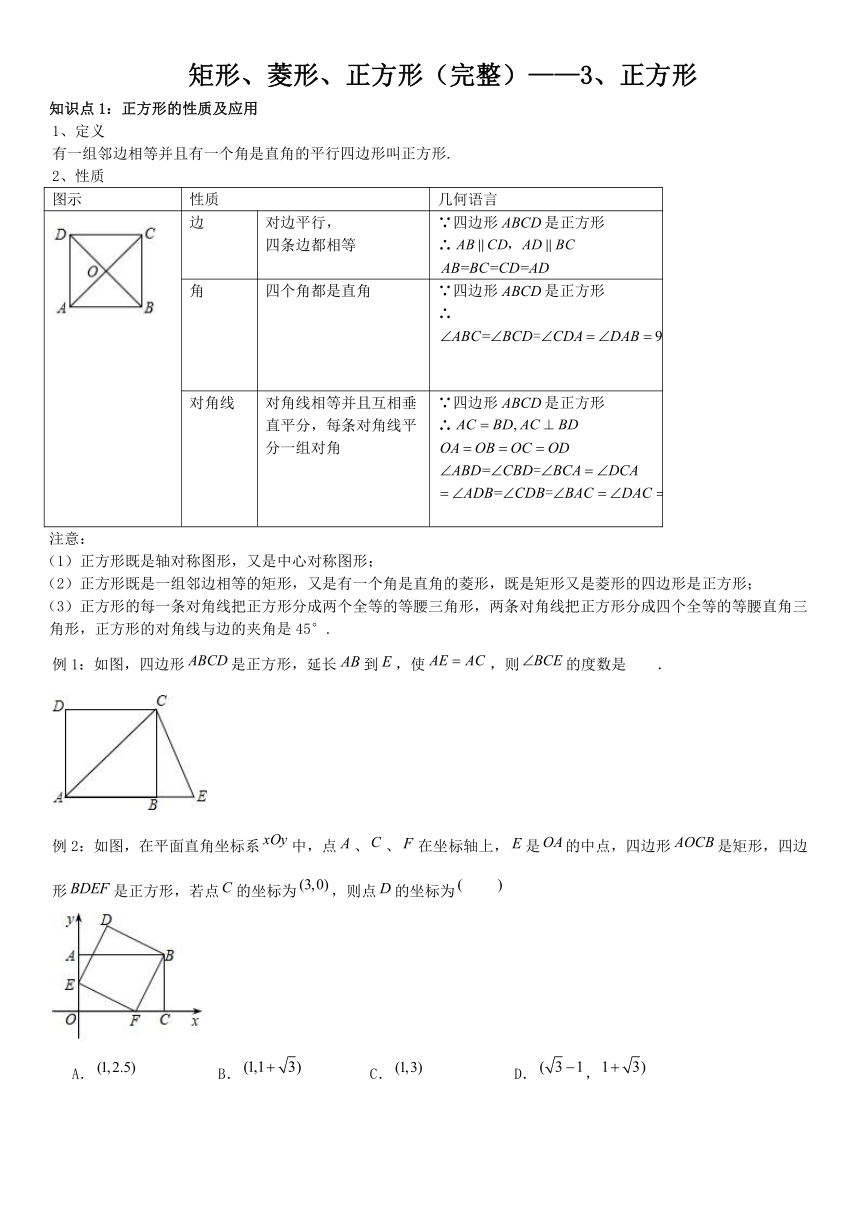
矩形、菱形、正方形(完整)——3、正方形
知识点1:正方形的性质及应用
1、定义
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2、性质
图示 性质 几何语言
边 对边平行, 四条边都相等 ∵四边形是正方形 ∴
角 四个角都是直角 ∵四边形是正方形 ∴
对角线 对角线相等并且互相垂直平分,每条对角线平分一组对角 ∵四边形是正方形 ∴
注意:
(1)正方形既是轴对称图形,又是中心对称图形;
(2)正方形既是一组邻边相等的矩形,又是有一个角是直角的菱形,既是矩形又是菱形的四边形是正方形;
(3)正方形的每一条对角线把正方形分成两个全等的等腰三角形,两条对角线把正方形分成四个全等的等腰直角三角形,正方形的对角线与边的夹角是45°.
例1:如图,四边形是正方形,延长到,使,则的度数是 .
例2:如图,在平面直角坐标系中,点、、在坐标轴上,是的中点,四边形是矩形,四边形是正方形,若点的坐标为,则点的坐标为
A. B. C. D.,
知识点2:正方形的判定
正方形的判定
图示 判定定理 几何语言
有一组邻边相等的矩形是正方形 ∵四边形是矩形, ∴四边形是正方形
有一个角是直角的菱形是正方形 ∵四边形是菱形, ∴四边形是正方形
补充:判定四边形是正方形
①对角线互相垂直平分且相等的四边形是正方形;
②对角线互相垂直且相等的平行四边形是正方形;
③对角线相等的菱形是正方形;
④对角线互相垂直的矩形是正方形;
⑤既是菱形又是矩形的四边形是正方形.
例1:小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①,②,③,④中任选两个作为补充条件,使为正方形.现有下列四种选法,你认为其中错误的是
A.②③ B.①③ C.①② D.③④
例2 :如图,在中,对角线、交于点,是延长线上的点,且是等边三角形.
(1)求证:四边形是菱形.
(2)若,求证:四边形是正方形.
矩形练习:
1、检查一个门框是否为矩形,下列方法中正确的是
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量两条对角线,是否互相垂直
D.测量门框的三个角,是否都是直角
2、如图,在中,点在上,,,下列四个判断中不正确的是
A.四边形是平行四边形
B.若,则四边形是矩形
C.若且,则四边形是菱形
D.若平分,则四边形是矩形
3、如图,在中,再添加一个条件 (写出一个即可),是矩形(图形中不再添加辅助线)
4、如图,矩形中,对角线的垂直平分线分别交,于点,,若,,则的长为
A. B. C. D.
5、如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是
A.1 B. C.2 D.
6、如图,在矩形中对角线与相交于点,,垂足为点,,,则的长为
A. B.4 C.6 D.8
7、若矩形两条对角线的夹角是,且较短的边长为3,则这个矩形的面积为 .
8.如图,在矩形中,的平分线交与点,,,则 .
9.如图,矩形的对角线与交于点,过点作的垂线分别交、于、两点,若,,则的长度为 .
10.如图,矩形中,点、分别在、上,,交于点.若,,则图中两块阴影部分的面积之和为 .
11、如图,在矩形中,点在上,平分.
(1)是否为等腰三角形?为什么?
(2)已知,,求的长.
12、如图,在四边形中,,,,,,点从点出发沿边以每秒的速度向点运动, 秒后四边形是矩形.
13、如图,在ABCD中,对角线AC,BD交于点O,且.
求证:ABCD是矩形;
点E在BA延长线上,且,连接DE,求证:.
14、如图,在平行四边形ABCD中,于点E,延长BC至F点使,连接AF,DE,DF.
求证:四边形AEFD是矩形;
若,,,求AE的长。
15、如图,四边形ABCD中,对角线AC、BD相交于点O,,,且.
求证:四边形ABCD是矩形;
,若::2,则的度数是多少?
16、已知:如图,在四边形中,点在边的延长线上,平分,平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
17、如图所示,在中,是上一点,是的中点,过点作交的延长线于点,且,连接.
(1)猜想与有什么数量关系,并说明理由;
(2)当满足什么条件时,四边形是矩形?并说明理由.
菱形练习:
1、下列性质中,菱形具有而矩形不一定具有的是
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边互相垂直
2、如图,四边形是菱形,,,于,则等于
A. B.4 C. D.5
3、如图,平面直角坐标系中,菱形的顶点,,顶点在轴正半轴上,则点的坐标为
A. B. C. D.
4、如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为( )
A . 仅甲正确 B . 仅乙正确
C . 甲、 乙均正确 D . 甲、 乙均错误
5、如图将菱形竖直位置的对角线向右平移,水平位置的对角线向上平移,平移后菱形被分成四块,最大一块与最小一块的面积和记为,其余两块的面积和记为,则与的差是
A. B. C. D.
6、如图,、、、分别是、、、的中点,且,下列结论:①;②四边形是矩形;③平分;④;⑤四边形周长等于.其中正确的个数是
A.1 B.2 C.3 D.4
7、如图,菱形的对角线、相交于点,、分别为边、的中点,连接.若,,则菱形的周长为 .
8、如图,四边形是菱形,对角线,,于点,则的长为 .
9、已知三角形的三条中位线的长分别为、、,则这个三角形的周长是 .
10、矩形的对角线与相交于点,,,分别是,的中点,则的长度为 .
11、已知:如图,在正方形中,点、在对角线上,且,
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
12、如图,矩形的对角线、相交于点,,.
(1)求证:四边形为菱形;
(2)垂直平分线线段于点,,求的长.
13、如图,在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
求证:≌;
求证:四边形ADCF是菱形;
若,,求菱形ADCF的面积.
正方形练习:
1、如图,正方形中,在延长线上取一点,使,连接,则的度数为
A. B. C. D.
2、如图,已知正方形的边长为3,、分别是、边上的点,且,若,则的长为 .
3、如图,在边长为的正方形中,以为边在正方形内作等边,连接并延长交于点,连接.请从,两题中任选一题作答:
.的度数等于 .
.线段的长是 .
4、下列说法正确的是
A.正方形的每一条对角线平分一组对角
B.矩形的对角线互相垂直
C.菱形的四个内角都是直角
D.平行四边形是轴对称图形
5、如图,正方形中,点是对角线上一点,连接,边作交边于于点,且点不与点,重合,作,,垂足分别为点和.
(1)求证:;
(2)求证:.
6、如图,正方形中,是边上一点,是延长线上一点,且,若四边形的面积是,则长是 .
7、下列命题,不正确的是
A.对角线相等且垂直的四边形是正方形
B.有一个角是直角的菱形是正方形
C.顺次连接菱形各边中点所得的四边形是矩形
D.有一个角是的等腰三角形是等边三角形
8、如图,四边形是平行四边形,与相交于点,,添加一个条件: ,可使它成为正方形.
9、已知矩形,给出三个关系式:①;②;③,如果选择关系式 作为条件(写出一个即可),那么可以判定矩形为正方形,理由是 .
10、如图,在矩形中,点在边上,连结,将矩形沿折叠,点的对称点落在边上,连结.求证:四边形是正方形.
11、下列说法不能判断是正方形的是
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
12、已知平行四边形,对角线、相交于点,且,延长至点,使,连接.
(1)当时,求证:;
(2)当时,求证:四边形是正方形.
13、如图,在中,,的垂直平分线交于点,交于点,且,添加一个条件,仍不能证明四边形为正方形的是
A. B. C. D.
14、如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作,求证:四边形OCED是正方形.
矩形、菱形、正方形(完整)——1、矩形
知识点1:矩形的定义
有一个角是直角的平行四边形叫做矩形.
注意:矩形定义的两个要素:①是平行四边形;
②有一个角是直角.即矩形首先是一个平行四边形,然后增加一个角是直角这个特殊条件.
例1:矩形的对角线、相交于点,,,则的周长为
A.12 B.14 C.16 D.18
【解答】解:四边形是矩形,
,,,
,
,
,
是等边三角形,
,
的周长;
故选:.
知识点2:矩形的性质
矩形的性质包括四个方面:1.矩形具有平行四边形的所有性质;
2.矩形的对角线相等;
3.矩形的四个角都是直角;
4.矩形是轴对称图形,它有两条对称轴.
注意:(1)矩形是特殊的平行四边形,因而也是中心对称图形.过中心的任意直线可将矩形分成完全全等的两部分.
(2)矩形也是轴对称图形,有两条对称轴(分别通过对边中点的直线).对称轴的交点就是对角线的交点(即对称中心).
(3)矩形是特殊的平行四边形,矩形具有平行四边形的所有性质,从而矩形的性质可以归结为从三个方面看:从边看,矩形对边平行且相等;从角看,矩形四个角都是直角;从对角线看,矩形的对角线互相平分且相等.
例2:如图,在矩形中,,,点为边上任意一点,过点作,,垂足分别为、,则 .
【解答】解:连接,如图:
四边形是矩形,
,,,,
,,
,,,
,
;
故答案为:.
例3:如图,一张矩形纸片,,.点在这张矩形纸片的边上,将纸片折叠,使落在射线上,折痕为,点,分别落在点,处,
(1)若,则的度数为 ;
(2)若,求的长.
【解答】解:(1)四边形是矩形,
,
,,
由折叠的性质得:,
;
故答案为:70;
(2),,
,
四边形是矩形,
,,
,
由翻折不变性可知,,
,
,
,,
在中,由勾股定理得:,
,
由翻折不变性可知,,
.
知识点3:矩形的判定
矩形的判定有三种方法:
1.定义:有一个角是直角的平行四边形叫做矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
注意:在平行四边形的前提下,加上“一个角是直角”或“对角线相等”都能判定平行四边形是矩形.
例1:在平行四边形中添加下列条件,不能判定四边形是矩形的是
A. B. C. D.
【解答】解:
、四边形是平行四边形,,
四边形是矩形,故本选项不符合题意;
、根据四边形是平行四边形和不能推出四边形是矩形,故本选项符合题意;
、四边形是平行四边形,,
四边形是矩形,故本选项不符合题意;
、,
,
四边形是平行四边形,
,,
,
四边形是矩形,故本选项不符合题意;
故选:.
例2 :已知:如图,在中,,是的中线,为的外角的平分线,,交于点.求证:四边形是矩形.
【解答】证明:在中,,是边的中线,
,,
,
为的外角的平分线,
,
,
,
,
四边形为矩形.
矩形、菱形、正方形(完整)——2菱形
知识点1:菱形的性质及应用
1、定义:有一组邻边相等的平行四边形是菱形.
2、性质:菱形具有平行四边形的性质,另外,
图示 菱形性质 几何语言
菱形的四条边都相等 四边形为菱形
对角线互相垂直 四边形为菱形
对角线平分一对对角 四边形为菱形
3、菱形的面积
(1)底高
(2)菱形面积为对角线乘积一半,即
对角线之积
例1:下列性质中,菱形对角线不具有的是
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
【解答】解:菱形对角线具有的性质有:对角线互相垂直,对角线互相平分,
对角线所在直线是对称轴.
故,,正确,错误.
故选:.
例2:如图,菱形的对角线,的长分别是6和8,则这个菱形的面积是
A.20 B.24 C.40 D.48
【解答】解:菱形的对角线,的长分别是6和8,
菱形的面积.
故选:.
例3:如图,四边形是菱形,对角线,相交于点,且.
(1)菱形的周长为 ;
(2)若,求的长.
【解答】解:(1)四边形是菱形,,
菱形的周长为:8;
故答案为8.
(2)四边形是菱形,,,
,,
,
.
知识点2:菱形的判定
图示 判定定理 几何语言
有一组邻边相等的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
对角线互相垂直的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
四边相等的四边形是菱形 平行四边形为菱形
注意:运用前两种方法时,必须先识别四边形是平行四边形,然后再从有一组邻边相等或对角线互相垂直这两个方面来探讨;最后一种判定方法时任意四边形,只要满足了四条边都相等就能证明时菱形.
例1:如图,在中,对角线、相交于点,下列条件中,不能判断这个平行四边形是菱形的是
A. B. C. D.
【解答】解:、邻边相等的平行四边形是菱形,故选项不符合题意;
、对角线平分对角的平行四边形是菱形,故选项不符合题意;
、由不一定能够判断这个平行四边形是菱形,故选项符合题意;
、对角线互相垂直平分的平行四边形是菱形,故选项不符合题意.
故选:.
例2 :在中,点、分别在、上,且.
(1)求证:;
(2)若,求证:四边形为菱形.
【解答】证明:(1)四边形是平行四边形,
,,
在和中,
,
;
(2)四边形是平行四边形,
,,
,
,
四边形是平行四边形,
又,
四边形为菱形.
矩形、菱形、正方形(完整)——3、正方形
知识点1:正方形的性质及应用
1、定义
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2、性质
图示 性质 几何语言
边 对边平行, 四条边都相等 ∵四边形是正方形 ∴
角 四个角都是直角 ∵四边形是正方形 ∴
对角线 对角线相等并且互相垂直平分,每条对角线平分一组对角 ∵四边形是正方形 ∴
注意:
(1)正方形既是轴对称图形,又是中心对称图形;
(2)正方形既是一组邻边相等的矩形,又是有一个角是直角的菱形,既是矩形又是菱形的四边形是正方形;
(3)正方形的每一条对角线把正方形分成两个全等的等腰三角形,两条对角线把正方形分成四个全等的等腰直角三角形,正方形的对角线与边的夹角是45°.
例1:如图,四边形是正方形,延长到,使,则的度数是 .
【解答】解:四边形是正方形,
,
,
,
.
故答案为:.
例2:如图,在平面直角坐标系中,点、、在坐标轴上,是的中点,四边形是矩形,四边形是正方形,若点的坐标为,则点的坐标为
A. B. C. D.,
【解答】解:过作轴于,
四边形是矩形,四边形是正方形,
,,
,
,
,
,
,,
,
是的中点,
,
点的坐标为,
,
,,
同理,
,,
,
点的坐标为,
故选:.
知识点2:正方形的判定
正方形的判定
图示 判定定理 几何语言
有一组邻边相等的矩形是正方形 ∵四边形是矩形, ∴四边形是正方形
有一个角是直角的菱形是正方形 ∵四边形是菱形, ∴四边形是正方形
补充:判定四边形是正方形
①对角线互相垂直平分且相等的四边形是正方形;
②对角线互相垂直且相等的平行四边形是正方形;
③对角线相等的菱形是正方形;
④对角线互相垂直的矩形是正方形;
⑤既是菱形又是矩形的四边形是正方形.
例1:小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①,②,③,④中任选两个作为补充条件,使为正方形.现有下列四种选法,你认为其中错误的是
A.②③ B.①③ C.①② D.③④
【解答】解:、四边形是平行四边形,
当②时,平行四边形是矩形,
当时,这是矩形的性质,无法得出四边形是正方形,故此选项错误,符合题意;
、四边形是平行四边形,
当①时,平行四边形是菱形,
当③时,菱形是正方形,故此选项正确,不合题意;
、四边形是平行四边形,
当①时,平行四边形是菱形,
当②时,菱形是正方形,故此选项正确,不合题意;
、四边形是平行四边形,
当③时,平行四边形是矩形,
当④时,矩形是正方形,故此选项正确,不合题意.
故选:.
例2 :如图,在中,对角线、交于点,是延长线上的点,且是等边三角形.
(1)求证:四边形是菱形.
(2)若,求证:四边形是正方形.
【解答】证明:(1),
,
是等边三角形,
(三线合一)
即,
是菱形;
(2)是等边三角形,
由(1)知,,
,是直角三角形
,
,
,
,
是菱形,
,
菱形是正方形.
矩形练习:
1、检查一个门框是否为矩形,下列方法中正确的是
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量两条对角线,是否互相垂直
D.测量门框的三个角,是否都是直角
【解析】对角线相等的平行四边形是矩形,
故不符合题意;
对角线互相平分的四边形是平行四边形,
故不符合题意,
两条对角线互相垂直的四边形不一定是矩形,
故不符合题意;
三个角都是直角的四边形是矩形,
故符合题意;
故选:.
2、如图,在中,点在上,,,下列四个判断中不正确的是
A.四边形是平行四边形
B.若,则四边形是矩形
C.若且,则四边形是菱形
D.若平分,则四边形是矩形
【解析】因为,,所以四边形是平行四边形.故正确.
,四边形是平行四边形,所以四边形是矩形.故正确.
若且,则四边形是菱形,故正确;
因为平分,所以,又因为四边形是平行四边形,所以是菱形.故错误.
故选:.
3、如图,在中,再添加一个条件 (写出一个即可),是矩形(图形中不再添加辅助线)
【解析】添加的条件是,
理由是:,四边形是平行四边形,
平行四边形是矩形,
故答案为:
4、如图,矩形中,对角线的垂直平分线分别交,于点,,若,,则的长为
A. B. C. D.
【解析】如图,连接,设与交点为,
是的垂直平分线,
,,
四边形是矩形,
,,
,
在和中,
,
,
,
,,
,
,
故选:.
5、如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是
A.1 B. C.2 D.
【解析】连接,如图所示:
四边形是矩形,
,,,,
,
,
设,则,
在中,由勾股定理得:,
解得:,
即;
故选:.
6、如图,在矩形中对角线与相交于点,,垂足为点,,,则的长为
A. B.4 C.6 D.8
【解析】四边形是矩形,
,
, 故选:.
7、若矩形两条对角线的夹角是,且较短的边长为3,则这个矩形的面积为 .
【解答】解:如图所示:
四边形是矩形,
,,,,
,
又,
是等边三角形,
,
,
矩形的面积
故答案为:
8.如图,在矩形中,的平分线交与点,,,则 .
【解答】解:四边形是矩形,
,,,,
,
,
,
在中,.
故答案为.
9.如图,矩形的对角线与交于点,过点作的垂线分别交、于、两点,若,,则的长度为 .
【解答】解:四边形是矩形,
,
,
,
,,
,,
四边形是矩形,
,,
,
,
又中,,
,
,
故答案为:2.
10.如图,矩形中,点、分别在、上,,交于点.若,,则图中两块阴影部分的面积之和为 .
【解答】解:如图,过点作于,交于,
,,
,
,且,,
易证:四边形是矩形,四边形是矩形,四边形是矩形,四边形是矩形
,,,,,
,
两块阴影部分的面积之和为10 故答案为10
11、如图,在矩形中,点在上,平分.
(1)是否为等腰三角形?为什么?
(2)已知,,求的长.
【解答】解:(1)是等腰三角形,
理由是:四边形是矩形,
,
,
平分,
,
,
,
即是等腰三角形.
(2)四边形是矩形,
,
,
,
,
由勾股定理得:,
即.
12、、如图,在四边形中,,,,,,点从点出发沿边以每秒的速度向点运动, 秒后四边形是矩形.
【解析】当时,四边形是矩形,
此时:,,
在中,,
所以3秒后四边形是矩形,
故答案为:3
13、如图,在ABCD中,对角线AC,BD交于点O,且.
【解析】求证:ABCD是矩形;
点E在BA延长线上,且,连接DE,求证:.
证明:四边形ABCD是平行四边形,
,,
,
,
平行四边形ABCD是矩形;
四边形ABCD是平行四边形,
,,
又,
,
四边形DEAC是平行四边形,
.
14、如图,在平行四边形ABCD中,于点E,延长BC至F点使,连接AF,DE,DF.
求证:四边形AEFD是矩形;
若,,,求AE的长。
【解析】.证明:,
.
即 .
在 ABCD中,且,
且.
四边形AEFD是平行四边形.
,
.
四边形AEFD是矩形;
解:四边形AEFD是矩形,,
.
,,
.
.
,
的面积.
.
15、如图,四边形ABCD中,对角线AC、BD相交于点O,,,且.
求证:四边形ABCD是矩形;
,若::2,则的度数是多少?
【解析】证明:,
四边形ABCD是平行四边形,
,
,
,
四边形ABCD是矩形;
解:,::2,
,
,
,
四边形ABCD是矩形,
,
.
16、已知:如图,在四边形中,点在边的延长线上,平分,平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
【解析】证明:
(1)平分、平分,
,,
,
,,
,,
,,
;
(2)点为的中点,
,
又,
四边形是平行四边形,
平分、平分,
,
,
即,
四边形是矩形.
17、如图所示,在中,是上一点,是的中点,过点作交的延长线于点,且,连接.
(1)猜想与有什么数量关系,并说明理由;
(2)当满足什么条件时,四边形是矩形?并说明理由.
【解析】(1)猜想:,
证明:,
,
是的中点,
,
在和中,
,
,
,
,
;
(2)猜想:当是以为顶点的等腰三角形时,四边形是矩形;
证明:连接,
,,
四边形是平行四边形,
同理可得四边形是平行四边形,
,
是等腰三角形,即,
,
是矩形.
菱形练习:
1、下列性质中,菱形具有而矩形不一定具有的是
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边互相垂直
【解答】解:(A)对角线相等是矩形具有的性质,菱形不一定具有;
(B)对角线互相平分是菱形和矩形共有的性质;
(C)对角线互相垂直是菱形具有的性质,矩形不一定具有;
(D)邻边互相垂直是矩形具有的性质,菱形不一定具有.
故选:.
2、如图,四边形是菱形,,,于,则等于
A. B.4 C. D.5
【解答】解:四边形是菱形,
,,,
,
,
,
,
故选:.
3、如图,平面直角坐标系中,菱形的顶点,,顶点在轴正半轴上,则点的坐标为
A. B. C. D.
【解答】解:菱形的顶点,,
,,
,
点的坐标为
故选:.
4、如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为( )
A . 仅甲正确 B . 仅乙正确
C . 甲、 乙均正确 D . 甲、 乙均错误
【解答】解: 甲的作法正确;
四边形是平行四边形,
,
,
是的垂直平分线,
,
在和中,
,
,
,
又,
四边形是平行四边形,
,
四边形是菱形;
乙的作法正确;
,
,,
平分,平分,
,,
,,
,,
,且,
四边形是平行四边形,
,
平行四边形是菱形;
故选:C.
5、如图将菱形竖直位置的对角线向右平移,水平位置的对角线向上平移,平移后菱形被分成四块,最大一块与最小一块的面积和记为,其余两块的面积和记为,则与的差是
A. B. C. D.
【解答】解:如图,作关于的对称线段,作关于的对称线段,
由对称性可知,图中对应颜色的部分面积相等,
与的差,
,,
,
故选:.
6、如图,、、、分别是、、、的中点,且,下列结论:①;②四边形是矩形;③平分;④;⑤四边形周长等于.其中正确的个数是
A.1 B.2 C.3 D.4
【解答】解:、、、分别是、、、的中点,
,,,,
,
,,
四边形是菱形,
①,正确;
②四边形是矩形,错误;
③平分,正确;
④当,如图所示:,分别为,中点,
连接,延长交上一点,
,,
,故本小题错误;
⑤四边形周长等于,正确;
综上所述,①③⑤共3个正确;
故选:.
7、如图,菱形的对角线、相交于点,、分别为边、的中点,连接.若,,则菱形的周长为 .
【解答】解:、是和的中点,即是的中位线,
,
,,
在中,,
所以菱形的周长为8,
故答案为:8
8、如图,四边形是菱形,对角线,,于点,则的长为 .
【解答】解:四边形是菱形,
,,,
,
,
.
9、已知三角形的三条中位线的长分别为、、,则这个三角形的周长是 .
【解答】解:三角形的三条中位线的长分别是、、,
三角形的三条边分别是、、.
这个三角形的周长.
故答案是:42.
10、矩形的对角线与相交于点,,,分别是,的中点,则的长度为 .
【解答】解:四边形为矩形,
,
又因为矩形对角线的交点等分对角线,
,
又在中,,分别是,的中点,
为的中位线,
,
故答案为:1.
11、已知:如图,在正方形中,点、在对角线上,且,
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
【解答】(1)证明:正方形中,对角线,
,
.
,
.
四边形是菱形;
(2)解:在中,由勾股定理,得
,
,
,
四边形的面积
.
12、如图,矩形的对角线、相交于点,,.
(1)求证:四边形为菱形;
(2)垂直平分线线段于点,,求的长.
【解析】证明:(1),,
四边形是平行四边形,
矩形的对角线,相交于点,
,
四边形为菱形.
(2)过作,
矩形的对角线、相交于点,
,
垂直平分线线段于点,
,
是等边三角形,
,
,
,
,,
,
.
13、如图,在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
求证:≌;
求证:四边形ADCF是菱形;
若,,求菱形ADCF的面积.
解:证明:,
,
是AD的中点,AD是BC边上的中线,
,,
在和中,
,
≌;
证明:由知,≌,
则
,
.
,
四边形ADCF是平行四边形,
,D是BC的中点,E是AD的中点,
,
四边形ADCF是菱形;
正方形练习:
1、如图,正方形中,在延长线上取一点,使,连接,则的度数为
A. B. C. D.
【解答】解:四边形是正方形,
,
,
,
,
故选:.
2、如图,已知正方形的边长为3,、分别是、边上的点,且,若,则的长为 .
【解答】解:如图,将绕点按逆时针方向旋转得到.
绕点逆时针旋转得到,
,,,
,
点,点,点三点共线,
,
,
,
在和中,
,
;
设,
,,
,,
.
在中,由勾股定理得,
即,
解得:,
则的长为,
故答案为:.
3、如图,在边长为的正方形中,以为边在正方形内作等边,连接并延长交于点,连接.请从,两题中任选一题作答:
.的度数等于 .
.线段的长是 .
【解答】解:.△为等边三角形,
,,
四边形是正方形,
,,
,,
,
,
,
故答案为:;
.作,与交于点,如下图,则,
设,
,
,
,
,
,
,
,
,
解得,,
即,
故答案为:.
4、下列说法正确的是
A.正方形的每一条对角线平分一组对角
B.矩形的对角线互相垂直
C.菱形的四个内角都是直角
D.平行四边形是轴对称图形
【解答】解:.正方形的每一条对角线平分一组对角,故选项符合题意;
.矩形的对角线不一定互相垂直,故选项不符合题意;
.菱形的四个内角不一定都是直角,故选项不符合题意;
.平行四边形不一定是轴对称图形,故选项不符合题意;
故选:.
5、如图,正方形中,点是对角线上一点,连接,边作交边于于点,且点不与点,重合,作,,垂足分别为点和.
(1)求证:;
(2)求证:.
【解答】证明:(1)四边形为正方形,
平分,
又,,
.
(2),,,,
四边形为正方形,
,即.
,
,
.
,,
.
在和中,,
,
.
6、如图,正方形中,是边上一点,是延长线上一点,且,若四边形的面积是,则长是 .
【解答】解:四边形是正方形,
,,
在和中,
,
,
,
四边形的面积是,
正方形的面积是,
,
7、下列命题中,不正确的是
A.对角线相等且垂直的四边形是正方形
B.有一个角是直角的菱形是正方形
C.顺次连接菱形各边中点所得的四边形是矩形
D.有一个角是的等腰三角形是等边三角形
【解答】解:、对角线互相平分、相等且垂直的四边形是正方形,本选项说法不正确,符合题意;
、有一个角是直角的菱形是正方形,本选项说法正确,不符合题意;
、顺次连接菱形各边中点所得的四边形是矩形,本选项说法正确,不符合题意;
、有一个角是的等腰三角形是等边三角形,选项说法不正确,不符合题意;
故选:.
8、如图,四边形是平行四边形,与相交于点,,添加一个条件: ,可使它成为正方形.
【解答】解:因为四边形是平行四边形,,
所以是菱形,
如果,
那么四边形是正方形.
故答案为:.
9、已知矩形,给出三个关系式:①;②;③,如果选择关系式 作为条件(写出一个即可),那么可以判定矩形为正方形,理由是 .
【解答】解:四边形是矩形,,
矩形为正方形(对角线互相垂直的矩形是正方形),
故答案为:③,对角线互相垂直的矩形是正方形.
10、如图,在矩形中,点在边上,连结,将矩形沿折叠,点的对称点落在边上,连结.求证:四边形是正方形.
【解答】证明:四边形是矩形,
.
由折叠,得
.
四边形是矩形.
,
四边形是正方形.
11、下列说法不能判断是正方形的是
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
【解答】解:.对角线互相垂直且相等的平行四边形是正方形,故选项不符合题意;
.对角线互相垂直的矩形是正方形,故选项不符合题意;
.对角线相等的菱形是正方形,故选项不符合题意;
.对角线互相垂直平分的四边形是菱形,菱形不一定是正方形,故选项符合题意;
故选:.
12、已知平行四边形,对角线、相交于点,且,延长至点,使,连接.
(1)当时,求证:;
(2)当时,求证:四边形是正方形.
【解答】(1)证明:四边形是平行四边形,
又,
四边形是菱形.
.
又,
,
;
(2)证明:四边形是平行四边形,
,,
又,
,,
四边形是平行四边形.
,
平行四边形是矩形,
又,
,
矩形是正方形.
13、如图,在中,,的垂直平分线交于点,交于点,且,添加一个条件,仍不能证明四边形为正方形的是
A. B. C. D.
【解答】解:垂直平分,
,,
,
,
四边形是菱形;
当时,
,
则时,菱形是正方形.
,,
菱形是正方形.
故选项正确,但不符合题意;
当时,利用正方形的判定得出,菱形是正方形,故选项正确,但不符合题意;
当时,利用正方形的判定得出,菱形是正方形,故选项正确,但不符合题意;
当时,无法得出菱形是正方形,故选项错误,符合题意.
故选:.
14、如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作,求证:四边形OCED是正方形.
【解析】证明:,,
四边形OCED是平行四边形,
四边形ABCD是正方形,
,,
,
四边形OCED是正方形.
知识点1:矩形的定义
有一个角是直角的平行四边形叫做矩形.
注意:矩形定义的两个要素:①是平行四边形;
②有一个角是直角.即矩形首先是一个平行四边形,然后增加一个角是直角这个特殊条件.
例1:矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为
A.12 B.14 C.16 D.18
知识点2:矩形的性质
矩形的性质包括四个方面:1.矩形具有平行四边形的所有性质;
2.矩形的对角线相等;
3.矩形的四个角都是直角;
4.矩形是轴对称图形,它有两条对称轴.
注意:(1)矩形是特殊的平行四边形,因而也是中心对称图形.过中心的任意直线可将矩形分成完全全等的两部分.
(2)矩形也是轴对称图形,有两条对称轴(分别通过对边中点的直线).对称轴的交点就是对角线的交点(即对称中心).
(3)矩形是特殊的平行四边形,矩形具有平行四边形的所有性质,从而矩形的性质可以归结为从三个方面看:从边看,矩形对边平行且相等;从角看,矩形四个角都是直角;从对角线看,矩形的对角线互相平分且相等.
例2:如图,在矩形中,,,点为边上任意一点,过点作,,垂足分别为、,则 .
例3:如图,一张矩形纸片,,.点在这张矩形纸片的边上,将纸片折叠,使落在射线上,折痕为,点,分别落在点,处,
(1)若,则的度数为 ;
(2)若,求的长.
知识点3:矩形的判定
矩形的判定有三种方法:
1.定义:有一个角是直角的平行四边形叫做矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
注意:在平行四边形的前提下,加上“一个角是直角”或“对角线相等”都能判定平行四边形是矩形.
例1:在平行四边形中添加下列条件,不能判定四边形是矩形的是
A. B. C. D.
例2 :已知:如图,在中,,是的中线,为的外角的平分线,,交于点.求证:四边形是矩形.
矩形、菱形、正方形(完整)—2、菱形
知识点1:菱形的性质及应用
1、定义:有一组邻边相等的平行四边形是菱形.
2、性质:菱形具有平行四边形的性质,另外,
图示 菱形性质 几何语言
菱形的四条边都相等 四边形为菱形
对角线互相垂直 四边形为菱形
对角线平分一对对角 四边形为菱形
3、菱形的面积
(1)底高
(2)菱形面积为对角线乘积一半,即
对角线之积
例1:下列性质中,菱形对角线不具有的是
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
例2:如图,菱形的对角线,的长分别是6和8,则这个菱形的面积是
A.20 B.24 C.40 D.48
例3:如图,四边形是菱形,对角线,相交于点,且.
(1)菱形的周长为 ;
(2)若,求的长.
知识点2:菱形的判定
图示 判定定理 几何语言
有一组邻边相等的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
对角线互相垂直的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
四边相等的四边形是菱形 平行四边形为菱形
注意:运用前两种方法时,必须先识别四边形是平行四边形,然后再从有一组邻边相等或对角线互相垂直这两个方面来探讨;最后一种判定方法时任意四边形,只要满足了四条边都相等就能证明时菱形.
例1:如图,在中,对角线、相交于点,下列条件中,不能判断这个平行四边形是菱形的是
A. B. C. D.
例2 :在中,点、分别在、上,且.
(1)求证:;
(2)若,求证:四边形为菱形.
矩形、菱形、正方形(完整)——3、正方形
知识点1:正方形的性质及应用
1、定义
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2、性质
图示 性质 几何语言
边 对边平行, 四条边都相等 ∵四边形是正方形 ∴
角 四个角都是直角 ∵四边形是正方形 ∴
对角线 对角线相等并且互相垂直平分,每条对角线平分一组对角 ∵四边形是正方形 ∴
注意:
(1)正方形既是轴对称图形,又是中心对称图形;
(2)正方形既是一组邻边相等的矩形,又是有一个角是直角的菱形,既是矩形又是菱形的四边形是正方形;
(3)正方形的每一条对角线把正方形分成两个全等的等腰三角形,两条对角线把正方形分成四个全等的等腰直角三角形,正方形的对角线与边的夹角是45°.
例1:如图,四边形是正方形,延长到,使,则的度数是 .
例2:如图,在平面直角坐标系中,点、、在坐标轴上,是的中点,四边形是矩形,四边形是正方形,若点的坐标为,则点的坐标为
A. B. C. D.,
知识点2:正方形的判定
正方形的判定
图示 判定定理 几何语言
有一组邻边相等的矩形是正方形 ∵四边形是矩形, ∴四边形是正方形
有一个角是直角的菱形是正方形 ∵四边形是菱形, ∴四边形是正方形
补充:判定四边形是正方形
①对角线互相垂直平分且相等的四边形是正方形;
②对角线互相垂直且相等的平行四边形是正方形;
③对角线相等的菱形是正方形;
④对角线互相垂直的矩形是正方形;
⑤既是菱形又是矩形的四边形是正方形.
例1:小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①,②,③,④中任选两个作为补充条件,使为正方形.现有下列四种选法,你认为其中错误的是
A.②③ B.①③ C.①② D.③④
例2 :如图,在中,对角线、交于点,是延长线上的点,且是等边三角形.
(1)求证:四边形是菱形.
(2)若,求证:四边形是正方形.
矩形练习:
1、检查一个门框是否为矩形,下列方法中正确的是
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量两条对角线,是否互相垂直
D.测量门框的三个角,是否都是直角
2、如图,在中,点在上,,,下列四个判断中不正确的是
A.四边形是平行四边形
B.若,则四边形是矩形
C.若且,则四边形是菱形
D.若平分,则四边形是矩形
3、如图,在中,再添加一个条件 (写出一个即可),是矩形(图形中不再添加辅助线)
4、如图,矩形中,对角线的垂直平分线分别交,于点,,若,,则的长为
A. B. C. D.
5、如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是
A.1 B. C.2 D.
6、如图,在矩形中对角线与相交于点,,垂足为点,,,则的长为
A. B.4 C.6 D.8
7、若矩形两条对角线的夹角是,且较短的边长为3,则这个矩形的面积为 .
8.如图,在矩形中,的平分线交与点,,,则 .
9.如图,矩形的对角线与交于点,过点作的垂线分别交、于、两点,若,,则的长度为 .
10.如图,矩形中,点、分别在、上,,交于点.若,,则图中两块阴影部分的面积之和为 .
11、如图,在矩形中,点在上,平分.
(1)是否为等腰三角形?为什么?
(2)已知,,求的长.
12、如图,在四边形中,,,,,,点从点出发沿边以每秒的速度向点运动, 秒后四边形是矩形.
13、如图,在ABCD中,对角线AC,BD交于点O,且.
求证:ABCD是矩形;
点E在BA延长线上,且,连接DE,求证:.
14、如图,在平行四边形ABCD中,于点E,延长BC至F点使,连接AF,DE,DF.
求证:四边形AEFD是矩形;
若,,,求AE的长。
15、如图,四边形ABCD中,对角线AC、BD相交于点O,,,且.
求证:四边形ABCD是矩形;
,若::2,则的度数是多少?
16、已知:如图,在四边形中,点在边的延长线上,平分,平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
17、如图所示,在中,是上一点,是的中点,过点作交的延长线于点,且,连接.
(1)猜想与有什么数量关系,并说明理由;
(2)当满足什么条件时,四边形是矩形?并说明理由.
菱形练习:
1、下列性质中,菱形具有而矩形不一定具有的是
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边互相垂直
2、如图,四边形是菱形,,,于,则等于
A. B.4 C. D.5
3、如图,平面直角坐标系中,菱形的顶点,,顶点在轴正半轴上,则点的坐标为
A. B. C. D.
4、如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为( )
A . 仅甲正确 B . 仅乙正确
C . 甲、 乙均正确 D . 甲、 乙均错误
5、如图将菱形竖直位置的对角线向右平移,水平位置的对角线向上平移,平移后菱形被分成四块,最大一块与最小一块的面积和记为,其余两块的面积和记为,则与的差是
A. B. C. D.
6、如图,、、、分别是、、、的中点,且,下列结论:①;②四边形是矩形;③平分;④;⑤四边形周长等于.其中正确的个数是
A.1 B.2 C.3 D.4
7、如图,菱形的对角线、相交于点,、分别为边、的中点,连接.若,,则菱形的周长为 .
8、如图,四边形是菱形,对角线,,于点,则的长为 .
9、已知三角形的三条中位线的长分别为、、,则这个三角形的周长是 .
10、矩形的对角线与相交于点,,,分别是,的中点,则的长度为 .
11、已知:如图,在正方形中,点、在对角线上,且,
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
12、如图,矩形的对角线、相交于点,,.
(1)求证:四边形为菱形;
(2)垂直平分线线段于点,,求的长.
13、如图,在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
求证:≌;
求证:四边形ADCF是菱形;
若,,求菱形ADCF的面积.
正方形练习:
1、如图,正方形中,在延长线上取一点,使,连接,则的度数为
A. B. C. D.
2、如图,已知正方形的边长为3,、分别是、边上的点,且,若,则的长为 .
3、如图,在边长为的正方形中,以为边在正方形内作等边,连接并延长交于点,连接.请从,两题中任选一题作答:
.的度数等于 .
.线段的长是 .
4、下列说法正确的是
A.正方形的每一条对角线平分一组对角
B.矩形的对角线互相垂直
C.菱形的四个内角都是直角
D.平行四边形是轴对称图形
5、如图,正方形中,点是对角线上一点,连接,边作交边于于点,且点不与点,重合,作,,垂足分别为点和.
(1)求证:;
(2)求证:.
6、如图,正方形中,是边上一点,是延长线上一点,且,若四边形的面积是,则长是 .
7、下列命题,不正确的是
A.对角线相等且垂直的四边形是正方形
B.有一个角是直角的菱形是正方形
C.顺次连接菱形各边中点所得的四边形是矩形
D.有一个角是的等腰三角形是等边三角形
8、如图,四边形是平行四边形,与相交于点,,添加一个条件: ,可使它成为正方形.
9、已知矩形,给出三个关系式:①;②;③,如果选择关系式 作为条件(写出一个即可),那么可以判定矩形为正方形,理由是 .
10、如图,在矩形中,点在边上,连结,将矩形沿折叠,点的对称点落在边上,连结.求证:四边形是正方形.
11、下列说法不能判断是正方形的是
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
12、已知平行四边形,对角线、相交于点,且,延长至点,使,连接.
(1)当时,求证:;
(2)当时,求证:四边形是正方形.
13、如图,在中,,的垂直平分线交于点,交于点,且,添加一个条件,仍不能证明四边形为正方形的是
A. B. C. D.
14、如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作,求证:四边形OCED是正方形.
矩形、菱形、正方形(完整)——1、矩形
知识点1:矩形的定义
有一个角是直角的平行四边形叫做矩形.
注意:矩形定义的两个要素:①是平行四边形;
②有一个角是直角.即矩形首先是一个平行四边形,然后增加一个角是直角这个特殊条件.
例1:矩形的对角线、相交于点,,,则的周长为
A.12 B.14 C.16 D.18
【解答】解:四边形是矩形,
,,,
,
,
,
是等边三角形,
,
的周长;
故选:.
知识点2:矩形的性质
矩形的性质包括四个方面:1.矩形具有平行四边形的所有性质;
2.矩形的对角线相等;
3.矩形的四个角都是直角;
4.矩形是轴对称图形,它有两条对称轴.
注意:(1)矩形是特殊的平行四边形,因而也是中心对称图形.过中心的任意直线可将矩形分成完全全等的两部分.
(2)矩形也是轴对称图形,有两条对称轴(分别通过对边中点的直线).对称轴的交点就是对角线的交点(即对称中心).
(3)矩形是特殊的平行四边形,矩形具有平行四边形的所有性质,从而矩形的性质可以归结为从三个方面看:从边看,矩形对边平行且相等;从角看,矩形四个角都是直角;从对角线看,矩形的对角线互相平分且相等.
例2:如图,在矩形中,,,点为边上任意一点,过点作,,垂足分别为、,则 .
【解答】解:连接,如图:
四边形是矩形,
,,,,
,,
,,,
,
;
故答案为:.
例3:如图,一张矩形纸片,,.点在这张矩形纸片的边上,将纸片折叠,使落在射线上,折痕为,点,分别落在点,处,
(1)若,则的度数为 ;
(2)若,求的长.
【解答】解:(1)四边形是矩形,
,
,,
由折叠的性质得:,
;
故答案为:70;
(2),,
,
四边形是矩形,
,,
,
由翻折不变性可知,,
,
,
,,
在中,由勾股定理得:,
,
由翻折不变性可知,,
.
知识点3:矩形的判定
矩形的判定有三种方法:
1.定义:有一个角是直角的平行四边形叫做矩形.
2.对角线相等的平行四边形是矩形.
3.有三个角是直角的四边形是矩形.
注意:在平行四边形的前提下,加上“一个角是直角”或“对角线相等”都能判定平行四边形是矩形.
例1:在平行四边形中添加下列条件,不能判定四边形是矩形的是
A. B. C. D.
【解答】解:
、四边形是平行四边形,,
四边形是矩形,故本选项不符合题意;
、根据四边形是平行四边形和不能推出四边形是矩形,故本选项符合题意;
、四边形是平行四边形,,
四边形是矩形,故本选项不符合题意;
、,
,
四边形是平行四边形,
,,
,
四边形是矩形,故本选项不符合题意;
故选:.
例2 :已知:如图,在中,,是的中线,为的外角的平分线,,交于点.求证:四边形是矩形.
【解答】证明:在中,,是边的中线,
,,
,
为的外角的平分线,
,
,
,
,
四边形为矩形.
矩形、菱形、正方形(完整)——2菱形
知识点1:菱形的性质及应用
1、定义:有一组邻边相等的平行四边形是菱形.
2、性质:菱形具有平行四边形的性质,另外,
图示 菱形性质 几何语言
菱形的四条边都相等 四边形为菱形
对角线互相垂直 四边形为菱形
对角线平分一对对角 四边形为菱形
3、菱形的面积
(1)底高
(2)菱形面积为对角线乘积一半,即
对角线之积
例1:下列性质中,菱形对角线不具有的是
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
【解答】解:菱形对角线具有的性质有:对角线互相垂直,对角线互相平分,
对角线所在直线是对称轴.
故,,正确,错误.
故选:.
例2:如图,菱形的对角线,的长分别是6和8,则这个菱形的面积是
A.20 B.24 C.40 D.48
【解答】解:菱形的对角线,的长分别是6和8,
菱形的面积.
故选:.
例3:如图,四边形是菱形,对角线,相交于点,且.
(1)菱形的周长为 ;
(2)若,求的长.
【解答】解:(1)四边形是菱形,,
菱形的周长为:8;
故答案为8.
(2)四边形是菱形,,,
,,
,
.
知识点2:菱形的判定
图示 判定定理 几何语言
有一组邻边相等的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
对角线互相垂直的平行四边形是菱形 四边形为平行四边形 平行四边形为菱形
四边相等的四边形是菱形 平行四边形为菱形
注意:运用前两种方法时,必须先识别四边形是平行四边形,然后再从有一组邻边相等或对角线互相垂直这两个方面来探讨;最后一种判定方法时任意四边形,只要满足了四条边都相等就能证明时菱形.
例1:如图,在中,对角线、相交于点,下列条件中,不能判断这个平行四边形是菱形的是
A. B. C. D.
【解答】解:、邻边相等的平行四边形是菱形,故选项不符合题意;
、对角线平分对角的平行四边形是菱形,故选项不符合题意;
、由不一定能够判断这个平行四边形是菱形,故选项符合题意;
、对角线互相垂直平分的平行四边形是菱形,故选项不符合题意.
故选:.
例2 :在中,点、分别在、上,且.
(1)求证:;
(2)若,求证:四边形为菱形.
【解答】证明:(1)四边形是平行四边形,
,,
在和中,
,
;
(2)四边形是平行四边形,
,,
,
,
四边形是平行四边形,
又,
四边形为菱形.
矩形、菱形、正方形(完整)——3、正方形
知识点1:正方形的性质及应用
1、定义
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2、性质
图示 性质 几何语言
边 对边平行, 四条边都相等 ∵四边形是正方形 ∴
角 四个角都是直角 ∵四边形是正方形 ∴
对角线 对角线相等并且互相垂直平分,每条对角线平分一组对角 ∵四边形是正方形 ∴
注意:
(1)正方形既是轴对称图形,又是中心对称图形;
(2)正方形既是一组邻边相等的矩形,又是有一个角是直角的菱形,既是矩形又是菱形的四边形是正方形;
(3)正方形的每一条对角线把正方形分成两个全等的等腰三角形,两条对角线把正方形分成四个全等的等腰直角三角形,正方形的对角线与边的夹角是45°.
例1:如图,四边形是正方形,延长到,使,则的度数是 .
【解答】解:四边形是正方形,
,
,
,
.
故答案为:.
例2:如图,在平面直角坐标系中,点、、在坐标轴上,是的中点,四边形是矩形,四边形是正方形,若点的坐标为,则点的坐标为
A. B. C. D.,
【解答】解:过作轴于,
四边形是矩形,四边形是正方形,
,,
,
,
,
,
,,
,
是的中点,
,
点的坐标为,
,
,,
同理,
,,
,
点的坐标为,
故选:.
知识点2:正方形的判定
正方形的判定
图示 判定定理 几何语言
有一组邻边相等的矩形是正方形 ∵四边形是矩形, ∴四边形是正方形
有一个角是直角的菱形是正方形 ∵四边形是菱形, ∴四边形是正方形
补充:判定四边形是正方形
①对角线互相垂直平分且相等的四边形是正方形;
②对角线互相垂直且相等的平行四边形是正方形;
③对角线相等的菱形是正方形;
④对角线互相垂直的矩形是正方形;
⑤既是菱形又是矩形的四边形是正方形.
例1:小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①,②,③,④中任选两个作为补充条件,使为正方形.现有下列四种选法,你认为其中错误的是
A.②③ B.①③ C.①② D.③④
【解答】解:、四边形是平行四边形,
当②时,平行四边形是矩形,
当时,这是矩形的性质,无法得出四边形是正方形,故此选项错误,符合题意;
、四边形是平行四边形,
当①时,平行四边形是菱形,
当③时,菱形是正方形,故此选项正确,不合题意;
、四边形是平行四边形,
当①时,平行四边形是菱形,
当②时,菱形是正方形,故此选项正确,不合题意;
、四边形是平行四边形,
当③时,平行四边形是矩形,
当④时,矩形是正方形,故此选项正确,不合题意.
故选:.
例2 :如图,在中,对角线、交于点,是延长线上的点,且是等边三角形.
(1)求证:四边形是菱形.
(2)若,求证:四边形是正方形.
【解答】证明:(1),
,
是等边三角形,
(三线合一)
即,
是菱形;
(2)是等边三角形,
由(1)知,,
,是直角三角形
,
,
,
,
是菱形,
,
菱形是正方形.
矩形练习:
1、检查一个门框是否为矩形,下列方法中正确的是
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.测量两条对角线,是否互相垂直
D.测量门框的三个角,是否都是直角
【解析】对角线相等的平行四边形是矩形,
故不符合题意;
对角线互相平分的四边形是平行四边形,
故不符合题意,
两条对角线互相垂直的四边形不一定是矩形,
故不符合题意;
三个角都是直角的四边形是矩形,
故符合题意;
故选:.
2、如图,在中,点在上,,,下列四个判断中不正确的是
A.四边形是平行四边形
B.若,则四边形是矩形
C.若且,则四边形是菱形
D.若平分,则四边形是矩形
【解析】因为,,所以四边形是平行四边形.故正确.
,四边形是平行四边形,所以四边形是矩形.故正确.
若且,则四边形是菱形,故正确;
因为平分,所以,又因为四边形是平行四边形,所以是菱形.故错误.
故选:.
3、如图,在中,再添加一个条件 (写出一个即可),是矩形(图形中不再添加辅助线)
【解析】添加的条件是,
理由是:,四边形是平行四边形,
平行四边形是矩形,
故答案为:
4、如图,矩形中,对角线的垂直平分线分别交,于点,,若,,则的长为
A. B. C. D.
【解析】如图,连接,设与交点为,
是的垂直平分线,
,,
四边形是矩形,
,,
,
在和中,
,
,
,
,,
,
,
故选:.
5、如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是
A.1 B. C.2 D.
【解析】连接,如图所示:
四边形是矩形,
,,,,
,
,
设,则,
在中,由勾股定理得:,
解得:,
即;
故选:.
6、如图,在矩形中对角线与相交于点,,垂足为点,,,则的长为
A. B.4 C.6 D.8
【解析】四边形是矩形,
,
, 故选:.
7、若矩形两条对角线的夹角是,且较短的边长为3,则这个矩形的面积为 .
【解答】解:如图所示:
四边形是矩形,
,,,,
,
又,
是等边三角形,
,
,
矩形的面积
故答案为:
8.如图,在矩形中,的平分线交与点,,,则 .
【解答】解:四边形是矩形,
,,,,
,
,
,
在中,.
故答案为.
9.如图,矩形的对角线与交于点,过点作的垂线分别交、于、两点,若,,则的长度为 .
【解答】解:四边形是矩形,
,
,
,
,,
,,
四边形是矩形,
,,
,
,
又中,,
,
,
故答案为:2.
10.如图,矩形中,点、分别在、上,,交于点.若,,则图中两块阴影部分的面积之和为 .
【解答】解:如图,过点作于,交于,
,,
,
,且,,
易证:四边形是矩形,四边形是矩形,四边形是矩形,四边形是矩形
,,,,,
,
两块阴影部分的面积之和为10 故答案为10
11、如图,在矩形中,点在上,平分.
(1)是否为等腰三角形?为什么?
(2)已知,,求的长.
【解答】解:(1)是等腰三角形,
理由是:四边形是矩形,
,
,
平分,
,
,
,
即是等腰三角形.
(2)四边形是矩形,
,
,
,
,
由勾股定理得:,
即.
12、、如图,在四边形中,,,,,,点从点出发沿边以每秒的速度向点运动, 秒后四边形是矩形.
【解析】当时,四边形是矩形,
此时:,,
在中,,
所以3秒后四边形是矩形,
故答案为:3
13、如图,在ABCD中,对角线AC,BD交于点O,且.
【解析】求证:ABCD是矩形;
点E在BA延长线上,且,连接DE,求证:.
证明:四边形ABCD是平行四边形,
,,
,
,
平行四边形ABCD是矩形;
四边形ABCD是平行四边形,
,,
又,
,
四边形DEAC是平行四边形,
.
14、如图,在平行四边形ABCD中,于点E,延长BC至F点使,连接AF,DE,DF.
求证:四边形AEFD是矩形;
若,,,求AE的长。
【解析】.证明:,
.
即 .
在 ABCD中,且,
且.
四边形AEFD是平行四边形.
,
.
四边形AEFD是矩形;
解:四边形AEFD是矩形,,
.
,,
.
.
,
的面积.
.
15、如图,四边形ABCD中,对角线AC、BD相交于点O,,,且.
求证:四边形ABCD是矩形;
,若::2,则的度数是多少?
【解析】证明:,
四边形ABCD是平行四边形,
,
,
,
四边形ABCD是矩形;
解:,::2,
,
,
,
四边形ABCD是矩形,
,
.
16、已知:如图,在四边形中,点在边的延长线上,平分,平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
【解析】证明:
(1)平分、平分,
,,
,
,,
,,
,,
;
(2)点为的中点,
,
又,
四边形是平行四边形,
平分、平分,
,
,
即,
四边形是矩形.
17、如图所示,在中,是上一点,是的中点,过点作交的延长线于点,且,连接.
(1)猜想与有什么数量关系,并说明理由;
(2)当满足什么条件时,四边形是矩形?并说明理由.
【解析】(1)猜想:,
证明:,
,
是的中点,
,
在和中,
,
,
,
,
;
(2)猜想:当是以为顶点的等腰三角形时,四边形是矩形;
证明:连接,
,,
四边形是平行四边形,
同理可得四边形是平行四边形,
,
是等腰三角形,即,
,
是矩形.
菱形练习:
1、下列性质中,菱形具有而矩形不一定具有的是
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边互相垂直
【解答】解:(A)对角线相等是矩形具有的性质,菱形不一定具有;
(B)对角线互相平分是菱形和矩形共有的性质;
(C)对角线互相垂直是菱形具有的性质,矩形不一定具有;
(D)邻边互相垂直是矩形具有的性质,菱形不一定具有.
故选:.
2、如图,四边形是菱形,,,于,则等于
A. B.4 C. D.5
【解答】解:四边形是菱形,
,,,
,
,
,
,
故选:.
3、如图,平面直角坐标系中,菱形的顶点,,顶点在轴正半轴上,则点的坐标为
A. B. C. D.
【解答】解:菱形的顶点,,
,,
,
点的坐标为
故选:.
4、如图,是一张平行四边形纸片, 要求利用所学知识作出一个菱形, 甲、 乙两位同学的作法如下: 则关于甲、 乙两人的作法, 下列判断正确的为( )
A . 仅甲正确 B . 仅乙正确
C . 甲、 乙均正确 D . 甲、 乙均错误
【解答】解: 甲的作法正确;
四边形是平行四边形,
,
,
是的垂直平分线,
,
在和中,
,
,
,
又,
四边形是平行四边形,
,
四边形是菱形;
乙的作法正确;
,
,,
平分,平分,
,,
,,
,,
,且,
四边形是平行四边形,
,
平行四边形是菱形;
故选:C.
5、如图将菱形竖直位置的对角线向右平移,水平位置的对角线向上平移,平移后菱形被分成四块,最大一块与最小一块的面积和记为,其余两块的面积和记为,则与的差是
A. B. C. D.
【解答】解:如图,作关于的对称线段,作关于的对称线段,
由对称性可知,图中对应颜色的部分面积相等,
与的差,
,,
,
故选:.
6、如图,、、、分别是、、、的中点,且,下列结论:①;②四边形是矩形;③平分;④;⑤四边形周长等于.其中正确的个数是
A.1 B.2 C.3 D.4
【解答】解:、、、分别是、、、的中点,
,,,,
,
,,
四边形是菱形,
①,正确;
②四边形是矩形,错误;
③平分,正确;
④当,如图所示:,分别为,中点,
连接,延长交上一点,
,,
,故本小题错误;
⑤四边形周长等于,正确;
综上所述,①③⑤共3个正确;
故选:.
7、如图,菱形的对角线、相交于点,、分别为边、的中点,连接.若,,则菱形的周长为 .
【解答】解:、是和的中点,即是的中位线,
,
,,
在中,,
所以菱形的周长为8,
故答案为:8
8、如图,四边形是菱形,对角线,,于点,则的长为 .
【解答】解:四边形是菱形,
,,,
,
,
.
9、已知三角形的三条中位线的长分别为、、,则这个三角形的周长是 .
【解答】解:三角形的三条中位线的长分别是、、,
三角形的三条边分别是、、.
这个三角形的周长.
故答案是:42.
10、矩形的对角线与相交于点,,,分别是,的中点,则的长度为 .
【解答】解:四边形为矩形,
,
又因为矩形对角线的交点等分对角线,
,
又在中,,分别是,的中点,
为的中位线,
,
故答案为:1.
11、已知:如图,在正方形中,点、在对角线上,且,
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
【解答】(1)证明:正方形中,对角线,
,
.
,
.
四边形是菱形;
(2)解:在中,由勾股定理,得
,
,
,
四边形的面积
.
12、如图,矩形的对角线、相交于点,,.
(1)求证:四边形为菱形;
(2)垂直平分线线段于点,,求的长.
【解析】证明:(1),,
四边形是平行四边形,
矩形的对角线,相交于点,
,
四边形为菱形.
(2)过作,
矩形的对角线、相交于点,
,
垂直平分线线段于点,
,
是等边三角形,
,
,
,
,,
,
.
13、如图,在中,,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
求证:≌;
求证:四边形ADCF是菱形;
若,,求菱形ADCF的面积.
解:证明:,
,
是AD的中点,AD是BC边上的中线,
,,
在和中,
,
≌;
证明:由知,≌,
则
,
.
,
四边形ADCF是平行四边形,
,D是BC的中点,E是AD的中点,
,
四边形ADCF是菱形;
正方形练习:
1、如图,正方形中,在延长线上取一点,使,连接,则的度数为
A. B. C. D.
【解答】解:四边形是正方形,
,
,
,
,
故选:.
2、如图,已知正方形的边长为3,、分别是、边上的点,且,若,则的长为 .
【解答】解:如图,将绕点按逆时针方向旋转得到.
绕点逆时针旋转得到,
,,,
,
点,点,点三点共线,
,
,
,
在和中,
,
;
设,
,,
,,
.
在中,由勾股定理得,
即,
解得:,
则的长为,
故答案为:.
3、如图,在边长为的正方形中,以为边在正方形内作等边,连接并延长交于点,连接.请从,两题中任选一题作答:
.的度数等于 .
.线段的长是 .
【解答】解:.△为等边三角形,
,,
四边形是正方形,
,,
,,
,
,
,
故答案为:;
.作,与交于点,如下图,则,
设,
,
,
,
,
,
,
,
,
解得,,
即,
故答案为:.
4、下列说法正确的是
A.正方形的每一条对角线平分一组对角
B.矩形的对角线互相垂直
C.菱形的四个内角都是直角
D.平行四边形是轴对称图形
【解答】解:.正方形的每一条对角线平分一组对角,故选项符合题意;
.矩形的对角线不一定互相垂直,故选项不符合题意;
.菱形的四个内角不一定都是直角,故选项不符合题意;
.平行四边形不一定是轴对称图形,故选项不符合题意;
故选:.
5、如图,正方形中,点是对角线上一点,连接,边作交边于于点,且点不与点,重合,作,,垂足分别为点和.
(1)求证:;
(2)求证:.
【解答】证明:(1)四边形为正方形,
平分,
又,,
.
(2),,,,
四边形为正方形,
,即.
,
,
.
,,
.
在和中,,
,
.
6、如图,正方形中,是边上一点,是延长线上一点,且,若四边形的面积是,则长是 .
【解答】解:四边形是正方形,
,,
在和中,
,
,
,
四边形的面积是,
正方形的面积是,
,
7、下列命题中,不正确的是
A.对角线相等且垂直的四边形是正方形
B.有一个角是直角的菱形是正方形
C.顺次连接菱形各边中点所得的四边形是矩形
D.有一个角是的等腰三角形是等边三角形
【解答】解:、对角线互相平分、相等且垂直的四边形是正方形,本选项说法不正确,符合题意;
、有一个角是直角的菱形是正方形,本选项说法正确,不符合题意;
、顺次连接菱形各边中点所得的四边形是矩形,本选项说法正确,不符合题意;
、有一个角是的等腰三角形是等边三角形,选项说法不正确,不符合题意;
故选:.
8、如图,四边形是平行四边形,与相交于点,,添加一个条件: ,可使它成为正方形.
【解答】解:因为四边形是平行四边形,,
所以是菱形,
如果,
那么四边形是正方形.
故答案为:.
9、已知矩形,给出三个关系式:①;②;③,如果选择关系式 作为条件(写出一个即可),那么可以判定矩形为正方形,理由是 .
【解答】解:四边形是矩形,,
矩形为正方形(对角线互相垂直的矩形是正方形),
故答案为:③,对角线互相垂直的矩形是正方形.
10、如图,在矩形中,点在边上,连结,将矩形沿折叠,点的对称点落在边上,连结.求证:四边形是正方形.
【解答】证明:四边形是矩形,
.
由折叠,得
.
四边形是矩形.
,
四边形是正方形.
11、下列说法不能判断是正方形的是
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
【解答】解:.对角线互相垂直且相等的平行四边形是正方形,故选项不符合题意;
.对角线互相垂直的矩形是正方形,故选项不符合题意;
.对角线相等的菱形是正方形,故选项不符合题意;
.对角线互相垂直平分的四边形是菱形,菱形不一定是正方形,故选项符合题意;
故选:.
12、已知平行四边形,对角线、相交于点,且,延长至点,使,连接.
(1)当时,求证:;
(2)当时,求证:四边形是正方形.
【解答】(1)证明:四边形是平行四边形,
又,
四边形是菱形.
.
又,
,
;
(2)证明:四边形是平行四边形,
,,
又,
,,
四边形是平行四边形.
,
平行四边形是矩形,
又,
,
矩形是正方形.
13、如图,在中,,的垂直平分线交于点,交于点,且,添加一个条件,仍不能证明四边形为正方形的是
A. B. C. D.
【解答】解:垂直平分,
,,
,
,
四边形是菱形;
当时,
,
则时,菱形是正方形.
,,
菱形是正方形.
故选项正确,但不符合题意;
当时,利用正方形的判定得出,菱形是正方形,故选项正确,但不符合题意;
当时,利用正方形的判定得出,菱形是正方形,故选项正确,但不符合题意;
当时,无法得出菱形是正方形,故选项错误,符合题意.
故选:.
14、如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作,求证:四边形OCED是正方形.
【解析】证明:,,
四边形OCED是平行四边形,
四边形ABCD是正方形,
,,
,
四边形OCED是正方形.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
