人教版五年级下册数学最大公因数和最小公倍数课件(共36张PPT)
文档属性
| 名称 | 人教版五年级下册数学最大公因数和最小公倍数课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 479.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 11:37:28 | ||
图片预览









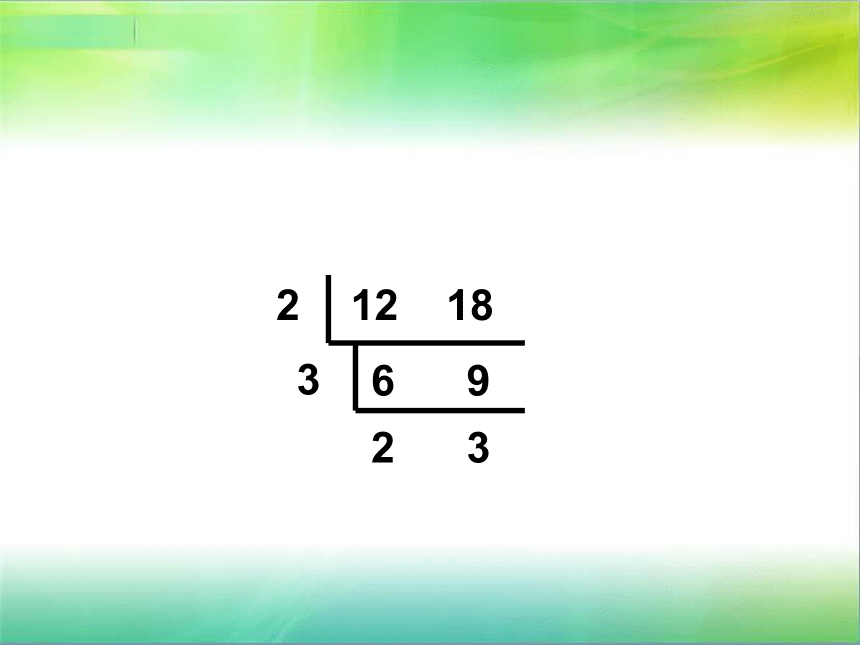


文档简介
(共36张PPT)
找最大公因数
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝长多少厘米?
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
1厘米
每段铁丝长多少厘米?
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝长多少厘米?
2厘米
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝长多少厘米?
4厘米
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝最长多少厘米?
每段铁丝长多少厘米?
4厘米
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝最长多少厘米?
每段铁丝长多少厘米?
8的因数: 1,2,4,8。
12的因数:1,2,3,4,6,12。
1 2 4
1 2 4
8和12的公因数: 1,2,4。
最大公因数
有三根铁丝,分别长8厘米、12厘米、6厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余,每段铁丝最长多少厘米?
8的因数: 1,2,4,8。
12的因数:1,2,3,4,6,12。
6的因数: 1,2,3,6。
6,8和12的最大公因数:2
个数相同的因数叫做这 个数的公因数。其中最大的公因数叫做这 个数的最大公因数。
几
几
几
两
两
两
短除法求最大公因数
12 18
6 9
2 3
2
3
两根电线分别长24米和16米,现在将这两根电线剪成相等的小段,并且没有剩余,剪成的小段最长可以是多少米?
16和24的最大公因数是:8,即每小段最长为8米;
一个长方体木块,长30cm,宽21cm,高18cm。把它切成大小相等的小正方体,不准有剩余,那么正方体小木块棱长最大是多少 能切成多少块
小正方体棱长最大是30、21、18的最大公因数,即:
(30,21,18)=3(厘米)
能切:
(30÷3)×(21÷3)×(18÷3)=420(块)
提示:
如果是求几个数的公因数,且要求是“最大“最多”的人数、份数、每份数等问题,就是求这几个数的最大公因数。
求几个数的最大公因数和求两个数的最大公因数方法相同。
一个长方体木块,长45cm,宽30cm,高24cm。把它切成大小相等的小正方体,不准有剩余,那么正方体小木块棱长最大是多少 能切成多少块
解答:
45的因数:1,3,5,9,15,45
30的因数:1,2,3,5,6,10,15,30
24的因数:1,2,3,4,6,8,12,24
45、30和24的最大公因数是3,所以小正方体的最大棱长是3cm。
45×30×24÷(3×3×3)
=32400÷27
=1200(块)
答:正方体小木块棱长最大是3cm,能切成1200块。
(45÷3)×(30÷3)×(24÷3)
=15×10×8
=1200 (块)
通过求最大公因数解题 的应用题:
分组问题、分东西,裁最大的正方形,铁丝分段
一般题目中会出现:
最大、最多、最长等字眼
题目常常给几个较大的数,求较小的数,就是要你求最大公因数
找最小公倍数
洋洋就要放假了,很想让爸爸和妈妈带他出去玩。可洋洋的妈妈从七月一日起每工作3天休息一天,爸爸从七月一日起每工作5天休息一天,他打算等爸爸和妈妈同时休息时,全家一块儿去南湖公园玩。
在这一个月里,他们可以选哪些日子去呢?
共同的休息日:12,24
其中最早的一天:12
“妈妈的休息日”有什么特点?
4的倍数:
妈妈的休息日:
4,8,12,16,20,24,28
4的倍数还有吗?有多少个?
……
“爸爸的休息日”有什么特点?
6的倍数:
爸爸的休息日:
6,12,18,24,30
6的倍数有多少个?
……
这些数和4,6有什么关系?
4和6的公倍数:
他们共同的休息日:
12,24
4和6的公倍数还能找出一些来吗?可以找多少?
……
最小公倍数:
其中最早的一天:
12
4的倍数:4,8,12,16,20,24,28,…
6的倍数:6,12,18,24,30,…
4和6的公倍数:12, 24,…
4和6的最小公倍数:12
利用最小公倍数解决生活问题
五⑴班同学参加植树劳动,按6人一组或8人一组都正好分完。五⑴班参加植树的至少有多少人?
至少
最小
6的倍数有 。
8的倍数有 。
6和8的公倍数有 。
6和8的最小公倍数是 。
6,12,18,24,30,36,42,48,......
8,16,24,32,40,48,......
24,48
24
答:五⑴班参加植树的至少有24人。
南湖公园是1路和6路汽车的起点站。1路汽车每3分钟发车一次,6路汽车每5分钟发车一次。这两路汽车同时发车以后,至少再过多久又同时发车?
3的倍数有 。
5的倍数有 。
3和5的公倍数有 。
3和5的最小公倍数是 。
3,6,9,12,15,18,21,24,27,30,......
5,10,15,20,25,30,......
15,30,……
15
答:至少再过15分钟又同时发车。
通过求最大公因数解题 的应用题:
分组问题、分东西,裁最大的正方形,铁丝分段
一般题目中会出现:
最大、最多、最长等字眼
题目常常给几个较大的数,求较小的数,就是要你求最大公因数
例1:一张硬纸板长60厘米,宽56厘米。现在需要把它剪成若干个大小相同的最大的正方形,不许有剩余。问:最大正方形的边长是多少?
要求把它剪成若干个大小相同的最大正方形,实际上就是求硬纸板的长和宽的最大公因数。(60, 56)=4,所以最大正方形的边长是 4 厘米。
答:最大正方形的边长是 4 厘米。
例2:甲、乙、丙三辆汽车在环形马路上同向行驶,甲车行一周要36分钟,乙车行一周要30分钟,丙车行一周要48分钟。三辆汽车同时从同一个起点出发,问:这三辆汽车至少要多长时间才能同时回到出发地?
要求这三辆汽车多长时间才能同时回到出发地,这个时间必定同时是 36,30,48 的倍数。因为问至少要多长时间,所以应是 36,30, 48 的最小公倍数。[36,30,48]=720,720 分钟也就是 12 小时。
答:这三辆汽车至少要720分钟(12小时)才能同时回到出发地。
例3:—盒围棋子,4个4个地数多1个,5个5个地数多1个,6个6个地数还多1个,又知棋子总数在150到200之间,求这盒棋子的总数。
如果从总数中取出1个,余下的总数便是4,5, 6的公倍数。因为4,5,6的最小公倍数是60,又知棋子总数在150到200之间,符合条件的只有1个,即:60×3+1=181 (个)。
例4:用96朵红玫现花和72朵白玫瑰花做花束,已知每个花束里的红玫瑰花的朵数相同,自玫瑰花的朵数也相同。最多可以做多少个花束?每个花束里至少有多少朵花
要把96朵红玻瑰花和72朵白玫瑰花做成花束,且每束花里的红玻瑰花朵数相同,白玫瑰花朵数也相同,那么做成花束的个数一定是96和72 的公因数,又要求花束的个数最多,所以花束的个数应是96和72的最大公因数。
解:最多可以做多少个花束?(96,72)=24(个)
每个花束里有几朵红玫瑰花? 96÷24=4(朵)
每个花束里有几朵白玫瑰花? 72 ÷ 24=3(朵)
每个花束里至少有几朵花? 4+3=7(朵)
答:最多可以做24个花束,每个花束里至少有7朵花。
例5:为了响应“植树造林,绿化荒山”的号召,六(1)班同学在老师的带领下去山坡上种树,种完树后,老师让同学们数数一共种了多少棵树,结果大家发现: 2棵2棵地数还剩 1棵,3棵3棵地数还剩2棵,4棵4棵地数还剩3棵。5棵5棵地数还剩4棵。 6棵6棵地数还剩5棵, 7棵7棵地数正好数完。那么他们至少种了多少棵树?
由题可知,如果多种1棵,就可以同时被2,3, 4,5, 6 整除,但又必须考虑实际的数能被7整除。[2, 3,4,5,6]=60,60-1=59 不能被7整除,不符合题意;60×2=120, 120-1=119, 119 能被 7 整除,符合题意。所以至少种了 119 棵树。
例6:公路边上有一排电线杆,从头到尾共25根。每相邻两根电线杆间的距离原来都是45米,现在要改为60米,可以有几根电线杆不需要移动?
不需要移动的电线杆距第一根的距离一定既是45的倍数,又是60的倍数。要先求45和60的最小公倍数,以及这条公路的全长,再求可以有几根电线杆不需要移动。
解:从第一根起至少相隔多少米的一根电线杆不需要移动?
[45,60]=180(米)
公路全长多少米?45×(25-1)=1080(米)
可以有几根电线杆不需要移动?1080÷180+1=7(根)
答:可以有7 根电线杆不需要移动。
例7、今有梨320个、糖果240个、饼干200个,将这些东西分成相同的礼品包送给儿童,但包数要最多,则每包有多少个梨?有多少个糖果?有多少个饼干?
320、240和200的最大公因数是:40
梨:320÷40=8(个)
糖果:240÷40=6 (个)
饼干:200÷40=5(个)
答:每包有8个梨。有6个糖果。有5个饼干。
例8、一筐鸡蛋,3个3个数,最后多1个;5个5个数,最后多1个;6个6个数,最后也多1个。这些鸡蛋至少有多少个?
3、5和6的最小公倍数是:30
30+1=31(个)
答:这些鸡蛋至少有31个。
找最大公因数
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝长多少厘米?
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
1厘米
每段铁丝长多少厘米?
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝长多少厘米?
2厘米
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝长多少厘米?
4厘米
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝最长多少厘米?
每段铁丝长多少厘米?
4厘米
有两根铁丝,分别长8厘米、12厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余。
每段铁丝最长多少厘米?
每段铁丝长多少厘米?
8的因数: 1,2,4,8。
12的因数:1,2,3,4,6,12。
1 2 4
1 2 4
8和12的公因数: 1,2,4。
最大公因数
有三根铁丝,分别长8厘米、12厘米、6厘米,要把它们截成同样大小的小段(取整厘米数),不能有剩余,每段铁丝最长多少厘米?
8的因数: 1,2,4,8。
12的因数:1,2,3,4,6,12。
6的因数: 1,2,3,6。
6,8和12的最大公因数:2
个数相同的因数叫做这 个数的公因数。其中最大的公因数叫做这 个数的最大公因数。
几
几
几
两
两
两
短除法求最大公因数
12 18
6 9
2 3
2
3
两根电线分别长24米和16米,现在将这两根电线剪成相等的小段,并且没有剩余,剪成的小段最长可以是多少米?
16和24的最大公因数是:8,即每小段最长为8米;
一个长方体木块,长30cm,宽21cm,高18cm。把它切成大小相等的小正方体,不准有剩余,那么正方体小木块棱长最大是多少 能切成多少块
小正方体棱长最大是30、21、18的最大公因数,即:
(30,21,18)=3(厘米)
能切:
(30÷3)×(21÷3)×(18÷3)=420(块)
提示:
如果是求几个数的公因数,且要求是“最大“最多”的人数、份数、每份数等问题,就是求这几个数的最大公因数。
求几个数的最大公因数和求两个数的最大公因数方法相同。
一个长方体木块,长45cm,宽30cm,高24cm。把它切成大小相等的小正方体,不准有剩余,那么正方体小木块棱长最大是多少 能切成多少块
解答:
45的因数:1,3,5,9,15,45
30的因数:1,2,3,5,6,10,15,30
24的因数:1,2,3,4,6,8,12,24
45、30和24的最大公因数是3,所以小正方体的最大棱长是3cm。
45×30×24÷(3×3×3)
=32400÷27
=1200(块)
答:正方体小木块棱长最大是3cm,能切成1200块。
(45÷3)×(30÷3)×(24÷3)
=15×10×8
=1200 (块)
通过求最大公因数解题 的应用题:
分组问题、分东西,裁最大的正方形,铁丝分段
一般题目中会出现:
最大、最多、最长等字眼
题目常常给几个较大的数,求较小的数,就是要你求最大公因数
找最小公倍数
洋洋就要放假了,很想让爸爸和妈妈带他出去玩。可洋洋的妈妈从七月一日起每工作3天休息一天,爸爸从七月一日起每工作5天休息一天,他打算等爸爸和妈妈同时休息时,全家一块儿去南湖公园玩。
在这一个月里,他们可以选哪些日子去呢?
共同的休息日:12,24
其中最早的一天:12
“妈妈的休息日”有什么特点?
4的倍数:
妈妈的休息日:
4,8,12,16,20,24,28
4的倍数还有吗?有多少个?
……
“爸爸的休息日”有什么特点?
6的倍数:
爸爸的休息日:
6,12,18,24,30
6的倍数有多少个?
……
这些数和4,6有什么关系?
4和6的公倍数:
他们共同的休息日:
12,24
4和6的公倍数还能找出一些来吗?可以找多少?
……
最小公倍数:
其中最早的一天:
12
4的倍数:4,8,12,16,20,24,28,…
6的倍数:6,12,18,24,30,…
4和6的公倍数:12, 24,…
4和6的最小公倍数:12
利用最小公倍数解决生活问题
五⑴班同学参加植树劳动,按6人一组或8人一组都正好分完。五⑴班参加植树的至少有多少人?
至少
最小
6的倍数有 。
8的倍数有 。
6和8的公倍数有 。
6和8的最小公倍数是 。
6,12,18,24,30,36,42,48,......
8,16,24,32,40,48,......
24,48
24
答:五⑴班参加植树的至少有24人。
南湖公园是1路和6路汽车的起点站。1路汽车每3分钟发车一次,6路汽车每5分钟发车一次。这两路汽车同时发车以后,至少再过多久又同时发车?
3的倍数有 。
5的倍数有 。
3和5的公倍数有 。
3和5的最小公倍数是 。
3,6,9,12,15,18,21,24,27,30,......
5,10,15,20,25,30,......
15,30,……
15
答:至少再过15分钟又同时发车。
通过求最大公因数解题 的应用题:
分组问题、分东西,裁最大的正方形,铁丝分段
一般题目中会出现:
最大、最多、最长等字眼
题目常常给几个较大的数,求较小的数,就是要你求最大公因数
例1:一张硬纸板长60厘米,宽56厘米。现在需要把它剪成若干个大小相同的最大的正方形,不许有剩余。问:最大正方形的边长是多少?
要求把它剪成若干个大小相同的最大正方形,实际上就是求硬纸板的长和宽的最大公因数。(60, 56)=4,所以最大正方形的边长是 4 厘米。
答:最大正方形的边长是 4 厘米。
例2:甲、乙、丙三辆汽车在环形马路上同向行驶,甲车行一周要36分钟,乙车行一周要30分钟,丙车行一周要48分钟。三辆汽车同时从同一个起点出发,问:这三辆汽车至少要多长时间才能同时回到出发地?
要求这三辆汽车多长时间才能同时回到出发地,这个时间必定同时是 36,30,48 的倍数。因为问至少要多长时间,所以应是 36,30, 48 的最小公倍数。[36,30,48]=720,720 分钟也就是 12 小时。
答:这三辆汽车至少要720分钟(12小时)才能同时回到出发地。
例3:—盒围棋子,4个4个地数多1个,5个5个地数多1个,6个6个地数还多1个,又知棋子总数在150到200之间,求这盒棋子的总数。
如果从总数中取出1个,余下的总数便是4,5, 6的公倍数。因为4,5,6的最小公倍数是60,又知棋子总数在150到200之间,符合条件的只有1个,即:60×3+1=181 (个)。
例4:用96朵红玫现花和72朵白玫瑰花做花束,已知每个花束里的红玫瑰花的朵数相同,自玫瑰花的朵数也相同。最多可以做多少个花束?每个花束里至少有多少朵花
要把96朵红玻瑰花和72朵白玫瑰花做成花束,且每束花里的红玻瑰花朵数相同,白玫瑰花朵数也相同,那么做成花束的个数一定是96和72 的公因数,又要求花束的个数最多,所以花束的个数应是96和72的最大公因数。
解:最多可以做多少个花束?(96,72)=24(个)
每个花束里有几朵红玫瑰花? 96÷24=4(朵)
每个花束里有几朵白玫瑰花? 72 ÷ 24=3(朵)
每个花束里至少有几朵花? 4+3=7(朵)
答:最多可以做24个花束,每个花束里至少有7朵花。
例5:为了响应“植树造林,绿化荒山”的号召,六(1)班同学在老师的带领下去山坡上种树,种完树后,老师让同学们数数一共种了多少棵树,结果大家发现: 2棵2棵地数还剩 1棵,3棵3棵地数还剩2棵,4棵4棵地数还剩3棵。5棵5棵地数还剩4棵。 6棵6棵地数还剩5棵, 7棵7棵地数正好数完。那么他们至少种了多少棵树?
由题可知,如果多种1棵,就可以同时被2,3, 4,5, 6 整除,但又必须考虑实际的数能被7整除。[2, 3,4,5,6]=60,60-1=59 不能被7整除,不符合题意;60×2=120, 120-1=119, 119 能被 7 整除,符合题意。所以至少种了 119 棵树。
例6:公路边上有一排电线杆,从头到尾共25根。每相邻两根电线杆间的距离原来都是45米,现在要改为60米,可以有几根电线杆不需要移动?
不需要移动的电线杆距第一根的距离一定既是45的倍数,又是60的倍数。要先求45和60的最小公倍数,以及这条公路的全长,再求可以有几根电线杆不需要移动。
解:从第一根起至少相隔多少米的一根电线杆不需要移动?
[45,60]=180(米)
公路全长多少米?45×(25-1)=1080(米)
可以有几根电线杆不需要移动?1080÷180+1=7(根)
答:可以有7 根电线杆不需要移动。
例7、今有梨320个、糖果240个、饼干200个,将这些东西分成相同的礼品包送给儿童,但包数要最多,则每包有多少个梨?有多少个糖果?有多少个饼干?
320、240和200的最大公因数是:40
梨:320÷40=8(个)
糖果:240÷40=6 (个)
饼干:200÷40=5(个)
答:每包有8个梨。有6个糖果。有5个饼干。
例8、一筐鸡蛋,3个3个数,最后多1个;5个5个数,最后多1个;6个6个数,最后也多1个。这些鸡蛋至少有多少个?
3、5和6的最小公倍数是:30
30+1=31(个)
答:这些鸡蛋至少有31个。
