高中数学人教A版(2019)选必修2 课时作业14 数列求和(一)(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)选必修2 课时作业14 数列求和(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-20 16:54:33 | ||
图片预览



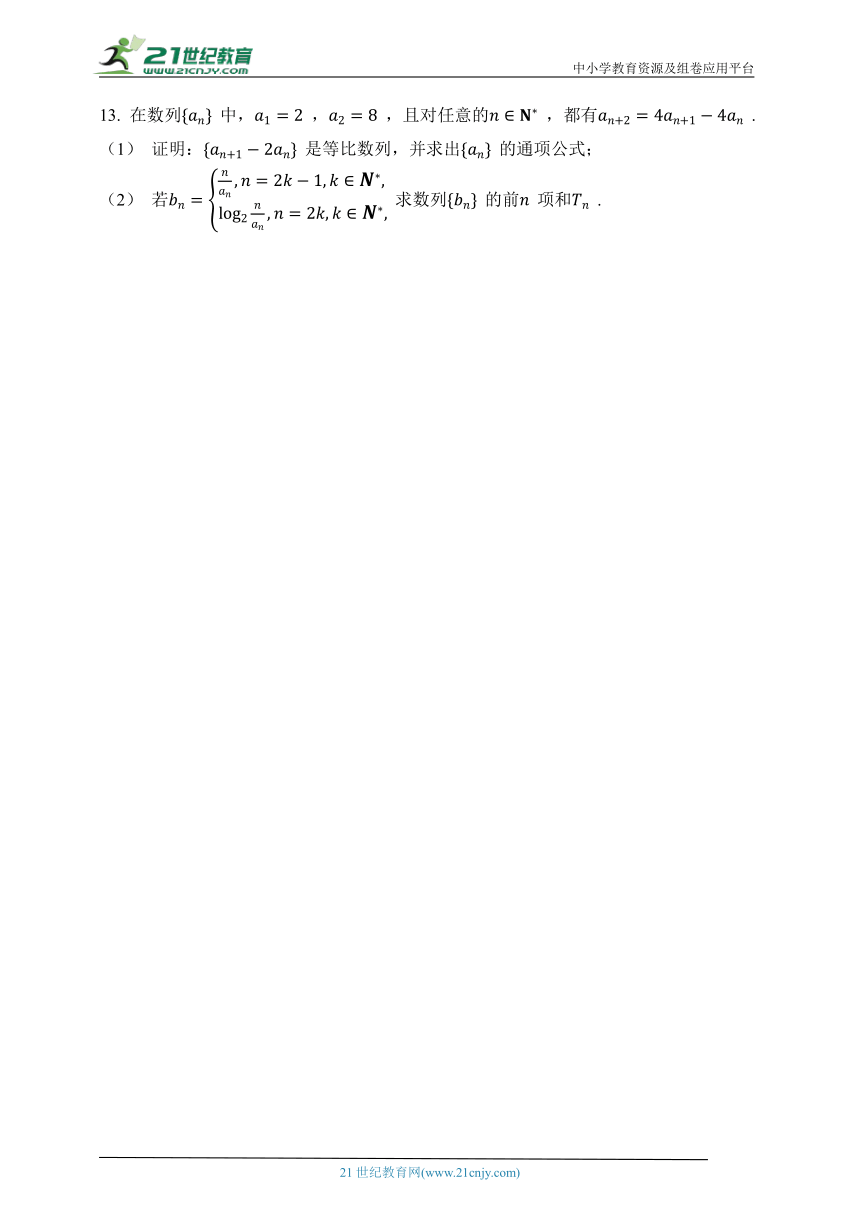

文档简介
中小学教育资源及组卷应用平台
课时作业14 数列求和(一)
基础达标练
1. 若数列 的通项公式为 ,则数列 的前 项和为( )
A. B.
C. D.
2. 已知数列 的通项公式是 ,则 ( )
A. B.
C. 3 033 D. 3 034
3. [2023福建莆田第六中学高二期中]已知等差数列 的前 项和为 ,且 , ,则 的前 项和 .
4. [2023湖北黄石二中高二期末]已知数列 满足 , ,且 , ,则该数列的前9项和为 .
5. [2023江西赣州高二月考]已知数列 的通项公式为 ,其前 项和为 ,则 .
6. [2023山东青岛高二期中]集合论是德国数学家康托尔于十九世纪末创立的,希尔伯特赞誉集合论“是数学天才最优秀的作品,是人类纯粹智力活动的最高成就之一”.取一条长度为1的线段,将它三等分,去掉中间一段,将留下的两段分别三等分,各去掉中间一段,留下更短的四段, ,将这样的操作一直继续下去,直至无穷.由于在不断分割舍弃过程中,所形成的线段的数目越来越多,长度越来越小,在极限情况下,得到一个离散的点集,称为康托尔三分集.若在前 次操作中总共去掉的线段长度之和不小于 ,则 的最小值为 .
(参考数据: , )
7. [2023湖南郴州高二期中]已知等差数列 的公差 ,前 项和为 ,且满足 .
(1) 若 , , 成等比数列,求 的值;
(2) 设 ,求数列 的前 项和 .
已知数列 满足 , ,求 的前 项和 .
素养提升练
9. [2023河北唐山一中高二期末](多选题)设首项为2的数列 的前 项和为 ,若 ,则下列结论正确的是( )
A. 数列 的通项公式为
B. 数列 的通项公式为
C. 数列 为等比数列
D. 数列 的前 项和为
10. [2023山西太原师范学院附属中学高二期末]高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设 ,用 表示不超过 的最大整数,则 称为高斯函数.已知数列 满足 ,且 ,若 ,数列 的前 项和为 ,则 ( )
A. 4 956 B. 4 959 C. 4 962 D. 4 965
11. (多选题)已知数列 满足 , ,且 , ,记 为数列 的前 项和,数列 是首项和公比都是2的等比数列,则使不等式 成立的整数 可以为( )
A. 7 B. 6 C. 5 D. 4
12. 已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,数列 的前 项和为 ,且满足 , .
(1) 求数列 的通项公式;
(2) 是否存在 ,使 ?若存在,求出所有符合条件的 的值;若不存在,请说明理由.
13. 在数列 中, , ,且对任意的 ,都有 .
(1) 证明: 是等比数列,并求出 的通项公式;
(2) 若 求数列 的前 项和 .
参考答案
基础达标练
1. 若数列 的通项公式为 ,则数列 的前 项和为( )
A. B. C. D.
【答案】D
【解析】由分组法求和,得数列 的前 项和 .
2. 已知数列 的通项公式是 ,则 ( )
A. B. C. 3 033 D. 3 034
【答案】 A
【解析】由 ,得 .
3. [2023福建莆田第六中学高二期中]已知等差数列 的前 项和为 ,且 , ,则 的前 项和 .
【答案】
【解析】设等差数列 的公差为 , , ,
解得
, ,
设 ,则 ,易知数列 是首项为 ,公差为 的等差数列,
则 .
4. [2023湖北黄石二中高二期末]已知数列 满足 , ,且 , ,则该数列的前9项和为 .
【答案】34
【解析】 , ,
当 为奇数时, , ;
当 为偶数时, ,则数列 是以 为首项,2为公差的等差数列.
.
5. [2023江西赣州高二月考]已知数列 的通项公式为 ,其前 项和为 ,则 .
【答案】
【解析】由题意得, , , , ,
又 的周期为4,
.
[2023山东青岛高二期中]集合论是德国数学家康托尔于十九世纪末创立的,希尔伯特赞誉集合论“是数学天才最优秀的作品,是人类纯粹智力活动的最高成就之一”.取一条长度为1的线段,将它三等分,去掉中间一段,将留下的两段分别三等分,各去掉中间一段,留下更短的四段, ,将这样的操作一直继续下去,直至无穷.由于在不断分割舍弃过程中,所形成的线段的数目越来越多,长度越来越小,在极限情况下,得到一个离散的点集,称为康托尔三分集.若在前 次操作中总共去掉的线段长度之和不小于 ,则 的最小值为 .
(参考数据: , )
【答案】 9
【解析】第一次操作去掉的线段长度为 ,
第二次操作去掉的线段长度之和为 ,
第三次操作去掉的线段长度之和为 , ,
第 次操作去掉的线段长度之和为 ,
由此可得去掉线段的总长度为 ,
令 ,得 ,得 ,
所以 ,所以 的最小值是9.
7. [2023湖南郴州高二期中]已知等差数列 的公差 ,前 项和为 ,且满足 .
(1) 若 , , 成等比数列,求 的值;
【解析】因为 ,所以 ,即 ,
解得 ,
所以 .
又 , , 成等比数列,所以 ,即 ,解得 .
(2) 设 ,求数列 的前 项和 .
【解析】因为 ,
所以
.
8. 已知数列 满足 , ,求 的前 项和 .
【解析】因为 , ,
所以 .
当 为偶数时, ;
当 为奇数时, .
综上所述,
素养提升练
9. [2023河北唐山一中高二期末](多选题)设首项为2的数列 的前 项和为 ,若 ,则下列结论正确的是( )
A. 数列 的通项公式为
B. 数列 的通项公式为
C. 数列 为等比数列
D. 数列 的前 项和为
【答案】 BD
【解析】因为 ,所以 ,
又 ,所以 ,所以 是以3为首项,3为公比的等比数列,所以 ,则 ,故 错误;
当 时, ,所以 ,当 时, 不满足上式,所以 故 正确;
由 可知, ,故 不是等比数列,故 错误;
因为 ,所以数列 的前 项和为 ,故 正确.
故选 .
10. [2023山西太原师范学院附属中学高二期末]高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设 ,用 表示不超过 的最大整数,则 称为高斯函数.已知数列 满足 ,且 ,若 ,数列 的前 项和为 ,则 ( )
A. 4 956 B. 4 959 C. 4 962 D. 4 965
【答案】 B
【解析】由 , ,由累加法可得:
,
所以 ,所以 .
当 时, ;当 时, ;
当 时, ;
当 时, .
因此 .故选 .
11. (多选题)已知数列 满足 , ,且 , ,记 为数列 的前 项和,数列 是首项和公比都是2的等比数列,则使不等式 成立的整数 可以为( )
A. 7 B. 6 C. 5 D. 4
【答案】ABC
【解析】由题意得,当 为偶数时, ,即 ,
所以 , , , 是以 为首项, 为公比的等比数列;当 为奇数时, ,所以 , , , 是以 为首项,2为公差的等差数列,
所以
,
因为数列 是首项和公比都是2的等比数列,
所以 , ,即 ,
依次检验:当 , , , 时,不满足题意,当 时,满足题意,所以满足条件的最小正整数为5,
故选 .
12. 已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,数列 的前 项和为 ,且满足 , .
(1) 求数列 的通项公式;
【解析】设等差数列的公差为 ,等比数列的公比为 ,
由
解得
所以
(2) 是否存在 ,使 ?若存在,求出所有符合条件的 的值;若不存在,请说明理由.
【解析】由(1)得,当 为偶数时, ;
当 为奇数时, .
当 为奇数时,由已知条件得, ,
化简得 ,解得 ;
当 为偶数时,由已知条件得, ,
化简得 ,解得 .
综上,存在 符合条件.
13. 在数列 中, , ,且对任意的 ,都有 .
(1) 证明: 是等比数列,并求出 的通项公式;
【解析】因为 ,所以 ,因为 , ,所以 ,
所以 ,所以 ,
所以 是以4为首项,2为公比的等比数列.
所以 ,所以 ,
又 ,所以 是以1为首项,1为公差的等差数列,
所以 ,所以 .
(2) 若 求数列 的前 项和 .
【解析】由(1)知
则数列 的奇数项是以 为首项, 为公比的等比数列;
偶数项是以 为首项, 为公差的等差数列.
所以当 为偶数,且 时,
;
当 为奇数,且 时,
.
又当 时, 满足上式,
所以当 为奇数,且 时, .
综上,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时作业14 数列求和(一)
基础达标练
1. 若数列 的通项公式为 ,则数列 的前 项和为( )
A. B.
C. D.
2. 已知数列 的通项公式是 ,则 ( )
A. B.
C. 3 033 D. 3 034
3. [2023福建莆田第六中学高二期中]已知等差数列 的前 项和为 ,且 , ,则 的前 项和 .
4. [2023湖北黄石二中高二期末]已知数列 满足 , ,且 , ,则该数列的前9项和为 .
5. [2023江西赣州高二月考]已知数列 的通项公式为 ,其前 项和为 ,则 .
6. [2023山东青岛高二期中]集合论是德国数学家康托尔于十九世纪末创立的,希尔伯特赞誉集合论“是数学天才最优秀的作品,是人类纯粹智力活动的最高成就之一”.取一条长度为1的线段,将它三等分,去掉中间一段,将留下的两段分别三等分,各去掉中间一段,留下更短的四段, ,将这样的操作一直继续下去,直至无穷.由于在不断分割舍弃过程中,所形成的线段的数目越来越多,长度越来越小,在极限情况下,得到一个离散的点集,称为康托尔三分集.若在前 次操作中总共去掉的线段长度之和不小于 ,则 的最小值为 .
(参考数据: , )
7. [2023湖南郴州高二期中]已知等差数列 的公差 ,前 项和为 ,且满足 .
(1) 若 , , 成等比数列,求 的值;
(2) 设 ,求数列 的前 项和 .
已知数列 满足 , ,求 的前 项和 .
素养提升练
9. [2023河北唐山一中高二期末](多选题)设首项为2的数列 的前 项和为 ,若 ,则下列结论正确的是( )
A. 数列 的通项公式为
B. 数列 的通项公式为
C. 数列 为等比数列
D. 数列 的前 项和为
10. [2023山西太原师范学院附属中学高二期末]高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设 ,用 表示不超过 的最大整数,则 称为高斯函数.已知数列 满足 ,且 ,若 ,数列 的前 项和为 ,则 ( )
A. 4 956 B. 4 959 C. 4 962 D. 4 965
11. (多选题)已知数列 满足 , ,且 , ,记 为数列 的前 项和,数列 是首项和公比都是2的等比数列,则使不等式 成立的整数 可以为( )
A. 7 B. 6 C. 5 D. 4
12. 已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,数列 的前 项和为 ,且满足 , .
(1) 求数列 的通项公式;
(2) 是否存在 ,使 ?若存在,求出所有符合条件的 的值;若不存在,请说明理由.
13. 在数列 中, , ,且对任意的 ,都有 .
(1) 证明: 是等比数列,并求出 的通项公式;
(2) 若 求数列 的前 项和 .
参考答案
基础达标练
1. 若数列 的通项公式为 ,则数列 的前 项和为( )
A. B. C. D.
【答案】D
【解析】由分组法求和,得数列 的前 项和 .
2. 已知数列 的通项公式是 ,则 ( )
A. B. C. 3 033 D. 3 034
【答案】 A
【解析】由 ,得 .
3. [2023福建莆田第六中学高二期中]已知等差数列 的前 项和为 ,且 , ,则 的前 项和 .
【答案】
【解析】设等差数列 的公差为 , , ,
解得
, ,
设 ,则 ,易知数列 是首项为 ,公差为 的等差数列,
则 .
4. [2023湖北黄石二中高二期末]已知数列 满足 , ,且 , ,则该数列的前9项和为 .
【答案】34
【解析】 , ,
当 为奇数时, , ;
当 为偶数时, ,则数列 是以 为首项,2为公差的等差数列.
.
5. [2023江西赣州高二月考]已知数列 的通项公式为 ,其前 项和为 ,则 .
【答案】
【解析】由题意得, , , , ,
又 的周期为4,
.
[2023山东青岛高二期中]集合论是德国数学家康托尔于十九世纪末创立的,希尔伯特赞誉集合论“是数学天才最优秀的作品,是人类纯粹智力活动的最高成就之一”.取一条长度为1的线段,将它三等分,去掉中间一段,将留下的两段分别三等分,各去掉中间一段,留下更短的四段, ,将这样的操作一直继续下去,直至无穷.由于在不断分割舍弃过程中,所形成的线段的数目越来越多,长度越来越小,在极限情况下,得到一个离散的点集,称为康托尔三分集.若在前 次操作中总共去掉的线段长度之和不小于 ,则 的最小值为 .
(参考数据: , )
【答案】 9
【解析】第一次操作去掉的线段长度为 ,
第二次操作去掉的线段长度之和为 ,
第三次操作去掉的线段长度之和为 , ,
第 次操作去掉的线段长度之和为 ,
由此可得去掉线段的总长度为 ,
令 ,得 ,得 ,
所以 ,所以 的最小值是9.
7. [2023湖南郴州高二期中]已知等差数列 的公差 ,前 项和为 ,且满足 .
(1) 若 , , 成等比数列,求 的值;
【解析】因为 ,所以 ,即 ,
解得 ,
所以 .
又 , , 成等比数列,所以 ,即 ,解得 .
(2) 设 ,求数列 的前 项和 .
【解析】因为 ,
所以
.
8. 已知数列 满足 , ,求 的前 项和 .
【解析】因为 , ,
所以 .
当 为偶数时, ;
当 为奇数时, .
综上所述,
素养提升练
9. [2023河北唐山一中高二期末](多选题)设首项为2的数列 的前 项和为 ,若 ,则下列结论正确的是( )
A. 数列 的通项公式为
B. 数列 的通项公式为
C. 数列 为等比数列
D. 数列 的前 项和为
【答案】 BD
【解析】因为 ,所以 ,
又 ,所以 ,所以 是以3为首项,3为公比的等比数列,所以 ,则 ,故 错误;
当 时, ,所以 ,当 时, 不满足上式,所以 故 正确;
由 可知, ,故 不是等比数列,故 错误;
因为 ,所以数列 的前 项和为 ,故 正确.
故选 .
10. [2023山西太原师范学院附属中学高二期末]高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设 ,用 表示不超过 的最大整数,则 称为高斯函数.已知数列 满足 ,且 ,若 ,数列 的前 项和为 ,则 ( )
A. 4 956 B. 4 959 C. 4 962 D. 4 965
【答案】 B
【解析】由 , ,由累加法可得:
,
所以 ,所以 .
当 时, ;当 时, ;
当 时, ;
当 时, .
因此 .故选 .
11. (多选题)已知数列 满足 , ,且 , ,记 为数列 的前 项和,数列 是首项和公比都是2的等比数列,则使不等式 成立的整数 可以为( )
A. 7 B. 6 C. 5 D. 4
【答案】ABC
【解析】由题意得,当 为偶数时, ,即 ,
所以 , , , 是以 为首项, 为公比的等比数列;当 为奇数时, ,所以 , , , 是以 为首项,2为公差的等差数列,
所以
,
因为数列 是首项和公比都是2的等比数列,
所以 , ,即 ,
依次检验:当 , , , 时,不满足题意,当 时,满足题意,所以满足条件的最小正整数为5,
故选 .
12. 已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,数列 的前 项和为 ,且满足 , .
(1) 求数列 的通项公式;
【解析】设等差数列的公差为 ,等比数列的公比为 ,
由
解得
所以
(2) 是否存在 ,使 ?若存在,求出所有符合条件的 的值;若不存在,请说明理由.
【解析】由(1)得,当 为偶数时, ;
当 为奇数时, .
当 为奇数时,由已知条件得, ,
化简得 ,解得 ;
当 为偶数时,由已知条件得, ,
化简得 ,解得 .
综上,存在 符合条件.
13. 在数列 中, , ,且对任意的 ,都有 .
(1) 证明: 是等比数列,并求出 的通项公式;
【解析】因为 ,所以 ,因为 , ,所以 ,
所以 ,所以 ,
所以 是以4为首项,2为公比的等比数列.
所以 ,所以 ,
又 ,所以 是以1为首项,1为公差的等差数列,
所以 ,所以 .
(2) 若 求数列 的前 项和 .
【解析】由(1)知
则数列 的奇数项是以 为首项, 为公比的等比数列;
偶数项是以 为首项, 为公差的等差数列.
所以当 为偶数,且 时,
;
当 为奇数,且 时,
.
又当 时, 满足上式,
所以当 为奇数,且 时, .
综上,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
