高中数学人教A版(2019)选必修2 课时作业20 导数的几何意义(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)选必修2 课时作业20 导数的几何意义(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 407.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-20 16:57:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
课时作业20 导数的几何意义
基础达标练
题组一 导数的几何意义的理解
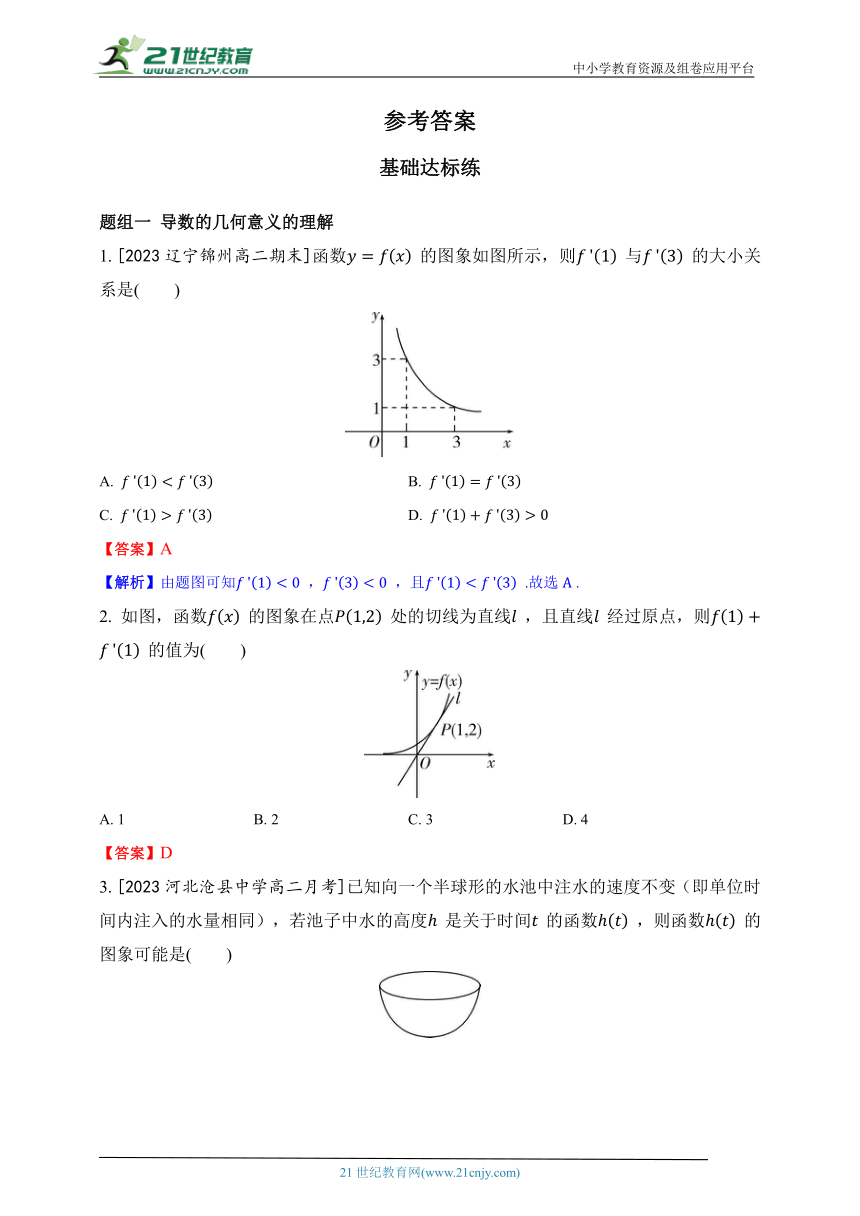
1. [2023辽宁锦州高二期末]函数 的图象如图所示,则 与 的大小关系是( )
A. B.
C. D.
2. 如图,函数 的图象在点 处的切线为直线 ,且直线 经过原点,则 的值为( )
A. 1 B. 2 C. 3 D. 4
3. [2023河北沧县中学高二月考]已知向一个半球形的水池中注水的速度不变(即单位时间内注入的水量相同),若池子中水的高度 是关于时间 的函数 ,则函数 的图象可能是( )
A. B.
C. D.
4. (多选题)下列说法正确的是( )
A. 若 不存在,则曲线 在点 处也可能有切线
B. 若曲线 在点 处有切线,则 必存在
C. 若 不存在,则曲线 在点 处的切线斜率不存在
D. 若曲线 在点 处没有切线,则 有可能存在
题组二 求切线方程(斜率)或切点坐标
5. 曲线 在点 处的切线的倾斜角为( )
A. B. C. D.
6. 过点 的直线与函数 的图象相切于点 ,则 .
7. 曲线 在点 处的切线方程为 .
题组三 导函数的计算及简单应用
8. 若 ,则 的导函数 ( )
A. B. C. D.
9. 已知函数 的图象如图所示,则其导函数图象的大致形状为 ( )
A. B. C. D.
10. 已知 ,则 .
素养提升练
11. (多选题)已知函数 的图象如图所示, 是 的导函数,则下列数值的排序正确的是( )
A.
B.
C.
D.
12. [2023山东青岛高二期中]若定义在 上的函数 满足 ,其导函数 满足 ,则 与 的大小关系一定是( )
A.
B.
C.
D.
13. 已知的图象在处的切线斜率为,则的值为 .
14. 设函数 ,若曲线 的斜率最小的切线与直线 平行,求 的值.
创新拓展练
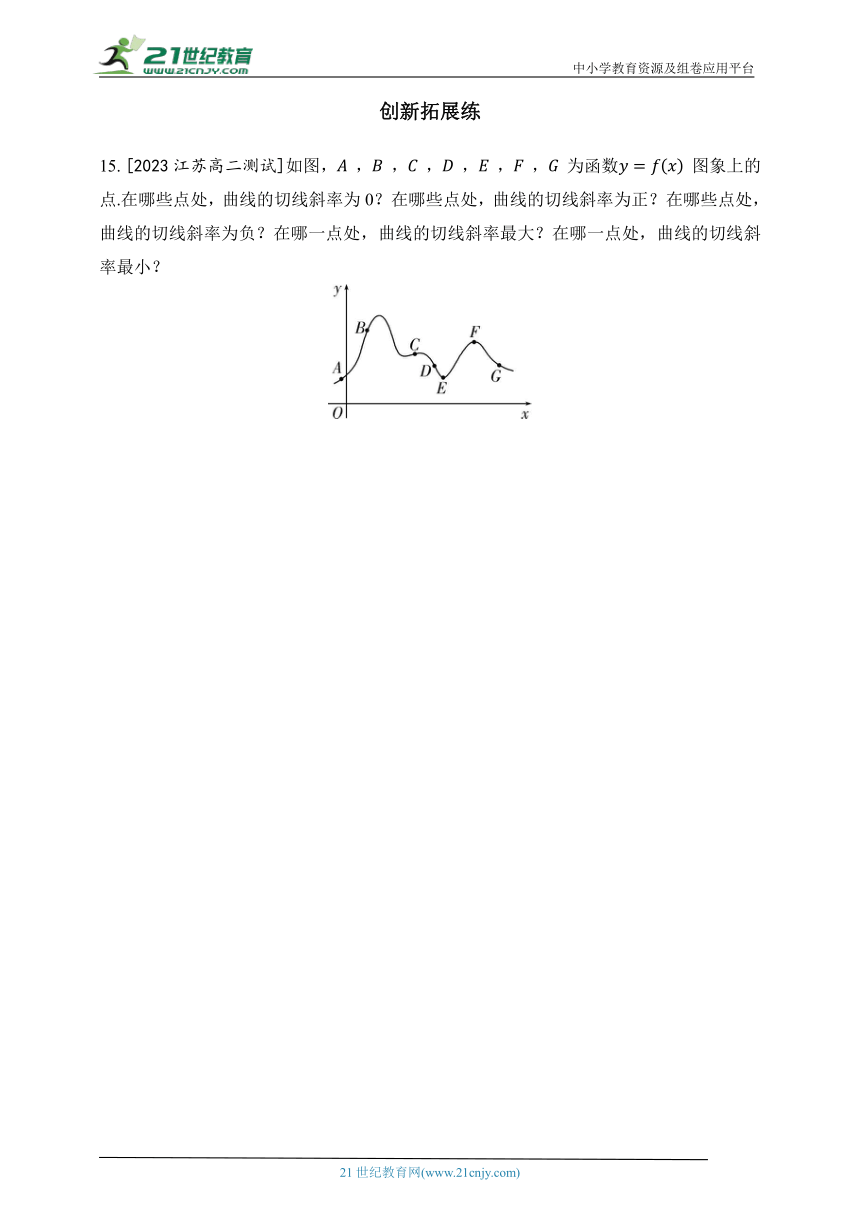
15. [2023江苏高二测试]如图, , , , , , , 为函数 图象上的点.在哪些点处,曲线的切线斜率为0?在哪些点处,曲线的切线斜率为正?在哪些点处,曲线的切线斜率为负?在哪一点处,曲线的切线斜率最大?在哪一点处,曲线的切线斜率最小?
参考答案
基础达标练
题组一 导数的几何意义的理解
1. [2023辽宁锦州高二期末]函数 的图象如图所示,则 与 的大小关系是( )
A. B.
C. D.
【答案】A
【解析】由题图可知 , ,且 .故选 .
2. 如图,函数 的图象在点 处的切线为直线 ,且直线 经过原点,则 的值为( )
A. 1 B. 2 C. 3 D. 4
【答案】D
3. [2023河北沧县中学高二月考]已知向一个半球形的水池中注水的速度不变(即单位时间内注入的水量相同),若池子中水的高度 是关于时间 的函数 ,则函数 的图象可能是( )
A. B.
C. D.
【答案】B
【解析】几何体为半球形,上面宽下面窄,相同的时间内注水量相同,所以高度增加得越来越慢,即图象越来越平缓,故选 .
4. (多选题)下列说法正确的是( )
A. 若 不存在,则曲线 在点 处也可能有切线
B. 若曲线 在点 处有切线,则 必存在
C. 若 不存在,则曲线 在点 处的切线斜率不存在
D. 若曲线 在点 处没有切线,则 有可能存在
【答案】AC
【解析】 , 不存在只能说明曲线在该点处的切线斜率不存在;
当斜率不存在时,切线也可能存在,其切线方程为 ,故 , 中的说法正确.
题组二 求切线方程(斜率)或切点坐标
5. 曲线 在点 处的切线的倾斜角为( )
A. B. C. D.
【答案】A
【解析】 ,
所以曲线 在点 处的切线的斜率为 ,
故曲线 在点 处的切线的倾斜角为 .
6. 过点 的直线与函数 的图象相切于点 ,则 .
【答案】0或
【解析】由题意得直线 的斜率
,
即 ,解得 或 .
7. 曲线 在点 处的切线方程为 .
【答案】
【解析】因为 ,所以 ,
故曲线 在点 处的切线斜率为 ,
故所求切线方程为 ,即 .
题组三 导函数的计算及简单应用
8. 若 ,则 的导函数 ( )
A. B. C. D.
【答案】C
9. 已知函数 的图象如图所示,则其导函数图象的大致形状为 ( )
A. B. C. D.
【答案】 A
【解析】由 的图象可知,函数 的图象在各点处的切线的斜率先正,后0,再正,由导数的几何意义可知, 的函数值先正,后0,再正,故只有选项 符合题意.
10. 已知 ,则 .
【答案】
【解析】
.
素养提升练
11. (多选题)已知函数 的图象如图所示, 是 的导函数,则下列数值的排序正确的是( )
A. B.
C. D.
【答案】AB
【解析】由函数的图象可知函数 是单调递增的,所以函数图象上任意一点处的导函数值都大于零,并且由图象可知,函数图象在 处的切线斜率 大于在 处的切线斜率 ,所以 , 正确;记 , ,作直线 ,则直线 的斜率 ,由函数图象可知, ,即 , 正确, 、 错误.故选 .
12. [2023山东青岛高二期中]若定义在 上的函数 满足 ,其导函数 满足 ,则 与 的大小关系一定是( )
A. B.
C. D.
【答案】 C
【解析】 ,且 ,
,即 .令 ,得 , ,
.故选 .
13. 已知的图象在处的切线斜率为,则的值为 .
【答案】 4
【解析】 ,
则 ,解得 .
14. 设函数 ,若曲线 的斜率最小的切线与直线 平行,求 的值.
【解析】由题意,函数 ,
则 ,
因为曲线 的斜率最小的切线与直线 平行,
所以 ,解得 ,因为 ,所以 .
创新拓展练
15. [2023江苏高二测试]如图, , , , , , , 为函数 图象上的点.在哪些点处,曲线的切线斜率为0?在哪些点处,曲线的切线斜率为正?在哪些点处,曲线的切线斜率为负?在哪一点处,曲线的切线斜率最大?在哪一点处,曲线的切线斜率最小?
【解析】根据导数的几何意义及函数的图象可知,
在 , 处的曲线的切线的斜率是0,
在 , , 处的曲线的切线的斜率是正,
在 , 处的曲线的切线的斜率是负,
在 处的曲线的切线的斜率最大,在 处的曲线的切线的斜率最小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时作业20 导数的几何意义
基础达标练
题组一 导数的几何意义的理解
1. [2023辽宁锦州高二期末]函数 的图象如图所示,则 与 的大小关系是( )
A. B.
C. D.
2. 如图,函数 的图象在点 处的切线为直线 ,且直线 经过原点,则 的值为( )
A. 1 B. 2 C. 3 D. 4
3. [2023河北沧县中学高二月考]已知向一个半球形的水池中注水的速度不变(即单位时间内注入的水量相同),若池子中水的高度 是关于时间 的函数 ,则函数 的图象可能是( )
A. B.
C. D.
4. (多选题)下列说法正确的是( )
A. 若 不存在,则曲线 在点 处也可能有切线
B. 若曲线 在点 处有切线,则 必存在
C. 若 不存在,则曲线 在点 处的切线斜率不存在
D. 若曲线 在点 处没有切线,则 有可能存在
题组二 求切线方程(斜率)或切点坐标
5. 曲线 在点 处的切线的倾斜角为( )
A. B. C. D.
6. 过点 的直线与函数 的图象相切于点 ,则 .
7. 曲线 在点 处的切线方程为 .
题组三 导函数的计算及简单应用
8. 若 ,则 的导函数 ( )
A. B. C. D.
9. 已知函数 的图象如图所示,则其导函数图象的大致形状为 ( )
A. B. C. D.
10. 已知 ,则 .
素养提升练
11. (多选题)已知函数 的图象如图所示, 是 的导函数,则下列数值的排序正确的是( )
A.
B.
C.
D.
12. [2023山东青岛高二期中]若定义在 上的函数 满足 ,其导函数 满足 ,则 与 的大小关系一定是( )
A.
B.
C.
D.
13. 已知的图象在处的切线斜率为,则的值为 .
14. 设函数 ,若曲线 的斜率最小的切线与直线 平行,求 的值.
创新拓展练
15. [2023江苏高二测试]如图, , , , , , , 为函数 图象上的点.在哪些点处,曲线的切线斜率为0?在哪些点处,曲线的切线斜率为正?在哪些点处,曲线的切线斜率为负?在哪一点处,曲线的切线斜率最大?在哪一点处,曲线的切线斜率最小?
参考答案
基础达标练
题组一 导数的几何意义的理解
1. [2023辽宁锦州高二期末]函数 的图象如图所示,则 与 的大小关系是( )
A. B.
C. D.
【答案】A
【解析】由题图可知 , ,且 .故选 .
2. 如图,函数 的图象在点 处的切线为直线 ,且直线 经过原点,则 的值为( )
A. 1 B. 2 C. 3 D. 4
【答案】D
3. [2023河北沧县中学高二月考]已知向一个半球形的水池中注水的速度不变(即单位时间内注入的水量相同),若池子中水的高度 是关于时间 的函数 ,则函数 的图象可能是( )
A. B.
C. D.
【答案】B
【解析】几何体为半球形,上面宽下面窄,相同的时间内注水量相同,所以高度增加得越来越慢,即图象越来越平缓,故选 .
4. (多选题)下列说法正确的是( )
A. 若 不存在,则曲线 在点 处也可能有切线
B. 若曲线 在点 处有切线,则 必存在
C. 若 不存在,则曲线 在点 处的切线斜率不存在
D. 若曲线 在点 处没有切线,则 有可能存在
【答案】AC
【解析】 , 不存在只能说明曲线在该点处的切线斜率不存在;
当斜率不存在时,切线也可能存在,其切线方程为 ,故 , 中的说法正确.
题组二 求切线方程(斜率)或切点坐标
5. 曲线 在点 处的切线的倾斜角为( )
A. B. C. D.
【答案】A
【解析】 ,
所以曲线 在点 处的切线的斜率为 ,
故曲线 在点 处的切线的倾斜角为 .
6. 过点 的直线与函数 的图象相切于点 ,则 .
【答案】0或
【解析】由题意得直线 的斜率
,
即 ,解得 或 .
7. 曲线 在点 处的切线方程为 .
【答案】
【解析】因为 ,所以 ,
故曲线 在点 处的切线斜率为 ,
故所求切线方程为 ,即 .
题组三 导函数的计算及简单应用
8. 若 ,则 的导函数 ( )
A. B. C. D.
【答案】C
9. 已知函数 的图象如图所示,则其导函数图象的大致形状为 ( )
A. B. C. D.
【答案】 A
【解析】由 的图象可知,函数 的图象在各点处的切线的斜率先正,后0,再正,由导数的几何意义可知, 的函数值先正,后0,再正,故只有选项 符合题意.
10. 已知 ,则 .
【答案】
【解析】
.
素养提升练
11. (多选题)已知函数 的图象如图所示, 是 的导函数,则下列数值的排序正确的是( )
A. B.
C. D.
【答案】AB
【解析】由函数的图象可知函数 是单调递增的,所以函数图象上任意一点处的导函数值都大于零,并且由图象可知,函数图象在 处的切线斜率 大于在 处的切线斜率 ,所以 , 正确;记 , ,作直线 ,则直线 的斜率 ,由函数图象可知, ,即 , 正确, 、 错误.故选 .
12. [2023山东青岛高二期中]若定义在 上的函数 满足 ,其导函数 满足 ,则 与 的大小关系一定是( )
A. B.
C. D.
【答案】 C
【解析】 ,且 ,
,即 .令 ,得 , ,
.故选 .
13. 已知的图象在处的切线斜率为,则的值为 .
【答案】 4
【解析】 ,
则 ,解得 .
14. 设函数 ,若曲线 的斜率最小的切线与直线 平行,求 的值.
【解析】由题意,函数 ,
则 ,
因为曲线 的斜率最小的切线与直线 平行,
所以 ,解得 ,因为 ,所以 .
创新拓展练
15. [2023江苏高二测试]如图, , , , , , , 为函数 图象上的点.在哪些点处,曲线的切线斜率为0?在哪些点处,曲线的切线斜率为正?在哪些点处,曲线的切线斜率为负?在哪一点处,曲线的切线斜率最大?在哪一点处,曲线的切线斜率最小?
【解析】根据导数的几何意义及函数的图象可知,
在 , 处的曲线的切线的斜率是0,
在 , , 处的曲线的切线的斜率是正,
在 , 处的曲线的切线的斜率是负,
在 处的曲线的切线的斜率最大,在 处的曲线的切线的斜率最小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
