人教版小学数学五年级下册2.《因数和倍数的复习》课件(共22张PPT)
文档属性
| 名称 | 人教版小学数学五年级下册2.《因数和倍数的复习》课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 12:54:11 | ||
图片预览








文档简介
(共22张PPT)
因数和倍数的复习
最小公倍数
公因数
公倍数
因数和倍数
倍 数
因 数
最大公因数
质 数
互 质 数
合 数
质因数
分解质因数
含有因数2、3、5的数的特征
→
自然数
按是否是2的倍数
按因数的个数
奇数
偶数
1
合数
质数
一个数既是36的因数,又是6的倍数,这个数可能是几?
6、12、18、36。
36的倍数有:
72,108,···
36,
一个数的最小倍数和最大因数相等
36的因数有:1,2,3,4,6,9,12,18,36。
36
36
温馨提示:
奇数不一定都是质数。如:9 51
偶数不一定都是合数。如:2
质数也不一定是奇数。如:2
合数也不一定是偶数。如:9
找最大公因数
一、列举法:
1.先找几个数的( )。
2.找出几个数( )因数。
3.确定( )。
二、用倍数关系:
如果两个数是( )时,
( )是这两个数的最大公因数。
三、用互质数:
两个是( ),最大的公因数是( )。
四、用相邻两个自然数:
相邻两个自然数(0除外)的最大公因数是( )。
短除法
因数
公有的
最大公因数
倍数关系
较小的数
互质数时
1
1
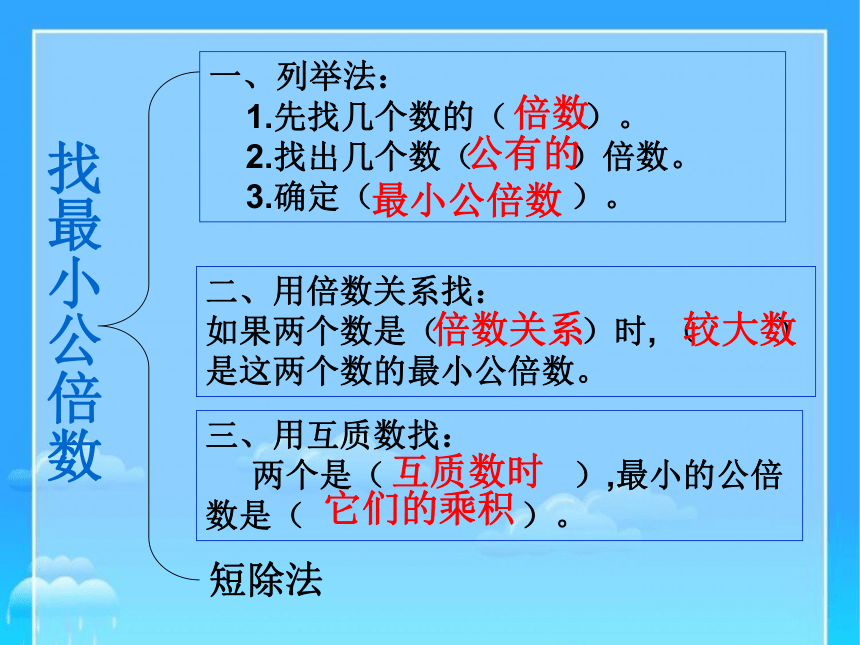
找最小公倍数
一、列举法:
1.先找几个数的( )。
2.找出几个数( )倍数。
3.确定( )。
二、用倍数关系找:
如果两个数是( )时, ( )
是这两个数的最小公倍数。
三、用互质数找:
两个是( ),最小的公倍数是( )。
短除法
倍数
公有的
最小公倍数
倍数关系
较大数
互质数时
它们的乘积
28和42的最大公因数是:
14
28
2
42
7
2 3
21
2×7×2×3=84
28和42的最小公倍数是:
2×7=14
根据上面的练习,想一想,利用短除法求两个数的最大公因数和最小公倍数,有什么相同点?有什么不同点?
观察:
14
28
2
42
7
2 3
21
求两个数的最大公因数 求两个数的最小公倍数
相同点
不同点
用短除法的形式分解质因数,直到商只有公因数1为止
把所有的除数连乘起来
把所有的除数和商连乘起来
求下列每组数的最大公因数和最小公倍数。
9和72
4和 5
16和24
(9、72)=9
9、72 =72
(4、5)=1
4、5 =20
(16、24)=8
16、24 =48
倍数关系
互质关系
一般关系
当两个数成倍数关系时,这两个数的最大公因数是较小数,最小公倍数是较大数.
当两个数只有公因数1时,这两个数的最大公因数是1,最小公倍数是这两个数的乘积.
求下列每组数的最大公因数和最小公倍数。
9和72
4和 5
16和24
(9、72)=9
9、72 =72
(4、5)=1
4、5 =20
(16、24)=8
16、24 =48
倍数关系
互质关系
一般关系
你能填吗?
(1)能同时被2、5、3整除的最小两位数是( ),最大两位数是( ),最小三位数是( ),最大的三位数( )。
(2)a÷b=7, a和b的最大公因数是( )最小公倍数是( )。
判断:
1、4.2÷0.6=7,我们说4.2是0.6的倍数。 ( )
2、两个质数相乘的积一定是合数。 ( )
3、是奇数又是合数且最小的是15。( )
猜年龄:
提示1: 老师的年龄十位上是质数中最小的奇数
提示2:我的年龄数是个奇数;
提示3:我的年龄数减去1就是5的倍数。
提示4:我的年龄数只有两个因数。
应用练习
1、小明给爸爸的工资存折设置了这样一个密码,
A B C D E F G H
A:是最小质数
B:既是奇数又是合数的一位数
C:是最小的自然数
D:只有因数1和7
E:是2和3的最小公倍数
F:最大的一位数
G:既不是质数也不是合数
H:最小的合数
师:你们能不能知道这个密码?
答案: 29076914
一个长方形周长是20,它的长和宽都是质数,那么这个长方形的长和宽分别是多少?
有块正方形布料,既可以都做成边长是8cm的方巾,也可以都做成边长是10cm的方巾,都没有剩余。这块布料的边长至少是( )cm。
实践运用
40
松花蛋的个数既是4的倍数,又是6的倍数。
而且松花蛋的个数在70~80之间。
如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇
8.
我跑一圈用
3 分钟。
我跑一圈用 4 分钟。
我要用
6 分钟。
此时爸爸、妈妈分别跑了多少圈
当堂检测
1) 用短除法求最大公因数和最小公倍数
20和32 24和30 64和48
2)一本书不论分给10人还是15人,正好分完,这本书至少多少本?
3)红花64朵,黄花48朵,用这两种花搭配成同样的花束,最多扎成多少束?
因数和倍数的复习
最小公倍数
公因数
公倍数
因数和倍数
倍 数
因 数
最大公因数
质 数
互 质 数
合 数
质因数
分解质因数
含有因数2、3、5的数的特征
→
自然数
按是否是2的倍数
按因数的个数
奇数
偶数
1
合数
质数
一个数既是36的因数,又是6的倍数,这个数可能是几?
6、12、18、36。
36的倍数有:
72,108,···
36,
一个数的最小倍数和最大因数相等
36的因数有:1,2,3,4,6,9,12,18,36。
36
36
温馨提示:
奇数不一定都是质数。如:9 51
偶数不一定都是合数。如:2
质数也不一定是奇数。如:2
合数也不一定是偶数。如:9
找最大公因数
一、列举法:
1.先找几个数的( )。
2.找出几个数( )因数。
3.确定( )。
二、用倍数关系:
如果两个数是( )时,
( )是这两个数的最大公因数。
三、用互质数:
两个是( ),最大的公因数是( )。
四、用相邻两个自然数:
相邻两个自然数(0除外)的最大公因数是( )。
短除法
因数
公有的
最大公因数
倍数关系
较小的数
互质数时
1
1
找最小公倍数
一、列举法:
1.先找几个数的( )。
2.找出几个数( )倍数。
3.确定( )。
二、用倍数关系找:
如果两个数是( )时, ( )
是这两个数的最小公倍数。
三、用互质数找:
两个是( ),最小的公倍数是( )。
短除法
倍数
公有的
最小公倍数
倍数关系
较大数
互质数时
它们的乘积
28和42的最大公因数是:
14
28
2
42
7
2 3
21
2×7×2×3=84
28和42的最小公倍数是:
2×7=14
根据上面的练习,想一想,利用短除法求两个数的最大公因数和最小公倍数,有什么相同点?有什么不同点?
观察:
14
28
2
42
7
2 3
21
求两个数的最大公因数 求两个数的最小公倍数
相同点
不同点
用短除法的形式分解质因数,直到商只有公因数1为止
把所有的除数连乘起来
把所有的除数和商连乘起来
求下列每组数的最大公因数和最小公倍数。
9和72
4和 5
16和24
(9、72)=9
9、72 =72
(4、5)=1
4、5 =20
(16、24)=8
16、24 =48
倍数关系
互质关系
一般关系
当两个数成倍数关系时,这两个数的最大公因数是较小数,最小公倍数是较大数.
当两个数只有公因数1时,这两个数的最大公因数是1,最小公倍数是这两个数的乘积.
求下列每组数的最大公因数和最小公倍数。
9和72
4和 5
16和24
(9、72)=9
9、72 =72
(4、5)=1
4、5 =20
(16、24)=8
16、24 =48
倍数关系
互质关系
一般关系
你能填吗?
(1)能同时被2、5、3整除的最小两位数是( ),最大两位数是( ),最小三位数是( ),最大的三位数( )。
(2)a÷b=7, a和b的最大公因数是( )最小公倍数是( )。
判断:
1、4.2÷0.6=7,我们说4.2是0.6的倍数。 ( )
2、两个质数相乘的积一定是合数。 ( )
3、是奇数又是合数且最小的是15。( )
猜年龄:
提示1: 老师的年龄十位上是质数中最小的奇数
提示2:我的年龄数是个奇数;
提示3:我的年龄数减去1就是5的倍数。
提示4:我的年龄数只有两个因数。
应用练习
1、小明给爸爸的工资存折设置了这样一个密码,
A B C D E F G H
A:是最小质数
B:既是奇数又是合数的一位数
C:是最小的自然数
D:只有因数1和7
E:是2和3的最小公倍数
F:最大的一位数
G:既不是质数也不是合数
H:最小的合数
师:你们能不能知道这个密码?
答案: 29076914
一个长方形周长是20,它的长和宽都是质数,那么这个长方形的长和宽分别是多少?
有块正方形布料,既可以都做成边长是8cm的方巾,也可以都做成边长是10cm的方巾,都没有剩余。这块布料的边长至少是( )cm。
实践运用
40
松花蛋的个数既是4的倍数,又是6的倍数。
而且松花蛋的个数在70~80之间。
如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇
8.
我跑一圈用
3 分钟。
我跑一圈用 4 分钟。
我要用
6 分钟。
此时爸爸、妈妈分别跑了多少圈
当堂检测
1) 用短除法求最大公因数和最小公倍数
20和32 24和30 64和48
2)一本书不论分给10人还是15人,正好分完,这本书至少多少本?
3)红花64朵,黄花48朵,用这两种花搭配成同样的花束,最多扎成多少束?
