课时作业(七) 平面向量基本定理(含解析)
文档属性
| 名称 | 课时作业(七) 平面向量基本定理(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 216.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览





文档简介
课时作业(七) 平面向量基本定理
基础达标
一、单项选择题
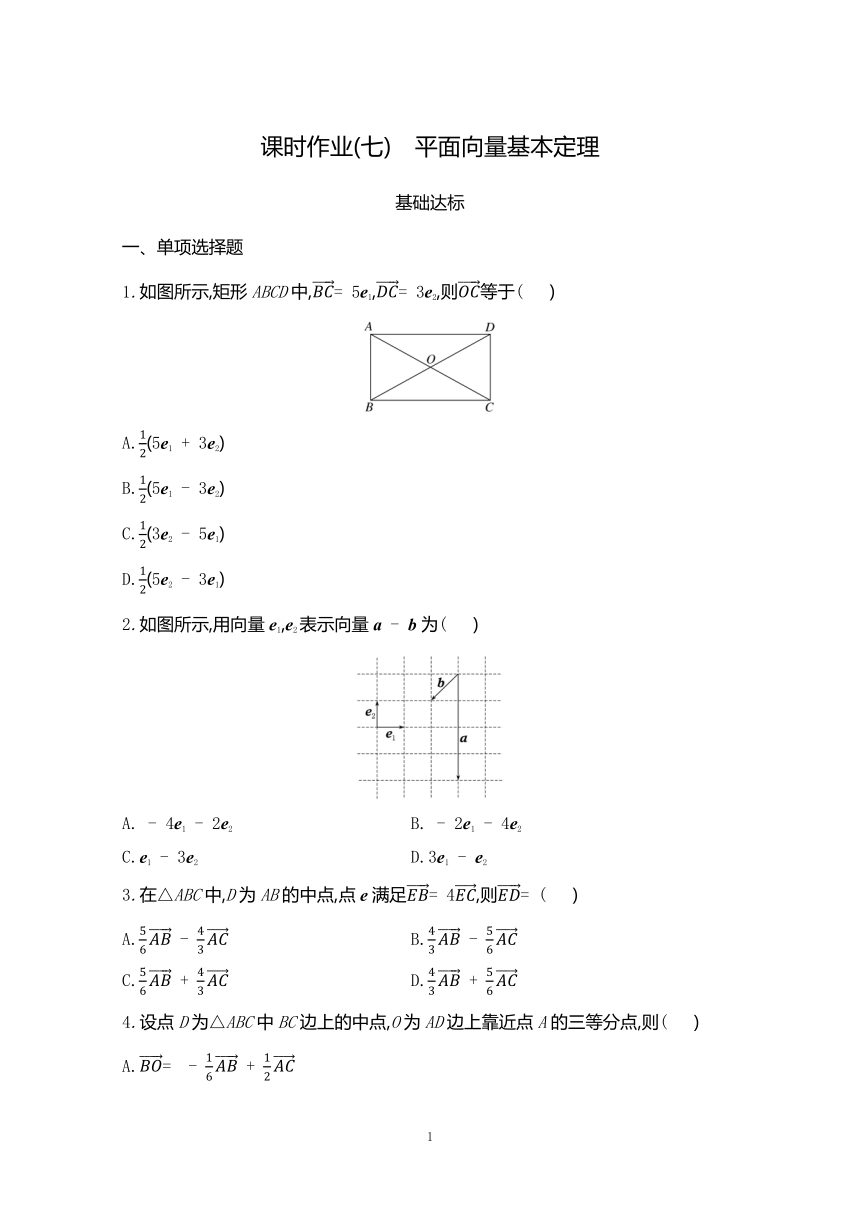
1.如图所示,矩形ABCD中,= 5e1,= 3e2,则等于( )
A.(5e1 + 3e2)
B.(5e1 - 3e2)
C.(3e2 - 5e1)
D.(5e2 - 3e1)
2.如图所示,用向量e1,e2表示向量a - b为( )
A. - 4e1 - 2e2 B. - 2e1 - 4e2
C.e1 - 3e2 D.3e1 - e2
3.在△ABC中,D为AB的中点,点e满足= 4,则= ( )
A. - B. -
C. + D. +
4.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则( )
A.= - +
B.= -
C.= -
D.= +
5.如图,在△ABC中,= ,P是BN上一点,若= t + ,则实数t的值为( )
A. B.
C. D.
6.如图,在△ABC中,AD⊥AB,= ,||= 1,则·= ( )
A.2 B.
C. D.
二、多项选择题
7.若{e1,e2}是平面内的一个基底,则下列四组向量中可以作为平面向量的基底的是( )
A.e1 - e2,e2 - e1 B.2e1 - e2,e1 - e2
C.2e2 - 3e1,6e1 - 3e2 D.e1 + e2,e1 + 3e2
8.D,e,F分别为△ABC的边BC,CA,AB的中点,且= a,= b,下列结论正确的是( )
A.= - a-b B.= a + b
C.= - a + b D.= a
三、填空题
9.向量a在基底{e1,e2}下可表示为a= 2e1 + 3e2,若a在基底{e1 + e2,e1 - e2}下可表示为a= λ(e1 + e2) + μ(e1 - e2),则λ= ,μ= 。
10.如图,在△MAB中,C是边AB上的一点,且AC= 5CB,设= a,= b,
则= 。(用a,b表示)
11.如图,在 ABCD中,e和F分别是边CD和BC的中点,若=λ+μ,
其中λ,μ∈R,则λ+μ= 。
四、解答题
12.如图,已知M,N,P是△ABC三边BC,CA,AB上的点,且= ,= ,= ,若= a,= b,试用基底{a,b}表示向量,。
13.如图,已知在梯形ABCD中,AD∥BC,e,F分别是AD,BC边上的中点,且BC= 3AD,= a,= b。试以{a,b}为基底表示,。
素养提升
14.如图,AB是☉O的直径,点C,D是半圆弧的两个三等分点,= a,= b,则等于( )
A.a - b
B.a - b
C.a + b
D.a + b
15.已知O是△ABC的重心,动点P满足= + + 2,则点P一定为( )
A.AB边中线的中点
B.AB边中线的三等分点(非重心)
C.△ABC的重心
D.AB边的中点
16.如图,平面内有三个向量,,,其中与的夹角为120°,与的夹角为30°,且||= ||= 1,||= 2,若=λ+μ(λ,μ∈R),则λ+μ的值为 。
参考答案
基础达标
一、单项选择题
1.如图所示,矩形ABCD中,= 5e1,= 3e2,则等于( )
A.(5e1 + 3e2)
B.(5e1 - 3e2)
C.(3e2 - 5e1)
D.(5e2 - 3e1)
【答案】A
【解析】= = ( - )= ( + )= (5e1 + 3e2)。
2.如图所示,用向量e1,e2表示向量a - b为( )
A. - 4e1 - 2e2 B. - 2e1 - 4e2
C.e1 - 3e2 D.3e1 - e2
【答案】C
3.在△ABC中,D为AB的中点,点e满足= 4,则= ( )
A. - B. -
C. + D. +
【答案】A
【解析】因为D为AB的中点,点e满足= 4,所以= ,= ,
所以= + = + = ( + ) - = - 。
4.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则( )
A.= - +
B.= -
C.= -
D.= +
【答案】D
【解析】依题意,得= - = - = ×( + ) - = - + 。故选D。
5.如图,在△ABC中,= ,P是BN上一点,若= t + ,则实数t的值为( )
A. B.
C. D.
【答案】C
【解析】解法一:因为= ,所以= 。
设= λ,则= + = + λ= + λ( + )
= + λ - + = λ + (1 - λ),
又= t + ,所以t + = λ + (1 - λ),
由与不共线,得解得t= λ= 。故选C。
解法二:因为= ,所以= ,所以= t + = t + 。
因为B,P,N三点共线,所以t + = 1,所以t= 。故选C。
6.如图,在△ABC中,AD⊥AB,= ,||= 1,则·= ( )
A.2 B.
C. D.
【答案】D
【解析】设{,}为基底,由题图可得·= (+)·= ·+·。
因为AD⊥AB,所以·= 0。
又因为= ,
所以·= ·= ( + )·= 0 + ||2= ,
所以·= 0 + = 。故选D。
二、多项选择题
7.若{e1,e2}是平面内的一个基底,则下列四组向量中可以作为平面向量的基底的是( )
A.e1 - e2,e2 - e1 B.2e1 - e2,e1 - e2
C.2e2 - 3e1,6e1 - 3e2 D.e1 + e2,e1 + 3e2
【答案】CD
【解析】选项A中,两个向量为相反向量,即e1-e2= -(e2-e1),则e1-e2, e2-e1为共线向量;
选项B中,2e1 - e2= 2,两向量也为共线向量;
选项C中,6e1 - 3e2≠ - 2(2e2 - 3e1),两向量为不共线向量。根据不共线的向量可以作为基底,知选项C,D中的两向量可作为基底。
8.D,e,F分别为△ABC的边BC,CA,AB的中点,且= a,= b,下列结论正确的是( )
A.= - a-b B.= a + b
C.= - a + b D.= a
【答案】ABC
【解析】如图,= + = - + = -b- a,A正确;
= + = a+b,B正确;
= + = -b- a,= + =b+ (-b - a)= b - a,C正确;
= = - a,D不正确。
三、填空题
9.向量a在基底{e1,e2}下可表示为a= 2e1 + 3e2,若a在基底{e1 + e2,e1 - e2}下可表示为a= λ(e1 + e2) + μ(e1 - e2),则λ= ,μ= 。
【答案】 ;-
【解析】由条件,可知解得
10.如图,在△MAB中,C是边AB上的一点,且AC= 5CB,设= a,= b,
则= 。(用a,b表示)
【答案】 a + b
【解析】= += += + (-)= += a+b。
11.如图,在 ABCD中,e和F分别是边CD和BC的中点,若=λ+μ,
其中λ,μ∈R,则λ+μ= 。
【答案】
【解析】设= a,= b,则= a +b,= a +b,
又因为= a +b=λ + μ= a + b,a与b不共线,
所以即λ= μ= ,所以λ+μ= 。
四、解答题
12.如图,已知M,N,P是△ABC三边BC,CA,AB上的点,且= ,= ,= ,若= a,= b,试用基底{a,b}表示向量,。
【解析】因为= ,所以= ,
所以= - = - = a - b,
= + = + = + ( - )
= + = a + b。
13.如图,已知在梯形ABCD中,AD∥BC,e,F分别是AD,BC边上的中点,且BC= 3AD,= a,= b。试以{a,b}为基底表示,。
【解析】如图,连接FA。
因为AD∥BC,且AD= BC,
所以= = b,
所以= = b。
因为= ,所以= b,
所以= - = a - b。
所以= + = - -
= - b - = b - a,
= + = - ( + )
= - = b - a。
素养提升
14.如图,AB是☉O的直径,点C,D是半圆弧的两个三等分点,= a,= b,则等于( )
A.a - b
B.a - b
C.a + b
D.a + b
【答案】D
【解析】连接CD,OD(图略),因为点C,D是半圆弧的两个三等分点,
所以= ,所以CD∥AB,∠CAD= ∠DAB= 30°,
因为OA= OD,所以∠ADO= ∠DAO= 30°,所以∠CAD= ∠ADO= 30°,
所以AC∥DO,所以四边形ACDO为平行四边形,= + 。
因为= = a,= b,所以= a + b。故选D。
15.已知O是△ABC的重心,动点P满足= + + 2,则点P一定为( )
A.AB边中线的中点
B.AB边中线的三等分点(非重心)
C.△ABC的重心
D.AB边的中点
【答案】B
【解析】O是△ABC的重心,所以 + + = 0,
所以= = ,
所以点P是线段OC的中点,即AB边中线的三等分点(非重心)。
16.如图,平面内有三个向量,,,其中与的夹角为120°,与的夹角为30°,且||= ||= 1,||= 2,若=λ+μ(λ,μ∈R),则λ+μ的值为 。
【答案】6
【解析】如图,作平行四边形ODCe,则= + 。
在Rt△OCD中,因为||= 2,∠COD= 30°,∠OCD= 90°,
所以||= 4,||= 2,故= 4,= 2,即λ= 4,μ= 2,所以λ + μ= 6。
基础达标
一、单项选择题
1.如图所示,矩形ABCD中,= 5e1,= 3e2,则等于( )
A.(5e1 + 3e2)
B.(5e1 - 3e2)
C.(3e2 - 5e1)
D.(5e2 - 3e1)
2.如图所示,用向量e1,e2表示向量a - b为( )
A. - 4e1 - 2e2 B. - 2e1 - 4e2
C.e1 - 3e2 D.3e1 - e2
3.在△ABC中,D为AB的中点,点e满足= 4,则= ( )
A. - B. -
C. + D. +
4.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则( )
A.= - +
B.= -
C.= -
D.= +
5.如图,在△ABC中,= ,P是BN上一点,若= t + ,则实数t的值为( )
A. B.
C. D.
6.如图,在△ABC中,AD⊥AB,= ,||= 1,则·= ( )
A.2 B.
C. D.
二、多项选择题
7.若{e1,e2}是平面内的一个基底,则下列四组向量中可以作为平面向量的基底的是( )
A.e1 - e2,e2 - e1 B.2e1 - e2,e1 - e2
C.2e2 - 3e1,6e1 - 3e2 D.e1 + e2,e1 + 3e2
8.D,e,F分别为△ABC的边BC,CA,AB的中点,且= a,= b,下列结论正确的是( )
A.= - a-b B.= a + b
C.= - a + b D.= a
三、填空题
9.向量a在基底{e1,e2}下可表示为a= 2e1 + 3e2,若a在基底{e1 + e2,e1 - e2}下可表示为a= λ(e1 + e2) + μ(e1 - e2),则λ= ,μ= 。
10.如图,在△MAB中,C是边AB上的一点,且AC= 5CB,设= a,= b,
则= 。(用a,b表示)
11.如图,在 ABCD中,e和F分别是边CD和BC的中点,若=λ+μ,
其中λ,μ∈R,则λ+μ= 。
四、解答题
12.如图,已知M,N,P是△ABC三边BC,CA,AB上的点,且= ,= ,= ,若= a,= b,试用基底{a,b}表示向量,。
13.如图,已知在梯形ABCD中,AD∥BC,e,F分别是AD,BC边上的中点,且BC= 3AD,= a,= b。试以{a,b}为基底表示,。
素养提升
14.如图,AB是☉O的直径,点C,D是半圆弧的两个三等分点,= a,= b,则等于( )
A.a - b
B.a - b
C.a + b
D.a + b
15.已知O是△ABC的重心,动点P满足= + + 2,则点P一定为( )
A.AB边中线的中点
B.AB边中线的三等分点(非重心)
C.△ABC的重心
D.AB边的中点
16.如图,平面内有三个向量,,,其中与的夹角为120°,与的夹角为30°,且||= ||= 1,||= 2,若=λ+μ(λ,μ∈R),则λ+μ的值为 。
参考答案
基础达标
一、单项选择题
1.如图所示,矩形ABCD中,= 5e1,= 3e2,则等于( )
A.(5e1 + 3e2)
B.(5e1 - 3e2)
C.(3e2 - 5e1)
D.(5e2 - 3e1)
【答案】A
【解析】= = ( - )= ( + )= (5e1 + 3e2)。
2.如图所示,用向量e1,e2表示向量a - b为( )
A. - 4e1 - 2e2 B. - 2e1 - 4e2
C.e1 - 3e2 D.3e1 - e2
【答案】C
3.在△ABC中,D为AB的中点,点e满足= 4,则= ( )
A. - B. -
C. + D. +
【答案】A
【解析】因为D为AB的中点,点e满足= 4,所以= ,= ,
所以= + = + = ( + ) - = - 。
4.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则( )
A.= - +
B.= -
C.= -
D.= +
【答案】D
【解析】依题意,得= - = - = ×( + ) - = - + 。故选D。
5.如图,在△ABC中,= ,P是BN上一点,若= t + ,则实数t的值为( )
A. B.
C. D.
【答案】C
【解析】解法一:因为= ,所以= 。
设= λ,则= + = + λ= + λ( + )
= + λ - + = λ + (1 - λ),
又= t + ,所以t + = λ + (1 - λ),
由与不共线,得解得t= λ= 。故选C。
解法二:因为= ,所以= ,所以= t + = t + 。
因为B,P,N三点共线,所以t + = 1,所以t= 。故选C。
6.如图,在△ABC中,AD⊥AB,= ,||= 1,则·= ( )
A.2 B.
C. D.
【答案】D
【解析】设{,}为基底,由题图可得·= (+)·= ·+·。
因为AD⊥AB,所以·= 0。
又因为= ,
所以·= ·= ( + )·= 0 + ||2= ,
所以·= 0 + = 。故选D。
二、多项选择题
7.若{e1,e2}是平面内的一个基底,则下列四组向量中可以作为平面向量的基底的是( )
A.e1 - e2,e2 - e1 B.2e1 - e2,e1 - e2
C.2e2 - 3e1,6e1 - 3e2 D.e1 + e2,e1 + 3e2
【答案】CD
【解析】选项A中,两个向量为相反向量,即e1-e2= -(e2-e1),则e1-e2, e2-e1为共线向量;
选项B中,2e1 - e2= 2,两向量也为共线向量;
选项C中,6e1 - 3e2≠ - 2(2e2 - 3e1),两向量为不共线向量。根据不共线的向量可以作为基底,知选项C,D中的两向量可作为基底。
8.D,e,F分别为△ABC的边BC,CA,AB的中点,且= a,= b,下列结论正确的是( )
A.= - a-b B.= a + b
C.= - a + b D.= a
【答案】ABC
【解析】如图,= + = - + = -b- a,A正确;
= + = a+b,B正确;
= + = -b- a,= + =b+ (-b - a)= b - a,C正确;
= = - a,D不正确。
三、填空题
9.向量a在基底{e1,e2}下可表示为a= 2e1 + 3e2,若a在基底{e1 + e2,e1 - e2}下可表示为a= λ(e1 + e2) + μ(e1 - e2),则λ= ,μ= 。
【答案】 ;-
【解析】由条件,可知解得
10.如图,在△MAB中,C是边AB上的一点,且AC= 5CB,设= a,= b,
则= 。(用a,b表示)
【答案】 a + b
【解析】= += += + (-)= += a+b。
11.如图,在 ABCD中,e和F分别是边CD和BC的中点,若=λ+μ,
其中λ,μ∈R,则λ+μ= 。
【答案】
【解析】设= a,= b,则= a +b,= a +b,
又因为= a +b=λ + μ= a + b,a与b不共线,
所以即λ= μ= ,所以λ+μ= 。
四、解答题
12.如图,已知M,N,P是△ABC三边BC,CA,AB上的点,且= ,= ,= ,若= a,= b,试用基底{a,b}表示向量,。
【解析】因为= ,所以= ,
所以= - = - = a - b,
= + = + = + ( - )
= + = a + b。
13.如图,已知在梯形ABCD中,AD∥BC,e,F分别是AD,BC边上的中点,且BC= 3AD,= a,= b。试以{a,b}为基底表示,。
【解析】如图,连接FA。
因为AD∥BC,且AD= BC,
所以= = b,
所以= = b。
因为= ,所以= b,
所以= - = a - b。
所以= + = - -
= - b - = b - a,
= + = - ( + )
= - = b - a。
素养提升
14.如图,AB是☉O的直径,点C,D是半圆弧的两个三等分点,= a,= b,则等于( )
A.a - b
B.a - b
C.a + b
D.a + b
【答案】D
【解析】连接CD,OD(图略),因为点C,D是半圆弧的两个三等分点,
所以= ,所以CD∥AB,∠CAD= ∠DAB= 30°,
因为OA= OD,所以∠ADO= ∠DAO= 30°,所以∠CAD= ∠ADO= 30°,
所以AC∥DO,所以四边形ACDO为平行四边形,= + 。
因为= = a,= b,所以= a + b。故选D。
15.已知O是△ABC的重心,动点P满足= + + 2,则点P一定为( )
A.AB边中线的中点
B.AB边中线的三等分点(非重心)
C.△ABC的重心
D.AB边的中点
【答案】B
【解析】O是△ABC的重心,所以 + + = 0,
所以= = ,
所以点P是线段OC的中点,即AB边中线的三等分点(非重心)。
16.如图,平面内有三个向量,,,其中与的夹角为120°,与的夹角为30°,且||= ||= 1,||= 2,若=λ+μ(λ,μ∈R),则λ+μ的值为 。
【答案】6
【解析】如图,作平行四边形ODCe,则= + 。
在Rt△OCD中,因为||= 2,∠COD= 30°,∠OCD= 90°,
所以||= 4,||= 2,故= 4,= 2,即λ= 4,μ= 2,所以λ + μ= 6。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
