河北省衡水市武强中学2023-2024学年高一下学期期中考试数学试题(含答案)
文档属性
| 名称 | 河北省衡水市武强中学2023-2024学年高一下学期期中考试数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览



文档简介
武强中学2023-2024学年高一下学期期中考试
数学试题
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
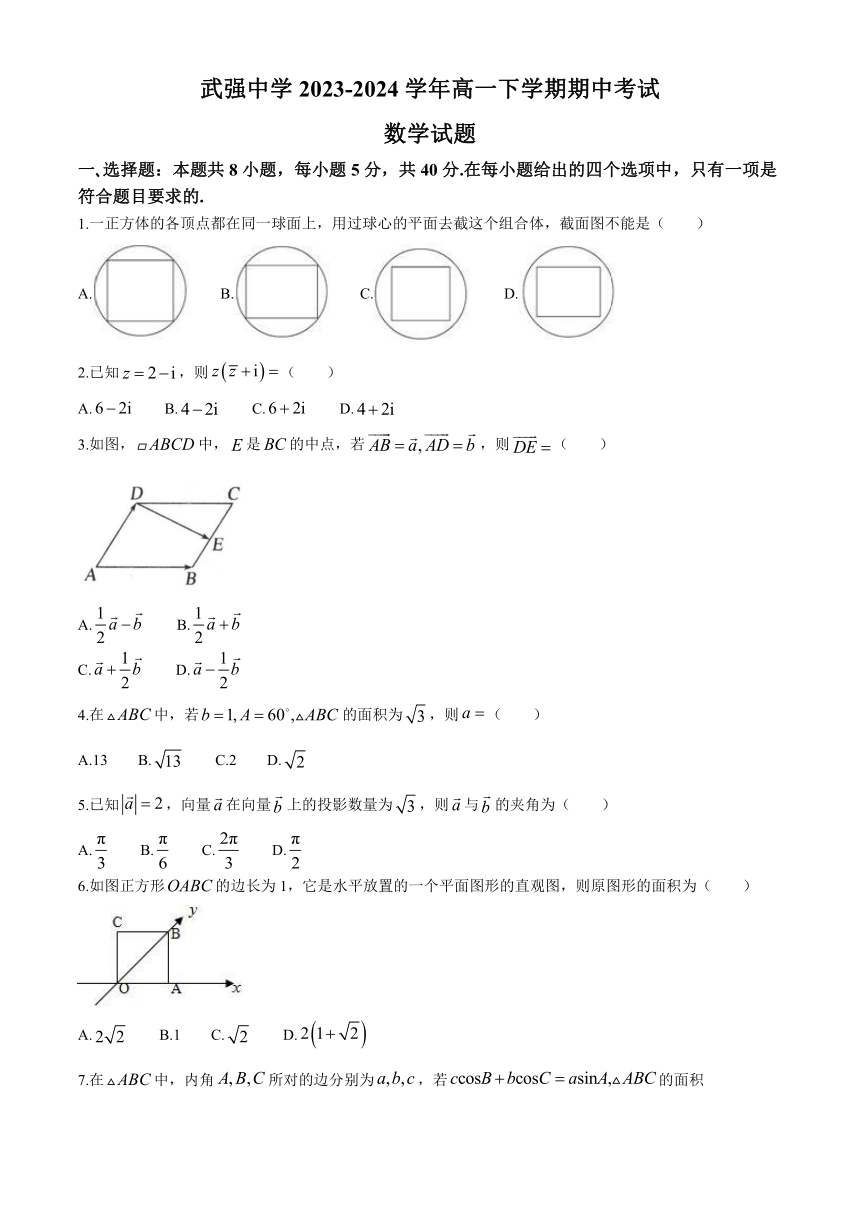
1.一正方体的各顶点都在同一球面上,用过球心的平面去截这个组合体,截面图不能是( )
A. B. C. D.
2.已知,则( )
A. B. C. D.
3.如图,中,是的中点,若,则( )
A. B.
C. D.
4.在中,若的面积为,则( )
A.13 B. C.2 D.
5.已知,向量在向量上的投影数量为,则与的夹角为( )
A. B. C. D.
6.如图正方形的边长为1,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
A. B.1 C. D.
7.在中,内角所对的边分别为,若的面积,则( )
A. B. C. D.
8.已知是边长为2的等边三角形,为平面内一点,则的最小值是( )
A.-2 B. C. D.-1
二 多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数为的共轭复数,复数,则下列结论正确的是( )
A.对应的点在复平面的第二象限 B.
C.的实部为 D.的虚部为
10.如果平面向量,那么下列结论中正确的是( )
A.
B.
C.与的夹角为
D.在方向上的投影向量为
11.在中,下列命题正确的是( )
A.若,则
B.若,则定为等腰三角形
C.若,则定为直角三角形
D.若三角形的三边的比是,则此三角形的最大角为钝角
三 填空题:本题共3小题,每小题5分,共15分.
12.的内角的对边分别为,已知,则__________.
13.水平放置的的斜二测直观图如图所示,已知,则边上的中线的实际长度为__________.
14.如图,在同一个平面内,向量的模分别为与的夹角为,且与的夹角为.若,则__________.
四 解答题:本题共5小题,共77分.解答应写出文字说明 证明过程或演算步骤.
15.(本小题13分)
已知.
(1)求向量与的夹角;
(2)当向量与垂直时,求实数的值.
16.(本小题15分)
已知:复数,其中为虚数单位.
(1)求及;
(2)若,求实数的值.
17.(本小题15分)
的内角所对边分别为,已知.
(1)求;
(2)若,求的面积.
18.(本小题17分)
已知复数(是虚数单位,),且为纯虚数(是的共轭复数)
(1)求实数及;
(2)设复数,且复数对应的点在第二象限,求实数的取值范围.
19.(本小题17分)
在中,角所对边分别为,现有下列四个条件:
①;②;③;④.
(1)③④两个条件可以同时成立吗?请说明理由;
(2)已知同时满足上述四个条件中的三个,请选择使有解的三个条件,求的面积.
注:如果选择多个组合作为条件分别解答,按第一个解答计分.
高一数学参考答案
一 单项选择题:
1-8ACDB BADC
二 多项选择题:
9.BC 10.AB 11.ACD
三 填空题:
12.75° 13. 14.3
四 解答题:
15.解:(1),
.
,
;
(2)向量与垂直,,
,即,
解得.
16.解:(1),
.
(2)由得:
,即
所以,解之得.
17.解:(1)因为,根据正弦定理得,
又,从而,
由于,所以.
(2)根据余弦定理,而,
代入整理得,解得或(舍去).
故的面积为.
18.解:(1)因为,
,
又为纯虚数,,
;
(2),
因为复数所对应的点在第二象限,
,解得,
即实数的取值范围为.
19.解:(1)由条件③得,
解得或(舍),
因为,所以;
由条件④得,
因为,
而在单调递减,所以.
于是,与矛盾.所以中③④不能同时成立.
(2)因为同时满足上述四个条件中的三个,不能同时满足③④,则满足三角形有解的所有组合为①②③或①②.
若选择组合①②③:有,即,
因为,所以为直角三角形,所以,
所以的面积.
若选择组合①②④:
由,即,解得,
因为,所以,
所以的面积.
数学试题
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一正方体的各顶点都在同一球面上,用过球心的平面去截这个组合体,截面图不能是( )
A. B. C. D.
2.已知,则( )
A. B. C. D.
3.如图,中,是的中点,若,则( )
A. B.
C. D.
4.在中,若的面积为,则( )
A.13 B. C.2 D.
5.已知,向量在向量上的投影数量为,则与的夹角为( )
A. B. C. D.
6.如图正方形的边长为1,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
A. B.1 C. D.
7.在中,内角所对的边分别为,若的面积,则( )
A. B. C. D.
8.已知是边长为2的等边三角形,为平面内一点,则的最小值是( )
A.-2 B. C. D.-1
二 多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数为的共轭复数,复数,则下列结论正确的是( )
A.对应的点在复平面的第二象限 B.
C.的实部为 D.的虚部为
10.如果平面向量,那么下列结论中正确的是( )
A.
B.
C.与的夹角为
D.在方向上的投影向量为
11.在中,下列命题正确的是( )
A.若,则
B.若,则定为等腰三角形
C.若,则定为直角三角形
D.若三角形的三边的比是,则此三角形的最大角为钝角
三 填空题:本题共3小题,每小题5分,共15分.
12.的内角的对边分别为,已知,则__________.
13.水平放置的的斜二测直观图如图所示,已知,则边上的中线的实际长度为__________.
14.如图,在同一个平面内,向量的模分别为与的夹角为,且与的夹角为.若,则__________.
四 解答题:本题共5小题,共77分.解答应写出文字说明 证明过程或演算步骤.
15.(本小题13分)
已知.
(1)求向量与的夹角;
(2)当向量与垂直时,求实数的值.
16.(本小题15分)
已知:复数,其中为虚数单位.
(1)求及;
(2)若,求实数的值.
17.(本小题15分)
的内角所对边分别为,已知.
(1)求;
(2)若,求的面积.
18.(本小题17分)
已知复数(是虚数单位,),且为纯虚数(是的共轭复数)
(1)求实数及;
(2)设复数,且复数对应的点在第二象限,求实数的取值范围.
19.(本小题17分)
在中,角所对边分别为,现有下列四个条件:
①;②;③;④.
(1)③④两个条件可以同时成立吗?请说明理由;
(2)已知同时满足上述四个条件中的三个,请选择使有解的三个条件,求的面积.
注:如果选择多个组合作为条件分别解答,按第一个解答计分.
高一数学参考答案
一 单项选择题:
1-8ACDB BADC
二 多项选择题:
9.BC 10.AB 11.ACD
三 填空题:
12.75° 13. 14.3
四 解答题:
15.解:(1),
.
,
;
(2)向量与垂直,,
,即,
解得.
16.解:(1),
.
(2)由得:
,即
所以,解之得.
17.解:(1)因为,根据正弦定理得,
又,从而,
由于,所以.
(2)根据余弦定理,而,
代入整理得,解得或(舍去).
故的面积为.
18.解:(1)因为,
,
又为纯虚数,,
;
(2),
因为复数所对应的点在第二象限,
,解得,
即实数的取值范围为.
19.解:(1)由条件③得,
解得或(舍),
因为,所以;
由条件④得,
因为,
而在单调递减,所以.
于是,与矛盾.所以中③④不能同时成立.
(2)因为同时满足上述四个条件中的三个,不能同时满足③④,则满足三角形有解的所有组合为①②③或①②.
若选择组合①②③:有,即,
因为,所以为直角三角形,所以,
所以的面积.
若选择组合①②④:
由,即,解得,
因为,所以,
所以的面积.
同课章节目录
