2023-2024学年人教版八年级数学下册课件一次函数(54张PPT)
文档属性
| 名称 | 2023-2024学年人教版八年级数学下册课件一次函数(54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览






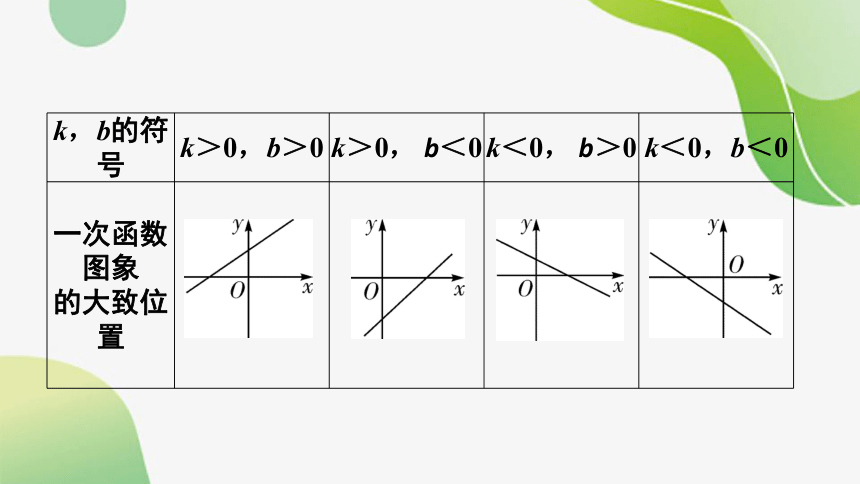



文档简介
(共54张PPT)
数学
人教版
八年级 下册
目 录
CONTENTS
知识网络
01
内容归纳
02
中考完全接触
03
章末整合·感知中考
第
十
九
章
第
十
九
章
1.在某一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量. 2.函数的概念:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
3.画函数图象的一般步骤:①列表;②描点;③连线.
4.描述函数的方法有:①解析式法;②列表法;③图象法.
5.正比例函数的定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
6.一次函数的定义:一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
7.函数的图象:
(1)正比例函数y=kx的图象是经过(0,0)和(1,k)两点的直线.
(2)一次函数y=kx+b的图象是经过(0,b)和(-,0)两点的直线.
8.函数的图象和性质:
函数名称 解析式 性质
正比例函数 y=kx(k≠0) ①k>0,图象在第一、三象限,y随x的增大而增大;
②k<0,图象在第二、四象限,y随x的增大而减小
一次函数 y=kx+b(k≠0) ①k>0,y随x的增大而增大;
②k<0,y随x的增大而减小
k,b的符号 k>0,b>0 k>0, b<0 k<0, b>0 k<0,b<0
一次函数图象 的大致位置
9.待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
待定系数法求一次函数解析式的步骤:
(1)设:先设出一次函数的解析式为y=kx+b(k≠0).
(2)代:将已知条件代入解析式中,建立方程或方程组.
(3)解:解方程或方程组,确定未知系数的值.
(4)写:写出解析式.
10.分段函数的应用,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
11.一元一次方程kx+b=0的解是一次函数y=kx+b的图象与x轴交点(-,0)的横坐标,即x=-.
12.求一元一次不等式ax+b>0或ax+b<0(a,b为常数,a≠0)的解,相当于一次函数y=ax+b的函数值y>0或y<0时,求自变量的取值范围,也相当于这个函数图象在x轴上方或下方时,找对应的x的取值范围.
13.两条直线的交点坐标 两解析式组成的方程组的解.
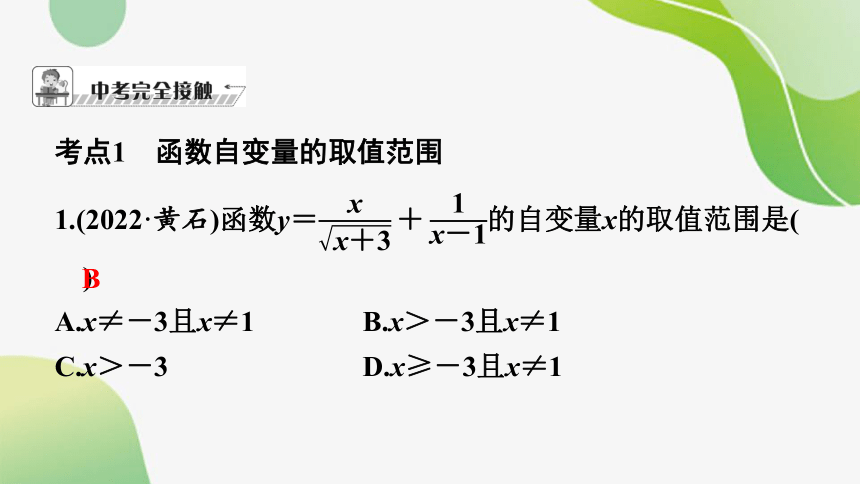
考点1 函数自变量的取值范围
1.(2022·黄石)函数y=的自变量x的取值范围是( )
A.x≠-3且x≠1 B.x>-3且x≠1
C.x>-3 D.x≥-3且x≠1
B
2.(2022·哈尔滨)在函数y=中,自变量x的取值范围是 .
x≠-
考点2 一次函数的图象与性质
3.(2022·株洲)在平面直角坐标系中,一次函数y=5x+1的图象与y轴的交点的坐标为( )
A.(0,-1) B.(-,0) C.(,0) D.(0,1)
D
4.(2022·绍兴)已知(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,且x1<x2<x3,则以下判断正确的是( ).
A.若x1x2>0,则y1y3>0 B.若x1x3<0,则y1y2>0
C.若x2x3>0,则y1y3>0 D.若x2x3<0,则y1y2>0
D
5.(2021·福建)如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式k(x-1)+b>0的解集是( )
A.x>-2
B.x>-1
C.x>0
D.x>1
C
6.(2020·镇江)一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图象不经过的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
7.(2020·济南)若m<-2,则一次函数y=(m+1)x+1-m的图象可能是( )
D
8.(2020·青海)将一个盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示.小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为图中的( )
第8题图
B
9.(2020·铜仁)如图,在矩形ABCD中,AB=3,BC=4.动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y.那么,y与x之间的函数解析式的图象大致是( )
A B C D
D
10.(2020·滨州)如图,在平面直角坐标系中,直线y1=-x-1与直线y2=-2x+2相交于点P,并分别与x轴相交于点A,B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y2=-2x+2在
直线y1=-x-1上方的部分描黑加粗,并写出此时自变量x的取值范围.
解:(1)由题意,得解得
∴点P的坐标为(2,-2).
(2)在直线y1=-x-1与直线y2=-2x+2中,
将y=0代入-x-1=0,得x=-2,
将y=0代入-2x+2=0,得x=1,
∴A(-2,0),B(1,0).
∴AB=3.
∴S△PAB=AB·×3×2=3.
(3)如图所示.
自变量x的取值范围是x<2.
考点3 一次函数的平移
11.(2022·广安)在平面直角坐标系中,将函数y=3x+2的图象向下平移3个单位长度,所得的函数的解析式是( )
A.y=3x+5 B.y=3x-5
C.y=3x+1 D.y=3x-1
D
12.(2020·天津)将直线y=-2x向上平移1个单位长度,平移后直线的解析式为 .
12.y=-2x+1
考点4 一次函数与方程(组)、不等式的关系
13.(2022·南通)根据图象,可得关于x的不等式kx>-x+3的解集是( )
A.x<2
B.x>2
C.x<1
D.x>1
第13题图
D
14.(2022·贵阳)在同一平面直角坐标系中,一次函数y1=ax+b与y2=mx+n(a<m<0)的图象如图所示,小星根据图象得到如下结论:
①在一次函数y=mx+n的图象中,y的值随着x值的增大而增大;
第14题图
②方程组的解为
③方程mx+n=0的解为x=2;
④当x=0时,ax+b=-1.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
B
15.(2022·扬州)如图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为 .
第15题图
x<-1
考点5 一次函数的应用
16.(2022·哈尔滨)一辆汽车油箱中剩余的油量y(L)与已行驶的路程x(km)的对应关系如图所示,如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为35 L时,那么该汽车已行驶的路程为( )
A.150 km B.160 km
C.125 km D.350 km
A
17.(2020·潍坊)若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.函数y=(x+2) (x-1)的图象大致是( )
A
18.(2020·上海)小明从家步行到学校需走的路程为1 800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分)的函数关系.根据图象提供的信息可知,小明从家出发去学校,当步行了15分钟时,到学校还需步行 米.
350
19.(2022·吉林)李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温y(℃)与加热时间x(s)之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
(1)加热前水温是 ℃;
20
解析:由函数图象可知,当x=0时,y=20,
则加热前水温是20 ℃.
(2)求乙壶中水温y关于加热时间x的函数解析式;
解:因为甲壶比乙壶加热速度快,
所以乙壶对应的函数图象经过点(0,20),(160,80),
设乙壶中水温y关于加热时间x的函数解析式为y=kx+b(k≠0),
将点(0,20),(160,80)代入,得
解得
则乙壶中水温y关于加热时间x的函数解析式为y=
x+20,
自变量x的取值范围是0≤x≤160.
(3)当甲壶中水温刚达到80 ℃时,乙壶中水温是 ℃.
65
解析:设甲壶中水温y关于加热时间x的函数解析式为y=mx+n(m≠0),
将点(0,20),(80,60)代入,得
解得
则甲壶中水温y关于加热时间x的函数解析式为y=
x+20,
当y=80时,x+20=80,解得x=120,
将x=120代入y=x+20,得y=×120+20=65,
即当甲壶中水温刚达到80 ℃时,乙壶中水温是65 ℃.
20.(2022·凉山)某班计划采购A,B两种类型的羽毛球拍,已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元;购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.
(1)求A,B两种类型羽毛球拍的单价.
(2)该班准备采购A,B两种类型的羽毛球拍共30副,且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,请给出最省钱的购买方案,求出最少费用,并说明理由.
(1)解:设A型羽毛球拍的单价为x元,B型羽毛球拍的单价为y元,
由题意得:解得
答:A型羽毛球拍的单价为40元,B型羽毛球拍的单价为32元.
(2)解:设该班采购A型羽毛球拍m副,购买的费用为W元,则采购B型羽毛球拍(30-m)副,
由(1)的结论得W=40m+32(30-m)=8m+960,
∵A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,
∴
解得20≤m<30,
在20≤m<30内,W随m的增大而增大,
则当m=20时,W取得最小值,最小值为8×20+960=1 120(元),
此时30-m=30-20=10,
答:最省钱的购买方案是采购20副A型羽毛球拍,10副B型羽毛球拍;最少费用为1 120元.
21.(2020·济南)5G时代的到来,将给人类生活带来巨大改变.现有A,B两种型号的5G手机,进价和售价如表所示:
型号 进价/(元/部) 售价/(元/部)
A 3 000 3 400
B 3 500 4 000
某营业厅购进A,B两种型号的手机共花费32 000元,手机销售完成后共获得利润4 400元.
(1)营业厅购进A,B两种型号的手机各多少部
(2)若营业厅再次购进A,B两种型号的手机共30部,其中B种型号手机的数量不多于A种型号手机数量的2倍.营业厅购进两种型号的手机各多少部时能获得最大利润 最大利润是多少
解:(1)设营业厅购进A种型号的手机a部,购进B种型号的手机b部.
由题意,得
解得
答:营业厅购进A种型号的手机6部,购进B种型号的手机4部.
(2)设营业厅购进A种型号的手机x部,则购进B种型号的手机
(30-x)部,获得的利润为w元.
w=(3 400-3 000)x+(4 000-3 500)(30-x)=-100x+15 000.
∵B种型号手机的数量不多于A种型号手机数量的2倍,
∴30-x≤2x.
解得x≥10.
∵w=-100x+15 000,k=-100,
∴w随x的增大而减小.
∴当x=10时,w取得最大值.
w最大值=-100×10+15 000=14 000(元).
30-x=20.
答:营业厅购进A种型号的手机10部,B种型号的手机20部时能获得最大利润,最大利润是14 000元.
22.(2020·深圳)端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.
(1)肉粽和蜜枣粽的进货单价分别是多少元
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽的数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变.若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,则第二批购进肉粽多少个时,全部售完后,第二批粽子获得的利润最大 第二批粽子的最大利润是多少元
解:(1)设蜜枣粽的进货单价是x元,则肉粽的进货单价是(x+6)元.
由题意,得50(x+6)+30x=620.
解得x=4.
x+6=10.
答:蜜枣粽的进货单价是4元,肉粽的进货单价是10元.
(2)设第二批购进肉粽y个,则购进蜜枣粽(300-y)个,
获得的利润为w元.
由题意,得w=(14-10)y+(6-4)(300-y)=2y+600.
∵肉粽的数量不多于蜜枣数量的2倍,
∴y≤2(300-y),
∴0<y≤200.
∵2>0,
∴w随y的增大而增大.
∴当y=200时,w取得最大值.
此时w最大值=400+600=1 000(元).
答:第二批购进肉粽200个时,获得的利润最大,最大利润是1 000元.
23.(2020·广东)某社区拟建A,B两类摊位,每个A类摊位的占地面积比每个B类摊位的占地面积多2 m2.建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元.用60 m2建A类摊位的个数恰好是用同样面积建B类摊位个数的.
(1)求每个A,B类摊位占地面积各为多少平方米;
(2)该社区拟建A,B两类摊位共90个,且B类摊位的数量不少于A类摊位数量的3倍.求建这90个摊位的最大费用.
解:(1)设每个B类摊位的占地面积为x m2,则每个A类摊位的占地面积为(x+2)m2.
根据题意,得.
解得x=3.
经检验,x=3是原分式方程的解,且符合题意.
x+2=5.
答:每个A类摊位的占地面积为5 m2,每个B类摊位的占地面积为3 m2.
(2)解法一:设建A类摊位a个,建B类摊位(90-a)个,建这90个摊位的费用为y元.
由题意,得y=5a×40+3×30(90-a)=110a+8 100.
∵B类摊位的数量不少于A类摊位数量的3倍,
∴90-a≥3a,∴a≤22.5.
∵110>0,∴y随a的增大而增大,
∵a为整数,
∴当a取最大值22时,w取得最大值.
w最大值=110×22+8 100=10 520(元).
答:建这90个摊位的最大费用为10 520元.
解法二:设建A类摊位a(a为整数)个,建B类摊位(90-a)个.
由题意,得90-a≥3a.
解得a≤22.5.
∵建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,
∴要想使建这90个摊位有最大费用,则要多建造A类摊位,即a取最大值22时,费用最大.
此时最大费用=22×40×5+30×(90-22)×3=10 520(元).
答:建这90个摊位的最大费用为10 520元.
数学
人教版
八年级 下册
目 录
CONTENTS
知识网络
01
内容归纳
02
中考完全接触
03
章末整合·感知中考
第
十
九
章
第
十
九
章
1.在某一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量. 2.函数的概念:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
3.画函数图象的一般步骤:①列表;②描点;③连线.
4.描述函数的方法有:①解析式法;②列表法;③图象法.
5.正比例函数的定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
6.一次函数的定义:一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
7.函数的图象:
(1)正比例函数y=kx的图象是经过(0,0)和(1,k)两点的直线.
(2)一次函数y=kx+b的图象是经过(0,b)和(-,0)两点的直线.
8.函数的图象和性质:
函数名称 解析式 性质
正比例函数 y=kx(k≠0) ①k>0,图象在第一、三象限,y随x的增大而增大;
②k<0,图象在第二、四象限,y随x的增大而减小
一次函数 y=kx+b(k≠0) ①k>0,y随x的增大而增大;
②k<0,y随x的增大而减小
k,b的符号 k>0,b>0 k>0, b<0 k<0, b>0 k<0,b<0
一次函数图象 的大致位置
9.待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
待定系数法求一次函数解析式的步骤:
(1)设:先设出一次函数的解析式为y=kx+b(k≠0).
(2)代:将已知条件代入解析式中,建立方程或方程组.
(3)解:解方程或方程组,确定未知系数的值.
(4)写:写出解析式.
10.分段函数的应用,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
11.一元一次方程kx+b=0的解是一次函数y=kx+b的图象与x轴交点(-,0)的横坐标,即x=-.
12.求一元一次不等式ax+b>0或ax+b<0(a,b为常数,a≠0)的解,相当于一次函数y=ax+b的函数值y>0或y<0时,求自变量的取值范围,也相当于这个函数图象在x轴上方或下方时,找对应的x的取值范围.
13.两条直线的交点坐标 两解析式组成的方程组的解.
考点1 函数自变量的取值范围
1.(2022·黄石)函数y=的自变量x的取值范围是( )
A.x≠-3且x≠1 B.x>-3且x≠1
C.x>-3 D.x≥-3且x≠1
B
2.(2022·哈尔滨)在函数y=中,自变量x的取值范围是 .
x≠-
考点2 一次函数的图象与性质
3.(2022·株洲)在平面直角坐标系中,一次函数y=5x+1的图象与y轴的交点的坐标为( )
A.(0,-1) B.(-,0) C.(,0) D.(0,1)
D
4.(2022·绍兴)已知(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,且x1<x2<x3,则以下判断正确的是( ).
A.若x1x2>0,则y1y3>0 B.若x1x3<0,则y1y2>0
C.若x2x3>0,则y1y3>0 D.若x2x3<0,则y1y2>0
D
5.(2021·福建)如图,一次函数y=kx+b(k>0)的图象过点(-1,0),则不等式k(x-1)+b>0的解集是( )
A.x>-2
B.x>-1
C.x>0
D.x>1
C
6.(2020·镇江)一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,它的图象不经过的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
7.(2020·济南)若m<-2,则一次函数y=(m+1)x+1-m的图象可能是( )
D
8.(2020·青海)将一个盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示.小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为图中的( )
第8题图
B
9.(2020·铜仁)如图,在矩形ABCD中,AB=3,BC=4.动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y.那么,y与x之间的函数解析式的图象大致是( )
A B C D
D
10.(2020·滨州)如图,在平面直角坐标系中,直线y1=-x-1与直线y2=-2x+2相交于点P,并分别与x轴相交于点A,B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y2=-2x+2在
直线y1=-x-1上方的部分描黑加粗,并写出此时自变量x的取值范围.
解:(1)由题意,得解得
∴点P的坐标为(2,-2).
(2)在直线y1=-x-1与直线y2=-2x+2中,
将y=0代入-x-1=0,得x=-2,
将y=0代入-2x+2=0,得x=1,
∴A(-2,0),B(1,0).
∴AB=3.
∴S△PAB=AB·×3×2=3.
(3)如图所示.
自变量x的取值范围是x<2.
考点3 一次函数的平移
11.(2022·广安)在平面直角坐标系中,将函数y=3x+2的图象向下平移3个单位长度,所得的函数的解析式是( )
A.y=3x+5 B.y=3x-5
C.y=3x+1 D.y=3x-1
D
12.(2020·天津)将直线y=-2x向上平移1个单位长度,平移后直线的解析式为 .
12.y=-2x+1
考点4 一次函数与方程(组)、不等式的关系
13.(2022·南通)根据图象,可得关于x的不等式kx>-x+3的解集是( )
A.x<2
B.x>2
C.x<1
D.x>1
第13题图
D
14.(2022·贵阳)在同一平面直角坐标系中,一次函数y1=ax+b与y2=mx+n(a<m<0)的图象如图所示,小星根据图象得到如下结论:
①在一次函数y=mx+n的图象中,y的值随着x值的增大而增大;
第14题图
②方程组的解为
③方程mx+n=0的解为x=2;
④当x=0时,ax+b=-1.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
B
15.(2022·扬州)如图,函数y=kx+b(k<0)的图象经过点P,则关于x的不等式kx+b>3的解集为 .
第15题图
x<-1
考点5 一次函数的应用
16.(2022·哈尔滨)一辆汽车油箱中剩余的油量y(L)与已行驶的路程x(km)的对应关系如图所示,如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为35 L时,那么该汽车已行驶的路程为( )
A.150 km B.160 km
C.125 km D.350 km
A
17.(2020·潍坊)若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.函数y=(x+2) (x-1)的图象大致是( )
A
18.(2020·上海)小明从家步行到学校需走的路程为1 800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分)的函数关系.根据图象提供的信息可知,小明从家出发去学校,当步行了15分钟时,到学校还需步行 米.
350
19.(2022·吉林)李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温y(℃)与加热时间x(s)之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
(1)加热前水温是 ℃;
20
解析:由函数图象可知,当x=0时,y=20,
则加热前水温是20 ℃.
(2)求乙壶中水温y关于加热时间x的函数解析式;
解:因为甲壶比乙壶加热速度快,
所以乙壶对应的函数图象经过点(0,20),(160,80),
设乙壶中水温y关于加热时间x的函数解析式为y=kx+b(k≠0),
将点(0,20),(160,80)代入,得
解得
则乙壶中水温y关于加热时间x的函数解析式为y=
x+20,
自变量x的取值范围是0≤x≤160.
(3)当甲壶中水温刚达到80 ℃时,乙壶中水温是 ℃.
65
解析:设甲壶中水温y关于加热时间x的函数解析式为y=mx+n(m≠0),
将点(0,20),(80,60)代入,得
解得
则甲壶中水温y关于加热时间x的函数解析式为y=
x+20,
当y=80时,x+20=80,解得x=120,
将x=120代入y=x+20,得y=×120+20=65,
即当甲壶中水温刚达到80 ℃时,乙壶中水温是65 ℃.
20.(2022·凉山)某班计划采购A,B两种类型的羽毛球拍,已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元;购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.
(1)求A,B两种类型羽毛球拍的单价.
(2)该班准备采购A,B两种类型的羽毛球拍共30副,且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,请给出最省钱的购买方案,求出最少费用,并说明理由.
(1)解:设A型羽毛球拍的单价为x元,B型羽毛球拍的单价为y元,
由题意得:解得
答:A型羽毛球拍的单价为40元,B型羽毛球拍的单价为32元.
(2)解:设该班采购A型羽毛球拍m副,购买的费用为W元,则采购B型羽毛球拍(30-m)副,
由(1)的结论得W=40m+32(30-m)=8m+960,
∵A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍,
∴
解得20≤m<30,
在20≤m<30内,W随m的增大而增大,
则当m=20时,W取得最小值,最小值为8×20+960=1 120(元),
此时30-m=30-20=10,
答:最省钱的购买方案是采购20副A型羽毛球拍,10副B型羽毛球拍;最少费用为1 120元.
21.(2020·济南)5G时代的到来,将给人类生活带来巨大改变.现有A,B两种型号的5G手机,进价和售价如表所示:
型号 进价/(元/部) 售价/(元/部)
A 3 000 3 400
B 3 500 4 000
某营业厅购进A,B两种型号的手机共花费32 000元,手机销售完成后共获得利润4 400元.
(1)营业厅购进A,B两种型号的手机各多少部
(2)若营业厅再次购进A,B两种型号的手机共30部,其中B种型号手机的数量不多于A种型号手机数量的2倍.营业厅购进两种型号的手机各多少部时能获得最大利润 最大利润是多少
解:(1)设营业厅购进A种型号的手机a部,购进B种型号的手机b部.
由题意,得
解得
答:营业厅购进A种型号的手机6部,购进B种型号的手机4部.
(2)设营业厅购进A种型号的手机x部,则购进B种型号的手机
(30-x)部,获得的利润为w元.
w=(3 400-3 000)x+(4 000-3 500)(30-x)=-100x+15 000.
∵B种型号手机的数量不多于A种型号手机数量的2倍,
∴30-x≤2x.
解得x≥10.
∵w=-100x+15 000,k=-100,
∴w随x的增大而减小.
∴当x=10时,w取得最大值.
w最大值=-100×10+15 000=14 000(元).
30-x=20.
答:营业厅购进A种型号的手机10部,B种型号的手机20部时能获得最大利润,最大利润是14 000元.
22.(2020·深圳)端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.
(1)肉粽和蜜枣粽的进货单价分别是多少元
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽的数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变.若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,则第二批购进肉粽多少个时,全部售完后,第二批粽子获得的利润最大 第二批粽子的最大利润是多少元
解:(1)设蜜枣粽的进货单价是x元,则肉粽的进货单价是(x+6)元.
由题意,得50(x+6)+30x=620.
解得x=4.
x+6=10.
答:蜜枣粽的进货单价是4元,肉粽的进货单价是10元.
(2)设第二批购进肉粽y个,则购进蜜枣粽(300-y)个,
获得的利润为w元.
由题意,得w=(14-10)y+(6-4)(300-y)=2y+600.
∵肉粽的数量不多于蜜枣数量的2倍,
∴y≤2(300-y),
∴0<y≤200.
∵2>0,
∴w随y的增大而增大.
∴当y=200时,w取得最大值.
此时w最大值=400+600=1 000(元).
答:第二批购进肉粽200个时,获得的利润最大,最大利润是1 000元.
23.(2020·广东)某社区拟建A,B两类摊位,每个A类摊位的占地面积比每个B类摊位的占地面积多2 m2.建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元.用60 m2建A类摊位的个数恰好是用同样面积建B类摊位个数的.
(1)求每个A,B类摊位占地面积各为多少平方米;
(2)该社区拟建A,B两类摊位共90个,且B类摊位的数量不少于A类摊位数量的3倍.求建这90个摊位的最大费用.
解:(1)设每个B类摊位的占地面积为x m2,则每个A类摊位的占地面积为(x+2)m2.
根据题意,得.
解得x=3.
经检验,x=3是原分式方程的解,且符合题意.
x+2=5.
答:每个A类摊位的占地面积为5 m2,每个B类摊位的占地面积为3 m2.
(2)解法一:设建A类摊位a个,建B类摊位(90-a)个,建这90个摊位的费用为y元.
由题意,得y=5a×40+3×30(90-a)=110a+8 100.
∵B类摊位的数量不少于A类摊位数量的3倍,
∴90-a≥3a,∴a≤22.5.
∵110>0,∴y随a的增大而增大,
∵a为整数,
∴当a取最大值22时,w取得最大值.
w最大值=110×22+8 100=10 520(元).
答:建这90个摊位的最大费用为10 520元.
解法二:设建A类摊位a(a为整数)个,建B类摊位(90-a)个.
由题意,得90-a≥3a.
解得a≤22.5.
∵建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,
∴要想使建这90个摊位有最大费用,则要多建造A类摊位,即a取最大值22时,费用最大.
此时最大费用=22×40×5+30×(90-22)×3=10 520(元).
答:建这90个摊位的最大费用为10 520元.
