2023-2024学年数学八年级下册期中测试试题(冀教版)基础卷含解析
文档属性
| 名称 | 2023-2024学年数学八年级下册期中测试试题(冀教版)基础卷含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学八年级下册(冀教版)
期中测试 基础卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共36分)
1.(本题3分)为了解某校480名八年级学生的睡眠时间,从中抽取80名学生进行调查,下列说法正确的是( )
A.480名学生是总体 B.样本容量是80名
C.每名学生是个体 D.80名学生的睡眠时间是总体的一个样本
2.(本题3分)如图是某天参观周恩来纪念馆的学生人数统计图.若大学生有600人,则初中生有( )
A.1000人 B.1200人 C.1800人 D.1500人
3.(本题3分)小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:则通话时间不超过的频率是( )
通话时间
频数(通话次数) 20 16 9 5
A. B. C. D.
4.(本题3分)为保护人类赖以生存的生态环境,我国将每年的3月12日定为中国植树节.在植树节当天,某校组织各班级进行植树活动,事后统计了各班级种植树木的数量,绘制成如下频数分布直方图(每组含前一个数值,不含后一个数值):
根据统计结果,下列说法错误的是( )
A.共有24个班级参加植树活动 B.频数分布直方图的组距为5
C.有的班级种植树木的数量少于35棵 D.有3个班级都种了45棵树
5.(本题3分)如果,那么点在( )
A.第二象限 B.第四象限
C.第四象限或第二象限 D.第一象限或第三象限
6.(本题3分)将线段平移得到线段,点的对应点为,的对应点D的坐标为( )
A. B. C. D.
7.(本题3分)如图,在的点阵中,甲、乙、丙、丁四个玻璃球分别从四个点处同时出发,按各自箭头方向作匀速直线运动,运动秒后分别到达、、、处,若按照上述方式继续运动,则第一次发生碰撞的是( )
A.甲和乙 B.甲和丙 C.甲和丁 D.丙和丁
8.(本题3分)如图,将边长为的正方形沿轴正方向连续翻转次,点依次落在点、、、、、的位置上,则点的坐标为( )
A. B. C. D.
9.(本题3分)已知:如图,甲、乙两个工程队合作修一条长为3000米的公路,假设甲、乙两个工程队的工作效率是一定的.甲队单独做了20天后,乙队加入合作完成剩下的全部工程.完成的工程量y(米)与工程时间x(天)的关系如图所示.下列结论中错误的是( )
A.完成该工程一共用了30天 B.乙工程队在该工程中一共工作了10天
C.甲工程队每天修路50米 D.乙工程队每天修路200米
10.(本题3分)如图1,在中,,于点.动点从点出发,沿折线方向运动,运动到点停止.设点的运动路程为,的面积为,与的函数图象如图2,则的长为( )
A.6 B.8 C.10 D.13
11.(本题3分)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如表):下列说法错误的是( )
温度/℃
声速/(m/s)
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为℃时,声音可以传播
D.当温度每升高℃,声速增加
12.(本题3分)一个圆形花坛,周长C与半径r的函数关系式为,其中关于常量和变量的表述正确的是( )
A.常量是2,变量是C,π,r B.常量是2,变量是r,π
C.常量是2,变量是C,π D.常量是,变量是C,r
评卷人得分
二、填空题(共18分)
13.(本题3分)已知数据:,,其中有理数出现的频率是 .
14.(本题3分)我市今年共有13800名考生参加中考,为了解这13800名考生的数学成绩,从中抽取了800名考生的数学成绩进行统计分析.在这次调查中,被抽取的800名考生的数学成绩是 (填“总体”“样本”或“个体”).
15.(本题3分)点在第二象限,它到轴、轴的距离分别是、2,则它的坐标是 .
16.(本题3分)点在第四象限,则x的取值范围是 .
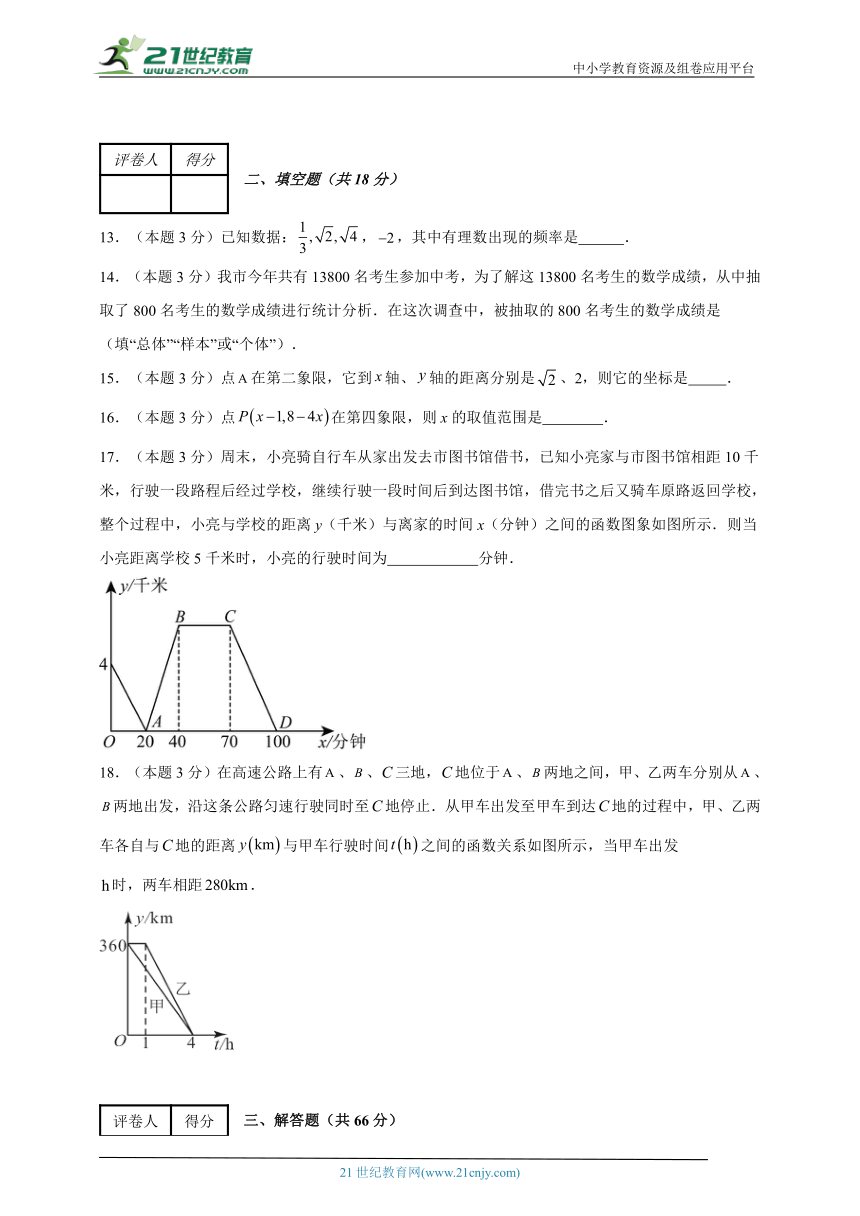
17.(本题3分)周末,小亮骑自行车从家出发去市图书馆借书,已知小亮家与市图书馆相距10千米,行驶一段路程后经过学校,继续行驶一段时间后到达图书馆,借完书之后又骑车原路返回学校,整个过程中,小亮与学校的距离y(千米)与离家的时间x(分钟)之间的函数图象如图所示.则当小亮距离学校5千米时,小亮的行驶时间为 分钟.
18.(本题3分)在高速公路上有、、三地,地位于、两地之间,甲、乙两车分别从、两地出发,沿这条公路匀速行驶同时至地停止.从甲车出发至甲车到达地的过程中,甲、乙两车各自与地的距离与甲车行驶时间之间的函数关系如图所示,当甲车出发 时,两车相距.
评卷人得分
三、解答题(共66分)
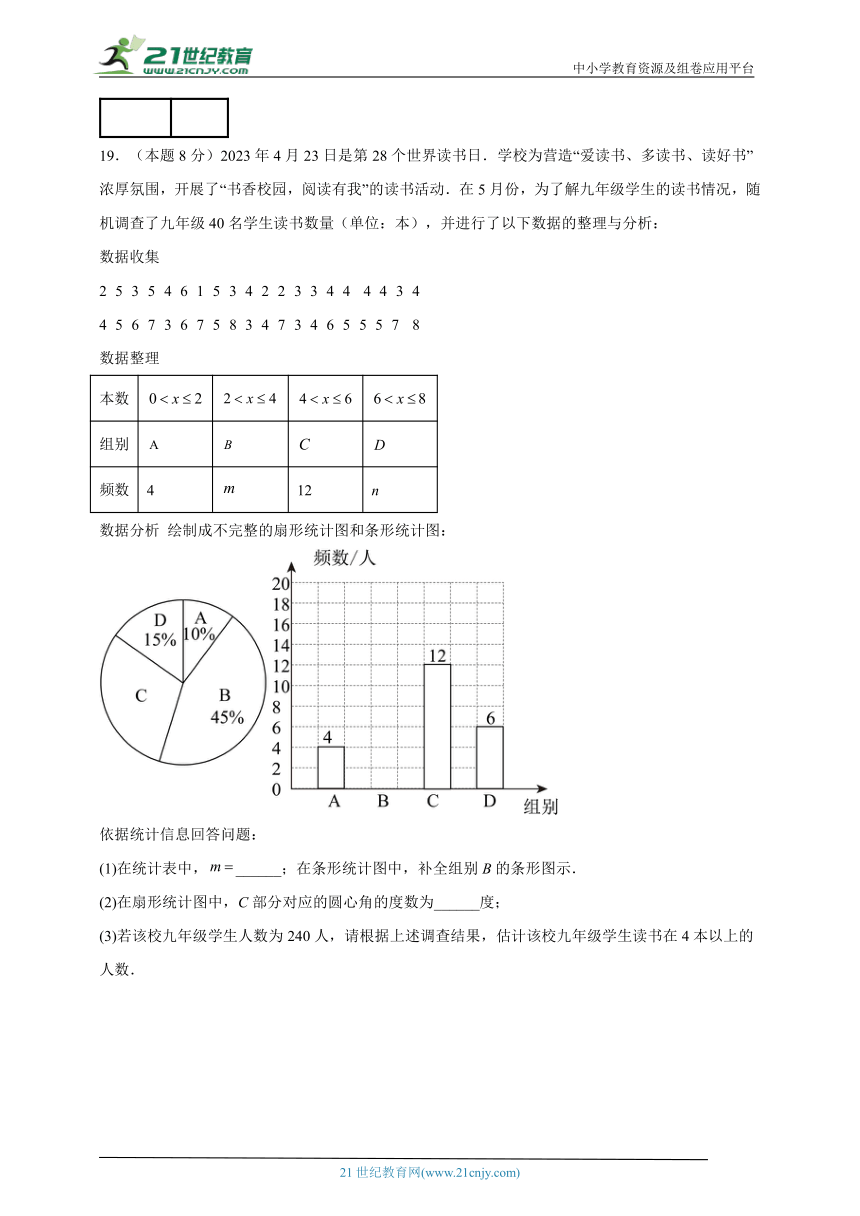
19.(本题8分)2023年4月23日是第28个世界读书日.学校为营造“爱读书、多读书、读好书”浓厚氛围,开展了“书香校园,阅读有我”的读书活动.在5月份,为了解九年级学生的读书情况,随机调查了九年级40名学生读书数量(单位:本),并进行了以下数据的整理与分析:
数据收集
2 5 3 5 4 6 1 5 3 4 2 2 3 3 4 4 4 4 3 4
4 5 6 7 3 6 7 5 8 3 4 7 3 4 6 5 5 5 7 8
数据整理
本数
组别
频数 4 12 n
数据分析 绘制成不完整的扇形统计图和条形统计图:
依据统计信息回答问题:
(1)在统计表中,______;在条形统计图中,补全组别B的条形图示.
(2)在扇形统计图中,C部分对应的圆心角的度数为______度;
(3)若该校九年级学生人数为240人,请根据上述调查结果,估计该校九年级学生读书在4本以上的人数.
20.(本题8分)某学校为了解全校学生利用课外时间进行体育锻炼的情况,学校团委随机抽取若干名学生,调查他们一周的课外锻炼时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
锻炼时间(小时) 频数(人) 频率
18
a
45
36 n
21
合计 b 1
(1)填空: , , ;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校有3000名学生,请根据上述调查结果,估算该校学生一周的课外锻炼时间不足三小时的人数.
21.(本题10分)如图,在边长为1的正方形组成的网格中,的顶点均在格点上,以点O为原点建立平面直角坐标系.
(1)与关于点O成中心对称,请画出;
(2)将绕点O逆时针旋转后得到,请在图中画出;
(3)的面积是_______.
22.(本题10分)已知关于,的方程组,为常数.
(1)求方程组的解(用含的式子表示);
(2)平面直角坐标系中,若以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,求的值.
23.(本题10分)“龟兔赛跑”是一则著名的寓言故事,请完成下列问题:
(1)图①描绘的场景对应图③中的点______,图②描绘的场景对应图③中的点______;
(2)你认为图③中的线段与线段是否平行?请说明你的理由;
(3)如果龟兔约定按照相同的规则再比赛一次,且兔龟都没睡觉兔子先到达终点,请在图④画出比赛的大致函数图像.
24.(本题10分)甲、乙两人匀速从同一地点A沿相同线路到1200米的B处,甲出发4分钟时乙骑单车以每分钟150米的速度行走,设甲、乙两人相距s(米)(分钟),s关于t的函数图象的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中补全s关于t的图象;
(3)当甲、乙两人相距240米时,求甲到B地的距离.
25.(本题10分)如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)将向上平移4格,画出平移后的;
(2)将以点O为旋转中心顺时针旋转,画出旋转后对应的;
(3)若绕点M旋转能得到,则旋转中心点M的坐标为 ___________.
参考答案:
1.D
【分析】本题主要考查了总体、个体、样本、样本容量的定义,根据总体、个体、样本、样本容量的知识解答.总体是指所要考查对象的全体;个体是指每一个考查对象;样本是指从总体中抽取的部分考查对象称为样本;样本容量是指样本所含个体的个数(不含单位).
【详解】解:A、480名学生的睡眠时间是总体,原说法错误,不符合题意;
B、样本容量是80,原说法错误,不符合题意;
C、每名学生的睡眠时间是个体,原说法错误,不符合题意;
D、80名学生的睡眠时间是总体的一个样本,原说法正确,符合题意;
故选;D.
2.B
【分析】本题考查扇形统计图.根据题意可知,样本中大学生有600人,占调查人数的,由频率即可求出调查人数,进而样本中的初中生人数即可.
【详解】解:调查人数为:(人,
样本中初中生人数:(人,
故选:B.
3.D
【分析】本题考查了频数分布表的知识,解题的关键是了解频率频数样本容量,难度不大.
不超过的通话时间除以所有的通话时间即可求得通话时间不超过的频率.
【详解】解:不超过的通话次数为(次,
通话总次数为(次,
通话时间不超过的频率为:;
故选:D.
4.D
【分析】本题考查直方图,从直方图中获取信息,逐一进行判断即可.
【详解】解:A、共有个班级参加植树活动,正确;
B、频数分布直方图的组距为5,正确;
C、有的班级种植树木的数量少于35棵,正确;
D、有3个班级都种了棵树,选项错误;
故选D.
5.C
【分析】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,解题的关键是掌握四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
根据平面直角坐标系中各个象限的点的坐标特点解答即可.
【详解】解:∵,
∴与异号,
∴点在第四象限或第二象限,
故选:C.
6.C
【分析】本题考查了根据对应两点的坐标确定平移,求平移后点的坐标,关键是确定平移规律.先确定平移规律:向右平移5个单位,向上平移3个单位,再根据平移规律即可确定点D的坐标.
【详解】解:∵点的对应点C的坐标为,
∴平移规律为向右平移5个单位,向上平移3个单位,
∴的对应点D的坐标为,即.
故选:C.
7.B
【分析】本题考查了图形的变化类,先画各个球的运动路径,再根据图示即可求解,找到变化规律是解题的关键.
【详解】解:各个球继续运动如图示,
由图示得,甲和乙不相撞,甲和丙经过秒相撞,甲和丁不相撞,丙和丁不相撞,
故选:.
8.A
【分析】此题主要考查了通过图形观察规律,根据题意分别求出、、、横坐标,再总结出规律即可得出,解题的关键是善于观察,总结规律.
【详解】根据规律
、、、、
、、、、
,;
每个一个循环, ,
依次规律在次循环后与纵坐标一致,
横坐标分别为:为、为、为、为;
为、为、为、为;
依次规律与横坐标为减,
∴横坐标为,
则坐标是,
故选:.
9.D
【分析】本题考查了函数图象获取信息以及一元一次方程的工程问题,正确掌握相关性质内容是解题的关键.根据甲队单独做了20天,完成1000米,得出甲工程队每天修路50米,因为甲、乙两个工程队的工作效率是一定的,则列式,得出乙工程队每天修路150米,结合图象性质,即可作答.
【详解】解:从图象可知,工程时间,所对应的是
∴完成该工程一共用了30天,故A是正确的;
∵(天)
∴乙工程队在该工程中一共工作了10天,故B是正确的;
∵甲队单独做了20天,完成1000米,
∴
即甲工程队每天修路50米;故C是正确的;
设乙工程队每天修路x米,
则
解得
∴乙工程队每天修路150米,故D是错误的
故选:D
10.A
【分析】此题主要考查了等腰三角形的性质,三角形的面积公式,判断出和点和点重合时,的面积为3是解本题的关键.先根据结合图2得出,进而利用勾股定理得,,再由运动结合的面积的变化,得出点和点重合时,的面积最大,其值为3,即,进而建立方程组求解,即可得出结论.
【详解】解:由图2知,,
,
,
,,
,,
在中,①,
设点到的距离为,
,
动点从点出发,沿折线方向运动,
当点运动到点时,的面积最大,即,
由图2知,的面积最大为3,
,
②,
①②得,,
,
(负值舍去),
③,
将③代入②得,,
或,
,
,
,
故选:A.
11.C
【分析】本题考查函数的定义,解题的关键的掌握函数的定义,掌握自变量和因变量的关系,从表格中读取信息,进行判断,即可.
【详解】由函数的定义可得,在这个变化中,自变量是温度,因变量是声速,
∴选项A正确,不符合题意;
∵由表格信息可得,温度越高,声速越快,
∴选项B正确,不符合题意;
∵当空气温度为℃时,声音可以传播距离为,
∴选项C错误,符合题意;
∵由题意得当温度每升高℃,声速增加,
∴选项D正确,不符合题意;
故选:C.
12.D
【分析】本题主要考查了常量和变量,解题的关键是熟练掌握常量和变量的定义,根据定义进行判断即可.
【详解】解:根据题意得:函数关系式中常量是,变量是C、r.
故选:D.
13./
【分析】本题考查了实数的分类和频率的计算.频率的计算方法:频率=频数÷总数.
本题中实数有4个,有理数有,,这三个,代入频率计算公式即可.
【详解】解:在4个数中,有理数有,,,所以有理数出现的频率为,
故答案为:.
14.样本
【分析】本题主要考查了总体、个体、样本、样本容量的定义,总体是指所要考查对象的全体;个体是指每一个考查对象;样本是指从总体中抽取的部分考查对象称为样本;样本容量是指样本所含个体的个数(不含单位),据此求解即可.
【详解】解:由题意得,被抽取的800名考生的数学成绩是样本,
故答案为:样本.
15.
【分析】本题考查了点的坐标特征,设点的坐标为,根据点在第二象限,它到轴、轴的距离分别是、2,得出,,即可得出答案.
【详解】解:设点的坐标为,
∵点在第二象限,它到轴、轴的距离分别是、2,
∴,,
∵点在第二象限,
∴,,
,,
∴坐标为.
故答案为:.
16.
【分析】本题考查根据点所在的象限,求参数.根据第四象限的点的符号特征,得到进行求解即可.
【详解】解:∵点在第四象限,
∴
解得:.
故答案为:.
17.或73
【分析】本题主要考查了从函数图象获取信息,由函数图象可知,小明家与学校的距离为4千米,则学校与图书馆的距离为千米,然后分在从学校去图书馆的过程中,小亮距离学校5千米时,在从图书馆回家的过程中,当小亮距离学校5千米时,两种情况根据函数图象求出对应的速度,再根据时间路程速度列式计算求解即可得到答案.
【详解】解:由函数图象可知,小明家与学校的距离为4千米,则学校与图书馆的距离为千米,
在从学校去图书馆的过程中,小亮的速度为千米/分钟,
∴在从学校去图书馆的过程中,当小亮距离学校5千米时,小亮的行驶时间为分钟
在从图书馆回家的过程中,小亮的速度为千米/分钟,
∴在从图书馆回家的过程中,当小亮距离学校5千米时,小亮的行驶时间为分钟;
综上所述,当小亮距离学校5千米时,小亮的行驶时间为分钟或73分钟,
故答案为:或73.
18./
【分析】本题主要考查一次函数的应用,利用题意找出等量关系是解题关键.根据题意结合图象,可得与的距离等于与的距离均为,根据行驶路程与时间的关系,可得两车的速度,设甲出发小时后,两车相距,由题意,得,解出即可完成解答..
【详解】解:由题意并结合图形可得:,
甲的速度:,
乙的速度:,
设甲出发小时后,两车相距,
由题意得:,
解得:,
故答案为:.
19.(1)18,图形见解析;
(2)108;
(3)读书在4本以上的人数大约有108人.
【分析】本题考查扇形统计图,样本估计总体的思想,频数分布等知识,解题的关键是熟练掌握基本知识,理解样本和总体的关系.
(1)由随机调查的九年级40名学生读书数量的数据直接得出m的值;
(2)根据读书数量在C组对应人数求出百分比再乘以360 即可得到对应的圆心角;
(3)利用样本估计总体的思想解决问题即可.
【详解】(1)由条形统计图可得:
(2)解:,,
故答案为:.
(3)解:∵40人中共有名学生读书在4本以上,
∴(人)
答:该校八年级学生读书在4本以上的人数为108人.
20.(1)30,150,
(2)见解析
(3)该校学生一周的课外锻炼时间不足三小时的人数为960人
【分析】
本题考查的是频数(率)分布表与条形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
(1)根据阅读时间为的人数及所占百分比可得,求出总人数,再根据频率、频数、总人数的关系即可求出a、b、n;
(2)根据数据将频数分布直方图补充完整即可;
(3)由总人数乘以时间不足三小时的人数的频率即可.
【详解】(1)解:(人),
,
,
故答案为:30,150,0.24
(2)解:如图所示:
(3)解:(人)
即估算该校学生一周的课外锻炼时间不足三小时的人数为960人.
21.(1)见解析
(2)见解析
(3)
【分析】本题主要考查了坐标与图形变化—中心对称,旋转,割补法求三角形面积:
(1)根据关于原点对称的点横纵坐标都互为相反数得到A、B对应点的位置,然后顺次连接
(2)根据所给旋转方式结合网格的特点得到A、B对应点的位置,然后顺次连接即可;
(3)用所在的长方形面积进去周围三个三角形的面积即可得到答案.
【详解】(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:.
故答案为:.
22.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,一,三象限角平分线上点的坐标特点,熟练的解方程组是解本题的关键.
(1)直接利用加减消元法解方程组即可;
(2)由一,三象限角平分线上的点的横纵坐标相等,再建立方程求解即可.
【详解】(1)解:,
,得,
∴.
将代入①,得.
原方程组的解为:;
(2)∵以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,
∴,
解得:.
23.(1)B,D
(2)不平行,理由见详解
(3)图见详解
【分析】本题主要考查函数图像,解题的关键是理解题意;
(1)根据图像及题意可进行求解;
(2)根据图像可进行求解;
(3)根据题意可直接画出函数图像
【详解】(1)解:图①描绘的场景对应图③中的点B,图②描绘的场景对应图③中的点D;
故答案为B,D;
(2)解:线段与线段不平行;理由是因为兔子在发现自己被乌龟赶超了,速度肯定会有所提升,这样就比刚开始比赛时的速度更快,结合速度、时间和路程是成正比例关系的,速度越快,代表着直线的倾斜度也越陡,所以这两条直线是不会平行的;
(3)解:由题意可得如下图像:
24.(1)甲的速度为
(2)图见解析
(3)甲到地的距离为或.
【分析】本题考查从函数图象获取信息,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)根据图象中的数据可知:甲走了,然后即可计算出甲的速度;
(2)根据图象和(1)中的结果,可以计算出甲到达地用的总的时间,然后即可将图象补充完整;
(3)根据题意可知,存在两种情况,然后计算出即可.
【详解】(1)由图象可得,
甲的速度为:,
即甲的速度为;
(2),
甲到达地用的总的时间为:,
补全的图象如右图所示;
(3)设甲走时,甲、乙两人相距240米,
乙到达地前:,
解得,
则此时甲离地的距离为:;
当乙到达地后,当甲、乙两人相距240米时,此时甲到地的距离就是;
答:当甲、乙两人相距240米时,甲到地的距离为或.
25.(1)见解析
(2)见解析
(3)
【分析】本题考查作图﹣旋转变换、平移变换,熟练掌握旋转的性质、平移的性质是解答本题的关键.
(1)根据平移的性质作图即可.
(2)根据旋转的性质作图即可.
(3)连接,,,相交于点M,则绕点M旋转能得到,即可得出答案.
【详解】(1)如图,即为所求.
(2)如图,即为所求.
(3)连接,,,相交于点M,
则则绕点M旋转能得到
由图可得,旋转中心点M的坐标为.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学八年级下册(冀教版)
期中测试 基础卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共36分)
1.(本题3分)为了解某校480名八年级学生的睡眠时间,从中抽取80名学生进行调查,下列说法正确的是( )
A.480名学生是总体 B.样本容量是80名
C.每名学生是个体 D.80名学生的睡眠时间是总体的一个样本
2.(本题3分)如图是某天参观周恩来纪念馆的学生人数统计图.若大学生有600人,则初中生有( )
A.1000人 B.1200人 C.1800人 D.1500人
3.(本题3分)小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:则通话时间不超过的频率是( )
通话时间
频数(通话次数) 20 16 9 5
A. B. C. D.
4.(本题3分)为保护人类赖以生存的生态环境,我国将每年的3月12日定为中国植树节.在植树节当天,某校组织各班级进行植树活动,事后统计了各班级种植树木的数量,绘制成如下频数分布直方图(每组含前一个数值,不含后一个数值):
根据统计结果,下列说法错误的是( )
A.共有24个班级参加植树活动 B.频数分布直方图的组距为5
C.有的班级种植树木的数量少于35棵 D.有3个班级都种了45棵树
5.(本题3分)如果,那么点在( )
A.第二象限 B.第四象限
C.第四象限或第二象限 D.第一象限或第三象限
6.(本题3分)将线段平移得到线段,点的对应点为,的对应点D的坐标为( )
A. B. C. D.
7.(本题3分)如图,在的点阵中,甲、乙、丙、丁四个玻璃球分别从四个点处同时出发,按各自箭头方向作匀速直线运动,运动秒后分别到达、、、处,若按照上述方式继续运动,则第一次发生碰撞的是( )
A.甲和乙 B.甲和丙 C.甲和丁 D.丙和丁
8.(本题3分)如图,将边长为的正方形沿轴正方向连续翻转次,点依次落在点、、、、、的位置上,则点的坐标为( )
A. B. C. D.
9.(本题3分)已知:如图,甲、乙两个工程队合作修一条长为3000米的公路,假设甲、乙两个工程队的工作效率是一定的.甲队单独做了20天后,乙队加入合作完成剩下的全部工程.完成的工程量y(米)与工程时间x(天)的关系如图所示.下列结论中错误的是( )
A.完成该工程一共用了30天 B.乙工程队在该工程中一共工作了10天
C.甲工程队每天修路50米 D.乙工程队每天修路200米
10.(本题3分)如图1,在中,,于点.动点从点出发,沿折线方向运动,运动到点停止.设点的运动路程为,的面积为,与的函数图象如图2,则的长为( )
A.6 B.8 C.10 D.13
11.(本题3分)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如表):下列说法错误的是( )
温度/℃
声速/(m/s)
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为℃时,声音可以传播
D.当温度每升高℃,声速增加
12.(本题3分)一个圆形花坛,周长C与半径r的函数关系式为,其中关于常量和变量的表述正确的是( )
A.常量是2,变量是C,π,r B.常量是2,变量是r,π
C.常量是2,变量是C,π D.常量是,变量是C,r
评卷人得分
二、填空题(共18分)
13.(本题3分)已知数据:,,其中有理数出现的频率是 .
14.(本题3分)我市今年共有13800名考生参加中考,为了解这13800名考生的数学成绩,从中抽取了800名考生的数学成绩进行统计分析.在这次调查中,被抽取的800名考生的数学成绩是 (填“总体”“样本”或“个体”).
15.(本题3分)点在第二象限,它到轴、轴的距离分别是、2,则它的坐标是 .
16.(本题3分)点在第四象限,则x的取值范围是 .
17.(本题3分)周末,小亮骑自行车从家出发去市图书馆借书,已知小亮家与市图书馆相距10千米,行驶一段路程后经过学校,继续行驶一段时间后到达图书馆,借完书之后又骑车原路返回学校,整个过程中,小亮与学校的距离y(千米)与离家的时间x(分钟)之间的函数图象如图所示.则当小亮距离学校5千米时,小亮的行驶时间为 分钟.
18.(本题3分)在高速公路上有、、三地,地位于、两地之间,甲、乙两车分别从、两地出发,沿这条公路匀速行驶同时至地停止.从甲车出发至甲车到达地的过程中,甲、乙两车各自与地的距离与甲车行驶时间之间的函数关系如图所示,当甲车出发 时,两车相距.
评卷人得分
三、解答题(共66分)
19.(本题8分)2023年4月23日是第28个世界读书日.学校为营造“爱读书、多读书、读好书”浓厚氛围,开展了“书香校园,阅读有我”的读书活动.在5月份,为了解九年级学生的读书情况,随机调查了九年级40名学生读书数量(单位:本),并进行了以下数据的整理与分析:
数据收集
2 5 3 5 4 6 1 5 3 4 2 2 3 3 4 4 4 4 3 4
4 5 6 7 3 6 7 5 8 3 4 7 3 4 6 5 5 5 7 8
数据整理
本数
组别
频数 4 12 n
数据分析 绘制成不完整的扇形统计图和条形统计图:
依据统计信息回答问题:
(1)在统计表中,______;在条形统计图中,补全组别B的条形图示.
(2)在扇形统计图中,C部分对应的圆心角的度数为______度;
(3)若该校九年级学生人数为240人,请根据上述调查结果,估计该校九年级学生读书在4本以上的人数.
20.(本题8分)某学校为了解全校学生利用课外时间进行体育锻炼的情况,学校团委随机抽取若干名学生,调查他们一周的课外锻炼时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
锻炼时间(小时) 频数(人) 频率
18
a
45
36 n
21
合计 b 1
(1)填空: , , ;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校有3000名学生,请根据上述调查结果,估算该校学生一周的课外锻炼时间不足三小时的人数.
21.(本题10分)如图,在边长为1的正方形组成的网格中,的顶点均在格点上,以点O为原点建立平面直角坐标系.
(1)与关于点O成中心对称,请画出;
(2)将绕点O逆时针旋转后得到,请在图中画出;
(3)的面积是_______.
22.(本题10分)已知关于,的方程组,为常数.
(1)求方程组的解(用含的式子表示);
(2)平面直角坐标系中,若以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,求的值.
23.(本题10分)“龟兔赛跑”是一则著名的寓言故事,请完成下列问题:
(1)图①描绘的场景对应图③中的点______,图②描绘的场景对应图③中的点______;
(2)你认为图③中的线段与线段是否平行?请说明你的理由;
(3)如果龟兔约定按照相同的规则再比赛一次,且兔龟都没睡觉兔子先到达终点,请在图④画出比赛的大致函数图像.
24.(本题10分)甲、乙两人匀速从同一地点A沿相同线路到1200米的B处,甲出发4分钟时乙骑单车以每分钟150米的速度行走,设甲、乙两人相距s(米)(分钟),s关于t的函数图象的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中补全s关于t的图象;
(3)当甲、乙两人相距240米时,求甲到B地的距离.
25.(本题10分)如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)将向上平移4格,画出平移后的;
(2)将以点O为旋转中心顺时针旋转,画出旋转后对应的;
(3)若绕点M旋转能得到,则旋转中心点M的坐标为 ___________.
参考答案:
1.D
【分析】本题主要考查了总体、个体、样本、样本容量的定义,根据总体、个体、样本、样本容量的知识解答.总体是指所要考查对象的全体;个体是指每一个考查对象;样本是指从总体中抽取的部分考查对象称为样本;样本容量是指样本所含个体的个数(不含单位).
【详解】解:A、480名学生的睡眠时间是总体,原说法错误,不符合题意;
B、样本容量是80,原说法错误,不符合题意;
C、每名学生的睡眠时间是个体,原说法错误,不符合题意;
D、80名学生的睡眠时间是总体的一个样本,原说法正确,符合题意;
故选;D.
2.B
【分析】本题考查扇形统计图.根据题意可知,样本中大学生有600人,占调查人数的,由频率即可求出调查人数,进而样本中的初中生人数即可.
【详解】解:调查人数为:(人,
样本中初中生人数:(人,
故选:B.
3.D
【分析】本题考查了频数分布表的知识,解题的关键是了解频率频数样本容量,难度不大.
不超过的通话时间除以所有的通话时间即可求得通话时间不超过的频率.
【详解】解:不超过的通话次数为(次,
通话总次数为(次,
通话时间不超过的频率为:;
故选:D.
4.D
【分析】本题考查直方图,从直方图中获取信息,逐一进行判断即可.
【详解】解:A、共有个班级参加植树活动,正确;
B、频数分布直方图的组距为5,正确;
C、有的班级种植树木的数量少于35棵,正确;
D、有3个班级都种了棵树,选项错误;
故选D.
5.C
【分析】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,解题的关键是掌握四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
根据平面直角坐标系中各个象限的点的坐标特点解答即可.
【详解】解:∵,
∴与异号,
∴点在第四象限或第二象限,
故选:C.
6.C
【分析】本题考查了根据对应两点的坐标确定平移,求平移后点的坐标,关键是确定平移规律.先确定平移规律:向右平移5个单位,向上平移3个单位,再根据平移规律即可确定点D的坐标.
【详解】解:∵点的对应点C的坐标为,
∴平移规律为向右平移5个单位,向上平移3个单位,
∴的对应点D的坐标为,即.
故选:C.
7.B
【分析】本题考查了图形的变化类,先画各个球的运动路径,再根据图示即可求解,找到变化规律是解题的关键.
【详解】解:各个球继续运动如图示,
由图示得,甲和乙不相撞,甲和丙经过秒相撞,甲和丁不相撞,丙和丁不相撞,
故选:.
8.A
【分析】此题主要考查了通过图形观察规律,根据题意分别求出、、、横坐标,再总结出规律即可得出,解题的关键是善于观察,总结规律.
【详解】根据规律
、、、、
、、、、
,;
每个一个循环, ,
依次规律在次循环后与纵坐标一致,
横坐标分别为:为、为、为、为;
为、为、为、为;
依次规律与横坐标为减,
∴横坐标为,
则坐标是,
故选:.
9.D
【分析】本题考查了函数图象获取信息以及一元一次方程的工程问题,正确掌握相关性质内容是解题的关键.根据甲队单独做了20天,完成1000米,得出甲工程队每天修路50米,因为甲、乙两个工程队的工作效率是一定的,则列式,得出乙工程队每天修路150米,结合图象性质,即可作答.
【详解】解:从图象可知,工程时间,所对应的是
∴完成该工程一共用了30天,故A是正确的;
∵(天)
∴乙工程队在该工程中一共工作了10天,故B是正确的;
∵甲队单独做了20天,完成1000米,
∴
即甲工程队每天修路50米;故C是正确的;
设乙工程队每天修路x米,
则
解得
∴乙工程队每天修路150米,故D是错误的
故选:D
10.A
【分析】此题主要考查了等腰三角形的性质,三角形的面积公式,判断出和点和点重合时,的面积为3是解本题的关键.先根据结合图2得出,进而利用勾股定理得,,再由运动结合的面积的变化,得出点和点重合时,的面积最大,其值为3,即,进而建立方程组求解,即可得出结论.
【详解】解:由图2知,,
,
,
,,
,,
在中,①,
设点到的距离为,
,
动点从点出发,沿折线方向运动,
当点运动到点时,的面积最大,即,
由图2知,的面积最大为3,
,
②,
①②得,,
,
(负值舍去),
③,
将③代入②得,,
或,
,
,
,
故选:A.
11.C
【分析】本题考查函数的定义,解题的关键的掌握函数的定义,掌握自变量和因变量的关系,从表格中读取信息,进行判断,即可.
【详解】由函数的定义可得,在这个变化中,自变量是温度,因变量是声速,
∴选项A正确,不符合题意;
∵由表格信息可得,温度越高,声速越快,
∴选项B正确,不符合题意;
∵当空气温度为℃时,声音可以传播距离为,
∴选项C错误,符合题意;
∵由题意得当温度每升高℃,声速增加,
∴选项D正确,不符合题意;
故选:C.
12.D
【分析】本题主要考查了常量和变量,解题的关键是熟练掌握常量和变量的定义,根据定义进行判断即可.
【详解】解:根据题意得:函数关系式中常量是,变量是C、r.
故选:D.
13./
【分析】本题考查了实数的分类和频率的计算.频率的计算方法:频率=频数÷总数.
本题中实数有4个,有理数有,,这三个,代入频率计算公式即可.
【详解】解:在4个数中,有理数有,,,所以有理数出现的频率为,
故答案为:.
14.样本
【分析】本题主要考查了总体、个体、样本、样本容量的定义,总体是指所要考查对象的全体;个体是指每一个考查对象;样本是指从总体中抽取的部分考查对象称为样本;样本容量是指样本所含个体的个数(不含单位),据此求解即可.
【详解】解:由题意得,被抽取的800名考生的数学成绩是样本,
故答案为:样本.
15.
【分析】本题考查了点的坐标特征,设点的坐标为,根据点在第二象限,它到轴、轴的距离分别是、2,得出,,即可得出答案.
【详解】解:设点的坐标为,
∵点在第二象限,它到轴、轴的距离分别是、2,
∴,,
∵点在第二象限,
∴,,
,,
∴坐标为.
故答案为:.
16.
【分析】本题考查根据点所在的象限,求参数.根据第四象限的点的符号特征,得到进行求解即可.
【详解】解:∵点在第四象限,
∴
解得:.
故答案为:.
17.或73
【分析】本题主要考查了从函数图象获取信息,由函数图象可知,小明家与学校的距离为4千米,则学校与图书馆的距离为千米,然后分在从学校去图书馆的过程中,小亮距离学校5千米时,在从图书馆回家的过程中,当小亮距离学校5千米时,两种情况根据函数图象求出对应的速度,再根据时间路程速度列式计算求解即可得到答案.
【详解】解:由函数图象可知,小明家与学校的距离为4千米,则学校与图书馆的距离为千米,
在从学校去图书馆的过程中,小亮的速度为千米/分钟,
∴在从学校去图书馆的过程中,当小亮距离学校5千米时,小亮的行驶时间为分钟
在从图书馆回家的过程中,小亮的速度为千米/分钟,
∴在从图书馆回家的过程中,当小亮距离学校5千米时,小亮的行驶时间为分钟;
综上所述,当小亮距离学校5千米时,小亮的行驶时间为分钟或73分钟,
故答案为:或73.
18./
【分析】本题主要考查一次函数的应用,利用题意找出等量关系是解题关键.根据题意结合图象,可得与的距离等于与的距离均为,根据行驶路程与时间的关系,可得两车的速度,设甲出发小时后,两车相距,由题意,得,解出即可完成解答..
【详解】解:由题意并结合图形可得:,
甲的速度:,
乙的速度:,
设甲出发小时后,两车相距,
由题意得:,
解得:,
故答案为:.
19.(1)18,图形见解析;
(2)108;
(3)读书在4本以上的人数大约有108人.
【分析】本题考查扇形统计图,样本估计总体的思想,频数分布等知识,解题的关键是熟练掌握基本知识,理解样本和总体的关系.
(1)由随机调查的九年级40名学生读书数量的数据直接得出m的值;
(2)根据读书数量在C组对应人数求出百分比再乘以360 即可得到对应的圆心角;
(3)利用样本估计总体的思想解决问题即可.
【详解】(1)由条形统计图可得:
(2)解:,,
故答案为:.
(3)解:∵40人中共有名学生读书在4本以上,
∴(人)
答:该校八年级学生读书在4本以上的人数为108人.
20.(1)30,150,
(2)见解析
(3)该校学生一周的课外锻炼时间不足三小时的人数为960人
【分析】
本题考查的是频数(率)分布表与条形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
(1)根据阅读时间为的人数及所占百分比可得,求出总人数,再根据频率、频数、总人数的关系即可求出a、b、n;
(2)根据数据将频数分布直方图补充完整即可;
(3)由总人数乘以时间不足三小时的人数的频率即可.
【详解】(1)解:(人),
,
,
故答案为:30,150,0.24
(2)解:如图所示:
(3)解:(人)
即估算该校学生一周的课外锻炼时间不足三小时的人数为960人.
21.(1)见解析
(2)见解析
(3)
【分析】本题主要考查了坐标与图形变化—中心对称,旋转,割补法求三角形面积:
(1)根据关于原点对称的点横纵坐标都互为相反数得到A、B对应点的位置,然后顺次连接
(2)根据所给旋转方式结合网格的特点得到A、B对应点的位置,然后顺次连接即可;
(3)用所在的长方形面积进去周围三个三角形的面积即可得到答案.
【详解】(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:.
故答案为:.
22.(1)
(2)
【分析】本题考查的是二元一次方程组的解法,一,三象限角平分线上点的坐标特点,熟练的解方程组是解本题的关键.
(1)直接利用加减消元法解方程组即可;
(2)由一,三象限角平分线上的点的横纵坐标相等,再建立方程求解即可.
【详解】(1)解:,
,得,
∴.
将代入①,得.
原方程组的解为:;
(2)∵以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,
∴,
解得:.
23.(1)B,D
(2)不平行,理由见详解
(3)图见详解
【分析】本题主要考查函数图像,解题的关键是理解题意;
(1)根据图像及题意可进行求解;
(2)根据图像可进行求解;
(3)根据题意可直接画出函数图像
【详解】(1)解:图①描绘的场景对应图③中的点B,图②描绘的场景对应图③中的点D;
故答案为B,D;
(2)解:线段与线段不平行;理由是因为兔子在发现自己被乌龟赶超了,速度肯定会有所提升,这样就比刚开始比赛时的速度更快,结合速度、时间和路程是成正比例关系的,速度越快,代表着直线的倾斜度也越陡,所以这两条直线是不会平行的;
(3)解:由题意可得如下图像:
24.(1)甲的速度为
(2)图见解析
(3)甲到地的距离为或.
【分析】本题考查从函数图象获取信息,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)根据图象中的数据可知:甲走了,然后即可计算出甲的速度;
(2)根据图象和(1)中的结果,可以计算出甲到达地用的总的时间,然后即可将图象补充完整;
(3)根据题意可知,存在两种情况,然后计算出即可.
【详解】(1)由图象可得,
甲的速度为:,
即甲的速度为;
(2),
甲到达地用的总的时间为:,
补全的图象如右图所示;
(3)设甲走时,甲、乙两人相距240米,
乙到达地前:,
解得,
则此时甲离地的距离为:;
当乙到达地后,当甲、乙两人相距240米时,此时甲到地的距离就是;
答:当甲、乙两人相距240米时,甲到地的距离为或.
25.(1)见解析
(2)见解析
(3)
【分析】本题考查作图﹣旋转变换、平移变换,熟练掌握旋转的性质、平移的性质是解答本题的关键.
(1)根据平移的性质作图即可.
(2)根据旋转的性质作图即可.
(3)连接,,,相交于点M,则绕点M旋转能得到,即可得出答案.
【详解】(1)如图,即为所求.
(2)如图,即为所求.
(3)连接,,,相交于点M,
则则绕点M旋转能得到
由图可得,旋转中心点M的坐标为.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
