河南省百师联盟2023-2024学年高二4月联考数学试题(含解析)
文档属性
| 名称 | 河南省百师联盟2023-2024学年高二4月联考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 646.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 19:54:12 | ||
图片预览




文档简介
2023-2024学年度高二4月联考
数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
考试时间120分钟,满分150分
一、单项选择题(共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知函数,则
A.1 B. C.2 D.4
2.曲线在点处切线的倾斜角为
A. B. C. D.
3.若根据如下样本数据得到的线性回归方程为,则
x 3 4 5 6 7 8
y 4.0 2.5 0.5 0.5 0.4 0.1
A., B., C., D.,
4.为研究高中生的性别与是否喜欢数学课程之间的关系,运用2×2列联表进行检验,经计算,参考下表,则认为“性别与喜欢数学有关”犯错误的概率不超过
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
A.0.1% B.1% C.99% D.99.9%
5.吹气球时,气球的半径r(单位:dm)与体积V(里位:L)之间的函数关系是,估计时,气球的膨胀率为
A. B. C.1 D.
6.已知数列满足,且,若,则m的值可能为
A.2021 B.2022 C.2023 D.2024
7.若函数的图象上不存在与直线垂直的切线,则实数a的取值范围是
A. B. C. D.
8.函数的图象如图所示,是函数的导函数,令,,,则下列数值排序正确的是
A. B. C. D.
二、多项选择题(共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的.)
9.下列求导运算正确的是
A. B. C. D.
10.已知数列的前n项和为,则“数列为等差数列”的充要条件是
A.当时,(d为常数) B.(k,b为常数)
C.(a,b为常数) D.
11.设t为实数,则直线能作为下列函数图象的切线的有
A. B. C. D.
12.已知数列满足,,设的前n项和为,下列结论正确的是
A.数列是等比数列 B.
C. D.当时,数列是单调递减数列
三、填空题:本题共4小题,每小题5分,共20分.
13.数列中,若,,则 .
14.已知变量y关于x的回归方程为,若对两边取自然对数,可以发现与x线性相关,现有一组数据如下表所示:
x 1 2 3 4 5
y e
则当时,预测y的值为 .
15.在等差数列中,奇数项之和为220,偶数项之和为165,若此数列的项数为10,则此数列的公差为 ;若此数列的项数为奇数,则此数列的中间项是 (前一个空2分,后一个空3分).
16.英国著名物理学家牛顿用“作切线”的方法求函数零点.已知二次函数有两个不相等的实根b,c,其中.在函数图象上横坐标为,的点处作曲线的切线,切线与x轴交点的横坐标为;用代替,重复以上的过程得到;一直下去,得到数列,记,且,,则数列的前n项和 .
四、解答题:本题共6小题,共70分,其中第17题10分,其余均12分。
17.(10分)
已知等差数列的公差为d(),前n项和为,且满足;,,成等比数列.
(1)求数列的通项公式;
(2)设,数列的前n项和为,求.
18.(12分)
在等差数列中,,.
(1)求数列的通项公式;
(2)设,求的值.
19.(12分)
2024年2月23日19时30分,中国航天迎来甲辰龙年首飞.长征五号运载火箭成功将通信技术试验卫星十一号送入预定轨道.竖直向上发射的火箭熄火时上升速度达到100m/s,此后其位移H(单位:m)与时间t(单位;s)近似满足函数关系
(1)分别求火箭在、这些时间段内的平均速度;
(2)求火箭在时的瞬时速度﹔
(3)熄火后多长时间火箭上升速度为0.
20.(12分)
已知函数的图象经过点,且在点A处的切线与直线l:垂直.
(1)求a,b的值;
(2)求经过点且与曲线相切的切线方程.
21.(12分)
近年来,短视频作为以视频为载体的聚合平台,社交属性愈发突出,在用户生活中覆盖面越来越广泛,针对短视频的碎片化缺陷,将短视频剪.接成长视频势必成为一种新的技能.某机构在网上随机对1000人进行了一次市场调研,以决策是否开发将短视频剪接成长视频的APP,得到如下数据:
青年人 中年人 老年人
对短视频剪接成长视频的APP有需求 200 a
对短视频剪接成长视频的APP无需求 150 4b
其中的数据为统计的人数,已知被调研的青年人数为400人.
(1)求a,b的值;
(2)根据小概率值的独立性检验,分析青年人与中老年人对短视频剪接成长视频的APP的需求,是否有差异.
参考公式:,其中.
临界值表;
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
22.(12分)
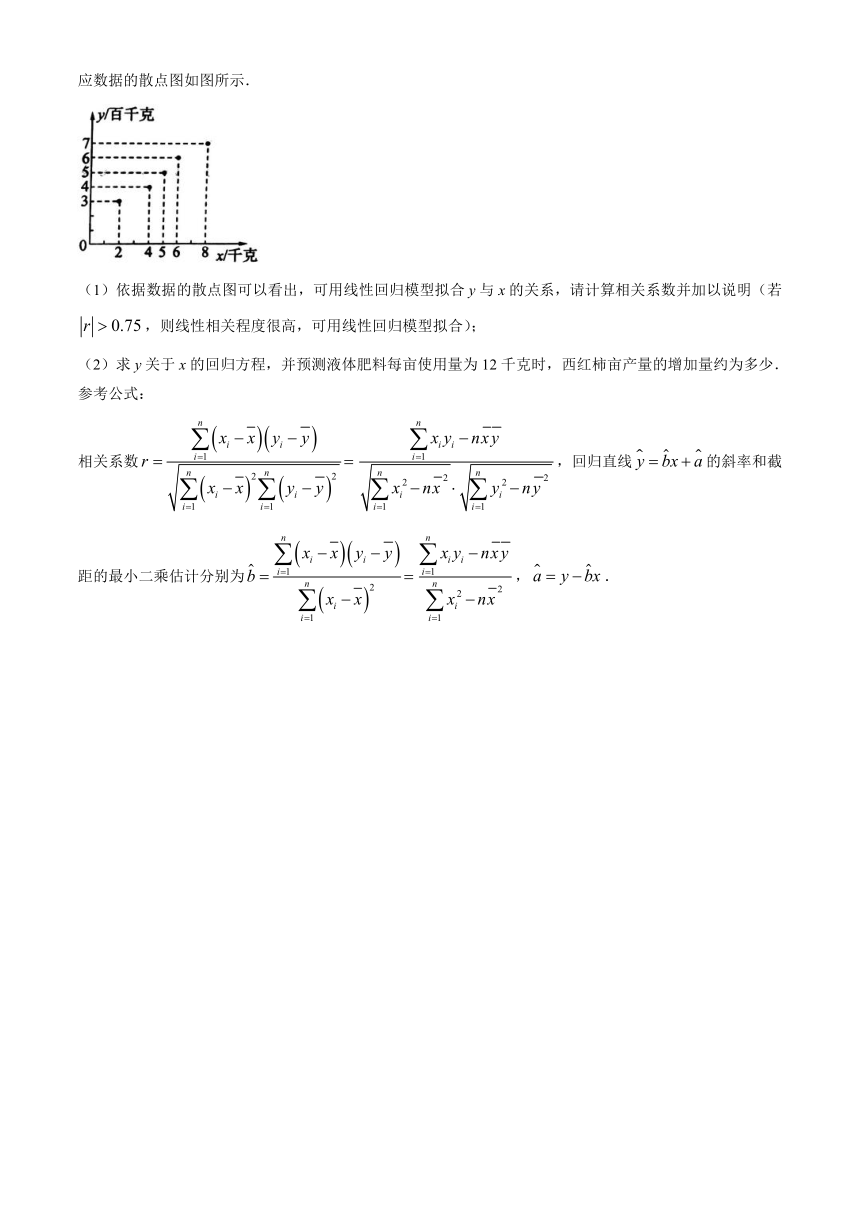
根据统计,某蔬菜基地西红柿亩产量的增加量y(百千克)与某种液体肥料每亩使用量x(千克)之间的对应数据的散点图如图所示.
(1)依据数据的散点图可以看出,可用线性回归模型拟合y与x的关系,请计算相关系数并加以说明(若,则线性相关程度很高,可用线性回归模型拟合);
(2)求y关于x的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量约为多少.
参考公式:
相关系数,回归直线的斜率和截距的最小二乘估计分别为,.
2023—2024学年度高二4月联考
数学参考答案及评分意见
1.A
【解析】,又,则,故选A.
2.C
【解析】,则,故在点处切线的斜率,因为,故.故选C.
3.B
【解析】根据给出的数据可发现:整体上y与x呈现负相关,所以,由样本点及可知.故选B.
4.B
【解析】因为,结合表格可知所以认为“性别与喜欢数学有关”犯错误的概率不超过0.010.故选B.
5.A
【解析】,则,
当时,.故选A.
6.D
【解析】数列的递推公式为,由,
则有,,,,
,则是以4为周期的周期数列,
,有,,故m的值可能为2024,故选D.
7.C
【解析】.
∵函数的图象上不存在与直线垂直的切线,
∴无解,又,
∴,得.故选C.
8.C
【解析】由图象可知在上单调递增,故,即,故选C.
9.CD
【解析】,故A错误;,故B错误;,故C正确;,故D正确.故选CD.
10.BCD
【解析】当时,数列为等差数列,A错误;若数列为等差数列,则,符合的形式,若,则(常数),即数列为等差数列,故数列的通项公式可以表示为数列为等差数列,B正确;若数列为等差数列,则,符合的形式,若有,当时,,当时,符合上式,故,即数列为等差数列,故数列的前n项和可以表示为的形式数列为等差数列,C正确;数列为等差数列,D正确.故选BCD.
11.BC
【解析】
对于A:,故无论x取何值,不可能等于,故A错误﹔
对于B:,令,解得,所以直线能作为该函数图象的切线,故B正确;
对于C:,令,解得,所以直线能作为该函数图象的切线,故C正确;
对于D:,故无论x取何值,不可能等于,故D错误.故选BC.
12.ABD
【解析】
对A:,
且,故数列是等比数列,故A正确;
对B:,,,
由,得,故B正确;.
对于C:因为,
所以,.故C错误.
对D:当时,是单调递减数列,也是单调递减数列,
所以是单调递减数列,故D正确.
故选ABD.
13.19
【解析】∵,∴,∴故数列为等差数列,公差等于2,
∴,故答案为19.
14.
【解析】对两边取对数,得,令,则.
x 1 2 3 4 5
y e
z 1 3 4 6 7
,,
代入得故.
故,.
当时,.
故答案为.
15.;55
【解析】令,,
若此数列的项数为10,则,所以,所以;
若此数列的项数为奇数,设项数为,则
奇数项之和,
偶数项之和,
所以,解得,
所以第4项是此数列的中间项,.
故答案为;55.
16.
【解析】因为二次函数有两个不等实数根b,c,
所以不妨设.
因为,所以,
所以在横坐标为的点处的切线方程为:.
令,则,
因为,
所以,即,
所以数列是公比为2,首项为1的等比数列,
所以,且,
由,所以,
故答案为.
17.解:
(1),得,即.
由,,成等比数列,得,,即.
所以,故.
(2),
∴
.
18.解:
(1)设其公差为d,由题意可得.
解得,,
∴,.
(2)设数列的前n项和为,则由(1)可得,,,
由(1)知,令,得,当时,,
当时,可得,
当时,可得,
因为,所以,
所以.
19.解:
(1)由位移H与时间t近似满足函数关系,
则火箭在这些时间段内的平均速度为;
火箭在这些时间段内的平均速度为:.
(2)由函数,可得,可得,
所以火箭在时的瞬时速度为80m/s.
(3)由,令,即,解得,
熄火后10s火箭上升速度为0.
20.解:
(1)因为,所以.
的图象在点处的切线与直线l:垂直,
∴,
解得.
(2)由(1)知,,
设切点坐标为,
因为,
所以切线方程为.
又切线过点,
所以,
即,
解得或.
所以经过点且与曲线相切的切线方程为或.
21.解:
(1)由题意可得:,
解得.
(2)零假设为:对短视频剪接成长视频APP的需求,青年人与中老年人没有差异.由已知得,如下2×2列联表:
青年人 中年人 合计
对短视频剪接成长视频的APP有需求 300 250 550
对短视频剪接成长视频的APP无需求 100 350 450
合计 400 600 1000
可得,
根据小概率值的独立性检验,我们推断不成立,
所以青年人与中老年人对短视频剪接成长视频的APP的需求有差异.
22.解:
(1),.
,
,
,
所以,
则可用线性回归模型拟合y与x的关系.
(2)由(1)得,
则,所以.
当时,,
所以预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量为990kg.
数学试题
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
考试时间120分钟,满分150分
一、单项选择题(共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知函数,则
A.1 B. C.2 D.4
2.曲线在点处切线的倾斜角为
A. B. C. D.
3.若根据如下样本数据得到的线性回归方程为,则
x 3 4 5 6 7 8
y 4.0 2.5 0.5 0.5 0.4 0.1
A., B., C., D.,
4.为研究高中生的性别与是否喜欢数学课程之间的关系,运用2×2列联表进行检验,经计算,参考下表,则认为“性别与喜欢数学有关”犯错误的概率不超过
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
A.0.1% B.1% C.99% D.99.9%
5.吹气球时,气球的半径r(单位:dm)与体积V(里位:L)之间的函数关系是,估计时,气球的膨胀率为
A. B. C.1 D.
6.已知数列满足,且,若,则m的值可能为
A.2021 B.2022 C.2023 D.2024
7.若函数的图象上不存在与直线垂直的切线,则实数a的取值范围是
A. B. C. D.
8.函数的图象如图所示,是函数的导函数,令,,,则下列数值排序正确的是
A. B. C. D.
二、多项选择题(共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的.)
9.下列求导运算正确的是
A. B. C. D.
10.已知数列的前n项和为,则“数列为等差数列”的充要条件是
A.当时,(d为常数) B.(k,b为常数)
C.(a,b为常数) D.
11.设t为实数,则直线能作为下列函数图象的切线的有
A. B. C. D.
12.已知数列满足,,设的前n项和为,下列结论正确的是
A.数列是等比数列 B.
C. D.当时,数列是单调递减数列
三、填空题:本题共4小题,每小题5分,共20分.
13.数列中,若,,则 .
14.已知变量y关于x的回归方程为,若对两边取自然对数,可以发现与x线性相关,现有一组数据如下表所示:
x 1 2 3 4 5
y e
则当时,预测y的值为 .
15.在等差数列中,奇数项之和为220,偶数项之和为165,若此数列的项数为10,则此数列的公差为 ;若此数列的项数为奇数,则此数列的中间项是 (前一个空2分,后一个空3分).
16.英国著名物理学家牛顿用“作切线”的方法求函数零点.已知二次函数有两个不相等的实根b,c,其中.在函数图象上横坐标为,的点处作曲线的切线,切线与x轴交点的横坐标为;用代替,重复以上的过程得到;一直下去,得到数列,记,且,,则数列的前n项和 .
四、解答题:本题共6小题,共70分,其中第17题10分,其余均12分。
17.(10分)
已知等差数列的公差为d(),前n项和为,且满足;,,成等比数列.
(1)求数列的通项公式;
(2)设,数列的前n项和为,求.
18.(12分)
在等差数列中,,.
(1)求数列的通项公式;
(2)设,求的值.
19.(12分)
2024年2月23日19时30分,中国航天迎来甲辰龙年首飞.长征五号运载火箭成功将通信技术试验卫星十一号送入预定轨道.竖直向上发射的火箭熄火时上升速度达到100m/s,此后其位移H(单位:m)与时间t(单位;s)近似满足函数关系
(1)分别求火箭在、这些时间段内的平均速度;
(2)求火箭在时的瞬时速度﹔
(3)熄火后多长时间火箭上升速度为0.
20.(12分)
已知函数的图象经过点,且在点A处的切线与直线l:垂直.
(1)求a,b的值;
(2)求经过点且与曲线相切的切线方程.
21.(12分)
近年来,短视频作为以视频为载体的聚合平台,社交属性愈发突出,在用户生活中覆盖面越来越广泛,针对短视频的碎片化缺陷,将短视频剪.接成长视频势必成为一种新的技能.某机构在网上随机对1000人进行了一次市场调研,以决策是否开发将短视频剪接成长视频的APP,得到如下数据:
青年人 中年人 老年人
对短视频剪接成长视频的APP有需求 200 a
对短视频剪接成长视频的APP无需求 150 4b
其中的数据为统计的人数,已知被调研的青年人数为400人.
(1)求a,b的值;
(2)根据小概率值的独立性检验,分析青年人与中老年人对短视频剪接成长视频的APP的需求,是否有差异.
参考公式:,其中.
临界值表;
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
22.(12分)
根据统计,某蔬菜基地西红柿亩产量的增加量y(百千克)与某种液体肥料每亩使用量x(千克)之间的对应数据的散点图如图所示.
(1)依据数据的散点图可以看出,可用线性回归模型拟合y与x的关系,请计算相关系数并加以说明(若,则线性相关程度很高,可用线性回归模型拟合);
(2)求y关于x的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量约为多少.
参考公式:
相关系数,回归直线的斜率和截距的最小二乘估计分别为,.
2023—2024学年度高二4月联考
数学参考答案及评分意见
1.A
【解析】,又,则,故选A.
2.C
【解析】,则,故在点处切线的斜率,因为,故.故选C.
3.B
【解析】根据给出的数据可发现:整体上y与x呈现负相关,所以,由样本点及可知.故选B.
4.B
【解析】因为,结合表格可知所以认为“性别与喜欢数学有关”犯错误的概率不超过0.010.故选B.
5.A
【解析】,则,
当时,.故选A.
6.D
【解析】数列的递推公式为,由,
则有,,,,
,则是以4为周期的周期数列,
,有,,故m的值可能为2024,故选D.
7.C
【解析】.
∵函数的图象上不存在与直线垂直的切线,
∴无解,又,
∴,得.故选C.
8.C
【解析】由图象可知在上单调递增,故,即,故选C.
9.CD
【解析】,故A错误;,故B错误;,故C正确;,故D正确.故选CD.
10.BCD
【解析】当时,数列为等差数列,A错误;若数列为等差数列,则,符合的形式,若,则(常数),即数列为等差数列,故数列的通项公式可以表示为数列为等差数列,B正确;若数列为等差数列,则,符合的形式,若有,当时,,当时,符合上式,故,即数列为等差数列,故数列的前n项和可以表示为的形式数列为等差数列,C正确;数列为等差数列,D正确.故选BCD.
11.BC
【解析】
对于A:,故无论x取何值,不可能等于,故A错误﹔
对于B:,令,解得,所以直线能作为该函数图象的切线,故B正确;
对于C:,令,解得,所以直线能作为该函数图象的切线,故C正确;
对于D:,故无论x取何值,不可能等于,故D错误.故选BC.
12.ABD
【解析】
对A:,
且,故数列是等比数列,故A正确;
对B:,,,
由,得,故B正确;.
对于C:因为,
所以,.故C错误.
对D:当时,是单调递减数列,也是单调递减数列,
所以是单调递减数列,故D正确.
故选ABD.
13.19
【解析】∵,∴,∴故数列为等差数列,公差等于2,
∴,故答案为19.
14.
【解析】对两边取对数,得,令,则.
x 1 2 3 4 5
y e
z 1 3 4 6 7
,,
代入得故.
故,.
当时,.
故答案为.
15.;55
【解析】令,,
若此数列的项数为10,则,所以,所以;
若此数列的项数为奇数,设项数为,则
奇数项之和,
偶数项之和,
所以,解得,
所以第4项是此数列的中间项,.
故答案为;55.
16.
【解析】因为二次函数有两个不等实数根b,c,
所以不妨设.
因为,所以,
所以在横坐标为的点处的切线方程为:.
令,则,
因为,
所以,即,
所以数列是公比为2,首项为1的等比数列,
所以,且,
由,所以,
故答案为.
17.解:
(1),得,即.
由,,成等比数列,得,,即.
所以,故.
(2),
∴
.
18.解:
(1)设其公差为d,由题意可得.
解得,,
∴,.
(2)设数列的前n项和为,则由(1)可得,,,
由(1)知,令,得,当时,,
当时,可得,
当时,可得,
因为,所以,
所以.
19.解:
(1)由位移H与时间t近似满足函数关系,
则火箭在这些时间段内的平均速度为;
火箭在这些时间段内的平均速度为:.
(2)由函数,可得,可得,
所以火箭在时的瞬时速度为80m/s.
(3)由,令,即,解得,
熄火后10s火箭上升速度为0.
20.解:
(1)因为,所以.
的图象在点处的切线与直线l:垂直,
∴,
解得.
(2)由(1)知,,
设切点坐标为,
因为,
所以切线方程为.
又切线过点,
所以,
即,
解得或.
所以经过点且与曲线相切的切线方程为或.
21.解:
(1)由题意可得:,
解得.
(2)零假设为:对短视频剪接成长视频APP的需求,青年人与中老年人没有差异.由已知得,如下2×2列联表:
青年人 中年人 合计
对短视频剪接成长视频的APP有需求 300 250 550
对短视频剪接成长视频的APP无需求 100 350 450
合计 400 600 1000
可得,
根据小概率值的独立性检验,我们推断不成立,
所以青年人与中老年人对短视频剪接成长视频的APP的需求有差异.
22.解:
(1),.
,
,
,
所以,
则可用线性回归模型拟合y与x的关系.
(2)由(1)得,
则,所以.
当时,,
所以预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量为990kg.
同课章节目录
