九年级数学下册试题 第二十七章 《圆与正多边形》单元测试卷 -沪教版(含答案)
文档属性
| 名称 | 九年级数学下册试题 第二十七章 《圆与正多边形》单元测试卷 -沪教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 21:26:54 | ||
图片预览


文档简介
第二十七章 《圆与正多边形》单元测试卷
一、选择题(每小题4分,共24分)
1.已知⊙O的直径为6,点P到圆心O的距离为4,则点P在( )
A.⊙O内 B.⊙O外 C.⊙O上 D.无法确定
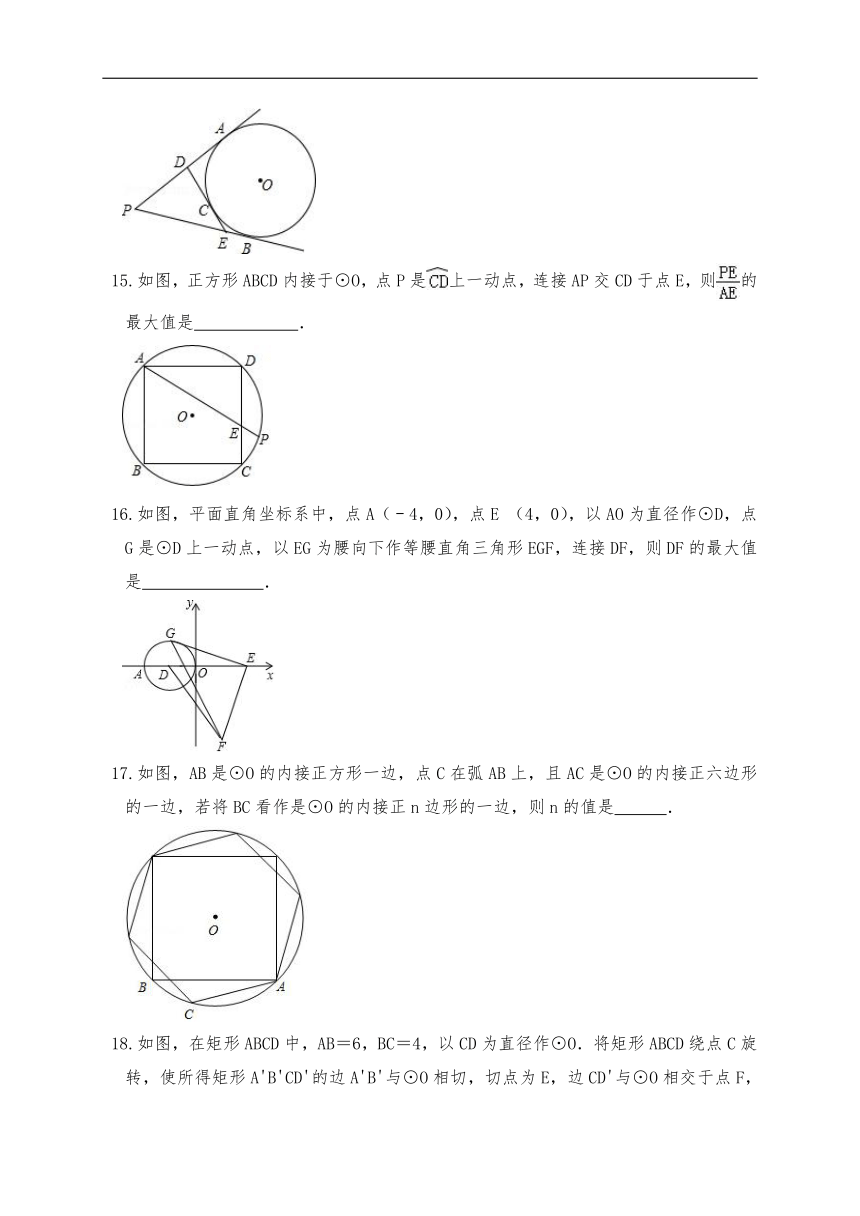
2.直线l与半径为r的⊙O相交,且点O到直线l的距离为3,则r的取值范围是( )
A.r<3 B.r=3 C.r>3 D.r≥3
3.如图,在平行四边形ABCD中,BC=5,S ABCD=10,以顶点C为圆心,BC为半径作圆,则AD边所在直线与⊙C的位置关系是( )
A.相交 B.相切
C.相离 D.以上三种都有可能
4.一个正五边形和一个正六边形按如图方式摆放,它们都有一边在直线l上,且有一个公共顶点O,则∠AOB的度数是( )
A.83° B.84° C.85° D.94°
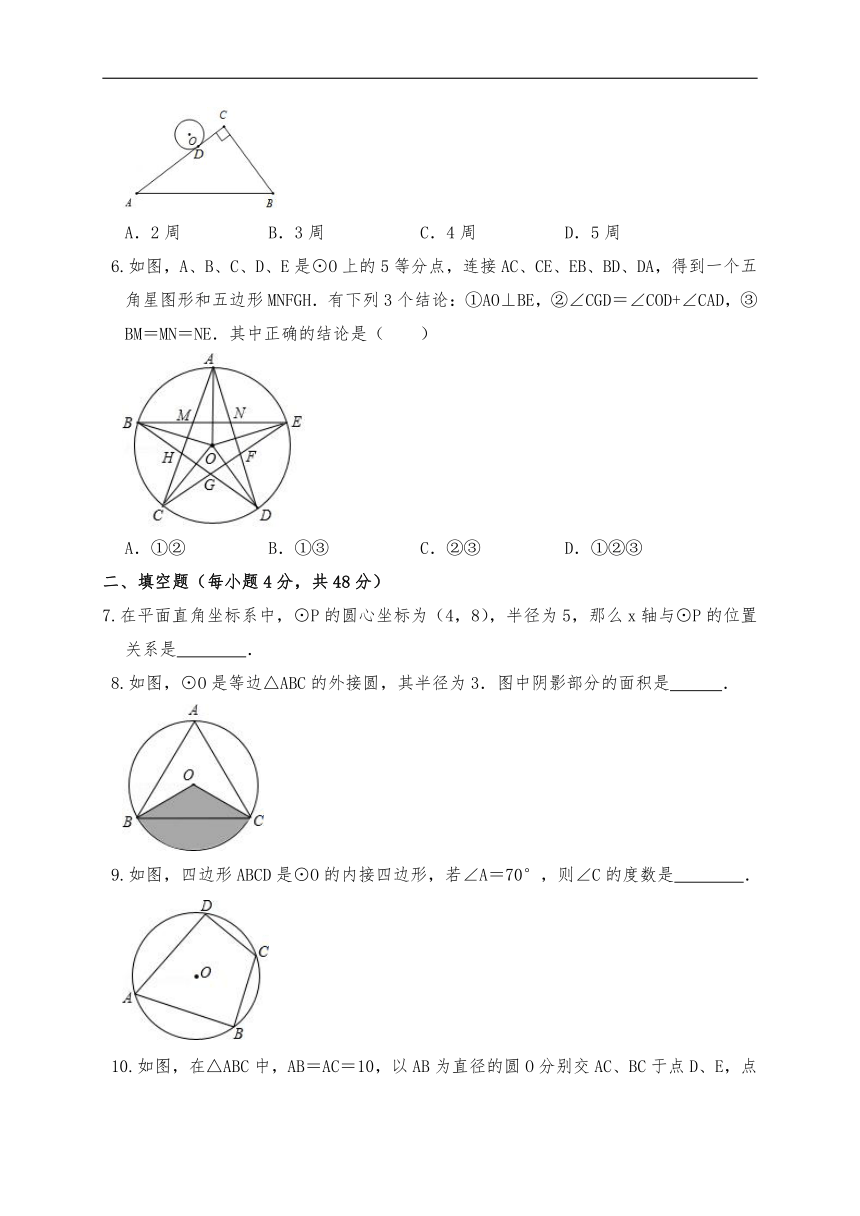
5.如图,Rt△ABC中,∠C=90°,AC=4π,BC=3π,半径是2的⊙O从与AC相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AC相切于点D的位置,则⊙O自转了( )
A.2周 B.3周 C.4周 D.5周
6.如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:①AO⊥BE,②∠CGD=∠COD+∠CAD,③BM=MN=NE.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(每小题4分,共48分)
7.在平面直角坐标系中,⊙P的圆心坐标为(4,8),半径为5,那么x轴与⊙P的位置关系是 .
8.如图,⊙O是等边△ABC的外接圆,其半径为3.图中阴影部分的面积是 .
9.如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是 .
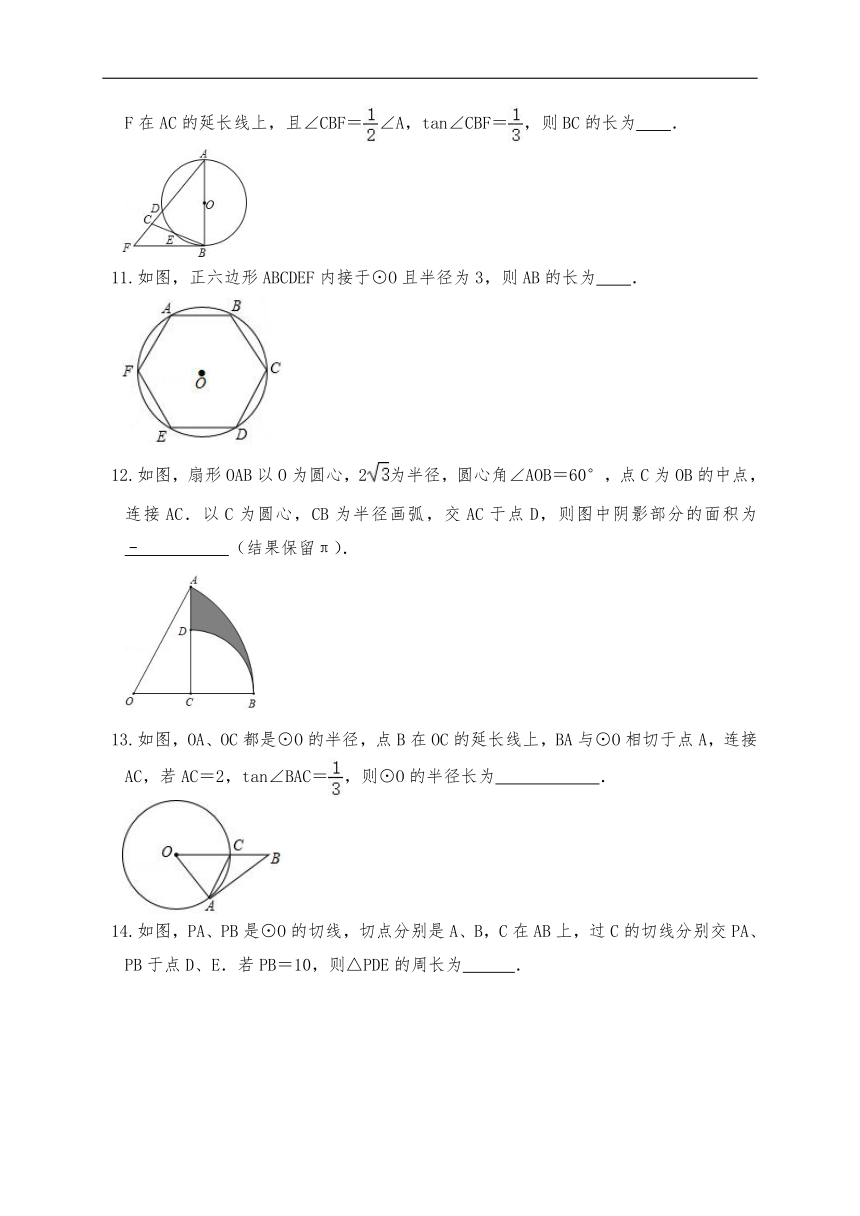
10.如图,在△ABC中,AB=AC=10,以AB为直径的圆O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠A,tan∠CBF=,则BC的长为 .
11.如图,正六边形ABCDEF内接于⊙O且半径为3,则AB的长为 .
12.如图,扇形OAB以O为圆心,2为半径,圆心角∠AOB=60°,点C为OB的中点,连接AC.以C为圆心,CB为半径画弧,交AC于点D,则图中阴影部分的面积为 ﹣ (结果保留π).
13.如图,OA、OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=,则⊙O的半径长为 .
14.如图,PA、PB是⊙O的切线,切点分别是A、B,C在AB上,过C的切线分别交PA、PB于点D、E.若PB=10,则△PDE的周长为 .
15.如图,正方形ABCD内接于⊙O,点P是上一动点,连接AP交CD于点E,则的最大值是 .
16.如图,平面直角坐标系中,点A(﹣4,0),点E (4,0),以AO为直径作⊙D,点G是⊙D上一动点,以EG为腰向下作等腰直角三角形EGF,连接DF,则DF的最大值是 .
17.如图,AB是⊙O的内接正方形一边,点C在弧AB上,且AC是⊙O的内接正六边形的一边,若将BC看作是⊙O的内接正n边形的一边,则n的值是 .
18.如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为 .
三、解答题(共78分)
19.如图,某圆形拱门的拱顶到地面的距离CD=4m,拱门在地面的宽AB=4m,求拱门所在⊙O的半径.
20.如图,BE是⊙O的直径,半径OA⊥弦BC,垂足为D,连接AE、EC.
(1)若∠AEC=25°,求∠AOB的度数;
(2)若∠A=∠B,EC=4,求⊙O的半径.
21.如图,AB是⊙O的直径,点C是⊙O上一点,连接AC、BC,过点C作∠BCP=∠BAC,交AB的延长线于点P,弦CD平分∠ACB,交AB于点E,连接OC、AD、BD.
(1)求证:PC为⊙O的切线;
(2)若OC=5,OE=1,求PC的长.
22.如图,在⊙O中,弦AB⊥弦CD于点E,弦AG⊥弦BC于点F,AG与CD相交于点M.
(1)求证:=;
(2)若弧=80°,⊙O的半径为6,求+的弧长和.
23.如图,已知AB是⊙P的直径,点C在⊙P上,D为⊙P外一点,且∠ADC=90°,直线CD为⊙P的切线.
(1)试说明:2∠B+∠DAB=180°
(2)若∠B=30°,AD=2,求⊙P的半径.
24.如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,并交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,=2,求BG的值.
25.如图,在矩形ABCD中,AB=8cm,AD=6cm,点P从点A出发沿AB以2cm/s的速度向终点B匀速运动,同时点Q从点B出发沿BC以1cm/s的速度向终点C匀速运动,P、Q中有一点到达终点时,另一点随之停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ是直角三角形;
(3)在运动过程中,经过 秒,以P为圆心,AP为半径的⊙P与对角线BD相切.
答案
一、选择题
1.解:∵⊙O的直径为6,
∴⊙O的半径为3,
∵点P到圆心O的距离为4,
∴4>3,
∴点P在⊙O外.
故选:B.
2.解:∵直线l与半径为r的⊙O相交,且点O到直线l的距离为3,
∴r>3,
故选:C.
3.解:如图,作CH⊥DA交DA的延长线于H.
∵S平行四边形ABCD=BC CH,
∴CH==2,
∵2<5,
∴直线AD与⊙C相交,
故选:A.
4.解:由题意:∠AOE=108°,∠BOF=120°,∠OEF=72°,∠OFE=60°,
∴∠EOF=180°﹣72°﹣60°=48°,
∴∠AOB=360°﹣108°﹣48°﹣120°=84°,
故选:B.
5.解:Rt△ABC中,AC=4π,BC=3π,
∴AB=5π,
圆在三边运动自转周数:=3,
圆绕过三角形外角时,共自转了三角形外角和的度数:360°,即一周;
可见,⊙O自转了3+1=4周.
故选:C.
6.解:∵A、B、C、D、E是⊙O上的5等分点,
∴=,
∴AO⊥BE,故①正确;
∵A、B、C、D、E是⊙O上的5等分点,
∴的度数==72°
∴∠COD=72°
∵∠COD=2∠CAD
∴∠CAD=36°;
连接CD
∵A、B、C、D、E是⊙O上的5等分点,
∴===,
∴∠BDC=∠DCE=∠CAD=36°,
∴∠CGD=108°,
∴∠CGD=∠COD+∠CAD,故②正确;
连接AB,AE,
则∠BAM=∠ABM=∠EAN=∠AEN=36°,
∵AB=AE,
∴△ABM≌△AEN(ASA),
∴BM=EN=AM=AN,
∵∠MAN=36°,
∴AM≠MN,③错误.
故选:A.
二、填空题
7.解:在直角坐标系内,以P(4,8)为圆心,5为半径画圆,则点P到x轴的距离为d=8,
∵r=5,
∴d>r,
∴⊙P与x轴的相离.
故答案为:相离.
8.解:∵△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴图中阴影部分的面积==3π,
故答案为:3π.
9.解:∵四边形ABCD是⊙O的内接四边形,
∴∠C+∠A=180°,
∴∠C=180°﹣70°=110°.
故答案为:110°.
10.解:连接AE,如图,
∵AB为直径,
∴∠AEB=90°,
∵AB=AC,
∴AE平分∠BAC,BE=CE,
即∠BAE=∠BAC,
∵∠CBF=∠BAC,
∴∠CBF=∠BAE,
∴tan∠BAE=tan∠CBF=,
在Rt△ABE中,tan∠BAE==,
设BE=x,则AE=3x,
∴AB==x,
即x=10,解得x=,
∴BC=2BE=2x=2.
故答案为2.
11.解:连接OA、OB,如图所示:
∵正六边形ABCDEF内接于⊙O,
∴∠AOB==60°,
∵OA=OB=3,
∴△AOB是等边三角形,
∴AB=OA=OB=3,
故答案为:3.
12.解:连接AB,
∵OA=OB,∠AOB=60°,
∴△AOB为等边三角形,
∵点C为OB的中点,
∴OC=BC=,AC⊥OB,
由勾股定理得,AC===3,
∴图中阴影部分的面积=﹣××3﹣=π﹣,
故答案为:π﹣.
13.解:作直径AD,连接CD,如图,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠DAC=90°,
∵BA与⊙O相切于点A,
∴OA⊥AB,
∴∠DAB=90°,即∠DAC+∠BAC=90°,
∴∠D=∠BAC,
∴tanD=tan∠BAC=,
在Rt△ACD中,tanD=,即=,解得CD=6,
∴AD==2,
∴⊙O的半径长为,
故答案为:.
14.解:∵PA、PB、DE是圆O的切线,切点分别是A、B、C,
∴AP=BP,DA=DC,CE=BE,
∴△PED的周长是:PD+DE+PE
=PD+DC+CE+PE
=PD+DA+PE+BE
=PA+PB
=2PB=20.
答:△PED的周长是20.
故答案为:20.
15.解:过P作PQ⊥CD于Q,
∵四边形ABCD是正方形,
∴∠ADC=90°,
∴AD∥PQ,
∴△ADE∽△PQE,
∴=,
∴取最大值时,即取最大值,
∵AD一定,
∴当PQ取最大值时,的值最大,
∴当P为的中点时,PQ 最大,
延长PQ交⊙O于另一点于M,
则PM为⊙O的直径,
设正方形的边长为a,则PM=AC=a,
∴PQ=(a﹣a),
∴的最大值===,
故答案为:.
16.解:如图,连接DG,过点E作EH⊥AE,且DE=EH,连接DH,FH,
∵点A(﹣4,0),点E (4,0),
∴AO=4=OE,
∵AO是圆D直径,
∴DO=AO=2,
∴DE=6=EH,且EH⊥AE,
∴DH=6,
∵等腰直角三角形EGF,
∴GE=EF,∠GEF=∠DEH=90°,
∴∠GED=∠FEH,且GE=EF,DE=EH,
∴△GDE≌△HFE(SAS)
∴GD=FH=2,
∴点F在以H为圆心,2为半径的圆上,
∴当点F在DH的延长线上时,DF有最大值,
∴DF的最大值为6+2,
故答案为:6+2.
17.解:连接OC,
∵AB是⊙O内接正方形的一边,
∴∠AOB=360°÷4=90°,
∵BC是⊙O内接正六边形的一边,
∴∠BOC=360°÷6=60°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°,
∴n=360°÷30°=12;
故答案为:12;
18.解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=6,BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=3,
∴B′H=OE=3,
∴CH=B′C﹣B′H=1,
∴CG=B′E=OH==2,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故答案为:4.
三、解答题
19.解:连接OA,
设OA=x,则OC=x,
∵CD=4m,
∴OD=(4﹣x)m,
∵CD⊥AB,
∴AD=AB=×4=2m,
OA2=OD2+AD2,
∴x2=(4﹣x)2+22,
解得:x=2.5,
故拱门所在⊙O的半径为2.5.
20.解:(1)连接OC.
∵半径OA⊥弦BC,
∴,
∴∠AOC=∠AOB,
∵∠AOC=2∠AEC=50°,
∴∠AOB=50°.
(2)∵BE是⊙O的直径,
∴∠ECB=90°,
∴EC⊥BC,
∵OA⊥BC,
∴EC∥OA,
∴∠A=∠AEC,
∵OA=OE,
∴∠A=∠OEA,
∵∠A=∠B,
∴∠B=∠AEB=∠AEC=30°,
∵EC=4,
∴EB=2EC=8,
∴⊙O的半径为4.
21.(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∵AB是⊙O的直径,
∴∠ACB=90°
∴∠BAC+∠OBC=90°,
∵∠BCP=∠BAC,
∴∠OCB+∠BCP=90°,即∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)解:∵CD平分∠ACB,
∴∠ACD=∠BCD
∴=,
∴∠ABD=∠DCB,
∵∠BCP=∠BAC,∠BAC=∠BDC,∠BAD=∠BCD,
∴∠PCB=∠BDC,∠ABD=∠BCD,
∴∠BDC+∠ABD=∠BCD+∠PCB,即∠PEC=∠PCE,
∴PC=PE,
设PC=PE=x,则OP=x+1,
在Rt△OPC中,OP2=OC2+PC2,
∴(x+1)2=52+x2,
解得x=12,
∴PC=12.
22.(1)证明:∵AB⊥CD,AG⊥BC,
∴∠DCB+∠B=90°,∠GAB+∠B=90°,
∴∠DCB=∠GAB,
∴;
(2)∵的度数是80°,
∴∠B=40°,
∴∠DCB=50°,
∴∠GMC=40°,
∴∠ACD+∠CAG=40°,
23.解:(1)连接CP,
∵PC=PB,
∴∠B=∠PCB,
∴∠APC=∠PCB+∠B=2∠B,
∵CD是⊙OP的切线,
∴∠DCP=90°,
∵∠ADC=90°,
∴∠DAB+∠APC=180°
∴2∠B+∠DAB=180°;
(2)解:连接AC,
∵∠B=30°,
∴∠APC=60°,
∵PC=PA,
∴△ACP是等边三角形,
∴AC=PA,∠ACP=60°,
∴∠ACD=30°,
∴AC=2AD=4,
∴PA=4.
即⊙P的半径为4.
24.解:(1)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠B=45°,
∴∠COE=2∠B=90°,
∵EF是⊙O的切线,
∴∠FEO=90°,
∴EF∥OC,
∵DE∥CF,
∴四边形CDEF是平行四边形;
(2)过G作GN⊥BC于N.
∴△GNB是等腰直角三角形,
∴NB=GN,
∵四边形CDEF是平行四边形,
∴∠FCD=∠FED,
∵∠ACD+∠GCB=∠GCB+∠CGN=90°,
∴∠CGN=∠ACD,
∴∠CGN=∠DEF,
∵=2,
∴tan∠EDO=tan∠CGN==2,
∴CN=2GN,
∴CN+BN=2GN+GN=3,
∴GN=1,
∴BG=GN=.
25.解:(1)设t秒后点P、D的距离是点P、Q距离的2倍,
∴PD=2PQ,∴PD2=4 PQ2,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
∴PD2=AP2+AD2,PQ2=BP2+BQ2,
∵PD2=4 PQ2,
∴62+(2t)2=4[(8﹣2t)2+t2],
解得:t1=,t2=;
∵0≤t≤4,
∴t=,
答:秒后,点P、D的距离是点P、Q的距离的2倍;
(2)∵△DPQ是直角三角形,
∴∠DPQ=90°或∠DQP=90°.
当∠DPQ=90°时,∠ADP=∠BPQ,
∴tan∠ADP=tan∠BPQ,
∴=,即=,
解得:t=,或t=0(舍去);
当∠DQP=90°时,∠CDQ=∠BQP,
∴tan∠CDQ=tan∠BQP,
∴=,
即=,
解得:t=11﹣,或t=11+(舍去),
综上所述,当运动时间为秒或(11﹣)秒时,△DPQ是直角三角形.
(3)设经过x,秒以P为圆心,AP为半径的⊙P与对角线BD相切于点E,连接PE、PD,如图所示:
则PE⊥BD,PE=AP,
在Rt△APD和Rt△EPD中,,
∴Rt△APD≌Rt△EPD(HL),
∴AD=ED=6,
∵BD===10,
∴BE=BD﹣ED=4,
∵PE=PA=2x,则BP=8﹣2x,
在Rt△BPE中,由勾股定理得:(2x)2+42=(8﹣2x)2,
解得:x=,
即经过秒,以P为圆心,AP为半径的⊙P与对角线BD相切,
故答案为:.
一、选择题(每小题4分,共24分)
1.已知⊙O的直径为6,点P到圆心O的距离为4,则点P在( )
A.⊙O内 B.⊙O外 C.⊙O上 D.无法确定
2.直线l与半径为r的⊙O相交,且点O到直线l的距离为3,则r的取值范围是( )
A.r<3 B.r=3 C.r>3 D.r≥3
3.如图,在平行四边形ABCD中,BC=5,S ABCD=10,以顶点C为圆心,BC为半径作圆,则AD边所在直线与⊙C的位置关系是( )
A.相交 B.相切
C.相离 D.以上三种都有可能
4.一个正五边形和一个正六边形按如图方式摆放,它们都有一边在直线l上,且有一个公共顶点O,则∠AOB的度数是( )
A.83° B.84° C.85° D.94°
5.如图,Rt△ABC中,∠C=90°,AC=4π,BC=3π,半径是2的⊙O从与AC相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AC相切于点D的位置,则⊙O自转了( )
A.2周 B.3周 C.4周 D.5周
6.如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:①AO⊥BE,②∠CGD=∠COD+∠CAD,③BM=MN=NE.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(每小题4分,共48分)
7.在平面直角坐标系中,⊙P的圆心坐标为(4,8),半径为5,那么x轴与⊙P的位置关系是 .
8.如图,⊙O是等边△ABC的外接圆,其半径为3.图中阴影部分的面积是 .
9.如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是 .
10.如图,在△ABC中,AB=AC=10,以AB为直径的圆O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠A,tan∠CBF=,则BC的长为 .
11.如图,正六边形ABCDEF内接于⊙O且半径为3,则AB的长为 .
12.如图,扇形OAB以O为圆心,2为半径,圆心角∠AOB=60°,点C为OB的中点,连接AC.以C为圆心,CB为半径画弧,交AC于点D,则图中阴影部分的面积为 ﹣ (结果保留π).
13.如图,OA、OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=,则⊙O的半径长为 .
14.如图,PA、PB是⊙O的切线,切点分别是A、B,C在AB上,过C的切线分别交PA、PB于点D、E.若PB=10,则△PDE的周长为 .
15.如图,正方形ABCD内接于⊙O,点P是上一动点,连接AP交CD于点E,则的最大值是 .
16.如图,平面直角坐标系中,点A(﹣4,0),点E (4,0),以AO为直径作⊙D,点G是⊙D上一动点,以EG为腰向下作等腰直角三角形EGF,连接DF,则DF的最大值是 .
17.如图,AB是⊙O的内接正方形一边,点C在弧AB上,且AC是⊙O的内接正六边形的一边,若将BC看作是⊙O的内接正n边形的一边,则n的值是 .
18.如图,在矩形ABCD中,AB=6,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为 .
三、解答题(共78分)
19.如图,某圆形拱门的拱顶到地面的距离CD=4m,拱门在地面的宽AB=4m,求拱门所在⊙O的半径.
20.如图,BE是⊙O的直径,半径OA⊥弦BC,垂足为D,连接AE、EC.
(1)若∠AEC=25°,求∠AOB的度数;
(2)若∠A=∠B,EC=4,求⊙O的半径.
21.如图,AB是⊙O的直径,点C是⊙O上一点,连接AC、BC,过点C作∠BCP=∠BAC,交AB的延长线于点P,弦CD平分∠ACB,交AB于点E,连接OC、AD、BD.
(1)求证:PC为⊙O的切线;
(2)若OC=5,OE=1,求PC的长.
22.如图,在⊙O中,弦AB⊥弦CD于点E,弦AG⊥弦BC于点F,AG与CD相交于点M.
(1)求证:=;
(2)若弧=80°,⊙O的半径为6,求+的弧长和.
23.如图,已知AB是⊙P的直径,点C在⊙P上,D为⊙P外一点,且∠ADC=90°,直线CD为⊙P的切线.
(1)试说明:2∠B+∠DAB=180°
(2)若∠B=30°,AD=2,求⊙P的半径.
24.如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,并交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,=2,求BG的值.
25.如图,在矩形ABCD中,AB=8cm,AD=6cm,点P从点A出发沿AB以2cm/s的速度向终点B匀速运动,同时点Q从点B出发沿BC以1cm/s的速度向终点C匀速运动,P、Q中有一点到达终点时,另一点随之停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ是直角三角形;
(3)在运动过程中,经过 秒,以P为圆心,AP为半径的⊙P与对角线BD相切.
答案
一、选择题
1.解:∵⊙O的直径为6,
∴⊙O的半径为3,
∵点P到圆心O的距离为4,
∴4>3,
∴点P在⊙O外.
故选:B.
2.解:∵直线l与半径为r的⊙O相交,且点O到直线l的距离为3,
∴r>3,
故选:C.
3.解:如图,作CH⊥DA交DA的延长线于H.
∵S平行四边形ABCD=BC CH,
∴CH==2,
∵2<5,
∴直线AD与⊙C相交,
故选:A.
4.解:由题意:∠AOE=108°,∠BOF=120°,∠OEF=72°,∠OFE=60°,
∴∠EOF=180°﹣72°﹣60°=48°,
∴∠AOB=360°﹣108°﹣48°﹣120°=84°,
故选:B.
5.解:Rt△ABC中,AC=4π,BC=3π,
∴AB=5π,
圆在三边运动自转周数:=3,
圆绕过三角形外角时,共自转了三角形外角和的度数:360°,即一周;
可见,⊙O自转了3+1=4周.
故选:C.
6.解:∵A、B、C、D、E是⊙O上的5等分点,
∴=,
∴AO⊥BE,故①正确;
∵A、B、C、D、E是⊙O上的5等分点,
∴的度数==72°
∴∠COD=72°
∵∠COD=2∠CAD
∴∠CAD=36°;
连接CD
∵A、B、C、D、E是⊙O上的5等分点,
∴===,
∴∠BDC=∠DCE=∠CAD=36°,
∴∠CGD=108°,
∴∠CGD=∠COD+∠CAD,故②正确;
连接AB,AE,
则∠BAM=∠ABM=∠EAN=∠AEN=36°,
∵AB=AE,
∴△ABM≌△AEN(ASA),
∴BM=EN=AM=AN,
∵∠MAN=36°,
∴AM≠MN,③错误.
故选:A.
二、填空题
7.解:在直角坐标系内,以P(4,8)为圆心,5为半径画圆,则点P到x轴的距离为d=8,
∵r=5,
∴d>r,
∴⊙P与x轴的相离.
故答案为:相离.
8.解:∵△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴图中阴影部分的面积==3π,
故答案为:3π.
9.解:∵四边形ABCD是⊙O的内接四边形,
∴∠C+∠A=180°,
∴∠C=180°﹣70°=110°.
故答案为:110°.
10.解:连接AE,如图,
∵AB为直径,
∴∠AEB=90°,
∵AB=AC,
∴AE平分∠BAC,BE=CE,
即∠BAE=∠BAC,
∵∠CBF=∠BAC,
∴∠CBF=∠BAE,
∴tan∠BAE=tan∠CBF=,
在Rt△ABE中,tan∠BAE==,
设BE=x,则AE=3x,
∴AB==x,
即x=10,解得x=,
∴BC=2BE=2x=2.
故答案为2.
11.解:连接OA、OB,如图所示:
∵正六边形ABCDEF内接于⊙O,
∴∠AOB==60°,
∵OA=OB=3,
∴△AOB是等边三角形,
∴AB=OA=OB=3,
故答案为:3.
12.解:连接AB,
∵OA=OB,∠AOB=60°,
∴△AOB为等边三角形,
∵点C为OB的中点,
∴OC=BC=,AC⊥OB,
由勾股定理得,AC===3,
∴图中阴影部分的面积=﹣××3﹣=π﹣,
故答案为:π﹣.
13.解:作直径AD,连接CD,如图,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠DAC=90°,
∵BA与⊙O相切于点A,
∴OA⊥AB,
∴∠DAB=90°,即∠DAC+∠BAC=90°,
∴∠D=∠BAC,
∴tanD=tan∠BAC=,
在Rt△ACD中,tanD=,即=,解得CD=6,
∴AD==2,
∴⊙O的半径长为,
故答案为:.
14.解:∵PA、PB、DE是圆O的切线,切点分别是A、B、C,
∴AP=BP,DA=DC,CE=BE,
∴△PED的周长是:PD+DE+PE
=PD+DC+CE+PE
=PD+DA+PE+BE
=PA+PB
=2PB=20.
答:△PED的周长是20.
故答案为:20.
15.解:过P作PQ⊥CD于Q,
∵四边形ABCD是正方形,
∴∠ADC=90°,
∴AD∥PQ,
∴△ADE∽△PQE,
∴=,
∴取最大值时,即取最大值,
∵AD一定,
∴当PQ取最大值时,的值最大,
∴当P为的中点时,PQ 最大,
延长PQ交⊙O于另一点于M,
则PM为⊙O的直径,
设正方形的边长为a,则PM=AC=a,
∴PQ=(a﹣a),
∴的最大值===,
故答案为:.
16.解:如图,连接DG,过点E作EH⊥AE,且DE=EH,连接DH,FH,
∵点A(﹣4,0),点E (4,0),
∴AO=4=OE,
∵AO是圆D直径,
∴DO=AO=2,
∴DE=6=EH,且EH⊥AE,
∴DH=6,
∵等腰直角三角形EGF,
∴GE=EF,∠GEF=∠DEH=90°,
∴∠GED=∠FEH,且GE=EF,DE=EH,
∴△GDE≌△HFE(SAS)
∴GD=FH=2,
∴点F在以H为圆心,2为半径的圆上,
∴当点F在DH的延长线上时,DF有最大值,
∴DF的最大值为6+2,
故答案为:6+2.
17.解:连接OC,
∵AB是⊙O内接正方形的一边,
∴∠AOB=360°÷4=90°,
∵BC是⊙O内接正六边形的一边,
∴∠BOC=360°÷6=60°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣60°=30°,
∴n=360°÷30°=12;
故答案为:12;
18.解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=6,BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=3,
∴B′H=OE=3,
∴CH=B′C﹣B′H=1,
∴CG=B′E=OH==2,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故答案为:4.
三、解答题
19.解:连接OA,
设OA=x,则OC=x,
∵CD=4m,
∴OD=(4﹣x)m,
∵CD⊥AB,
∴AD=AB=×4=2m,
OA2=OD2+AD2,
∴x2=(4﹣x)2+22,
解得:x=2.5,
故拱门所在⊙O的半径为2.5.
20.解:(1)连接OC.
∵半径OA⊥弦BC,
∴,
∴∠AOC=∠AOB,
∵∠AOC=2∠AEC=50°,
∴∠AOB=50°.
(2)∵BE是⊙O的直径,
∴∠ECB=90°,
∴EC⊥BC,
∵OA⊥BC,
∴EC∥OA,
∴∠A=∠AEC,
∵OA=OE,
∴∠A=∠OEA,
∵∠A=∠B,
∴∠B=∠AEB=∠AEC=30°,
∵EC=4,
∴EB=2EC=8,
∴⊙O的半径为4.
21.(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∵AB是⊙O的直径,
∴∠ACB=90°
∴∠BAC+∠OBC=90°,
∵∠BCP=∠BAC,
∴∠OCB+∠BCP=90°,即∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)解:∵CD平分∠ACB,
∴∠ACD=∠BCD
∴=,
∴∠ABD=∠DCB,
∵∠BCP=∠BAC,∠BAC=∠BDC,∠BAD=∠BCD,
∴∠PCB=∠BDC,∠ABD=∠BCD,
∴∠BDC+∠ABD=∠BCD+∠PCB,即∠PEC=∠PCE,
∴PC=PE,
设PC=PE=x,则OP=x+1,
在Rt△OPC中,OP2=OC2+PC2,
∴(x+1)2=52+x2,
解得x=12,
∴PC=12.
22.(1)证明:∵AB⊥CD,AG⊥BC,
∴∠DCB+∠B=90°,∠GAB+∠B=90°,
∴∠DCB=∠GAB,
∴;
(2)∵的度数是80°,
∴∠B=40°,
∴∠DCB=50°,
∴∠GMC=40°,
∴∠ACD+∠CAG=40°,
23.解:(1)连接CP,
∵PC=PB,
∴∠B=∠PCB,
∴∠APC=∠PCB+∠B=2∠B,
∵CD是⊙OP的切线,
∴∠DCP=90°,
∵∠ADC=90°,
∴∠DAB+∠APC=180°
∴2∠B+∠DAB=180°;
(2)解:连接AC,
∵∠B=30°,
∴∠APC=60°,
∵PC=PA,
∴△ACP是等边三角形,
∴AC=PA,∠ACP=60°,
∴∠ACD=30°,
∴AC=2AD=4,
∴PA=4.
即⊙P的半径为4.
24.解:(1)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠B=45°,
∴∠COE=2∠B=90°,
∵EF是⊙O的切线,
∴∠FEO=90°,
∴EF∥OC,
∵DE∥CF,
∴四边形CDEF是平行四边形;
(2)过G作GN⊥BC于N.
∴△GNB是等腰直角三角形,
∴NB=GN,
∵四边形CDEF是平行四边形,
∴∠FCD=∠FED,
∵∠ACD+∠GCB=∠GCB+∠CGN=90°,
∴∠CGN=∠ACD,
∴∠CGN=∠DEF,
∵=2,
∴tan∠EDO=tan∠CGN==2,
∴CN=2GN,
∴CN+BN=2GN+GN=3,
∴GN=1,
∴BG=GN=.
25.解:(1)设t秒后点P、D的距离是点P、Q距离的2倍,
∴PD=2PQ,∴PD2=4 PQ2,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
∴PD2=AP2+AD2,PQ2=BP2+BQ2,
∵PD2=4 PQ2,
∴62+(2t)2=4[(8﹣2t)2+t2],
解得:t1=,t2=;
∵0≤t≤4,
∴t=,
答:秒后,点P、D的距离是点P、Q的距离的2倍;
(2)∵△DPQ是直角三角形,
∴∠DPQ=90°或∠DQP=90°.
当∠DPQ=90°时,∠ADP=∠BPQ,
∴tan∠ADP=tan∠BPQ,
∴=,即=,
解得:t=,或t=0(舍去);
当∠DQP=90°时,∠CDQ=∠BQP,
∴tan∠CDQ=tan∠BQP,
∴=,
即=,
解得:t=11﹣,或t=11+(舍去),
综上所述,当运动时间为秒或(11﹣)秒时,△DPQ是直角三角形.
(3)设经过x,秒以P为圆心,AP为半径的⊙P与对角线BD相切于点E,连接PE、PD,如图所示:
则PE⊥BD,PE=AP,
在Rt△APD和Rt△EPD中,,
∴Rt△APD≌Rt△EPD(HL),
∴AD=ED=6,
∵BD===10,
∴BE=BD﹣ED=4,
∵PE=PA=2x,则BP=8﹣2x,
在Rt△BPE中,由勾股定理得:(2x)2+42=(8﹣2x)2,
解得:x=,
即经过秒,以P为圆心,AP为半径的⊙P与对角线BD相切,
故答案为:.
