6.3 球的表面积和体积 课件(共22张PPT)-2023-2024学年高一下学期数学北师大版(2019)必修第二册
文档属性
| 名称 | 6.3 球的表面积和体积 课件(共22张PPT)-2023-2024学年高一下学期数学北师大版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 20:15:44 | ||
图片预览








文档简介
(共22张PPT)
第六章 立体几何初步
6.3 球的表面积和体积
同学们,你能列举我们生活中的球吗?
小至微观粒子,大至宇宙星体......
情境引入
在地球模拟实验室的科普展厅,悬挂着直径3米、清晰度达到5K的LED球形屏,装置模拟实验的部分结果会通过球体进行可视化直观展示.
把地球搬进实验室?
其核心软件模拟大气圈、水圈、冰冻圈、岩石圈、生物圈的演变规律,对地球的过去进行反演、对现在进行观察、对未来进行预测.
2021年6月23日,国家重大科技基础设施“地球模拟装置”——寰,在北京怀柔科学城东区落成启用,这是我国首个研制成功的地球系统数值模拟大科学装置.
展厅中这个直径3米LED球形屏上风起云涌,颇为壮观.它究竟有多大,占据多大空间?表面积多少呢?
探索新知——球的截面
探究一 球的截面
类比
1.一条直线与圆相交,在圆内的部分是线段——弦?
用一个平面去截球,得到的截面是什么?
圆面
用一个平面去截球面,得到的截面是什么?
圆
什么情况下,得到的圆最大?
2.直线过圆心时,得到的弦最长——直径.
探索新知——球的截面
球的大圆:球面被经过球心的平面截得的圆.
一 大小圆的定义
球的小圆:球面被不经过球心的平面截得的圆.
探索新知——球的截面
探究一 球的截面
类比
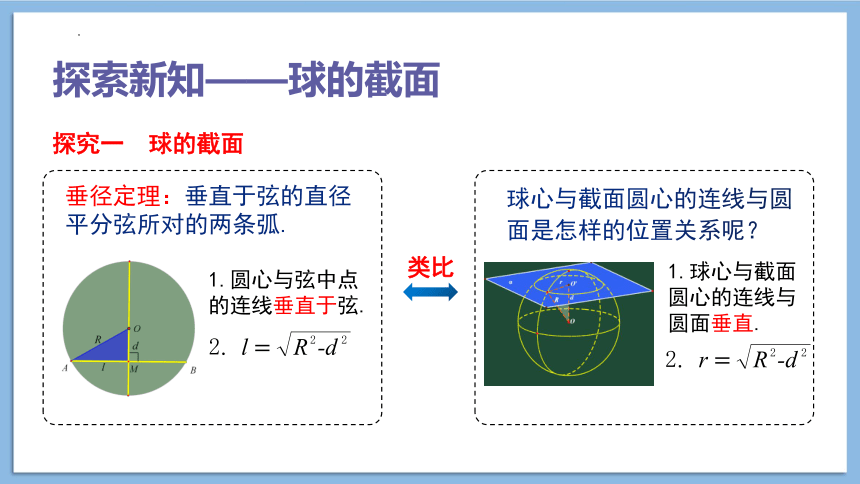
垂径定理:垂直于弦的直径平分弦所对的两条弧.
1.圆心与弦中点的连线垂直于弦.
球心与截面圆心的连线与圆面是怎样的位置关系呢?
1.球心与截面圆心的连线与圆面垂直.
探索新知——球的切线
探究二 球的切线
类比
1.直线与圆有唯一公共点时,叫做直线与圆相切.
2.过圆外一点可以引2条直线与圆相切,且切线长相等.
1.球的切线怎样定义?
2.过球外一点P,可以引多少条直线与球相切?
3.这些切线的长度相等吗?所有切点组成什么图形?
探索新知——球的体积和表面积
探究三 球的表面积和体积
(1)球的表面积:能否采用展开的方法,求球体的表面积呢?
(2)球的体积:给你一个半径为R的实心铁球,如何测量该球的体积呢?
思考:当球的半径变化时,球的体积随之改变,你是否每次都要这样测量呢?
不能,球体无法展开为一个平面图形
排水法
H
R
h
延伸阅读——祖暅原理
“幂势既同,则积不容异”
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
课后探究:查阅资料,阿基米德是如何推算出球体体积的?如何推导求球的表面积计算公式?
延伸阅读——祖暅原理
五 球的表面积和体积计算公式
探索新知——球的体积和表面积
O R
思考:计算球的表面积与体积,关键需要确定哪个量?
例题讲解——初步应用
例2 如图,一个圆锥形的空杯子上面放着一个半球形的冰激凌,如果冰激凌融化了,会溢出杯子吗?(假设冰激凌融化前后体积不变)
例题讲解——初步应用
O’
∟
R
例题讲解——巩固提升
变式训练2 如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为 .
∟
O
O’
A
例题讲解——巩固提升
过点O作OO’ 该截面交于点O’,
OA=R,故(R-2)2+42=R2,解得R=5 cm.
分析:设球半径为R,正方体容器上底正方形所在平面截球所得截面为圆面,
易知Rt△OO’A中,OO’=R-2,O’A=4,
数学思想
概念
课堂小结
球的表面积和体积
球的截面性质、切线性质
球的表面积和体积计算公式的应用
了解祖暅原理及其相关证明
数学建模、数形结合思想
类比思想、转化和化归思想
作业布置
选做题:教材第252页复习题六 B组第10题.
必做题:教材第244页练习3,同步练习册.
板书设计
6.3《球的表面积和体积》
相关性质: 公式: 投影区域
例题讲解:
谢 谢!
第六章 立体几何初步
6.3 球的表面积和体积
同学们,你能列举我们生活中的球吗?
小至微观粒子,大至宇宙星体......
情境引入
在地球模拟实验室的科普展厅,悬挂着直径3米、清晰度达到5K的LED球形屏,装置模拟实验的部分结果会通过球体进行可视化直观展示.
把地球搬进实验室?
其核心软件模拟大气圈、水圈、冰冻圈、岩石圈、生物圈的演变规律,对地球的过去进行反演、对现在进行观察、对未来进行预测.
2021年6月23日,国家重大科技基础设施“地球模拟装置”——寰,在北京怀柔科学城东区落成启用,这是我国首个研制成功的地球系统数值模拟大科学装置.
展厅中这个直径3米LED球形屏上风起云涌,颇为壮观.它究竟有多大,占据多大空间?表面积多少呢?
探索新知——球的截面
探究一 球的截面
类比
1.一条直线与圆相交,在圆内的部分是线段——弦?
用一个平面去截球,得到的截面是什么?
圆面
用一个平面去截球面,得到的截面是什么?
圆
什么情况下,得到的圆最大?
2.直线过圆心时,得到的弦最长——直径.
探索新知——球的截面
球的大圆:球面被经过球心的平面截得的圆.
一 大小圆的定义
球的小圆:球面被不经过球心的平面截得的圆.
探索新知——球的截面
探究一 球的截面
类比
垂径定理:垂直于弦的直径平分弦所对的两条弧.
1.圆心与弦中点的连线垂直于弦.
球心与截面圆心的连线与圆面是怎样的位置关系呢?
1.球心与截面圆心的连线与圆面垂直.
探索新知——球的切线
探究二 球的切线
类比
1.直线与圆有唯一公共点时,叫做直线与圆相切.
2.过圆外一点可以引2条直线与圆相切,且切线长相等.
1.球的切线怎样定义?
2.过球外一点P,可以引多少条直线与球相切?
3.这些切线的长度相等吗?所有切点组成什么图形?
探索新知——球的体积和表面积
探究三 球的表面积和体积
(1)球的表面积:能否采用展开的方法,求球体的表面积呢?
(2)球的体积:给你一个半径为R的实心铁球,如何测量该球的体积呢?
思考:当球的半径变化时,球的体积随之改变,你是否每次都要这样测量呢?
不能,球体无法展开为一个平面图形
排水法
H
R
h
延伸阅读——祖暅原理
“幂势既同,则积不容异”
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
课后探究:查阅资料,阿基米德是如何推算出球体体积的?如何推导求球的表面积计算公式?
延伸阅读——祖暅原理
五 球的表面积和体积计算公式
探索新知——球的体积和表面积
O R
思考:计算球的表面积与体积,关键需要确定哪个量?
例题讲解——初步应用
例2 如图,一个圆锥形的空杯子上面放着一个半球形的冰激凌,如果冰激凌融化了,会溢出杯子吗?(假设冰激凌融化前后体积不变)
例题讲解——初步应用
O’
∟
R
例题讲解——巩固提升
变式训练2 如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为 .
∟
O
O’
A
例题讲解——巩固提升
过点O作OO’ 该截面交于点O’,
OA=R,故(R-2)2+42=R2,解得R=5 cm.
分析:设球半径为R,正方体容器上底正方形所在平面截球所得截面为圆面,
易知Rt△OO’A中,OO’=R-2,O’A=4,
数学思想
概念
课堂小结
球的表面积和体积
球的截面性质、切线性质
球的表面积和体积计算公式的应用
了解祖暅原理及其相关证明
数学建模、数形结合思想
类比思想、转化和化归思想
作业布置
选做题:教材第252页复习题六 B组第10题.
必做题:教材第244页练习3,同步练习册.
板书设计
6.3《球的表面积和体积》
相关性质: 公式: 投影区域
例题讲解:
谢 谢!
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
