人教版五年级数学下册 最小公倍数 课件(共45张PPT)
文档属性
| 名称 | 人教版五年级数学下册 最小公倍数 课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-18 21:36:48 | ||
图片预览








文档简介
(共45张PPT)
最小公倍数
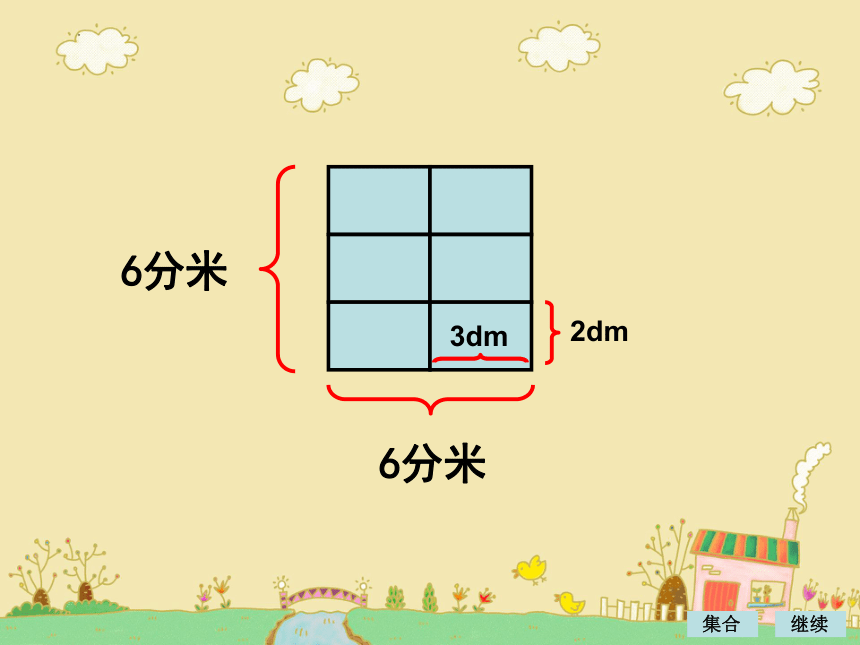
这种墙砖长 3 dm,
宽 2 dm。
1
如果用这种墙砖铺一个正方形(用的墙砖都是整块),正方形的边长可以是多少分米?
最小是多少分米?
6分米
继续
集合
6分米
2dm
3dm
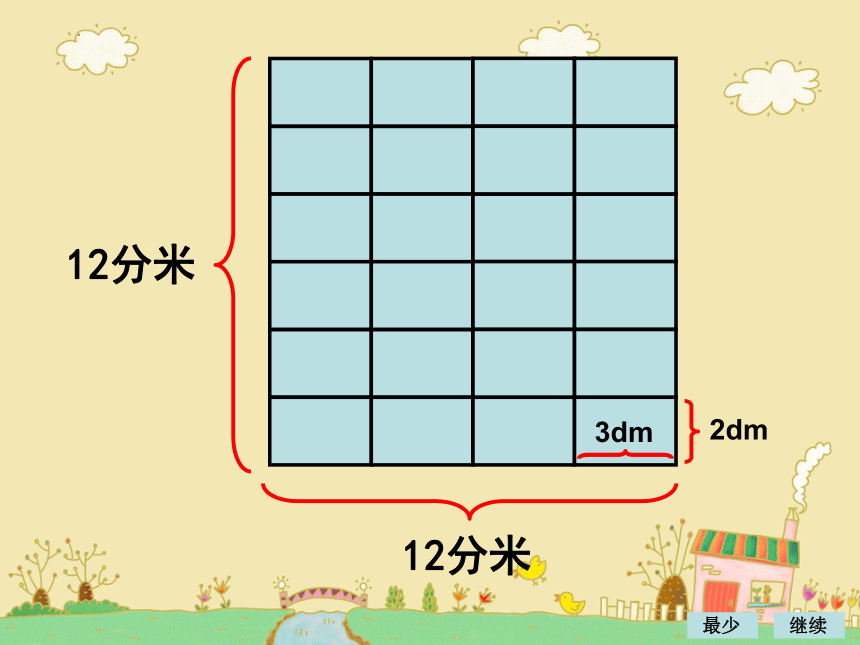
12分米
继续
最少
12分米
3dm
2dm
要铺成正方形,正方形的边长必须
既是3的倍数,又是2的倍数。
3 的倍数
2 的倍数
2, 4, 6, 8, 10, 12, 14, 16, 18, ···
3,6,9,12,15,18,···
这个正方形的边长必须既是 3 的倍数,又是 2 的倍数。
可以铺出边长是 6 dm,12 dm,18 dm,···
的正方形,最小的正方形边长是 6 dm。
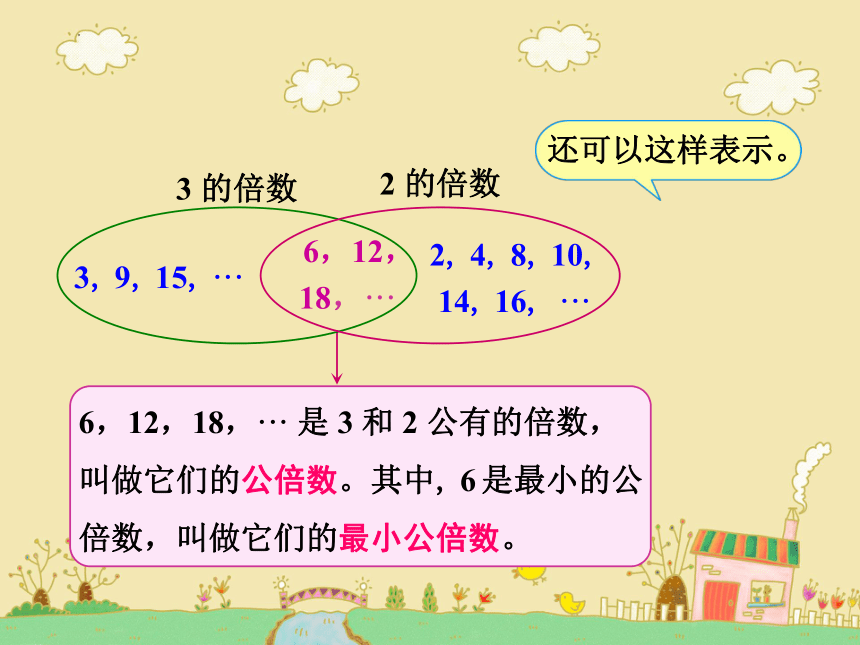
2, 4, 8, 10,
14, 16, ···
3, 9, 15, ···
6,12,18,··· 是 3 和 2 公有的倍数,叫做它们的公倍数。其中, 6 是最小的公倍数,叫做它们的最小公倍数。
3 的倍数
2 的倍数
6,12,
18,···
还可以这样表示。
如果这些学生的总人数在 40 人以内,可能是多少人
咱们可以分成 4 人一组,也可以分成 6 人一组,都正好分完。
40以内:
4的倍数有:4、8、12、16、20、24、28、32、36
6的倍数有:6、12、18、24、30、36
4和6的公倍数有:12、24、36
所以,学生的总人数可能是12人、24人、36人。
怎样求 6 和 8 的最小公倍数
2
6 和 8 的公倍数有很多呢。
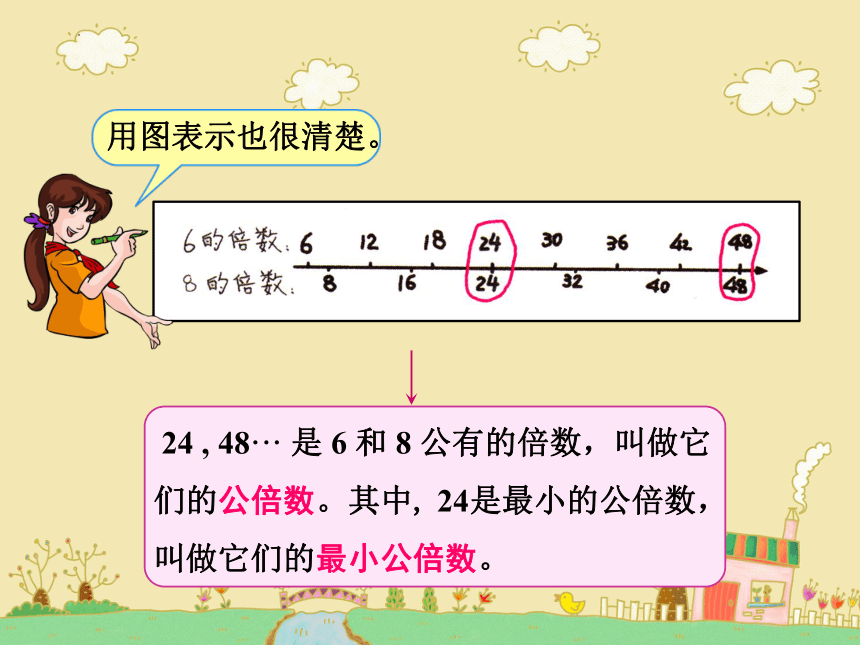
用图表示也很清楚。
24 , 48··· 是 6 和 8 公有的倍数,叫做它们的公倍数。其中, 24是最小的公倍数,叫做它们的最小公倍数。
你还有其他方法吗 和同学讨论一下。
观察一下,两个数的公倍数和它们的最小公倍数之间有什么关系
6 的倍数中有哪些
是 8 的倍数呢
2
3 4
2×3×4=24
6和8的最小公倍数是:24
短除法:
6 8
练一练
1、用短除法求下面每组数的最小公倍数。
6和18
21和14
12和8
公倍数
18
公倍数
42
公倍数
24
找出下列每组数的最小公倍数。你发现了什么
3 和 6
2 和 8
5 和 6
4 和 9
3 和 6 的最小公倍数是 6;
2 和 8 的最小公倍数是 8 ;
5 和 6 的最小公倍数是 30 ;
4 和 9 的最小公倍数是 36。
当两个数是倍数关系时,这两个数的最小公倍数就是较大的数;当两个数是互质数时,这两个数的最小公倍数就是这两个数的积。
发现
说说下列每组数的最小公倍数。
6 和 12 的最小公倍数
9 和 18 的最小公倍数
5 和 10 的最小公倍数
12 和 24 的最小公倍数
2 和 5 的最小公倍数
7 和 9 的最小公倍数
9 和 10 的最小公倍数
19 和 20 的最小公倍数
1. 下面每组数的公倍数中有没有 36 有没有48 有
没有 84
6 和 18 21 和 14 12 和 8
2. 按照从小到大的顺序,从 100 以内的数中找出 6 的倍数和 10 的倍数,再找出它们的公倍数和最小公倍数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3. 求下列每组数的最小公倍数。
2 和 8 3 和 8 6 和 15 6 和 9
4 和 5 1 和 7 4 和 10 8 和 10
8
24
30
18
20
7
20
40
4. 李阿姨今天给月季和君子兰同时浇了水,至少多少
天以后给这两种花同时浇水
月季每 4 天浇一次水,君
子兰每 6 天浇一次水。
4 和 6 的最小公倍数是 12。
答: 至少要 12 天以后给这两种花同时浇水。
5. 下面的说法对吗 说一说你的理由。
(1)两个数的最小公倍数一定比这两个数都大。
错。两个数的最小公倍数不一定比这两个数
都大。比如: 2 和 8 的最小公倍数是 8。
(2)两个数的积一定是这两个数的公倍数。
对。
6.
这块正方形布料,既可以都做成边长是 8 cm 的方巾,也可以都做成边长是 10 cm 的方巾,都没有剩余。
这块正方形布料的边长至少
是多少厘米
8 和 10 的最小公倍数是 40。
答: 这块正方形布料的边长至少是 40 cm。
这两路公共汽车同时发车以后,至少过多少分钟两路车才第二次同时出发
7.
它们刚才同
时发的车。
3 路: 每隔 6 分钟发一次车
5 路: 每隔 8 分钟发一次车
3 路和 5 路的起
点站都在这儿。
6 和 8 的最小公倍数是 24,
所以至少过 24 分钟两路车才第二次同时发车。
(1)如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇 此时爸爸、妈妈分别跑了多少圈
8.
我跑一圈用
3 分钟。
我跑一圈用 4 分钟。
我要用
6 分钟。
4 和 3 的最小公倍数是 12。
所以爸爸、妈妈至少 12 分钟后两人在起点再次相遇。
12÷3 = 4(圈)
12÷4 = 3(圈)
答: 此时爸爸跑了 4 圈,妈妈跑了 3 圈。
(2)你还能提出什么问题
9.* 36 可能是哪两个数的最小公倍数 你能找出
几组
我们也可以利用分解质因数的方法,比较简便
地求出两个数的最小公倍数。
例如:
60 = 2×2×3×5
42 = 2×3×7
60 和 42 的最小公倍数 = 2×3×2×5×7 = 420。
两个数的最小公倍数等于两个数的所有公有质因数和独有质因数的乘积
【例1】五年级同学参加植树劳动,按照15人一组 或者18人一组,都正好分完,问:参加植树劳动的五年级同学至少有多少人
解:
题意就是要求15和18的最小公倍数。
答:参加植物劳动的五年级同学有90人。
【例2】人民公园是1路和6路汽车的起点站。1路汽车每3分钟发车一次,6路汽车每5分钟发车一 次。这两路汽车同时发车以后,至少再过多久又同时发车?
1路
6路
解:
题意就是要求3和5的最小公倍数。
3× 5 = 15
答:至少再过15分钟又同时发车。
用短除法求下面每组数的最大公倍数
30和45
24和36
30 45
5
6
9
3
2
3
30和45的最大公约数是5 × 3=15。
36 24
18
12
2
9
6
3
3
2
36和24的最大公约数是
2 × 2 × 3=12。
复习
2
复习
把6和15的倍数和公倍数填在下面的圈内,再找出它们的最小公倍数。
6的倍数
15的倍数
6的倍数
15的倍数
6和15的公倍数
6、12、18、24、30、36、42、48、54、60、…
15、30、45、 60、75、…
30、60、…
6、12、18、24、…
15、45、75、…
几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
小结
例2 求12和30的最小公倍数。
12的倍数:
30的倍数:
12、24、36、48、60、72、…
30、60、90、…
60
60
12和30的最小公倍数是60。
例题
2 × 3 × 2
2 × 3 × 5
12=
30=
12和30的最小公倍数是
2×3×2×5=60
公有的质因数与各自独有的质因数连乘的积就是它们的最小公倍数。
求12和30的最小公倍数
例题
求42和70的最小公倍数
42=2×3×7
70=2×5×7
42和70的最小公倍数是
2×7×3×5=210
练习
例3 求36和45的最小公倍数。
3
3
36
45
12
15
4
5
36和45的最小公倍数是3×3×4×5=180
所有的除数与最后的商连乘的积就是两个数的最小公倍数。
例题
求30和40最小公倍数
2
5
30
40
15
20
3
4
30和40的最小公倍数是2×5×3×4=120
练习
求下面每组数的最小公倍数。
20和40
26和13
8 和 1
20和40的最小公倍数是40
26和13的最小公倍数是26
8和1的最小公倍数是8
如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
讨论
求下面每组数的最小公倍数。
8和9
2和11
7 和 4
8和9的最小公倍数是8×9=72
7和4的最小公倍数是7×4=28
2和11的最小公倍数是2×11=22
如果两个数是互质数,那么这两个数的乘积就是它们的最小公倍数。
讨论
求两个数的最小公倍数的方法
分解法:公有的质因数与各自独有的质因数连乘的积就是它们的最小公倍数。
短除法:所有的除数与最后的商连乘的积就是两个数的最小公倍数。
如果较大数是较小数的倍数,那
么较大数就是这两个数的最小公倍数。
如果两个数是互质数,那么这两个数的乘积就是它们的最小公倍数。
小结
判断题
(1) 12 和 18
2
6
12
18
9
12和18的最小公倍数是2×6×9=108
( )
×
(2) A=12,B=5,A和B的最小公倍数是12×5=60
( )
√
练习
(3)
2
2
16
12
8
6
4
3
16和12的最小公倍数是2×4×3=24
( )
×
(4)甲=36,乙=18,甲乙两数的最小公倍数是18
( )
×
练习
选择题
(1)甲数=2×2×3,乙数=2×3×3,甲乙两数的最小公倍数是( )。
A、2×3
B、3×3
C、2×2×3×3
D、2×2×3×3×3
C
(2)6和9的最小公倍数是( )。
A、6 B、9
C、54 D、18
D
练习
填空
(1)A=2×3×5,B=3×3×5,A、B两数的最大公约数是( ),最小公倍数是( )。
15
90
(2)如果M÷N=5,M、N都是自然数,那么M和N的最大公约数是( ),最小公倍数是( )。
N
M
练习
1:两数既不互质,又不是倍数,除了用短除法去求,还有其它方法吗?
2:求两个数的最大公约数和最小公倍数有什么相同点和不同点
思考
最小公倍数
这种墙砖长 3 dm,
宽 2 dm。
1
如果用这种墙砖铺一个正方形(用的墙砖都是整块),正方形的边长可以是多少分米?
最小是多少分米?
6分米
继续
集合
6分米
2dm
3dm
12分米
继续
最少
12分米
3dm
2dm
要铺成正方形,正方形的边长必须
既是3的倍数,又是2的倍数。
3 的倍数
2 的倍数
2, 4, 6, 8, 10, 12, 14, 16, 18, ···
3,6,9,12,15,18,···
这个正方形的边长必须既是 3 的倍数,又是 2 的倍数。
可以铺出边长是 6 dm,12 dm,18 dm,···
的正方形,最小的正方形边长是 6 dm。
2, 4, 8, 10,
14, 16, ···
3, 9, 15, ···
6,12,18,··· 是 3 和 2 公有的倍数,叫做它们的公倍数。其中, 6 是最小的公倍数,叫做它们的最小公倍数。
3 的倍数
2 的倍数
6,12,
18,···
还可以这样表示。
如果这些学生的总人数在 40 人以内,可能是多少人
咱们可以分成 4 人一组,也可以分成 6 人一组,都正好分完。
40以内:
4的倍数有:4、8、12、16、20、24、28、32、36
6的倍数有:6、12、18、24、30、36
4和6的公倍数有:12、24、36
所以,学生的总人数可能是12人、24人、36人。
怎样求 6 和 8 的最小公倍数
2
6 和 8 的公倍数有很多呢。
用图表示也很清楚。
24 , 48··· 是 6 和 8 公有的倍数,叫做它们的公倍数。其中, 24是最小的公倍数,叫做它们的最小公倍数。
你还有其他方法吗 和同学讨论一下。
观察一下,两个数的公倍数和它们的最小公倍数之间有什么关系
6 的倍数中有哪些
是 8 的倍数呢
2
3 4
2×3×4=24
6和8的最小公倍数是:24
短除法:
6 8
练一练
1、用短除法求下面每组数的最小公倍数。
6和18
21和14
12和8
公倍数
18
公倍数
42
公倍数
24
找出下列每组数的最小公倍数。你发现了什么
3 和 6
2 和 8
5 和 6
4 和 9
3 和 6 的最小公倍数是 6;
2 和 8 的最小公倍数是 8 ;
5 和 6 的最小公倍数是 30 ;
4 和 9 的最小公倍数是 36。
当两个数是倍数关系时,这两个数的最小公倍数就是较大的数;当两个数是互质数时,这两个数的最小公倍数就是这两个数的积。
发现
说说下列每组数的最小公倍数。
6 和 12 的最小公倍数
9 和 18 的最小公倍数
5 和 10 的最小公倍数
12 和 24 的最小公倍数
2 和 5 的最小公倍数
7 和 9 的最小公倍数
9 和 10 的最小公倍数
19 和 20 的最小公倍数
1. 下面每组数的公倍数中有没有 36 有没有48 有
没有 84
6 和 18 21 和 14 12 和 8
2. 按照从小到大的顺序,从 100 以内的数中找出 6 的倍数和 10 的倍数,再找出它们的公倍数和最小公倍数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
3. 求下列每组数的最小公倍数。
2 和 8 3 和 8 6 和 15 6 和 9
4 和 5 1 和 7 4 和 10 8 和 10
8
24
30
18
20
7
20
40
4. 李阿姨今天给月季和君子兰同时浇了水,至少多少
天以后给这两种花同时浇水
月季每 4 天浇一次水,君
子兰每 6 天浇一次水。
4 和 6 的最小公倍数是 12。
答: 至少要 12 天以后给这两种花同时浇水。
5. 下面的说法对吗 说一说你的理由。
(1)两个数的最小公倍数一定比这两个数都大。
错。两个数的最小公倍数不一定比这两个数
都大。比如: 2 和 8 的最小公倍数是 8。
(2)两个数的积一定是这两个数的公倍数。
对。
6.
这块正方形布料,既可以都做成边长是 8 cm 的方巾,也可以都做成边长是 10 cm 的方巾,都没有剩余。
这块正方形布料的边长至少
是多少厘米
8 和 10 的最小公倍数是 40。
答: 这块正方形布料的边长至少是 40 cm。
这两路公共汽车同时发车以后,至少过多少分钟两路车才第二次同时出发
7.
它们刚才同
时发的车。
3 路: 每隔 6 分钟发一次车
5 路: 每隔 8 分钟发一次车
3 路和 5 路的起
点站都在这儿。
6 和 8 的最小公倍数是 24,
所以至少过 24 分钟两路车才第二次同时发车。
(1)如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇 此时爸爸、妈妈分别跑了多少圈
8.
我跑一圈用
3 分钟。
我跑一圈用 4 分钟。
我要用
6 分钟。
4 和 3 的最小公倍数是 12。
所以爸爸、妈妈至少 12 分钟后两人在起点再次相遇。
12÷3 = 4(圈)
12÷4 = 3(圈)
答: 此时爸爸跑了 4 圈,妈妈跑了 3 圈。
(2)你还能提出什么问题
9.* 36 可能是哪两个数的最小公倍数 你能找出
几组
我们也可以利用分解质因数的方法,比较简便
地求出两个数的最小公倍数。
例如:
60 = 2×2×3×5
42 = 2×3×7
60 和 42 的最小公倍数 = 2×3×2×5×7 = 420。
两个数的最小公倍数等于两个数的所有公有质因数和独有质因数的乘积
【例1】五年级同学参加植树劳动,按照15人一组 或者18人一组,都正好分完,问:参加植树劳动的五年级同学至少有多少人
解:
题意就是要求15和18的最小公倍数。
答:参加植物劳动的五年级同学有90人。
【例2】人民公园是1路和6路汽车的起点站。1路汽车每3分钟发车一次,6路汽车每5分钟发车一 次。这两路汽车同时发车以后,至少再过多久又同时发车?
1路
6路
解:
题意就是要求3和5的最小公倍数。
3× 5 = 15
答:至少再过15分钟又同时发车。
用短除法求下面每组数的最大公倍数
30和45
24和36
30 45
5
6
9
3
2
3
30和45的最大公约数是5 × 3=15。
36 24
18
12
2
9
6
3
3
2
36和24的最大公约数是
2 × 2 × 3=12。
复习
2
复习
把6和15的倍数和公倍数填在下面的圈内,再找出它们的最小公倍数。
6的倍数
15的倍数
6的倍数
15的倍数
6和15的公倍数
6、12、18、24、30、36、42、48、54、60、…
15、30、45、 60、75、…
30、60、…
6、12、18、24、…
15、45、75、…
几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
小结
例2 求12和30的最小公倍数。
12的倍数:
30的倍数:
12、24、36、48、60、72、…
30、60、90、…
60
60
12和30的最小公倍数是60。
例题
2 × 3 × 2
2 × 3 × 5
12=
30=
12和30的最小公倍数是
2×3×2×5=60
公有的质因数与各自独有的质因数连乘的积就是它们的最小公倍数。
求12和30的最小公倍数
例题
求42和70的最小公倍数
42=2×3×7
70=2×5×7
42和70的最小公倍数是
2×7×3×5=210
练习
例3 求36和45的最小公倍数。
3
3
36
45
12
15
4
5
36和45的最小公倍数是3×3×4×5=180
所有的除数与最后的商连乘的积就是两个数的最小公倍数。
例题
求30和40最小公倍数
2
5
30
40
15
20
3
4
30和40的最小公倍数是2×5×3×4=120
练习
求下面每组数的最小公倍数。
20和40
26和13
8 和 1
20和40的最小公倍数是40
26和13的最小公倍数是26
8和1的最小公倍数是8
如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
讨论
求下面每组数的最小公倍数。
8和9
2和11
7 和 4
8和9的最小公倍数是8×9=72
7和4的最小公倍数是7×4=28
2和11的最小公倍数是2×11=22
如果两个数是互质数,那么这两个数的乘积就是它们的最小公倍数。
讨论
求两个数的最小公倍数的方法
分解法:公有的质因数与各自独有的质因数连乘的积就是它们的最小公倍数。
短除法:所有的除数与最后的商连乘的积就是两个数的最小公倍数。
如果较大数是较小数的倍数,那
么较大数就是这两个数的最小公倍数。
如果两个数是互质数,那么这两个数的乘积就是它们的最小公倍数。
小结
判断题
(1) 12 和 18
2
6
12
18
9
12和18的最小公倍数是2×6×9=108
( )
×
(2) A=12,B=5,A和B的最小公倍数是12×5=60
( )
√
练习
(3)
2
2
16
12
8
6
4
3
16和12的最小公倍数是2×4×3=24
( )
×
(4)甲=36,乙=18,甲乙两数的最小公倍数是18
( )
×
练习
选择题
(1)甲数=2×2×3,乙数=2×3×3,甲乙两数的最小公倍数是( )。
A、2×3
B、3×3
C、2×2×3×3
D、2×2×3×3×3
C
(2)6和9的最小公倍数是( )。
A、6 B、9
C、54 D、18
D
练习
填空
(1)A=2×3×5,B=3×3×5,A、B两数的最大公约数是( ),最小公倍数是( )。
15
90
(2)如果M÷N=5,M、N都是自然数,那么M和N的最大公约数是( ),最小公倍数是( )。
N
M
练习
1:两数既不互质,又不是倍数,除了用短除法去求,还有其它方法吗?
2:求两个数的最大公约数和最小公倍数有什么相同点和不同点
思考
