人教版九年级数学上册24.1.2垂径定理
文档属性
| 名称 | 人教版九年级数学上册24.1.2垂径定理 |  | |
| 格式 | zip | ||
| 文件大小 | 397.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-27 00:11:54 | ||
图片预览





文档简介
课件22张PPT。24.1.2 垂直于弦的直径12学习目标 把一个圆沿着它的任意一条直径对折,
重复几次,你发现了什么?由此你能得到
什么结论?可以发现:
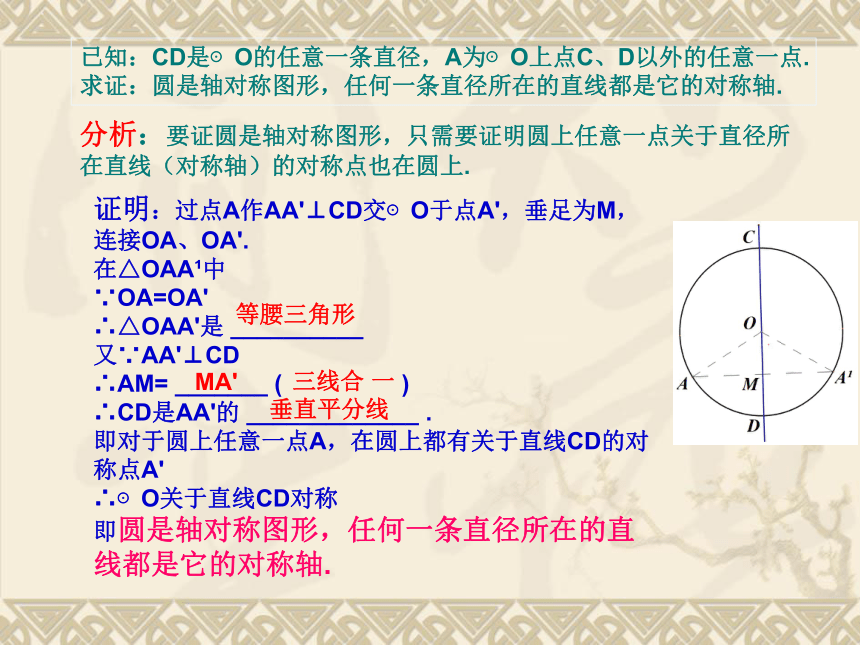
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 活动一已知:CD是⊙O的任意一条直径,A为⊙O上点C、D以外的任意一点.
求证:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴.分析:要证圆是轴对称图形,只需要证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.证明:过点A作AA'⊥CD交⊙O于点A',垂足为M,连接OA、OA'.
在△OAA1中
∵OA=OA'
∴△OAA'是 __________
又∵AA'⊥CD
∴AM= _______ ( )
∴CD是AA'的 _____________ .
即对于圆上任意一点A,在圆上都有关于直线CD的对称点A'
∴⊙O关于直线CD对称
即圆是轴对称图形,任何一条直径所在的直线都是它的对称轴.等腰三角形MA'三线合 一垂直平分线如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB于E点.·OABCDE 你能发现图中有那些相等的线段和弧?为什么?把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC与BC重合,AD与BD重合.因此 AE=BE
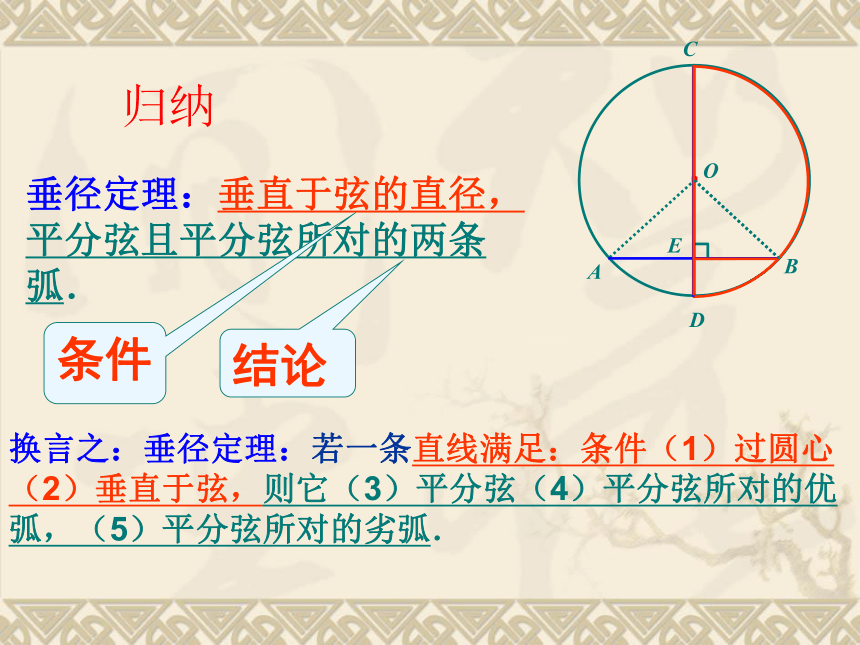
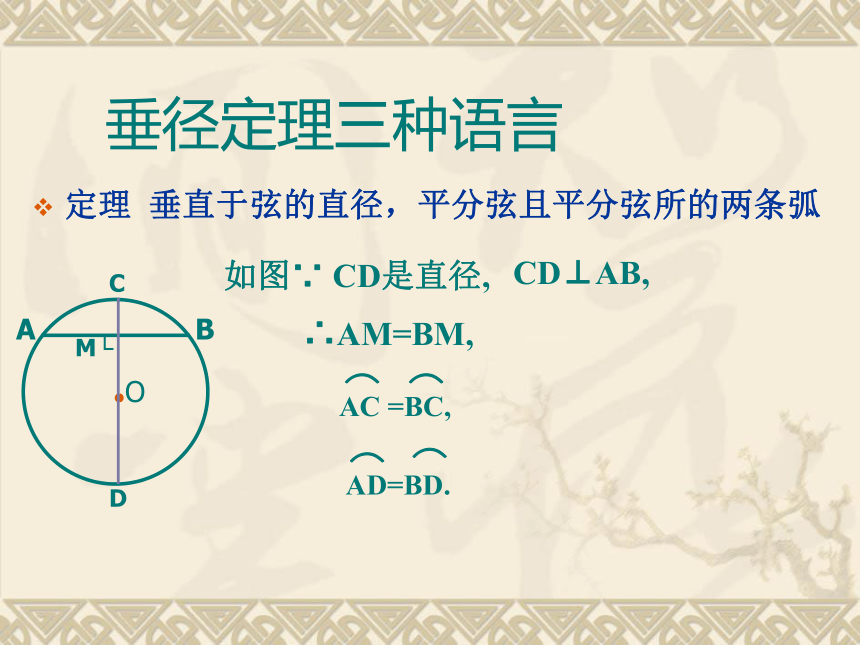
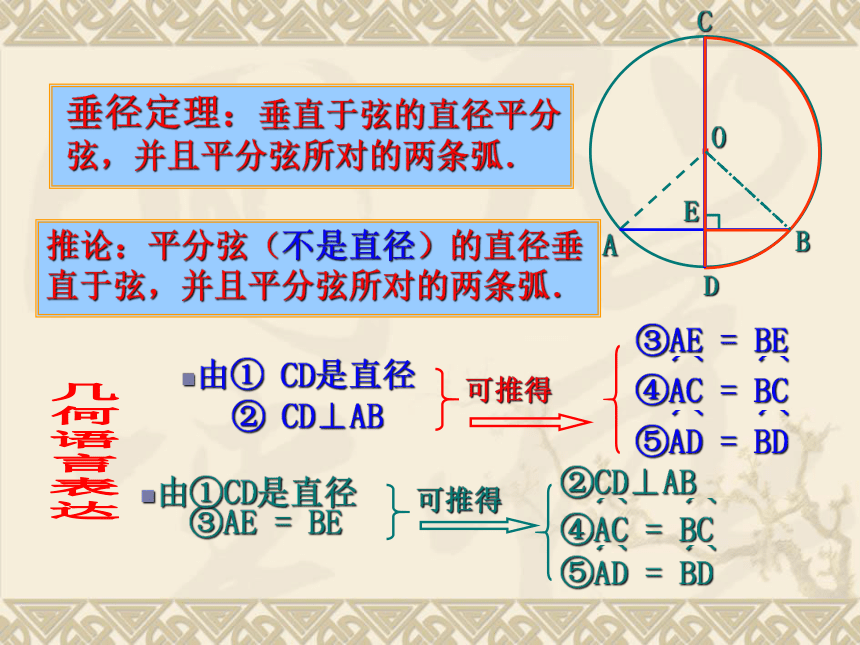
即 直径CD平分弦AB,并且平分AB及ACB⌒⌒AC=BC⌒⌒AD=BD⌒⌒⌒OBCD·AE⌒⌒⌒⌒·OABCDE垂径定理:垂直于弦的直径,平分弦且平分弦所对的两条弧.归纳条件结论换言之:垂径定理:若一条直线满足:条件(1)过圆心(2)垂直于弦,则它(3)平分弦(4)平分弦所对的优弧,(5)平分弦所对的劣弧.垂径定理三种语言定理 垂直于弦的直径,平分弦且平分弦所的两条弧CD⊥AB,如图∵ CD是直径,∴AM=BM,·OABCDE几
何
语
言
表
达下列图形是否具备垂径定理的条件?是不是是火眼金睛不是借你慧眼垂径定理的几个基本图形。CD过圆心CD⊥AB于EAE=BE1. 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。解:连结OA,作OE⊥AB于点E,
则OE=3厘米,AE=BE.
∵AB=8厘米
∴AE=4厘米
在RtAOE中,据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。 练习 2. 如图,AB是⊙O的一条弦, CD是直径,且AE=BE
OE=6,AB=16,求⊙O的半径·OABCDE练一练:例题 :你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 37m7.23mABOCD解得:R≈27.3(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.52+(R-7.23)2∴赵州桥的主桥拱半径约为27.3m.OA2 = AD2 + OD2OD = OC-CD = R-7.23在图中 AB=37,CD=7.23,3.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形.提高练习 4.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
∴ AE-CE=BE-DE
即 AC=BD注意:解决有关弦的问题,常过圆心作弦的弦心距,或作垂直于弦的直径,它是一种常用辅助线的添法.总结: 解决有关弦的问题,经常是过圆心作弦的弦心距,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。归纳小结 1、圆是 _____图形,_____________ 所在的直线都是它的对称轴.
2、垂径定理:_______________平分弦,并且平分弦__________ .
推论:平分弦(不是 _____)的直径 _______弦,并且_______弦所对的两条弧.
3、学习反思:_______________________
_______________________
.轴对称任何一条直径垂直于弦的直径所对的两弧直径垂直于平分Thank you!谢谢同学们的努力!
重复几次,你发现了什么?由此你能得到
什么结论?可以发现:
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 活动一已知:CD是⊙O的任意一条直径,A为⊙O上点C、D以外的任意一点.
求证:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴.分析:要证圆是轴对称图形,只需要证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.证明:过点A作AA'⊥CD交⊙O于点A',垂足为M,连接OA、OA'.
在△OAA1中
∵OA=OA'
∴△OAA'是 __________
又∵AA'⊥CD
∴AM= _______ ( )
∴CD是AA'的 _____________ .
即对于圆上任意一点A,在圆上都有关于直线CD的对称点A'
∴⊙O关于直线CD对称
即圆是轴对称图形,任何一条直径所在的直线都是它的对称轴.等腰三角形MA'三线合 一垂直平分线如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB于E点.·OABCDE 你能发现图中有那些相等的线段和弧?为什么?把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC与BC重合,AD与BD重合.因此 AE=BE
即 直径CD平分弦AB,并且平分AB及ACB⌒⌒AC=BC⌒⌒AD=BD⌒⌒⌒OBCD·AE⌒⌒⌒⌒·OABCDE垂径定理:垂直于弦的直径,平分弦且平分弦所对的两条弧.归纳条件结论换言之:垂径定理:若一条直线满足:条件(1)过圆心(2)垂直于弦,则它(3)平分弦(4)平分弦所对的优弧,(5)平分弦所对的劣弧.垂径定理三种语言定理 垂直于弦的直径,平分弦且平分弦所的两条弧CD⊥AB,如图∵ CD是直径,∴AM=BM,·OABCDE几
何
语
言
表
达下列图形是否具备垂径定理的条件?是不是是火眼金睛不是借你慧眼垂径定理的几个基本图形。CD过圆心CD⊥AB于EAE=BE1. 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。解:连结OA,作OE⊥AB于点E,
则OE=3厘米,AE=BE.
∵AB=8厘米
∴AE=4厘米
在RtAOE中,据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。 练习 2. 如图,AB是⊙O的一条弦, CD是直径,且AE=BE
OE=6,AB=16,求⊙O的半径·OABCDE练一练:例题 :你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 37m7.23mABOCD解得:R≈27.3(m)解决求赵州桥拱半径的问题在Rt△OAD中,由勾股定理,得即 R2=18.52+(R-7.23)2∴赵州桥的主桥拱半径约为27.3m.OA2 = AD2 + OD2OD = OC-CD = R-7.23在图中 AB=37,CD=7.23,3.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形.提高练习 4.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
∴ AE-CE=BE-DE
即 AC=BD注意:解决有关弦的问题,常过圆心作弦的弦心距,或作垂直于弦的直径,它是一种常用辅助线的添法.总结: 解决有关弦的问题,经常是过圆心作弦的弦心距,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。归纳小结 1、圆是 _____图形,_____________ 所在的直线都是它的对称轴.
2、垂径定理:_______________平分弦,并且平分弦__________ .
推论:平分弦(不是 _____)的直径 _______弦,并且_______弦所对的两条弧.
3、学习反思:_______________________
_______________________
.轴对称任何一条直径垂直于弦的直径所对的两弧直径垂直于平分Thank you!谢谢同学们的努力!
同课章节目录
