2016届山东省泰安市岱岳区九上数学(青岛版)学案:3.3 圆周角
文档属性
| 名称 | 2016届山东省泰安市岱岳区九上数学(青岛版)学案:3.3 圆周角 |  | |
| 格式 | zip | ||
| 文件大小 | 383.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-27 07:46:34 | ||
图片预览




文档简介
课题 3.3 圆周角(第1课时) 课型 新授
内容 九上教科书81--84页 主备人
学习目标 1. 理解圆周角的概念;2. 能说出圆周角与圆心角及其所对弧的关系,证明圆周角定理及其推论;3.能运用圆周角定理及其推论解决有关问题.
重点 能运用圆周角定理及其推论解决有关问题.
难点 探索圆周角与圆心角及其所对弧的关系,证明圆周角定理及其推论的过程.
学前预习案
独立阅读81--84页的内容,约10分钟,要求:1.知识回顾什么是圆心角? 答:___________________________________________.2. 什么是圆周角? 答:____________________________________________.
课堂学习案
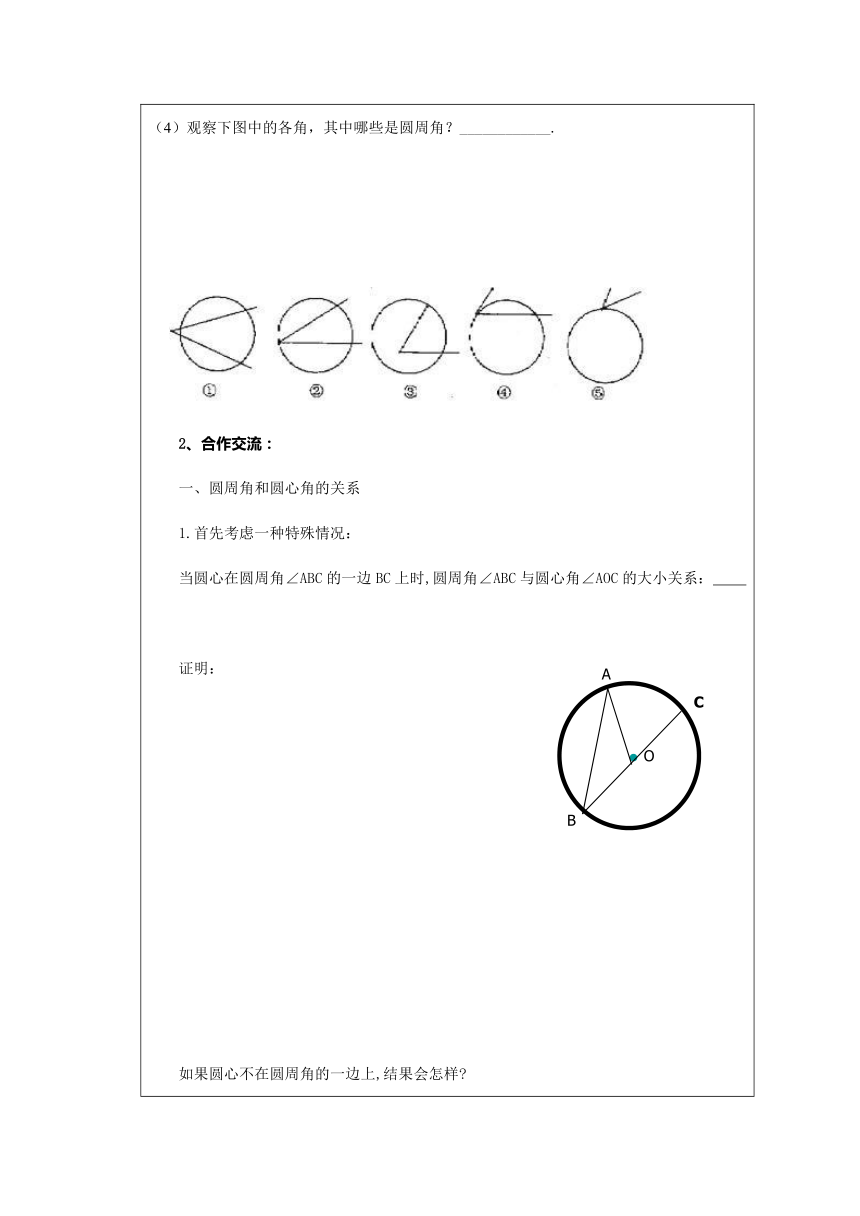
一、合作探究1、自主探究(1).如图,点 A,B,C 是⊙O 上的三个点. 以 C 为端点作射线 CA,CB,得到了一个怎样的角?(2).(1)中的∠ACB 有什么特征?∠ACB 的________在圆上,并且它的两边在圆内的部分是_______________,像这样的角叫做圆周角.(3)圆周角与圆心角有什么不同?(4)观察下图中的各角,其中哪些是圆周角?____________.2、合作交流:一、圆周角和圆心角的关系1.首先考虑一种特殊情况:当圆心在圆周角∠ABC的一边BC上时,圆周角∠ABC与圆心角∠AOC的大小关系: 证明:如果圆心不在圆周角的一边上,结果会怎样 2.当圆心O在圆周角∠ABC的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样 证明:3.当圆心O在圆周角∠ABC的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样 证明:把你的发现写下来:圆周角定理: 总结:定理证明用的是“分类讨论”方法.先证明圆心在圆周角的边上这种特殊情况,再证明圆心在圆周角的内部和圆心在圆周角的外部的情况.对后两种情况,是通过添加辅助线——作过圆周角顶点的直径.转化成已证过的特殊情况加以解决.这种“转化”思想方法是一种重要的数学思想方法.解题时我们总是把复杂问题转化成简单问题,把一般情况转比成特殊情况,把未知问题转化成已知问题.学习圆周角定理,不仅要掌握定理的内容,还要重视对定理证明过程中所使用的“分类讨论”和“转化”方法的理解.在今后的学习中和解决数学问题时,应逐步学会运用这些方法因为圆心角与它所对弧的度数相等,因而由圆周角定理可以直接得到:推论 1 : _______________________________________________________。例1 如图 3-26,在⊙O 中,∠AOB = 110°,点 C 在 AB 上. 求∠ACB 的度数.三、应用练习判断下列各图形中的角是不是圆周角,并说明理由.四、变式训练试找出图中所有相等的圆周角当堂检测 1、下列各图中,是圆周角的是 2、 图3中有几个圆周角?( )(A)2个 (B)3个 (C)4个 (D)5个 ( http: / / www.21cnjy.com )3、 写出图4中的圆周角:_____________________________ .4、如图,在⊙O中,∠ABC=50°,则∠AOC等于( )A、50°; B、80°;C、90°; D、100°5、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30 °,AB=2,则⊙O的半径是 .6、如图,圆心角∠AOB=100°,则∠ACB=__ _。(5) (6) (7)7、半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 .六、小结,作业1、问题:圆周角与圆心角区别与联系?2、作业: 必做题:练习1、2题。
课后拓展案
如图,圆周角∠ACB与∠ADB的关系?圆心角∠AOB是弧AB所对的.∠ACB、 ∠ADB、∠AOB有什么关系?
课题 3.3 圆周角(第2课时) 课型 新授
内容 九上教科书84--87页 主备人
学习目标 1.能说出圆周角定理得推论2与推论3;2.能运用圆周角定理的推论解决有关问题.
重点 推论2与推论3应用。
难点 探索推论2与推论3的过程.
学前预习案
(1)、对于一般的圆周角,又有什么规律呢 ( http: / / www.21cnjy.com )?
(2)、试一试
发现:同弧所对的圆周角的度数相等. 并且圆周角的度数恰好为同弧所对的圆心角的度数的一半.
课堂学习案
所以∠ABC=180°-∠A-∠ACB
= = °.(2)如图,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE、∠DOE的度数.(3)如图24.1-15, ⊙O的直径AB为10cm, 弦AC为6cm, ∠ACB的平分线交⊙O于D,求BC、AD、BD的长.六、小结,作业1、小结2、作业: 必做题:练习1、2
课后拓展案
1、如图 3-31,AB 是⊙O 的直径, ( http: / / www.21cnjy.com )E 为⊙O 上的一点,C 是AE 的中点. CD⊥AB,垂足为点D, AE交CD于点F,连接AC. 求证:AF = CF .
课题 3.3 圆周角(第3课时) 课型 新授
内容 九上教科书84--87页 主备人 邹范城
学习目标 1.能说出圆内接多边形概念; 2.能说出圆周角定理的推论4;3.能运用圆周角定理的推论4解决有关问题.
重点 推论4的应用.
难点 探索推论4的过程.
学前预习案
独立阅读87--88页的内容,约10分钟,要求:1、观察与思考(1)如图 ,四边形 ABCD 的顶点与⊙O 具有怎样的关系?像这样,___________________________叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 在图 3-32 中,四边形 ABCD 是⊙O 的内接四边形,⊙O 是四边形 ABCD 的外接圆.(2)∠A 与∠C 是四边 ( http: / / www.21cnjy.com )形 ABCD 的一组对角,也都是⊙O 的圆周角,它们在⊙O 中所对的分别是哪两条弧?这两条弧有什么关系?从而∠A 与∠C 具有怎样的数量关系?∠B 与∠D 也具有这样的数量关系吗?
课堂学习案
一、合作探究,归纳性质结合预习案回答下例问题: ∵ 弧BCD 与 弧BAD 的度数之和 ( http: / / www.21cnjy.com )为_________________,由圆周角定理可知,∠A +∠C =_________.同理,∠B +∠D =________.于是,得到圆周角定理的第 4 个推论:推论 4 : ___________________________________.二、例题学习学习例4、5.三、应用练习,巩固性质下列关于圆内接四边形叙述正确的有 ①圆内接四边形的任何一个外角都等于 ( http: / / www.21cnjy.com )它的内对角;②圆内接四边形对角相等;③圆内接四边形中不相邻的两个内角互补;④在圆内部的四边形叫圆内接四边形.A.1个 B.2个 C.3个 D.4个2.圆内接四边形ABCD中,,AC与BD交于点E,在下图中全等三角形的对数为 A.2对 B.3对 C.4对 D.5对3.圆内接四边形ABCD中,,则圆的直径为 A.62 B.63 C.65 D.66 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) T2 T4 T54.如图,四边形ABCD为圆内接四边形,AC为BD的垂直平分线,,则 A. B. C. D.5.圆内接四边形ABCD中,BA与CD的延长线交于点P,AC与BD交于点E,则图中相似三角形有 A.5对 B.4对 C.3对 D.2对四、变式训练,提升能力圆内接四边形ABCD中,,则 .当堂检测1.如图,已知圆内接四边形ABCD的边长为,则四边形ABCD面积为 A. B.8 C. D. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) T1 T2 T52.如图,在以BC为直径的半圆上任取一点P,过弧BP的中点A作于D.连接BP交AD于点E,交AC于点F,则 A.1:1 B.1:2 C.2:1 D.以上结论都不对3.直线与与两坐标轴围成的四边形内接于一个圆,则实数 A.-3 B.3 C.-6 D.6二、填空题4.三角形三边长为5,12,13,则它的外接圆圆心到顶点的距离为 .5.如图,AB为半圆O的直径,C、D为半圆上的两点,,则 .六、小结,作业1、小结2、作业: 必做题:练习1、2
课后拓展案
已知:如图所示,平分. (1)求AC和DB的长; (2)求四边形ACBD的面积.
● O
A
B
C
B
O
A
O
B
C
C
A
A
C
B
O
C
A
B
O
C
A
B
O
A
C
B
O
C
A
B
P
C
D
.O
B
A
内容 九上教科书81--84页 主备人
学习目标 1. 理解圆周角的概念;2. 能说出圆周角与圆心角及其所对弧的关系,证明圆周角定理及其推论;3.能运用圆周角定理及其推论解决有关问题.
重点 能运用圆周角定理及其推论解决有关问题.
难点 探索圆周角与圆心角及其所对弧的关系,证明圆周角定理及其推论的过程.
学前预习案
独立阅读81--84页的内容,约10分钟,要求:1.知识回顾什么是圆心角? 答:___________________________________________.2. 什么是圆周角? 答:____________________________________________.
课堂学习案
一、合作探究1、自主探究(1).如图,点 A,B,C 是⊙O 上的三个点. 以 C 为端点作射线 CA,CB,得到了一个怎样的角?(2).(1)中的∠ACB 有什么特征?∠ACB 的________在圆上,并且它的两边在圆内的部分是_______________,像这样的角叫做圆周角.(3)圆周角与圆心角有什么不同?(4)观察下图中的各角,其中哪些是圆周角?____________.2、合作交流:一、圆周角和圆心角的关系1.首先考虑一种特殊情况:当圆心在圆周角∠ABC的一边BC上时,圆周角∠ABC与圆心角∠AOC的大小关系: 证明:如果圆心不在圆周角的一边上,结果会怎样 2.当圆心O在圆周角∠ABC的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样 证明:3.当圆心O在圆周角∠ABC的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样 证明:把你的发现写下来:圆周角定理: 总结:定理证明用的是“分类讨论”方法.先证明圆心在圆周角的边上这种特殊情况,再证明圆心在圆周角的内部和圆心在圆周角的外部的情况.对后两种情况,是通过添加辅助线——作过圆周角顶点的直径.转化成已证过的特殊情况加以解决.这种“转化”思想方法是一种重要的数学思想方法.解题时我们总是把复杂问题转化成简单问题,把一般情况转比成特殊情况,把未知问题转化成已知问题.学习圆周角定理,不仅要掌握定理的内容,还要重视对定理证明过程中所使用的“分类讨论”和“转化”方法的理解.在今后的学习中和解决数学问题时,应逐步学会运用这些方法因为圆心角与它所对弧的度数相等,因而由圆周角定理可以直接得到:推论 1 : _______________________________________________________。例1 如图 3-26,在⊙O 中,∠AOB = 110°,点 C 在 AB 上. 求∠ACB 的度数.三、应用练习判断下列各图形中的角是不是圆周角,并说明理由.四、变式训练试找出图中所有相等的圆周角当堂检测 1、下列各图中,是圆周角的是 2、 图3中有几个圆周角?( )(A)2个 (B)3个 (C)4个 (D)5个 ( http: / / www.21cnjy.com )3、 写出图4中的圆周角:_____________________________ .4、如图,在⊙O中,∠ABC=50°,则∠AOC等于( )A、50°; B、80°;C、90°; D、100°5、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30 °,AB=2,则⊙O的半径是 .6、如图,圆心角∠AOB=100°,则∠ACB=__ _。(5) (6) (7)7、半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 .六、小结,作业1、问题:圆周角与圆心角区别与联系?2、作业: 必做题:练习1、2题。
课后拓展案
如图,圆周角∠ACB与∠ADB的关系?圆心角∠AOB是弧AB所对的.∠ACB、 ∠ADB、∠AOB有什么关系?
课题 3.3 圆周角(第2课时) 课型 新授
内容 九上教科书84--87页 主备人
学习目标 1.能说出圆周角定理得推论2与推论3;2.能运用圆周角定理的推论解决有关问题.
重点 推论2与推论3应用。
难点 探索推论2与推论3的过程.
学前预习案
(1)、对于一般的圆周角,又有什么规律呢 ( http: / / www.21cnjy.com )?
(2)、试一试
发现:同弧所对的圆周角的度数相等. 并且圆周角的度数恰好为同弧所对的圆心角的度数的一半.
课堂学习案
所以∠ABC=180°-∠A-∠ACB
= = °.(2)如图,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE、∠DOE的度数.(3)如图24.1-15, ⊙O的直径AB为10cm, 弦AC为6cm, ∠ACB的平分线交⊙O于D,求BC、AD、BD的长.六、小结,作业1、小结2、作业: 必做题:练习1、2
课后拓展案
1、如图 3-31,AB 是⊙O 的直径, ( http: / / www.21cnjy.com )E 为⊙O 上的一点,C 是AE 的中点. CD⊥AB,垂足为点D, AE交CD于点F,连接AC. 求证:AF = CF .
课题 3.3 圆周角(第3课时) 课型 新授
内容 九上教科书84--87页 主备人 邹范城
学习目标 1.能说出圆内接多边形概念; 2.能说出圆周角定理的推论4;3.能运用圆周角定理的推论4解决有关问题.
重点 推论4的应用.
难点 探索推论4的过程.
学前预习案
独立阅读87--88页的内容,约10分钟,要求:1、观察与思考(1)如图 ,四边形 ABCD 的顶点与⊙O 具有怎样的关系?像这样,___________________________叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 在图 3-32 中,四边形 ABCD 是⊙O 的内接四边形,⊙O 是四边形 ABCD 的外接圆.(2)∠A 与∠C 是四边 ( http: / / www.21cnjy.com )形 ABCD 的一组对角,也都是⊙O 的圆周角,它们在⊙O 中所对的分别是哪两条弧?这两条弧有什么关系?从而∠A 与∠C 具有怎样的数量关系?∠B 与∠D 也具有这样的数量关系吗?
课堂学习案
一、合作探究,归纳性质结合预习案回答下例问题: ∵ 弧BCD 与 弧BAD 的度数之和 ( http: / / www.21cnjy.com )为_________________,由圆周角定理可知,∠A +∠C =_________.同理,∠B +∠D =________.于是,得到圆周角定理的第 4 个推论:推论 4 : ___________________________________.二、例题学习学习例4、5.三、应用练习,巩固性质下列关于圆内接四边形叙述正确的有 ①圆内接四边形的任何一个外角都等于 ( http: / / www.21cnjy.com )它的内对角;②圆内接四边形对角相等;③圆内接四边形中不相邻的两个内角互补;④在圆内部的四边形叫圆内接四边形.A.1个 B.2个 C.3个 D.4个2.圆内接四边形ABCD中,,AC与BD交于点E,在下图中全等三角形的对数为 A.2对 B.3对 C.4对 D.5对3.圆内接四边形ABCD中,,则圆的直径为 A.62 B.63 C.65 D.66 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) T2 T4 T54.如图,四边形ABCD为圆内接四边形,AC为BD的垂直平分线,,则 A. B. C. D.5.圆内接四边形ABCD中,BA与CD的延长线交于点P,AC与BD交于点E,则图中相似三角形有 A.5对 B.4对 C.3对 D.2对四、变式训练,提升能力圆内接四边形ABCD中,,则 .当堂检测1.如图,已知圆内接四边形ABCD的边长为,则四边形ABCD面积为 A. B.8 C. D. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) T1 T2 T52.如图,在以BC为直径的半圆上任取一点P,过弧BP的中点A作于D.连接BP交AD于点E,交AC于点F,则 A.1:1 B.1:2 C.2:1 D.以上结论都不对3.直线与与两坐标轴围成的四边形内接于一个圆,则实数 A.-3 B.3 C.-6 D.6二、填空题4.三角形三边长为5,12,13,则它的外接圆圆心到顶点的距离为 .5.如图,AB为半圆O的直径,C、D为半圆上的两点,,则 .六、小结,作业1、小结2、作业: 必做题:练习1、2
课后拓展案
已知:如图所示,平分. (1)求AC和DB的长; (2)求四边形ACBD的面积.
● O
A
B
C
B
O
A
O
B
C
C
A
A
C
B
O
C
A
B
O
C
A
B
O
A
C
B
O
C
A
B
P
C
D
.O
B
A
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
