人教版三年级下册数学面积——整理与复习 课件(共21张PPT)
文档属性
| 名称 | 人教版三年级下册数学面积——整理与复习 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
长方形正方形专项训练
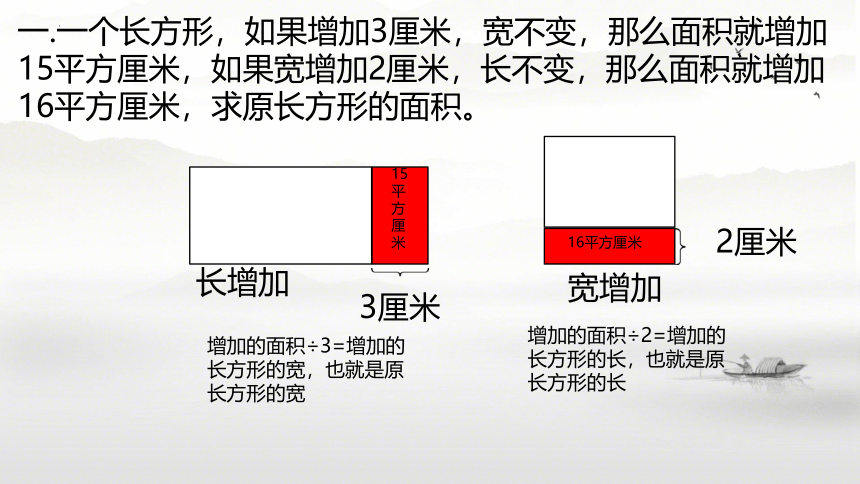
一.一个长方形,如果增加3厘米,宽不变,那么面积就增加15平方厘米,如果宽增加2厘米,长不变,那么面积就增加16平方厘米,求原长方形的面积。
长增加
宽增加
3厘米
2厘米
15平方厘米
16平方厘米
增加的面积÷3=增加的长方形的宽,也就是原长方形的宽
增加的面积÷2=增加的长方形的长,也就是原长方形的长
长增加
宽增加
3厘米
2厘米
15平方厘米
16平方厘米
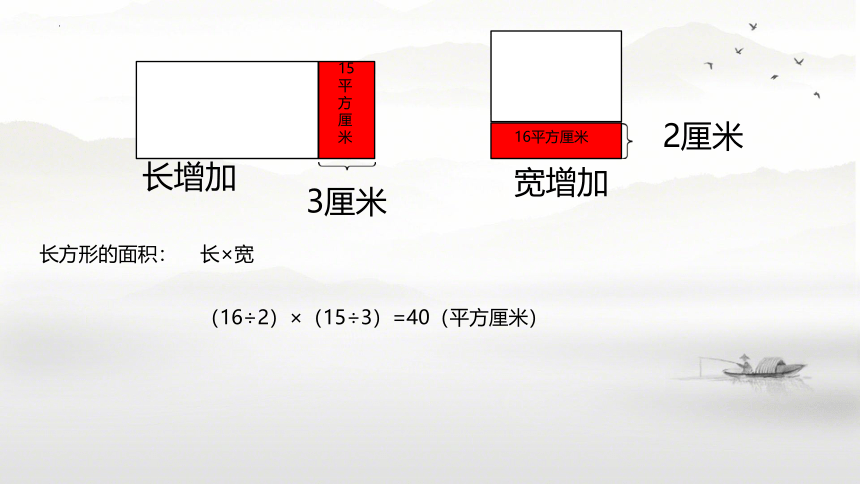
长方形的面积:
长×宽
(16÷2)×(15÷3)=40(平方厘米)
同步仿练:
一个长方形,如果长减少2厘米,宽不变,那么面积就减少10平方厘米这时剩下的部分正好是一个正方形。这个正方形的面积是多少?
减少的面积÷减少的长=原长方形的宽
10÷2=5(厘米)
5×5=25(平方厘米)
二.张老师将两张边长为10厘米的正方形纸板按下面的方式放在了桌子上,重叠部分是边长为3厘米的正方形,桌子被盖住部分的面积是多少?
如果两张纸板没有重叠,那么桌子被盖住部分的面积应该是两张纸板的面积之和,现在有一部分重叠在一起,桌子被盖住部分的面积就少了一个重叠部分的面积。
桌子被盖住部分的面积
=两张纸板的面积之和-重叠部分的面积
10×10×2-3×3=191(平方厘米)
解决此类问题要注意重叠部分的面积
同步仿练:
求阴影部分的面积(单位:厘米)
阴影面积:两个正方形面积之和-中间两个小正方形的面积
9×9+8×8-4×4×2=113(平方厘米)
题目中没有说明重叠!!!
每个大正方形中都有一个小正方形
两个大正方形就有两个小正方形
分割法
求下面图形的面积
不规则图形,可以分割两个规则图形
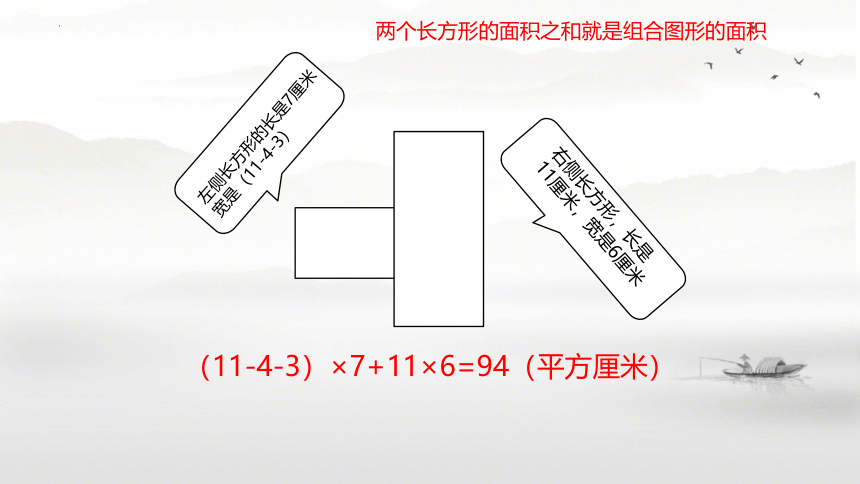
右侧长方形,长是11厘米,宽是6厘米
左侧长方形的长是7厘米
宽是(11-4-3)
两个长方形的面积之和就是组合图形的面积
(11-4-3)×7+11×6=94(平方厘米)
在解决一些不规则图形的面积或组合图形的面积,利用不规则图形的凹凸特点或组合图形的特点,将其分割成若干可以计算的规则图形,先分别求出每个规则图形的面积,再相加求出其总面积。
分割法:
同步仿练:
有一个正方形的花坛,四周有一条1米宽的水泥路,如果水泥路的面积是12平方米,那么花坛的面积是多少?
花坛
12÷4=3(平方米)
3÷1=3(米)
3-1=2(米)
2×2=4(平方米)
花坛
课堂总结
1.由长方形的面积=长×宽可以推出:
长方形的宽=长方形的面积÷长方形的长
长方形的长=长方形的面积÷长方形的宽
2.解决重叠问题要注意重叠部分的面积
3.在解决一些不规则图形的面积或组合图形的面积,利用不规则图形的凹凸特点或组合图形的特点,将其分割成若干可以计算的规则图形,先分别求出每个规则图形的面积,再相加求出其总面积。
一号本作业
1.一个长方形,如果长增加5厘米,宽不变,那么面积就增加40平方厘米,如果宽增加4厘米,长不变,那么面积就增加60平方厘米,求原长方形的面积。
2.一个长方形,如果长减少4分米,宽不变,那么面积就减少16平方分米,如果宽增加3分米,长不变,那么面积就增加18平方分米,求原长方形的面积。
一号本作业
1.一个长方形,如果长增加5厘米,宽不变,那么面积就增加40平方厘米,如果宽增加4厘米,长不变,那么面积就增加60平方厘米,求原长方形的面积。
2.一个长方形,如果长减少4分米,宽不变,那么面积就减少16平方分米,如果宽增加3分米,长不变,那么面积就增加18平方分米,求原长方形的面积。
3.下面重叠部分是边长为2厘米的正方形。计算组合图形的面积()
求下面各图形的面积
如图,在一个大正方形的四个角上各减去一个边长为1厘米的小正方形,剩下的面积是多少?
一号本作业
1.一个长方形,如果长增加5厘米,宽不变,那么面积就增加40平方厘米,如果宽增加4厘米,长不变,那么面积就增加60平方厘米,求原长方形的面积。
2.一个长方形,如果长减少4分米,宽不变,那么面积就减少16平方分米,如果宽增加3分米,长不变,那么面积就增加18平方分米,求原长方形的面积。
(60÷4)×(40÷5)=120(平方厘米)
(18÷3)×(16÷4)=24(平方分米)
3.下面重叠部分是边长为2厘米的正方形。计算组合图形的面积()
9×6+6×4-2×2=74(平方厘米)
求下面各图形的面积
如图,在一个大正方形的四个角上各减去一个边长为1厘米的小正方形,剩下的面积是多少?
4+1+1=6(厘米)
6×6-1×1×4=32(平方厘米)
长方形正方形专项训练
一.一个长方形,如果增加3厘米,宽不变,那么面积就增加15平方厘米,如果宽增加2厘米,长不变,那么面积就增加16平方厘米,求原长方形的面积。
长增加
宽增加
3厘米
2厘米
15平方厘米
16平方厘米
增加的面积÷3=增加的长方形的宽,也就是原长方形的宽
增加的面积÷2=增加的长方形的长,也就是原长方形的长
长增加
宽增加
3厘米
2厘米
15平方厘米
16平方厘米
长方形的面积:
长×宽
(16÷2)×(15÷3)=40(平方厘米)
同步仿练:
一个长方形,如果长减少2厘米,宽不变,那么面积就减少10平方厘米这时剩下的部分正好是一个正方形。这个正方形的面积是多少?
减少的面积÷减少的长=原长方形的宽
10÷2=5(厘米)
5×5=25(平方厘米)
二.张老师将两张边长为10厘米的正方形纸板按下面的方式放在了桌子上,重叠部分是边长为3厘米的正方形,桌子被盖住部分的面积是多少?
如果两张纸板没有重叠,那么桌子被盖住部分的面积应该是两张纸板的面积之和,现在有一部分重叠在一起,桌子被盖住部分的面积就少了一个重叠部分的面积。
桌子被盖住部分的面积
=两张纸板的面积之和-重叠部分的面积
10×10×2-3×3=191(平方厘米)
解决此类问题要注意重叠部分的面积
同步仿练:
求阴影部分的面积(单位:厘米)
阴影面积:两个正方形面积之和-中间两个小正方形的面积
9×9+8×8-4×4×2=113(平方厘米)
题目中没有说明重叠!!!
每个大正方形中都有一个小正方形
两个大正方形就有两个小正方形
分割法
求下面图形的面积
不规则图形,可以分割两个规则图形
右侧长方形,长是11厘米,宽是6厘米
左侧长方形的长是7厘米
宽是(11-4-3)
两个长方形的面积之和就是组合图形的面积
(11-4-3)×7+11×6=94(平方厘米)
在解决一些不规则图形的面积或组合图形的面积,利用不规则图形的凹凸特点或组合图形的特点,将其分割成若干可以计算的规则图形,先分别求出每个规则图形的面积,再相加求出其总面积。
分割法:
同步仿练:
有一个正方形的花坛,四周有一条1米宽的水泥路,如果水泥路的面积是12平方米,那么花坛的面积是多少?
花坛
12÷4=3(平方米)
3÷1=3(米)
3-1=2(米)
2×2=4(平方米)
花坛
课堂总结
1.由长方形的面积=长×宽可以推出:
长方形的宽=长方形的面积÷长方形的长
长方形的长=长方形的面积÷长方形的宽
2.解决重叠问题要注意重叠部分的面积
3.在解决一些不规则图形的面积或组合图形的面积,利用不规则图形的凹凸特点或组合图形的特点,将其分割成若干可以计算的规则图形,先分别求出每个规则图形的面积,再相加求出其总面积。
一号本作业
1.一个长方形,如果长增加5厘米,宽不变,那么面积就增加40平方厘米,如果宽增加4厘米,长不变,那么面积就增加60平方厘米,求原长方形的面积。
2.一个长方形,如果长减少4分米,宽不变,那么面积就减少16平方分米,如果宽增加3分米,长不变,那么面积就增加18平方分米,求原长方形的面积。
一号本作业
1.一个长方形,如果长增加5厘米,宽不变,那么面积就增加40平方厘米,如果宽增加4厘米,长不变,那么面积就增加60平方厘米,求原长方形的面积。
2.一个长方形,如果长减少4分米,宽不变,那么面积就减少16平方分米,如果宽增加3分米,长不变,那么面积就增加18平方分米,求原长方形的面积。
3.下面重叠部分是边长为2厘米的正方形。计算组合图形的面积()
求下面各图形的面积
如图,在一个大正方形的四个角上各减去一个边长为1厘米的小正方形,剩下的面积是多少?
一号本作业
1.一个长方形,如果长增加5厘米,宽不变,那么面积就增加40平方厘米,如果宽增加4厘米,长不变,那么面积就增加60平方厘米,求原长方形的面积。
2.一个长方形,如果长减少4分米,宽不变,那么面积就减少16平方分米,如果宽增加3分米,长不变,那么面积就增加18平方分米,求原长方形的面积。
(60÷4)×(40÷5)=120(平方厘米)
(18÷3)×(16÷4)=24(平方分米)
3.下面重叠部分是边长为2厘米的正方形。计算组合图形的面积()
9×6+6×4-2×2=74(平方厘米)
求下面各图形的面积
如图,在一个大正方形的四个角上各减去一个边长为1厘米的小正方形,剩下的面积是多少?
4+1+1=6(厘米)
6×6-1×1×4=32(平方厘米)
