12.5 因式分解(1)--提公因式法分解因式课件
文档属性
| 名称 | 12.5 因式分解(1)--提公因式法分解因式课件 |  | |
| 格式 | zip | ||
| 文件大小 | 172.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-27 20:46:35 | ||
图片预览








文档简介
课件23张PPT。回忆运用前面所学的知识填空:试一试因式分解(第1课时)12.5 因式分解提公因式法分解因式自探提示:1、什么叫多项式的因式分解?举例说明。
2、因式分解与整式乘法有什么联系和区
别?
3、什么叫公因式?举例说明。
4、因式分解的方法有哪些?什么叫提公因式法?自学课本42页-----43页做一做前的内容并思考把一个多项式化为几个整式的乘积的形式,这就是因式分解.定义如:
1).ma+mb+mc= m?( a+b+c)
2).a2-b2=( a+b)(a-b)
3).a2+2ab+b2=(a+b)2
1).ma+mb+mc= m?( a+b+c)
2).a2-b2=( a+b)(a-b)
3).a2+2ab+b2=(a+b)2
因式分解都是把多项式化为几个整式的积的形式整式乘法都是把整式的积化为多项式的形式因式分解与整式乘法是互逆过程快言快语 抢答判断下列各式哪些是整式乘法?哪些是因式分解?
(1)2x(x-3y) = 2x2-6xy
(2)x2+4x+4 = (x+2)2
(3) m2-4 = (m+2)(m-2)
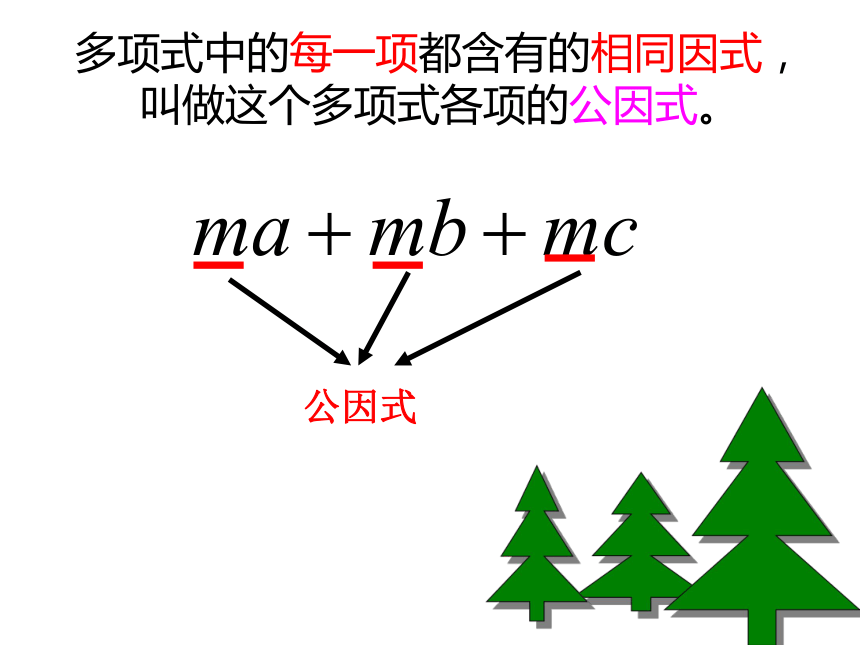
(4)2πR+ 2πr = 2π(R+r)整式乘法因式分解因式分解因式分解多项式中的每一项都含有的相同因式,叫做这个多项式各项的公因式。公因式(1) a c+ b c
(2)3 x2 +9x
(3) a2 b – 2a b2 + ab
(4) 7 ( a– 3 ) – b ( a– 3)
1. 确定下列各多项式中的公因式?c 3xab
a-32. 多项式中的公因式是如何确定的?
(提示:从公因式的系数,字母,字母的指数)我是最棒的!正确找出多项式各项公因式的关键是:定系数公因式的系数是多项式各项系数的最大公因数。(系数是整数时)定字母定指数字母取多项式各项中都含有的相同的字母。
相同字母的指数取各项中最小的一个,即字母最低次幂 例: 找 2x2+ 6x 的公因式。定系数2定字母x 定指数23 如果一个多项式的各项含有公因式,那么
就可以把这个公因式提出来,从而将多项式
化成两个因式乘积的形式,这种分解因式的
方法叫做提公因式法。ma+mb+mc=m( a+b+c )
提公因式法例因式分解的方法有:
1、提公因式法 2、 公式法 把 3a2-9ab因式分解.例1解:原式=3a?a-3a?3b
=3a(a-3b) 注意:⑴提取公因式后,另一个因式不能再含有公因式;⑵另一个因式的项数与原多项式的项数一致。(2)把 -24x3 –12x2 +28x 因式分解.当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
解:原式==1、下列从左到右的变形是分解因式的有( )A. 6x2y=3xy·2x
B. a2-b2+1=(a+b)(a-b)+1
C. a2-ab=a(a-b)
D. (x+3)(x-3)= x2-9
C运用拓展2.若多项式-6ab+18abx+24aby的一个因式是
-6ab,那么另一 个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4yD3.若多项式(a+b)x2+(a+b)x要分解因式,则要提的公因式是 .
(a+b)x4、小明解的有误吗?
当多项式的某一项和公因式相同时,提公因式后剩余的项是1。错误解:抢答我最行!把下列多项式分解因式3a+3b=
5x-5y+5z=
-5a2+25a=
3a2-9ab=3(a+b)5(x-y+z)-5a(a-5)3a(a-3b)?
?
③
把下列各式因式分解:看你能否过关?
a课堂小结:
1、同学们!把你的收获给大家分享 一下!
2、请学科班长评价一下本节课的学习情况!2、确定公因式的方法:
(1)定系数 (2)定字母 (3)定指数小结3、提公因式法因式分解步骤(分两步):
第一步,找出公因式;
第二步,提公因式( 把多项式化为两个因式的乘积)1、什么叫因式分解?4、用提公因式法因式分解应注意的问题:(1)公因式要提尽;
(2)小心漏掉;(3)多项式的首项取正号;(4)公因式是多项式时,要注意符号问题。(1)3.8×0.125+86.2×1/8(2)已知a+b=5,ab=3,求a2b+ab2的值.作业:解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100 =12.5 结果是:15把下列各式分解因式:
1.2a-4b; 2.ax2+ax-4a;
3.3ab2-3a2b; 4.2x3+2x2-6x;
5.7x2+7x+14; 6.-12a2b+24ab2;
7.xy-x2y2-x3y3; 8.27x3+9x2y.练一练拓展题 2、把下列各式因式分解: (1)2m(x+y)+n(x+y);
(2)a(p-q)-4b(q-p);
(3)4a(x-y)2-2b(y-x)2;
(4)2(a-3)2-a+3.
整体思想是数学中一种重要而且常用的思想方法. 公因式既可以是一个单项式的形式,也可以是一个多项式的形式.
2、因式分解与整式乘法有什么联系和区
别?
3、什么叫公因式?举例说明。
4、因式分解的方法有哪些?什么叫提公因式法?自学课本42页-----43页做一做前的内容并思考把一个多项式化为几个整式的乘积的形式,这就是因式分解.定义如:
1).ma+mb+mc= m?( a+b+c)
2).a2-b2=( a+b)(a-b)
3).a2+2ab+b2=(a+b)2
1).ma+mb+mc= m?( a+b+c)
2).a2-b2=( a+b)(a-b)
3).a2+2ab+b2=(a+b)2
因式分解都是把多项式化为几个整式的积的形式整式乘法都是把整式的积化为多项式的形式因式分解与整式乘法是互逆过程快言快语 抢答判断下列各式哪些是整式乘法?哪些是因式分解?
(1)2x(x-3y) = 2x2-6xy
(2)x2+4x+4 = (x+2)2
(3) m2-4 = (m+2)(m-2)
(4)2πR+ 2πr = 2π(R+r)整式乘法因式分解因式分解因式分解多项式中的每一项都含有的相同因式,叫做这个多项式各项的公因式。公因式(1) a c+ b c
(2)3 x2 +9x
(3) a2 b – 2a b2 + ab
(4) 7 ( a– 3 ) – b ( a– 3)
1. 确定下列各多项式中的公因式?c 3xab
a-32. 多项式中的公因式是如何确定的?
(提示:从公因式的系数,字母,字母的指数)我是最棒的!正确找出多项式各项公因式的关键是:定系数公因式的系数是多项式各项系数的最大公因数。(系数是整数时)定字母定指数字母取多项式各项中都含有的相同的字母。
相同字母的指数取各项中最小的一个,即字母最低次幂 例: 找 2x2+ 6x 的公因式。定系数2定字母x 定指数23 如果一个多项式的各项含有公因式,那么
就可以把这个公因式提出来,从而将多项式
化成两个因式乘积的形式,这种分解因式的
方法叫做提公因式法。ma+mb+mc=m( a+b+c )
提公因式法例因式分解的方法有:
1、提公因式法 2、 公式法 把 3a2-9ab因式分解.例1解:原式=3a?a-3a?3b
=3a(a-3b) 注意:⑴提取公因式后,另一个因式不能再含有公因式;⑵另一个因式的项数与原多项式的项数一致。(2)把 -24x3 –12x2 +28x 因式分解.当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
解:原式==1、下列从左到右的变形是分解因式的有( )A. 6x2y=3xy·2x
B. a2-b2+1=(a+b)(a-b)+1
C. a2-ab=a(a-b)
D. (x+3)(x-3)= x2-9
C运用拓展2.若多项式-6ab+18abx+24aby的一个因式是
-6ab,那么另一 个因式是( )
(A)-1-3x+4y (B)1+3x-4y
(C)-1-3x-4y (D)1-3x-4yD3.若多项式(a+b)x2+(a+b)x要分解因式,则要提的公因式是 .
(a+b)x4、小明解的有误吗?
当多项式的某一项和公因式相同时,提公因式后剩余的项是1。错误解:抢答我最行!把下列多项式分解因式3a+3b=
5x-5y+5z=
-5a2+25a=
3a2-9ab=3(a+b)5(x-y+z)-5a(a-5)3a(a-3b)?
?
③
把下列各式因式分解:看你能否过关?
a课堂小结:
1、同学们!把你的收获给大家分享 一下!
2、请学科班长评价一下本节课的学习情况!2、确定公因式的方法:
(1)定系数 (2)定字母 (3)定指数小结3、提公因式法因式分解步骤(分两步):
第一步,找出公因式;
第二步,提公因式( 把多项式化为两个因式的乘积)1、什么叫因式分解?4、用提公因式法因式分解应注意的问题:(1)公因式要提尽;
(2)小心漏掉;(3)多项式的首项取正号;(4)公因式是多项式时,要注意符号问题。(1)3.8×0.125+86.2×1/8(2)已知a+b=5,ab=3,求a2b+ab2的值.作业:解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100 =12.5 结果是:15把下列各式分解因式:
1.2a-4b; 2.ax2+ax-4a;
3.3ab2-3a2b; 4.2x3+2x2-6x;
5.7x2+7x+14; 6.-12a2b+24ab2;
7.xy-x2y2-x3y3; 8.27x3+9x2y.练一练拓展题 2、把下列各式因式分解: (1)2m(x+y)+n(x+y);
(2)a(p-q)-4b(q-p);
(3)4a(x-y)2-2b(y-x)2;
(4)2(a-3)2-a+3.
整体思想是数学中一种重要而且常用的思想方法. 公因式既可以是一个单项式的形式,也可以是一个多项式的形式.
