青岛版五年级下册数学期中复习课件(共27张PPT)
文档属性
| 名称 | 青岛版五年级下册数学期中复习课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
数与代数复习梳理
一、整体回顾
异分母分数
加减法
转化
同分母分数
加减法
正负数
认识正负数
用正负数表示具有相反意义的量
分数
意义和性质
分数与除法的关系
分数加减法
真分数和假分数
二、系统梳理
正负数表示具有相反意义的量
正数都大于0,负数都小于0
0既不是正数,也不是负数
正负数
收入200元表示为﹢200元,支出100元表示为-100元。
试一试
1.如果向东50米表示为+50米,那么向西30米表示为 。
-30米
2.如果+100元表示存入100元,那么-120元表示 。
3.如果-0.91元表示某种股票每股下跌的钱数,那么+1.68
元表示 。
支出120元
返回
每股上涨1.68元
二、系统梳理
意义
分数
假分数≥1
把单位“ 1”平均分成若干份,表示这样一份或几份的数。
真分数<1
能化成整数 :
能化成带分数:
基本性质
分数的分子和分母同时乘或除以相同的数(零除外),
分数的大小不变。
大小比较
同分母分数,分子大,分数就大 。
异分母分数
先通分,再比较:
通 分
化成小数比较 :
6
7
6
1
1
8
3
2
9
1
3
2
4
4
5
10
8
19
异分母分数化成同分母分数
5
2
2×3
5×3
15
6
=
=
10
8
8÷2
10÷2
5
4
=
=
2
1
=
6
3
7
6
﹥
7
4
3
2
=
6
4
3
2
=
6
4
2
1
=
6
3
3
2
﹥
2
1
5
1
=0.2
2
1
=0.5
2
1
﹥
5
1
=2
=1
=
=
分类
二、系统梳理
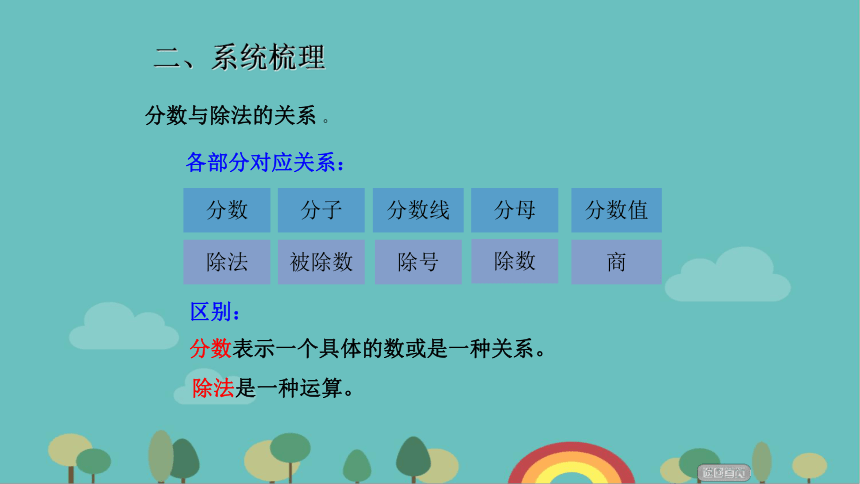
分数与除法的关系 。
各部分对应关系:
区别:
分数表示一个具体的数或是一种关系。
除法是一种运算。
分子
分数线
分母
分数值
被除数
分数
除法
除号
除数
商
二、系统梳理
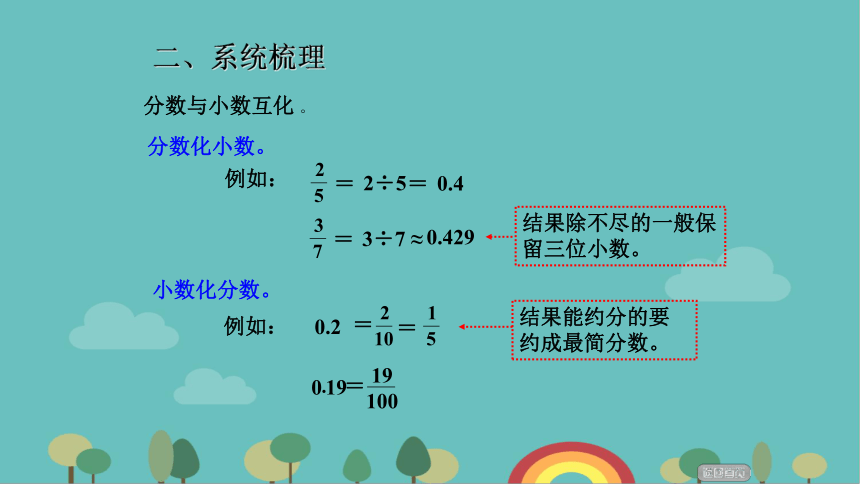
分数与小数互化 。
分数化小数。
小数化分数。
结果除不尽的一般保留三位小数。
5
2
2÷5
=
=
0.4
7
3
3÷7
=
≈
0.429
10
2
0.2
=
5
1
=
100
19
19
.
0
=
例如:
例如:
结果能约分的要约成最简分数。
二、系统梳理
分数加减法。
同分母分数加减法:
异分母分数加减法:
分母不变,分子相加减。
先通分,后加减。
7
3
7
2
7
5
+
=
9
5
-
=
9
2
9
3
=
3
1
7
3
+
=
3
1
21
9
21
7
=
21
16
+
4
3
-
=
3
2
12
9
12
8
=
12
1
-
例如:
例如:
三、综合应用
1.我会填。
(1)我们可以用正负数来表示 的量。
具有相反意义
(2)如果-30元表示支出30元,那么+200元表示
。
存入200元
(3)把7米长的木棒平均分成9段,每段占全长的 ,
每段的长度是 米。
9
1
9
7
46厘米=( )米
50
23
三、综合应用
2.在括号里填上合适的分数。
94分=( )小时
1060米=( )千米
250克=( )千克
30
17
1
50
3
1
4
1
三、综合应用
3.火眼金睛辨对错。
(1)一个数的倍数一定比这个数的因数大。
(2)通分就是把异分母分数转化为同分母分数。
(3)最简分数的分子与分母没有公因数。
(4)因为 比 小,所以 的分数单位比 的分数单位小。
( )
√
×
( )
( )
( )
×
×
5
3
5
3
9
8
9
8
方向与位置复习梳理
整体回顾
表示位置有绝招,一组数据把位标。
左数为列右为行,列先行后不能调。
一列一行一括号,逗号分隔标明了。
确定位置很简单,首先确定观测点。
找准方向和距离,清晰叙述别混乱。
知识梳理
1.数对的含义
在具体情境中,数对可以表
示物体的具体位置。数对
中第一个数表示物体在第
几列,第二个数表示物体在
第几行。
第1列
第2列
第3列
第4列
第5列
第6列
第1行
第2行
第3行
第4行
第5行
(3,2)
给出表示物体在平面图上位置的数对,看数对的两个数表示哪一列、哪一行,行和列的交叉处就是物体的位置或所在区域。
2.用数对表示具体情境中物体位置的方法
(1,5)
(2,4)
(4,3)
(4,5)
(4,1)
(5,4)
给出表示物体在平面图上位置
的数对,看数对的两个数表示哪
一列、哪一行,行和列的交叉处
就是物体的位置或所在区域。
3.根据数对在方格纸上找到相应的位置
5
4
3
2
1
0 1 2 3 4 5 6
小强(3,2)
·
先找准方向、确定角度;再确定被测点到观测点的实际距离,根据方向和距离准确描述物体的位置。
4.根据方向和距离确定位置
向东走300m
南偏东50°450m
北偏东50°320m
向东走600m
学校
书店
电厂
公园
少年宫
北
综合运用
1.观察下图并填空。
(2)星期天,小明的活动路线是(7,4)→(4,4)→(5,5)→(2,7)→(7,8),小明从( )出发,途经( )、( )、( ),到达( )。
思路分析:
如果是根据数对找位置,就依据数对找图上列与行的交叉点。
家
少年宫
公园
邮局
商场
2.一艘快船从甲港开往乙港,航行路线如下图。
(1)说一说这艘快船从甲港到乙
港的航行路线。
描述路线时,从出发点甲港开始,就以甲港为观测点,
途经A,就根据A相对于甲港的位置确定要走的方向和
距离;从A到B,是以A为观测点,根据B相对于A的位置
确定要走的方向和距离;从B到乙港,是以B为观测点,
根据乙港相对于B的位置确定要走的方向和距离。
2.一艘快船从甲港开往乙港,航行路线如下图。
(1)说一说这艘快船从甲港到乙
港的航行路线。
从甲港向北偏东60°方向航行100海里到A
点;从A点向正北方向航行70海里到B点;从B
点向北偏东45°方向航行150海里到达乙港。
2.一艘快船从甲港开往乙港,航行路线如下图。
(2)如果这艘船每小时航行50海里,
从甲港到乙港共需多少小时
算出甲港到乙港的总路程,根据
“路程÷速度=时间”计算。
(100+70+150)÷50=6.4(时)
答:从甲港到乙港共需6.4小时。
问题反馈
主要有:
1.概念掌握不清,无法灵活应用(分数的意义,分数的基本性质)
2.审题不清
3.书写问题(带分数的规范写法;单位;答语过于简单)
4.计算过程规范书写,计算结果约分化简
活动要求
1、自主纠错(10分钟左右)
要求:
1.红笔,独立修改,写出解题过程,自己解决不了的做好标记,准备合作探究。
2.过程中注意将自己的错题进行归类,归类参考:
分数的意义;
分数与除法的关系;
分数的分类及换算;
公因数,公倍数及约分;
分数加减法
2、合作探究(12——15分钟)
A主持让每位同学说说自己未解决的疑难问题,进行统计,然后将错题归类并按类别讲解方法。
要求:
1.组内先两两合作再四人讨论,都不会的标记好问题。
2.重点讨论疑难问题的分析思路与方法,总结出解决问题的一般策略。
A帮B B帮C
建议重点展示以下问题:
根据分数的意义及分数与除法的关系解决实际问题(一、4.;五1.2.)
分数的分类及换算(一、3.6.9);
公因数,公倍数及约分(一、8.;五、5.);
分数加减法(四、5。最后一题;五、4.5.)
展示交流(12——15分钟)
整理落实
将易错题、疑难问题整理到典型习题集上,注意归类,总结方法
回顾反思
数与代数复习梳理
一、整体回顾
异分母分数
加减法
转化
同分母分数
加减法
正负数
认识正负数
用正负数表示具有相反意义的量
分数
意义和性质
分数与除法的关系
分数加减法
真分数和假分数
二、系统梳理
正负数表示具有相反意义的量
正数都大于0,负数都小于0
0既不是正数,也不是负数
正负数
收入200元表示为﹢200元,支出100元表示为-100元。
试一试
1.如果向东50米表示为+50米,那么向西30米表示为 。
-30米
2.如果+100元表示存入100元,那么-120元表示 。
3.如果-0.91元表示某种股票每股下跌的钱数,那么+1.68
元表示 。
支出120元
返回
每股上涨1.68元
二、系统梳理
意义
分数
假分数≥1
把单位“ 1”平均分成若干份,表示这样一份或几份的数。
真分数<1
能化成整数 :
能化成带分数:
基本性质
分数的分子和分母同时乘或除以相同的数(零除外),
分数的大小不变。
大小比较
同分母分数,分子大,分数就大 。
异分母分数
先通分,再比较:
通 分
化成小数比较 :
6
7
6
1
1
8
3
2
9
1
3
2
4
4
5
10
8
19
异分母分数化成同分母分数
5
2
2×3
5×3
15
6
=
=
10
8
8÷2
10÷2
5
4
=
=
2
1
=
6
3
7
6
﹥
7
4
3
2
=
6
4
3
2
=
6
4
2
1
=
6
3
3
2
﹥
2
1
5
1
=0.2
2
1
=0.5
2
1
﹥
5
1
=2
=1
=
=
分类
二、系统梳理
分数与除法的关系 。
各部分对应关系:
区别:
分数表示一个具体的数或是一种关系。
除法是一种运算。
分子
分数线
分母
分数值
被除数
分数
除法
除号
除数
商
二、系统梳理
分数与小数互化 。
分数化小数。
小数化分数。
结果除不尽的一般保留三位小数。
5
2
2÷5
=
=
0.4
7
3
3÷7
=
≈
0.429
10
2
0.2
=
5
1
=
100
19
19
.
0
=
例如:
例如:
结果能约分的要约成最简分数。
二、系统梳理
分数加减法。
同分母分数加减法:
异分母分数加减法:
分母不变,分子相加减。
先通分,后加减。
7
3
7
2
7
5
+
=
9
5
-
=
9
2
9
3
=
3
1
7
3
+
=
3
1
21
9
21
7
=
21
16
+
4
3
-
=
3
2
12
9
12
8
=
12
1
-
例如:
例如:
三、综合应用
1.我会填。
(1)我们可以用正负数来表示 的量。
具有相反意义
(2)如果-30元表示支出30元,那么+200元表示
。
存入200元
(3)把7米长的木棒平均分成9段,每段占全长的 ,
每段的长度是 米。
9
1
9
7
46厘米=( )米
50
23
三、综合应用
2.在括号里填上合适的分数。
94分=( )小时
1060米=( )千米
250克=( )千克
30
17
1
50
3
1
4
1
三、综合应用
3.火眼金睛辨对错。
(1)一个数的倍数一定比这个数的因数大。
(2)通分就是把异分母分数转化为同分母分数。
(3)最简分数的分子与分母没有公因数。
(4)因为 比 小,所以 的分数单位比 的分数单位小。
( )
√
×
( )
( )
( )
×
×
5
3
5
3
9
8
9
8
方向与位置复习梳理
整体回顾
表示位置有绝招,一组数据把位标。
左数为列右为行,列先行后不能调。
一列一行一括号,逗号分隔标明了。
确定位置很简单,首先确定观测点。
找准方向和距离,清晰叙述别混乱。
知识梳理
1.数对的含义
在具体情境中,数对可以表
示物体的具体位置。数对
中第一个数表示物体在第
几列,第二个数表示物体在
第几行。
第1列
第2列
第3列
第4列
第5列
第6列
第1行
第2行
第3行
第4行
第5行
(3,2)
给出表示物体在平面图上位置的数对,看数对的两个数表示哪一列、哪一行,行和列的交叉处就是物体的位置或所在区域。
2.用数对表示具体情境中物体位置的方法
(1,5)
(2,4)
(4,3)
(4,5)
(4,1)
(5,4)
给出表示物体在平面图上位置
的数对,看数对的两个数表示哪
一列、哪一行,行和列的交叉处
就是物体的位置或所在区域。
3.根据数对在方格纸上找到相应的位置
5
4
3
2
1
0 1 2 3 4 5 6
小强(3,2)
·
先找准方向、确定角度;再确定被测点到观测点的实际距离,根据方向和距离准确描述物体的位置。
4.根据方向和距离确定位置
向东走300m
南偏东50°450m
北偏东50°320m
向东走600m
学校
书店
电厂
公园
少年宫
北
综合运用
1.观察下图并填空。
(2)星期天,小明的活动路线是(7,4)→(4,4)→(5,5)→(2,7)→(7,8),小明从( )出发,途经( )、( )、( ),到达( )。
思路分析:
如果是根据数对找位置,就依据数对找图上列与行的交叉点。
家
少年宫
公园
邮局
商场
2.一艘快船从甲港开往乙港,航行路线如下图。
(1)说一说这艘快船从甲港到乙
港的航行路线。
描述路线时,从出发点甲港开始,就以甲港为观测点,
途经A,就根据A相对于甲港的位置确定要走的方向和
距离;从A到B,是以A为观测点,根据B相对于A的位置
确定要走的方向和距离;从B到乙港,是以B为观测点,
根据乙港相对于B的位置确定要走的方向和距离。
2.一艘快船从甲港开往乙港,航行路线如下图。
(1)说一说这艘快船从甲港到乙
港的航行路线。
从甲港向北偏东60°方向航行100海里到A
点;从A点向正北方向航行70海里到B点;从B
点向北偏东45°方向航行150海里到达乙港。
2.一艘快船从甲港开往乙港,航行路线如下图。
(2)如果这艘船每小时航行50海里,
从甲港到乙港共需多少小时
算出甲港到乙港的总路程,根据
“路程÷速度=时间”计算。
(100+70+150)÷50=6.4(时)
答:从甲港到乙港共需6.4小时。
问题反馈
主要有:
1.概念掌握不清,无法灵活应用(分数的意义,分数的基本性质)
2.审题不清
3.书写问题(带分数的规范写法;单位;答语过于简单)
4.计算过程规范书写,计算结果约分化简
活动要求
1、自主纠错(10分钟左右)
要求:
1.红笔,独立修改,写出解题过程,自己解决不了的做好标记,准备合作探究。
2.过程中注意将自己的错题进行归类,归类参考:
分数的意义;
分数与除法的关系;
分数的分类及换算;
公因数,公倍数及约分;
分数加减法
2、合作探究(12——15分钟)
A主持让每位同学说说自己未解决的疑难问题,进行统计,然后将错题归类并按类别讲解方法。
要求:
1.组内先两两合作再四人讨论,都不会的标记好问题。
2.重点讨论疑难问题的分析思路与方法,总结出解决问题的一般策略。
A帮B B帮C
建议重点展示以下问题:
根据分数的意义及分数与除法的关系解决实际问题(一、4.;五1.2.)
分数的分类及换算(一、3.6.9);
公因数,公倍数及约分(一、8.;五、5.);
分数加减法(四、5。最后一题;五、4.5.)
展示交流(12——15分钟)
整理落实
将易错题、疑难问题整理到典型习题集上,注意归类,总结方法
回顾反思
同课章节目录
