2023-2024学年湖南省衡阳市衡山县部分学校期中联考试题卷(含解析)八年级上册数学
文档属性
| 名称 | 2023-2024学年湖南省衡阳市衡山县部分学校期中联考试题卷(含解析)八年级上册数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 712.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览



文档简介
八年级数学(问卷)
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题共10小题,每小题4分,共40分。每小题只有1个选项符合题意。请将符合题意的选项用2B铅笔填涂在答题卡相应位置)
1.下列式子中是分式的是( )
A. B. C. D.
2.7的平方根是( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.一棵小草一天能释放的氧气是微乎其微的,每平方米的绿草每天可以放出大约0.015千克的氧气,同时吸收二氧化碳和灰尘,减少空气中的细菌含量,净化空气.用科学记数法表示0.015为( )
A. B. C. D.
5.若方程的根为,则m的值是( )
A.0 B.3 C. D.1
6.中国5G技术世界领先,安乡县将逐步推动5G网络全覆盖,5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输4千兆数据,5G网络比4G网络快90秒.若设4G网络的峰值速率为每秒传输千兆数据,则由题意可列方程为( )
A. B. C. D.
7.下列三条线段中,能够首尾相接构成一个三角形的是( )
A.,, B.,, C.,, D.,,
8.如图,小亮书上的三角形被墨迹污染了一部分,他根据所学全等三角形的知识很快就画了一个与书上完全一样的三角形,那么小亮画图的依据是( )
A. B. C. D.
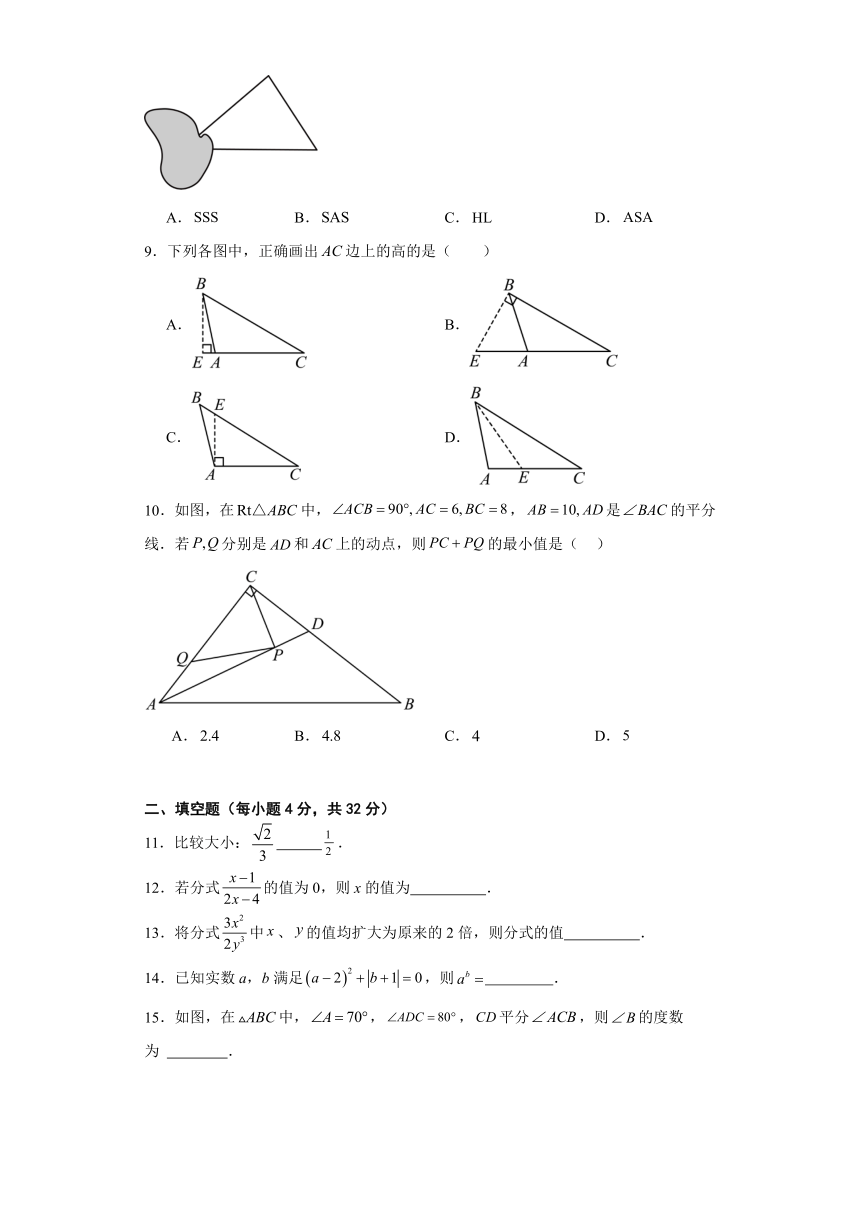
9.下列各图中,正确画出边上的高的是( )
A. B.
C. D.
10.如图,在中,,是的平分线.若分别是和上的动点,则的最小值是( )
A. B. C. D.
二、填空题(每小题4分,共32分)
11.比较大小: .
12.若分式的值为0,则x的值为 .
13.将分式中、的值均扩大为原来的2倍,则分式的值 .
14.已知实数a,b满足,则 .
15.如图,在中,,,平分,则的度数为 .
16.某车间加工12个零件后,采用新工艺,工效比原来提高了50%,这样加工同样多的零件就少用1小时,那么采用新工艺前每小时加工 个零件.
17.如图,点是内部的一点,连接,已知,,一只小蚂蚁从点出发爬到边上任意一点,再爬到边上任意一点,然后爬回点处,则小蚂蚁爬行的路径最短为
18.如图,C为线段上一动点(不与点A,E重合),在同侧分别作等边和等边,与交于点O,与交于点P,与交于点Q,连结.以下五个结论:①;②;③;④为等边三角形;⑤.其中正确的有 .(注:把你认为正确的答案序号都写上)
三、解答题(共8个小题,共78分)
19.计算:.
先化简再求值,,其中.
已知实数a,b,c,d,e,f,且a,b互为倒数,c,d互为相反数,e的绝对值为,f的算术平方根是8,求的平方根.
《非机动车管理办法》规定:电动自行车驾驶人和乘坐人员应该戴安全头盔.某商店用1600元购进一批电动车头盔,销售发现供不应求,于是,又用5400元再购进一批头盔,第二批头盔的数量是第一批的3倍,但单价比第一批贵10元.第一批头盔进货单价多少元
23.如图,在中,点P为边上一点.
(1)尺规作图:请在上求作一点D,使得(保留作图痕迹,不写作法).
(2)在(1)的条件下,,,求证:是等边三角形.
24.在中,,,平分,于点,求的度数.
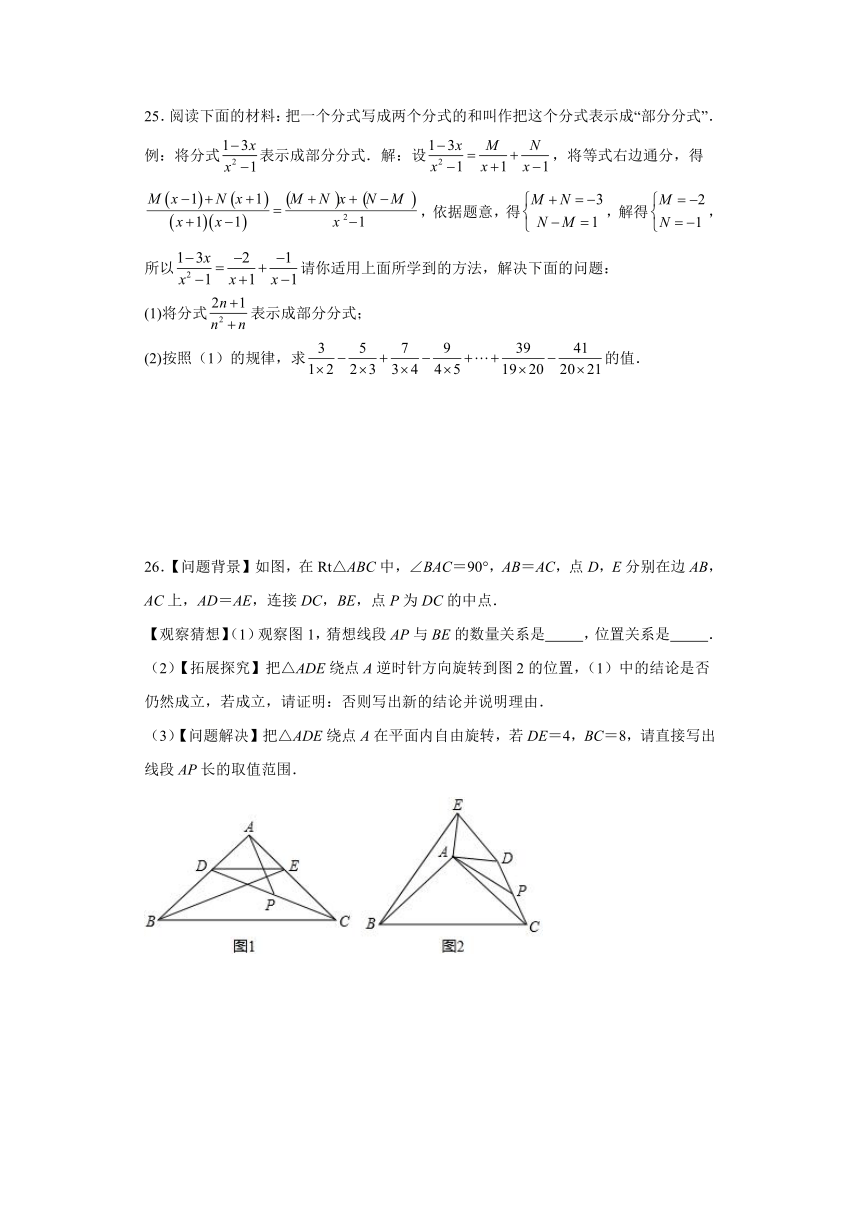
25.阅读下面的材料:把一个分式写成两个分式的和叫作把这个分式表示成“部分分式”.
例:将分式表示成部分分式.解:设,将等式右边通分,得
,依据题意,得,解得,所以请你适用上面所学到的方法,解决下面的问题:
(1)将分式表示成部分分式;
(2)按照(1)的规律,求的值.
26.【问题背景】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,BE,点P为DC的中点.
【观察猜想】(1)观察图1,猜想线段AP与BE的数量关系是 ,位置关系是 .
(2)【拓展探究】把△ADE绕点A逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立,请证明:否则写出新的结论并说明理由.
(3)【问题解决】把△ADE绕点A在平面内自由旋转,若DE=4,BC=8,请直接写出线段AP长的取值范围.
试卷第1页,共3页
参考答案
1.B 2.C 3.C 4.C 5.C 6.B 7.C 8.D 9.A 10.B
11. 12.1 13.缩小到原来的 14. 15./度 16.4
17./9厘米 18.①②④⑤
19.0
【分析】本题考查了幂的混合运算,利用同底数幂的除法运算法则及积的乘方即可求解,熟练掌握相关运算法则是解题的关键.
【详解】解:原式
.
20.,2
【分析】本题考查的是分式的化简求值,先根据分式的运算法则进行化简,再代入求值即可.
【详解】解:,
,
把代入得,原式.
21.
【分析】根据倒数,相反数,绝对值,算术平方根的意义可得然后代入式子中进行计算即可解答.
【详解】解:由题意可知:,,,,
所以,,
所以,所以8的平方根为
【提醒】本题考查了实数的运算,熟练掌握倒数,相反数,绝对值,算术平方根,立方根的意义是解题的关键.
22.80
【分析】设第一批头盔进货单价x元,则第二批进价为元,再根据等量关系“第二批头盔的数量是第一批的3倍”列分式方程求解即可.
【详解】解:设第一批头盔进货单价x元,则第二批进价为元,
根据题意可得:,解得:,
经检验,是分式方程的解,
答:第一批头盔进货单价80元.
【提醒】本题主要考查了分式方程的应用,根据题意、正确列出分式方程是解答本题的关键.
23.(1)见解析
(2)见解析
【分析】(1)利用利用同位角相等两条直线平行作,则即为所求;
(2)利用等边对等角得到,利用平行线得到,再根据三角形的内角和得到,即可得到结论.
【详解】(1))如图所示:
利用同位角相等两条直线平行作则即为所求.
(2)
,
∵
,
∴,
,
为等边三角形.
【提醒】本题考查平行线的作图,等边三角形的判定,等腰三角形的性质,掌握等边三角形的判定定理是解题的关键.
24..
【分析】根据三角形内角和定理得出,根据角平分线的定义以及三角形的外角的性质得出,进而根据,得出,即可求解.
【详解】∵在中,,,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴.
【提醒】此题考查了三角形内角和定理,以及三角形的外角的性质,垂直的定义,熟练掌握三角形内角和定理是解题的关键.
25.(1),见解析.
(2).
【分析】(1)模仿阅读材料可得答案;
(2)根据(1)的规律变形,再计算即可.
【详解】(1)解:设,
∴,
∴,
∴.
(2)
;
【提醒】本题考查分式的混合运算,解题的关键是读懂题意,能把一个分式化为部分分式.
26.(1)AP=BE,PA⊥BE;(2)成立,证明见解析;(3)
【分析】(1)如图1中,设PA交BE于点O.证明△DAC≌△EAB(SAS),结合直角三角形斜边中线的性质即可解决问题.
(2)结论成立.如图2中,延长AP到J,使得PJ=PA,连接JC.延长PA交BE于O.证明△EAB≌△JCA(SAS),即可解决问题.
(3)利用三角形的三边关系求出AJ的取值范围,即可解决问题.
【详解】解:(1)如图1中,设PA交BE于点O.
∵AD=AE,AC=AB,∠DAC=∠EAB,
∴△DAC≌△EAB(SAS),
∴BE=CD,∠ACD=∠ABE,
∵∠DAC=90°,DP=PC,
∴PA=CD=PC=PD,
∴PA=BE.∠C=∠PAE,
∵∠CAP+∠BAO=90°,
∴∠ABO+∠BAO=90°,
∴∠AOB=90°,
∴PA⊥BE,
故答案为:AP=BE,PA⊥BE.
(2)结论成立.
理由:如图2中,延长AP到J,使得PJ=PA,连接JC.延长PA交BE于O.
∵PA=PJ,PD=PC,∠APD=∠CPJ,
∴△APD≌△JPC(SAS),
∴AD=CJ,∠ADP=∠JCP,
∴AD∥CJ,
∴∠DAC+∠ACJ=180°,
∵∠BAC=∠EAD=90°,
∴∠EAB+∠DAC=180°,
∴∠EAB=∠ACJ,
∵AB=AC,AE=AD=CJ,
∴△EAB≌△JCA(SAS),
∴BE=AJ,∠CAJ=∠ABE,
∵PA=AJ,
∴PA=BE,
∵∠CAJ+∠BAO=90°,
∴∠ABE+∠BAO=90°,
∴∠AOB=90°,
∴PA⊥BE.
(3)∵△AED,△ABC都是等腰三角形,DE=4,BC=8,
∴AD=AE=2,AC=AB=4
由(2)可知CJ=AD=2,∵AC=4,
∴4﹣2≤AJ≤4+2,
∴2≤AJ≤6,
∵AJ=2AP,
∴≤PA≤3.
【提醒】本题综合考查了全等三角形的判定和性质,等腰三角形的判定和性质,直角三角形斜边上的中线的性质,以及三角形的三边关系,熟悉并灵活运用以上性质是解题的关键.
答案第1页,共2页
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题共10小题,每小题4分,共40分。每小题只有1个选项符合题意。请将符合题意的选项用2B铅笔填涂在答题卡相应位置)
1.下列式子中是分式的是( )
A. B. C. D.
2.7的平方根是( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.一棵小草一天能释放的氧气是微乎其微的,每平方米的绿草每天可以放出大约0.015千克的氧气,同时吸收二氧化碳和灰尘,减少空气中的细菌含量,净化空气.用科学记数法表示0.015为( )
A. B. C. D.
5.若方程的根为,则m的值是( )
A.0 B.3 C. D.1
6.中国5G技术世界领先,安乡县将逐步推动5G网络全覆盖,5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输4千兆数据,5G网络比4G网络快90秒.若设4G网络的峰值速率为每秒传输千兆数据,则由题意可列方程为( )
A. B. C. D.
7.下列三条线段中,能够首尾相接构成一个三角形的是( )
A.,, B.,, C.,, D.,,
8.如图,小亮书上的三角形被墨迹污染了一部分,他根据所学全等三角形的知识很快就画了一个与书上完全一样的三角形,那么小亮画图的依据是( )
A. B. C. D.
9.下列各图中,正确画出边上的高的是( )
A. B.
C. D.
10.如图,在中,,是的平分线.若分别是和上的动点,则的最小值是( )
A. B. C. D.
二、填空题(每小题4分,共32分)
11.比较大小: .
12.若分式的值为0,则x的值为 .
13.将分式中、的值均扩大为原来的2倍,则分式的值 .
14.已知实数a,b满足,则 .
15.如图,在中,,,平分,则的度数为 .
16.某车间加工12个零件后,采用新工艺,工效比原来提高了50%,这样加工同样多的零件就少用1小时,那么采用新工艺前每小时加工 个零件.
17.如图,点是内部的一点,连接,已知,,一只小蚂蚁从点出发爬到边上任意一点,再爬到边上任意一点,然后爬回点处,则小蚂蚁爬行的路径最短为
18.如图,C为线段上一动点(不与点A,E重合),在同侧分别作等边和等边,与交于点O,与交于点P,与交于点Q,连结.以下五个结论:①;②;③;④为等边三角形;⑤.其中正确的有 .(注:把你认为正确的答案序号都写上)
三、解答题(共8个小题,共78分)
19.计算:.
先化简再求值,,其中.
已知实数a,b,c,d,e,f,且a,b互为倒数,c,d互为相反数,e的绝对值为,f的算术平方根是8,求的平方根.
《非机动车管理办法》规定:电动自行车驾驶人和乘坐人员应该戴安全头盔.某商店用1600元购进一批电动车头盔,销售发现供不应求,于是,又用5400元再购进一批头盔,第二批头盔的数量是第一批的3倍,但单价比第一批贵10元.第一批头盔进货单价多少元
23.如图,在中,点P为边上一点.
(1)尺规作图:请在上求作一点D,使得(保留作图痕迹,不写作法).
(2)在(1)的条件下,,,求证:是等边三角形.
24.在中,,,平分,于点,求的度数.
25.阅读下面的材料:把一个分式写成两个分式的和叫作把这个分式表示成“部分分式”.
例:将分式表示成部分分式.解:设,将等式右边通分,得
,依据题意,得,解得,所以请你适用上面所学到的方法,解决下面的问题:
(1)将分式表示成部分分式;
(2)按照(1)的规律,求的值.
26.【问题背景】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,BE,点P为DC的中点.
【观察猜想】(1)观察图1,猜想线段AP与BE的数量关系是 ,位置关系是 .
(2)【拓展探究】把△ADE绕点A逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立,请证明:否则写出新的结论并说明理由.
(3)【问题解决】把△ADE绕点A在平面内自由旋转,若DE=4,BC=8,请直接写出线段AP长的取值范围.
试卷第1页,共3页
参考答案
1.B 2.C 3.C 4.C 5.C 6.B 7.C 8.D 9.A 10.B
11. 12.1 13.缩小到原来的 14. 15./度 16.4
17./9厘米 18.①②④⑤
19.0
【分析】本题考查了幂的混合运算,利用同底数幂的除法运算法则及积的乘方即可求解,熟练掌握相关运算法则是解题的关键.
【详解】解:原式
.
20.,2
【分析】本题考查的是分式的化简求值,先根据分式的运算法则进行化简,再代入求值即可.
【详解】解:,
,
把代入得,原式.
21.
【分析】根据倒数,相反数,绝对值,算术平方根的意义可得然后代入式子中进行计算即可解答.
【详解】解:由题意可知:,,,,
所以,,
所以,所以8的平方根为
【提醒】本题考查了实数的运算,熟练掌握倒数,相反数,绝对值,算术平方根,立方根的意义是解题的关键.
22.80
【分析】设第一批头盔进货单价x元,则第二批进价为元,再根据等量关系“第二批头盔的数量是第一批的3倍”列分式方程求解即可.
【详解】解:设第一批头盔进货单价x元,则第二批进价为元,
根据题意可得:,解得:,
经检验,是分式方程的解,
答:第一批头盔进货单价80元.
【提醒】本题主要考查了分式方程的应用,根据题意、正确列出分式方程是解答本题的关键.
23.(1)见解析
(2)见解析
【分析】(1)利用利用同位角相等两条直线平行作,则即为所求;
(2)利用等边对等角得到,利用平行线得到,再根据三角形的内角和得到,即可得到结论.
【详解】(1))如图所示:
利用同位角相等两条直线平行作则即为所求.
(2)
,
∵
,
∴,
,
为等边三角形.
【提醒】本题考查平行线的作图,等边三角形的判定,等腰三角形的性质,掌握等边三角形的判定定理是解题的关键.
24..
【分析】根据三角形内角和定理得出,根据角平分线的定义以及三角形的外角的性质得出,进而根据,得出,即可求解.
【详解】∵在中,,,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴.
【提醒】此题考查了三角形内角和定理,以及三角形的外角的性质,垂直的定义,熟练掌握三角形内角和定理是解题的关键.
25.(1),见解析.
(2).
【分析】(1)模仿阅读材料可得答案;
(2)根据(1)的规律变形,再计算即可.
【详解】(1)解:设,
∴,
∴,
∴.
(2)
;
【提醒】本题考查分式的混合运算,解题的关键是读懂题意,能把一个分式化为部分分式.
26.(1)AP=BE,PA⊥BE;(2)成立,证明见解析;(3)
【分析】(1)如图1中,设PA交BE于点O.证明△DAC≌△EAB(SAS),结合直角三角形斜边中线的性质即可解决问题.
(2)结论成立.如图2中,延长AP到J,使得PJ=PA,连接JC.延长PA交BE于O.证明△EAB≌△JCA(SAS),即可解决问题.
(3)利用三角形的三边关系求出AJ的取值范围,即可解决问题.
【详解】解:(1)如图1中,设PA交BE于点O.
∵AD=AE,AC=AB,∠DAC=∠EAB,
∴△DAC≌△EAB(SAS),
∴BE=CD,∠ACD=∠ABE,
∵∠DAC=90°,DP=PC,
∴PA=CD=PC=PD,
∴PA=BE.∠C=∠PAE,
∵∠CAP+∠BAO=90°,
∴∠ABO+∠BAO=90°,
∴∠AOB=90°,
∴PA⊥BE,
故答案为:AP=BE,PA⊥BE.
(2)结论成立.
理由:如图2中,延长AP到J,使得PJ=PA,连接JC.延长PA交BE于O.
∵PA=PJ,PD=PC,∠APD=∠CPJ,
∴△APD≌△JPC(SAS),
∴AD=CJ,∠ADP=∠JCP,
∴AD∥CJ,
∴∠DAC+∠ACJ=180°,
∵∠BAC=∠EAD=90°,
∴∠EAB+∠DAC=180°,
∴∠EAB=∠ACJ,
∵AB=AC,AE=AD=CJ,
∴△EAB≌△JCA(SAS),
∴BE=AJ,∠CAJ=∠ABE,
∵PA=AJ,
∴PA=BE,
∵∠CAJ+∠BAO=90°,
∴∠ABE+∠BAO=90°,
∴∠AOB=90°,
∴PA⊥BE.
(3)∵△AED,△ABC都是等腰三角形,DE=4,BC=8,
∴AD=AE=2,AC=AB=4
由(2)可知CJ=AD=2,∵AC=4,
∴4﹣2≤AJ≤4+2,
∴2≤AJ≤6,
∵AJ=2AP,
∴≤PA≤3.
【提醒】本题综合考查了全等三角形的判定和性质,等腰三角形的判定和性质,直角三角形斜边上的中线的性质,以及三角形的三边关系,熟悉并灵活运用以上性质是解题的关键.
答案第1页,共2页
同课章节目录
