期中经典题型检测卷2023-2024学年数学五年级下册苏教版(含答案)
文档属性
| 名称 | 期中经典题型检测卷2023-2024学年数学五年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 459.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 16:13:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中经典题型检测卷2023-2024学年数学五年级下册苏教版
一、选择题
1.折线统计图的特点是( )。
A.表示数量的多少 B.表示数量的增减变化
C.既表示数量的多少又表示数量的增减变化 D.以上答案都不正确
2.35÷□=4……3,如果商用分数表示是( )。
A. B. C. D.
3.汾河湿地公园的一段水域上生活有野鸭114只,比白鹭数量的3倍少30只。设白鹭的数量是x只,下列方程错误的是( )。
A.3x-30=114 B.114-3x=30 C.3x-114=30 D.3x=114+30
4.用1、2、3这三个数字组成的三位数一定是( )的倍数。
A.2 B.3 C.2或3 D.4
5.两堆黄沙一样重,第一堆运走吨,第二堆运走了它的,运走的黄沙相比( )。
A.第一堆多 B.第二堆多 C.一样多 D.无法确定
6.一根1米长的绳子,连续对折4次,每段长( )米。
A. B. C. D.
二、填空题
7.7厘米=分米 17千克=吨 73分=小时
8.一个两位数3,它既有因数2,又是3的倍数,里的能填的数最大是( ),把这个两位数分解质因数是( )。
9.( )统计图不仅能够表示出数量的多少,还能反映数量的增减变化情况。
10.有三个连续的偶数,若中间一个数是m,那么比m大的数是( );如果这三个数的平均数是18,则最小的数是( )。
11.买2支钢笔和3瓶墨水共付13.5元,买同样的3支钢笔和5瓶墨水共付21.5元。一支钢笔( )元,一瓶墨水的单价是( )元。
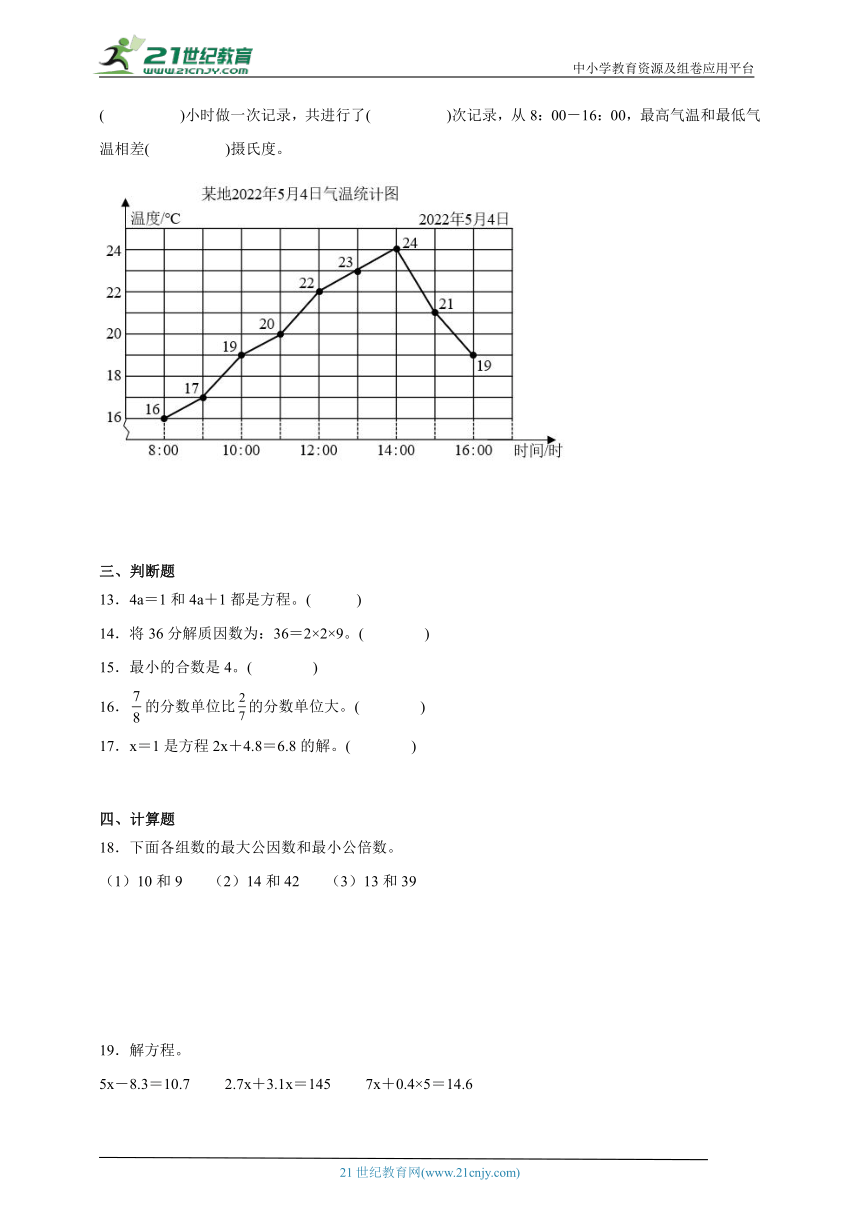
12.小明对5月4日的气温进行了记录,并制成了统计图(如下图),从统计图中可以看出,他每隔( )小时做一次记录,共进行了( )次记录,从8:00-16:00,最高气温和最低气温相差( )摄氏度。
三、判断题
13.4a=1和4a+1都是方程。( )
14.将36分解质因数为:36=2×2×9。( )
15.最小的合数是4。( )
16.的分数单位比的分数单位大。( )
17.x=1是方程2x+4.8=6.8的解。( )
四、计算题
18.下面各组数的最大公因数和最小公倍数。
(1)10和9 (2)14和42 (3)13和39
19.解方程。
5x-8.3=10.7 2.7x+3.1x=145 7x+0.4×5=14.6
20.看图列方程并解答。
五、解答题
21.在一次跳高比赛中,小杰跳了1米,小东跳了1.15米,小军跳了米,请你给他们排个名次?
22.一个长方形长45厘米,宽36厘米,把它剪成相等的小正方形,不能有剩余,剪成的小正方形的边长最大是多少厘米?共能剪成多少块?
23.两路公交车,甲车每4分钟发一班,乙车每5分钟发一班,它们从7:20第一次同时发车后,至少再过多少分钟两车第二次同时发车?是几时几分?
24.甲、乙两城相距360千米,一辆汽车从甲城开往乙城,一辆摩托车同时从乙城开往甲城。摩托车每小时行驶45千米,3小时后两车相遇。汽车每小时行驶多少千米?(列方程解答)
25.上海东方明珠广播电视塔高468米,比号称“徐州之巅”的徐州苏宁广场主塔楼高的2倍少64米,徐州苏宁广场主塔楼高多少米?(用方程解答)
26.新时代商场2022年下半年空调和冰箱的销售情况如表所示:
月份 销量 商品 7 8 9 10 11 12
空调 450 750 550 350 300 600
冰箱 300 500 350 300 250 200
(1)根据上表中的数据制成折线统计图。
(2)商场下半年平均每月销售空调多少台?
(3)如果每台冰箱的利润是150元,那么这个商场2022年第三季度冰箱共获利多少万元?
参考答案:
1.C
【分析】折线统计图可以表示数量的增减变化;条形统计图可以表示数量的多少。
【详解】根据分析可知,折线统计图的特点是表示数量的增减变化。
【点睛】考查折线统计图的特点是表示数量的增减变化。
2.B
【分析】根据除数=(被除数-余数)÷商,求出□中的除数,再根据除法与分数的关系计算出商,据此解答。
【详解】(35-3)÷4
=32÷4
=8
35÷8=
35÷□=4……3,如果商用分数表示是。
故答案为:B
【点睛】本题考查被除数、除数、商和余数之间的关系,以及除法与分数的关系。
3.B
【分析】设白鹭的数量是x只,野鸭的数量比白鹭的3倍少30只,即白鹭的只数×3-30=野鸭的只数,野鸭只数有114只,列方程:3x-30=114,据此分析,进行解答。
【详解】设白鹭的数量是x只。则:
3x-30=114
3x-114=30
3x=114+30
汾河湿地公园的一段水域上生活有野鸭114只,比白鹭数量的3倍少30只。设白鹭的数量是x只,下列方程错误的是114-3x=30。
故答案为:B
【点睛】解答本题的关键是根据题意,找清楚野鸭和白鹭数量之间的关系,进而解答。
4.B
【分析】先写出1、2、3可以组成的三位数,再根据2、3、5的倍数特征进行判断;
2的倍数特征:个位上是0、2、4、6、8的数;
5的倍数特征:个位上是0或5的数;
3的倍数特征:各个数位之和能够被3整数。
【详解】1、2、3组成的三位数有123、132、213、231、321、312;
1、2、3组成的三位数都不是5的倍数;
123、213、231、321都不是2的倍数,也不是4的倍数;
1+2+3=6,6能被3整除,是3的倍数;组成的三位数一定是3的倍数。
用1、2、3这三个数字组成的三位数一定是3的倍数。
故答案为:B
【点睛】熟练掌握2、3、5的倍数特征是解答本题的关键。
5.D
【分析】如果这两堆黄沙都是1吨,1吨的就是吨,两堆运走的一样重,剩下的也一样重;如果这两堆黄沙都不足1吨,不足1吨的就小于吨,第一堆运走的重;如果这两堆黄沙都大于1吨,大于1吨的就大于吨,第二堆运走的重;据此可解。
【详解】当这两堆黄沙都是1吨,1×=,吨=吨,两堆运走的一样重;
当这两堆黄沙都不足1吨,假设为0.3吨时,0.3×=0.1,0.1吨<吨,因此第一堆运走的重;
当这两堆黄沙都大于1吨,假设为3吨时,3×=1,1吨>吨,因此第二堆运走的重;
这两堆黄沙的质量不确定,剩下的黄沙重量相比较,无法确定哪堆重。
故答案为:D
【点睛】第一堆运走的吨是一个具体的量,而第二堆运走的是一个分率,只有在确定了这堆黄沙质量的情况下才能确定它的质量,因此,在不确定黄沙质量的情况下,无法确定它的质量。
6.D
【分析】第一次对折后,就是把绳子平均分成2份,第二次对折后,就是把绳子平均分成 4份,第三次对折后,就是把绳子平均分成8份,第四次对折后,就是把绳子平均分成16分,求每段长,用绳子的长度1÷16解答。
【详解】根据分析可知,对折4次,把绳子平均分成16份。
1÷16=(米)
一根1米长的绳子,连续对折4次,每段长米。
故答案为:D
【点睛】解答本题的关键是明确对折4次就是把绳子平均分成16份。
7.;;
【分析】根据1分米=10厘米,1吨=1000千克,1小时=60分钟,高级单位化低级单位要乘进率,低级单位化高级单位要除以进率,据此解答。
【详解】7厘米=分米
17千克=吨
73分=小时
【点睛】本题考查了长度单位、质量单位、时间单位的换算,明确高级单位化低级单位要乘进率,低级单位化高级单位要除以进率。
8. 6 36=2×2×3×3
【分析】根据2、3的倍数的特征:个位数是0、2、4、6、8是都是2的倍数;一个数各数位上的数字之和是3的倍数,这个数一定是3的倍数。因此,既有因数2,又是3的倍数,里的能填的数最大是6,再把36分解质因数即可。
【详解】一个两位数3,它既有因数2,又是3的倍数,里的能填的数最大是(6),把这个两位数分解质因数是(36=2×2×3×3)。
【点睛】掌握能被2、3整除的数的特征是解答此题的关键。
9.折线
【详解】折线统计图不仅能够表示出数量的多少,还能反映数量的增减变化情况。例如:
折线统计图不仅表示1年内每个月的平均温度,也可以看出每个月温度的变化。
10. 2+m/ m+2 16
【分析】已知相邻的偶数相差2,所以如果中间一个数是m,则比m大的数是(m+2),比m小的数是(m-2),如果这三个数的平均数是18,根据平均数的意义,列方程为m-2+m+m+2=18×3,然后解出方程,即可求出m的值,进而求出最小的数。
【详解】有三个连续的偶数,若中间一个数是m,那么比m大的数是(m+2),
m-2+m+m+2=18×3
解:m-2+m+m+2=54
3m=54
3m÷3=54÷3
m=18
18-2=16
如果这三个数的平均数是18,则最小的数是16。
【点睛】本题考查了用字母表示数以及根据列方程解决问题,明确相邻的偶数相差2。
11. 3 2.5
【分析】2支钢笔和3瓶墨水的钱数×3=6支钢笔和9瓶墨水的钱数,3支钢笔和5瓶墨水的钱数×2=6支钢笔和10瓶墨水的钱数,6支钢笔和10瓶墨水的钱数-6支钢笔和9瓶墨水的钱数=1瓶墨水的钱数,据此求出墨水钱数;单价×数量=总价,根据买2支钢笔和3瓶墨水共付13.5元,先求出3瓶墨水的钱数,13.5元-3瓶墨水的钱数=2支钢笔的钱数,2支钢笔的钱数÷2,即可求出一支钢笔的钱数。
【详解】墨水:(21.5×2-13.5×3)÷(5×2-3×3)
=(43-40.5)÷(10-9)
=2.5÷1
=2.5(元)
钢笔:(13.5-2.5×3)÷2
=(13.5-7.5)÷2
=6÷2
=3(元)
一支钢笔3元,一瓶墨水的单价是2.5元。
【点睛】关键是观察两个总钱数中钢笔和墨水的数量,灵活扩大一定的倍数,抵消掉一种物品的钱数,从而先求出一种物品的单价。
12. 1 9 8
【分析】观察统计图可知,找出小明多少小时做一次记录,以及一共记录几次;再用这天的最高气温减去最低气温,即可求出相差多少摄氏度,据此解答。
【详解】24-16=8(摄氏度)
小明对5月4日的气温进行了记录,并制成了统计图(如下图),从统计图中可以看出,他每隔1小时做一次记录,共进行了8次记录,从8:00-16:00,最高气温和最低气温相差8摄氏度。
【点睛】本题考查折线统计图的应用,并且利用统计图提供的信息解答问题。
13.×
【分析】含有未知数的等式叫做方程;据此解答。
【详解】4a=1是方程,4a+1不是方程。
故答案为:×
【点睛】本题主要考查方程的认识,解题时要明确方程必须具备两个条件:(1)必须是等式;(2)必须含有未知数。
14.×
【分析】分解质因数就是把一个合数写成几个质数连乘的形式。据此解答。
【详解】36=2×2×9,9是合数,不符合分解质因数的定义,故原题说法错误。
【点睛】本题主要考查分解质因数的方法。把一个合数写分解成几个质数连乘的形式是解答本题的关键。
15.√
【分析】除了1和它本身外,还含有其它因数的数是合数;据此解答即可。
【详解】在自然数中,1既不是质数,也不是合数,2、3、5都是质数,4是最小的合数。
故答案为:√
【点睛】掌握合数的含义,是解答此题的关键。
16.×
【分析】的分数单位是,的分数单位是。据此解答。
【详解】的分数单位是,的分数单位是,<,原题说法错误。
【点睛】本题考查了分数单位的认识及分子相同的分数大小的比较。
17.√
【分析】根据等式的性质,方程两边同时减4.8,再同时除以2,解方程即可。
【详解】2x+4.8=6.8
解:2x=6.8-4.8
2x=2
x=1
故答案为:√
【点睛】此题考查方程的解,也可把x=1代入方程,看方程两边是否相等。
18.最大公因数:1;14;13;
最小公倍数:90;42;39
【分析】求两个数的最大公因数、最小公倍数,如果两个数是互质数,那么它们的最大公因数是1、最小公倍数是这两个数的乘积;如果两个数是倍数关系,那么它们的最大公因数是较小的数、最小公倍数是较大的数;如果两个数是一般关系,可以利用分解质因数的方法,把两个数分别分解质因数,公有质因数的积就是最大公因数,公有质因数和各自独有质因数的连乘积就是最小公倍数;据此解答。
【详解】(1)10和9互质,所以10和9的最大公因数是1,最小公倍数是10×9=90;
(2)14和42成倍数关系,所以14个42的最大公因数是14,最小公倍数是42;
(3)13和39成倍数关系,所以13个39的最大公因数是13,最小公倍数是39。
19.x=3.8;x=25;x=1.8
【分析】5x-8.3=10.7,根据等式的性质1,方程两边同时加上8.3,再根据等式的性质2,方程两边同时除以5即可;
2.7x+3.1x=145,先化简方程左边含义x的算式,即求出2.7+3.1的和,再根据等式的性质2,方程两边同时除以2.7+3.1的和即可;
7x+0.4×5=14.6,先计算出0.4×5的积,再根据等式的性质1,方程两边同时减去0.4×5的积,再根据等式的性质2,方程两边同时除以7即可。
【详解】5x-8.3=10.7
解:5x-8.3+8.3=10.7+8.3
5x=19
5x÷5=19÷5
x=3.8
2.7x+3.1=145
解:5.8x=145
5.8x÷5.8=145÷5.8
x=25
7x+0.4×5=14.6
解:7x+2=14.6
7x+2-2=14.6-2
7x=12.6
7x÷7=12.6÷7
x=1.8
20.5x-x=280
x=70
【分析】根据图意可知,梨有x千克,苹果是梨的5倍,即5x,已知苹果比梨多280千克,得数量关系式:苹果-梨=280,根据数量关系列方程解答。
【详解】解:设梨有x千克
5x-x=280
4x=280
4x÷4=280÷4
x=280÷4
x=70
梨有70千克。
21.小东是第一名,小杰是第2名,小军是第三名。
【分析】先依据小数、分数大小的比较方法,把分数化成小数再比较出三个数的大小,据此即可得解。
【详解】因为11.1,0.95
1.15米>1.1米>0.95米
答:他们的成绩排名依次是:小东是第一名,小杰是第2名,小军是第三名。
【点睛】此题主要考查小数大小的比较方法在实际生活中的应用。
22.9厘米;20块
【分析】由题意可知:小正方形的边长既是长45厘米的因数,也是宽36厘米的因数,且不能有剩余。即为求45和36的最大公因数,据此解答。
【详解】45=3×3×5
36=2×2×3×3
45和36的最大公因数是:3×3=9
即小正方形的边长最大是9厘米。
45×36÷(9×9)
=1620÷81
=20(块)
答:剪成的小正方形的边长最大是9厘米,共能剪成20块。
【点睛】本题考察了求解两数最大公因数的方法。可用分解质因数求解,也可用短除法求出两数的最大公因数。
23.20分钟;7时40分
【分析】先求至少要经过多少分钟又同时发车,即求4和5的最小公倍数;根据求两个数的最小公倍数的方法:即这两个数的公有质因数与独有质因数的连乘积;然后再求出此时的时刻,据此解答即可。
【详解】4和5的最小公倍数为:4×5=20,即20分钟。
7时20分+20分钟=7时40分。
答:至少再过20分钟两车第二次同时发车,是7时40分。
【点睛】此题主要考查求两个数的最小公倍数的方法:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;数字大的可以用短除解答。
24.75千米
【分析】根据速度和×相遇时间=路程和,设汽车每小时行驶x千米,据此列方程为(45+x)×3=360,然后解出方程即可。
【详解】解:设汽车每小时行驶x千米。
(45+x)×3=360
(45+x)×3÷3=360÷3
45+x=120
45+x-45=120-45
x=75
答:汽车每小时行驶75千米。
【点睛】本题考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
25.266米
【分析】根据题意可知,徐州苏宁广场主塔楼的高度×2-64米=上海东方明珠广播电视塔的高度,设徐州苏宁广场主塔楼高x米,列方程为2x-64=468,然后解出方程即可。
【详解】解:设徐州苏宁广场主塔楼高x米。
2x-64=468
2x-64+64=468+64
2x=532
2x÷2=532÷2
x=266
答:徐州苏宁广场主塔楼高266米。
【点睛】本题主要考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
26.(1)见详解
(2)500台
(3)28.5万元
【分析】(1)根据统计表所提供的数据,在统计图中描出空调和冰箱销售量的点,顺次连接,标上数据等即可完成折线统计图;
(2)首先求出2022年下半年一共销售空调多少台;然后用它除以6,求出平均每月销售空调多少台即可;
(3)首先求出2022年第三季度一共销售冰箱多少台;然后用它乘每台冰箱获利的钱数即可。
【详解】(1)
(2)(450+750+550+350+300+600)÷6
=(1200+550+350+300+600)÷6
=(1750+350+300+600)÷6
=(2100+300+600)÷6
=(2400+600)÷6
=3000÷6
=500(台)
答:商场下半年平均每月销售空调500台。
(3)(300+500+350+300+250+200)×150
=(800+350+300+250+200)×150
=(1150+300+250+200)×150
=(1450+250+200)×150
=(1700+200)×150
=1900×150
=285000(元)
285000元=28.5万元
答:这个商场2022年第三季度冰箱共获利28.5万元。
【点睛】本题考查统计图的制作,根据观察统计图并从图中获取信息,再解答问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中经典题型检测卷2023-2024学年数学五年级下册苏教版
一、选择题
1.折线统计图的特点是( )。
A.表示数量的多少 B.表示数量的增减变化
C.既表示数量的多少又表示数量的增减变化 D.以上答案都不正确
2.35÷□=4……3,如果商用分数表示是( )。
A. B. C. D.
3.汾河湿地公园的一段水域上生活有野鸭114只,比白鹭数量的3倍少30只。设白鹭的数量是x只,下列方程错误的是( )。
A.3x-30=114 B.114-3x=30 C.3x-114=30 D.3x=114+30
4.用1、2、3这三个数字组成的三位数一定是( )的倍数。
A.2 B.3 C.2或3 D.4
5.两堆黄沙一样重,第一堆运走吨,第二堆运走了它的,运走的黄沙相比( )。
A.第一堆多 B.第二堆多 C.一样多 D.无法确定
6.一根1米长的绳子,连续对折4次,每段长( )米。
A. B. C. D.
二、填空题
7.7厘米=分米 17千克=吨 73分=小时
8.一个两位数3,它既有因数2,又是3的倍数,里的能填的数最大是( ),把这个两位数分解质因数是( )。
9.( )统计图不仅能够表示出数量的多少,还能反映数量的增减变化情况。
10.有三个连续的偶数,若中间一个数是m,那么比m大的数是( );如果这三个数的平均数是18,则最小的数是( )。
11.买2支钢笔和3瓶墨水共付13.5元,买同样的3支钢笔和5瓶墨水共付21.5元。一支钢笔( )元,一瓶墨水的单价是( )元。
12.小明对5月4日的气温进行了记录,并制成了统计图(如下图),从统计图中可以看出,他每隔( )小时做一次记录,共进行了( )次记录,从8:00-16:00,最高气温和最低气温相差( )摄氏度。
三、判断题
13.4a=1和4a+1都是方程。( )
14.将36分解质因数为:36=2×2×9。( )
15.最小的合数是4。( )
16.的分数单位比的分数单位大。( )
17.x=1是方程2x+4.8=6.8的解。( )
四、计算题
18.下面各组数的最大公因数和最小公倍数。
(1)10和9 (2)14和42 (3)13和39
19.解方程。
5x-8.3=10.7 2.7x+3.1x=145 7x+0.4×5=14.6
20.看图列方程并解答。
五、解答题
21.在一次跳高比赛中,小杰跳了1米,小东跳了1.15米,小军跳了米,请你给他们排个名次?
22.一个长方形长45厘米,宽36厘米,把它剪成相等的小正方形,不能有剩余,剪成的小正方形的边长最大是多少厘米?共能剪成多少块?
23.两路公交车,甲车每4分钟发一班,乙车每5分钟发一班,它们从7:20第一次同时发车后,至少再过多少分钟两车第二次同时发车?是几时几分?
24.甲、乙两城相距360千米,一辆汽车从甲城开往乙城,一辆摩托车同时从乙城开往甲城。摩托车每小时行驶45千米,3小时后两车相遇。汽车每小时行驶多少千米?(列方程解答)
25.上海东方明珠广播电视塔高468米,比号称“徐州之巅”的徐州苏宁广场主塔楼高的2倍少64米,徐州苏宁广场主塔楼高多少米?(用方程解答)
26.新时代商场2022年下半年空调和冰箱的销售情况如表所示:
月份 销量 商品 7 8 9 10 11 12
空调 450 750 550 350 300 600
冰箱 300 500 350 300 250 200
(1)根据上表中的数据制成折线统计图。
(2)商场下半年平均每月销售空调多少台?
(3)如果每台冰箱的利润是150元,那么这个商场2022年第三季度冰箱共获利多少万元?
参考答案:
1.C
【分析】折线统计图可以表示数量的增减变化;条形统计图可以表示数量的多少。
【详解】根据分析可知,折线统计图的特点是表示数量的增减变化。
【点睛】考查折线统计图的特点是表示数量的增减变化。
2.B
【分析】根据除数=(被除数-余数)÷商,求出□中的除数,再根据除法与分数的关系计算出商,据此解答。
【详解】(35-3)÷4
=32÷4
=8
35÷8=
35÷□=4……3,如果商用分数表示是。
故答案为:B
【点睛】本题考查被除数、除数、商和余数之间的关系,以及除法与分数的关系。
3.B
【分析】设白鹭的数量是x只,野鸭的数量比白鹭的3倍少30只,即白鹭的只数×3-30=野鸭的只数,野鸭只数有114只,列方程:3x-30=114,据此分析,进行解答。
【详解】设白鹭的数量是x只。则:
3x-30=114
3x-114=30
3x=114+30
汾河湿地公园的一段水域上生活有野鸭114只,比白鹭数量的3倍少30只。设白鹭的数量是x只,下列方程错误的是114-3x=30。
故答案为:B
【点睛】解答本题的关键是根据题意,找清楚野鸭和白鹭数量之间的关系,进而解答。
4.B
【分析】先写出1、2、3可以组成的三位数,再根据2、3、5的倍数特征进行判断;
2的倍数特征:个位上是0、2、4、6、8的数;
5的倍数特征:个位上是0或5的数;
3的倍数特征:各个数位之和能够被3整数。
【详解】1、2、3组成的三位数有123、132、213、231、321、312;
1、2、3组成的三位数都不是5的倍数;
123、213、231、321都不是2的倍数,也不是4的倍数;
1+2+3=6,6能被3整除,是3的倍数;组成的三位数一定是3的倍数。
用1、2、3这三个数字组成的三位数一定是3的倍数。
故答案为:B
【点睛】熟练掌握2、3、5的倍数特征是解答本题的关键。
5.D
【分析】如果这两堆黄沙都是1吨,1吨的就是吨,两堆运走的一样重,剩下的也一样重;如果这两堆黄沙都不足1吨,不足1吨的就小于吨,第一堆运走的重;如果这两堆黄沙都大于1吨,大于1吨的就大于吨,第二堆运走的重;据此可解。
【详解】当这两堆黄沙都是1吨,1×=,吨=吨,两堆运走的一样重;
当这两堆黄沙都不足1吨,假设为0.3吨时,0.3×=0.1,0.1吨<吨,因此第一堆运走的重;
当这两堆黄沙都大于1吨,假设为3吨时,3×=1,1吨>吨,因此第二堆运走的重;
这两堆黄沙的质量不确定,剩下的黄沙重量相比较,无法确定哪堆重。
故答案为:D
【点睛】第一堆运走的吨是一个具体的量,而第二堆运走的是一个分率,只有在确定了这堆黄沙质量的情况下才能确定它的质量,因此,在不确定黄沙质量的情况下,无法确定它的质量。
6.D
【分析】第一次对折后,就是把绳子平均分成2份,第二次对折后,就是把绳子平均分成 4份,第三次对折后,就是把绳子平均分成8份,第四次对折后,就是把绳子平均分成16分,求每段长,用绳子的长度1÷16解答。
【详解】根据分析可知,对折4次,把绳子平均分成16份。
1÷16=(米)
一根1米长的绳子,连续对折4次,每段长米。
故答案为:D
【点睛】解答本题的关键是明确对折4次就是把绳子平均分成16份。
7.;;
【分析】根据1分米=10厘米,1吨=1000千克,1小时=60分钟,高级单位化低级单位要乘进率,低级单位化高级单位要除以进率,据此解答。
【详解】7厘米=分米
17千克=吨
73分=小时
【点睛】本题考查了长度单位、质量单位、时间单位的换算,明确高级单位化低级单位要乘进率,低级单位化高级单位要除以进率。
8. 6 36=2×2×3×3
【分析】根据2、3的倍数的特征:个位数是0、2、4、6、8是都是2的倍数;一个数各数位上的数字之和是3的倍数,这个数一定是3的倍数。因此,既有因数2,又是3的倍数,里的能填的数最大是6,再把36分解质因数即可。
【详解】一个两位数3,它既有因数2,又是3的倍数,里的能填的数最大是(6),把这个两位数分解质因数是(36=2×2×3×3)。
【点睛】掌握能被2、3整除的数的特征是解答此题的关键。
9.折线
【详解】折线统计图不仅能够表示出数量的多少,还能反映数量的增减变化情况。例如:
折线统计图不仅表示1年内每个月的平均温度,也可以看出每个月温度的变化。
10. 2+m/ m+2 16
【分析】已知相邻的偶数相差2,所以如果中间一个数是m,则比m大的数是(m+2),比m小的数是(m-2),如果这三个数的平均数是18,根据平均数的意义,列方程为m-2+m+m+2=18×3,然后解出方程,即可求出m的值,进而求出最小的数。
【详解】有三个连续的偶数,若中间一个数是m,那么比m大的数是(m+2),
m-2+m+m+2=18×3
解:m-2+m+m+2=54
3m=54
3m÷3=54÷3
m=18
18-2=16
如果这三个数的平均数是18,则最小的数是16。
【点睛】本题考查了用字母表示数以及根据列方程解决问题,明确相邻的偶数相差2。
11. 3 2.5
【分析】2支钢笔和3瓶墨水的钱数×3=6支钢笔和9瓶墨水的钱数,3支钢笔和5瓶墨水的钱数×2=6支钢笔和10瓶墨水的钱数,6支钢笔和10瓶墨水的钱数-6支钢笔和9瓶墨水的钱数=1瓶墨水的钱数,据此求出墨水钱数;单价×数量=总价,根据买2支钢笔和3瓶墨水共付13.5元,先求出3瓶墨水的钱数,13.5元-3瓶墨水的钱数=2支钢笔的钱数,2支钢笔的钱数÷2,即可求出一支钢笔的钱数。
【详解】墨水:(21.5×2-13.5×3)÷(5×2-3×3)
=(43-40.5)÷(10-9)
=2.5÷1
=2.5(元)
钢笔:(13.5-2.5×3)÷2
=(13.5-7.5)÷2
=6÷2
=3(元)
一支钢笔3元,一瓶墨水的单价是2.5元。
【点睛】关键是观察两个总钱数中钢笔和墨水的数量,灵活扩大一定的倍数,抵消掉一种物品的钱数,从而先求出一种物品的单价。
12. 1 9 8
【分析】观察统计图可知,找出小明多少小时做一次记录,以及一共记录几次;再用这天的最高气温减去最低气温,即可求出相差多少摄氏度,据此解答。
【详解】24-16=8(摄氏度)
小明对5月4日的气温进行了记录,并制成了统计图(如下图),从统计图中可以看出,他每隔1小时做一次记录,共进行了8次记录,从8:00-16:00,最高气温和最低气温相差8摄氏度。
【点睛】本题考查折线统计图的应用,并且利用统计图提供的信息解答问题。
13.×
【分析】含有未知数的等式叫做方程;据此解答。
【详解】4a=1是方程,4a+1不是方程。
故答案为:×
【点睛】本题主要考查方程的认识,解题时要明确方程必须具备两个条件:(1)必须是等式;(2)必须含有未知数。
14.×
【分析】分解质因数就是把一个合数写成几个质数连乘的形式。据此解答。
【详解】36=2×2×9,9是合数,不符合分解质因数的定义,故原题说法错误。
【点睛】本题主要考查分解质因数的方法。把一个合数写分解成几个质数连乘的形式是解答本题的关键。
15.√
【分析】除了1和它本身外,还含有其它因数的数是合数;据此解答即可。
【详解】在自然数中,1既不是质数,也不是合数,2、3、5都是质数,4是最小的合数。
故答案为:√
【点睛】掌握合数的含义,是解答此题的关键。
16.×
【分析】的分数单位是,的分数单位是。据此解答。
【详解】的分数单位是,的分数单位是,<,原题说法错误。
【点睛】本题考查了分数单位的认识及分子相同的分数大小的比较。
17.√
【分析】根据等式的性质,方程两边同时减4.8,再同时除以2,解方程即可。
【详解】2x+4.8=6.8
解:2x=6.8-4.8
2x=2
x=1
故答案为:√
【点睛】此题考查方程的解,也可把x=1代入方程,看方程两边是否相等。
18.最大公因数:1;14;13;
最小公倍数:90;42;39
【分析】求两个数的最大公因数、最小公倍数,如果两个数是互质数,那么它们的最大公因数是1、最小公倍数是这两个数的乘积;如果两个数是倍数关系,那么它们的最大公因数是较小的数、最小公倍数是较大的数;如果两个数是一般关系,可以利用分解质因数的方法,把两个数分别分解质因数,公有质因数的积就是最大公因数,公有质因数和各自独有质因数的连乘积就是最小公倍数;据此解答。
【详解】(1)10和9互质,所以10和9的最大公因数是1,最小公倍数是10×9=90;
(2)14和42成倍数关系,所以14个42的最大公因数是14,最小公倍数是42;
(3)13和39成倍数关系,所以13个39的最大公因数是13,最小公倍数是39。
19.x=3.8;x=25;x=1.8
【分析】5x-8.3=10.7,根据等式的性质1,方程两边同时加上8.3,再根据等式的性质2,方程两边同时除以5即可;
2.7x+3.1x=145,先化简方程左边含义x的算式,即求出2.7+3.1的和,再根据等式的性质2,方程两边同时除以2.7+3.1的和即可;
7x+0.4×5=14.6,先计算出0.4×5的积,再根据等式的性质1,方程两边同时减去0.4×5的积,再根据等式的性质2,方程两边同时除以7即可。
【详解】5x-8.3=10.7
解:5x-8.3+8.3=10.7+8.3
5x=19
5x÷5=19÷5
x=3.8
2.7x+3.1=145
解:5.8x=145
5.8x÷5.8=145÷5.8
x=25
7x+0.4×5=14.6
解:7x+2=14.6
7x+2-2=14.6-2
7x=12.6
7x÷7=12.6÷7
x=1.8
20.5x-x=280
x=70
【分析】根据图意可知,梨有x千克,苹果是梨的5倍,即5x,已知苹果比梨多280千克,得数量关系式:苹果-梨=280,根据数量关系列方程解答。
【详解】解:设梨有x千克
5x-x=280
4x=280
4x÷4=280÷4
x=280÷4
x=70
梨有70千克。
21.小东是第一名,小杰是第2名,小军是第三名。
【分析】先依据小数、分数大小的比较方法,把分数化成小数再比较出三个数的大小,据此即可得解。
【详解】因为11.1,0.95
1.15米>1.1米>0.95米
答:他们的成绩排名依次是:小东是第一名,小杰是第2名,小军是第三名。
【点睛】此题主要考查小数大小的比较方法在实际生活中的应用。
22.9厘米;20块
【分析】由题意可知:小正方形的边长既是长45厘米的因数,也是宽36厘米的因数,且不能有剩余。即为求45和36的最大公因数,据此解答。
【详解】45=3×3×5
36=2×2×3×3
45和36的最大公因数是:3×3=9
即小正方形的边长最大是9厘米。
45×36÷(9×9)
=1620÷81
=20(块)
答:剪成的小正方形的边长最大是9厘米,共能剪成20块。
【点睛】本题考察了求解两数最大公因数的方法。可用分解质因数求解,也可用短除法求出两数的最大公因数。
23.20分钟;7时40分
【分析】先求至少要经过多少分钟又同时发车,即求4和5的最小公倍数;根据求两个数的最小公倍数的方法:即这两个数的公有质因数与独有质因数的连乘积;然后再求出此时的时刻,据此解答即可。
【详解】4和5的最小公倍数为:4×5=20,即20分钟。
7时20分+20分钟=7时40分。
答:至少再过20分钟两车第二次同时发车,是7时40分。
【点睛】此题主要考查求两个数的最小公倍数的方法:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;数字大的可以用短除解答。
24.75千米
【分析】根据速度和×相遇时间=路程和,设汽车每小时行驶x千米,据此列方程为(45+x)×3=360,然后解出方程即可。
【详解】解:设汽车每小时行驶x千米。
(45+x)×3=360
(45+x)×3÷3=360÷3
45+x=120
45+x-45=120-45
x=75
答:汽车每小时行驶75千米。
【点睛】本题考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
25.266米
【分析】根据题意可知,徐州苏宁广场主塔楼的高度×2-64米=上海东方明珠广播电视塔的高度,设徐州苏宁广场主塔楼高x米,列方程为2x-64=468,然后解出方程即可。
【详解】解:设徐州苏宁广场主塔楼高x米。
2x-64=468
2x-64+64=468+64
2x=532
2x÷2=532÷2
x=266
答:徐州苏宁广场主塔楼高266米。
【点睛】本题主要考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
26.(1)见详解
(2)500台
(3)28.5万元
【分析】(1)根据统计表所提供的数据,在统计图中描出空调和冰箱销售量的点,顺次连接,标上数据等即可完成折线统计图;
(2)首先求出2022年下半年一共销售空调多少台;然后用它除以6,求出平均每月销售空调多少台即可;
(3)首先求出2022年第三季度一共销售冰箱多少台;然后用它乘每台冰箱获利的钱数即可。
【详解】(1)
(2)(450+750+550+350+300+600)÷6
=(1200+550+350+300+600)÷6
=(1750+350+300+600)÷6
=(2100+300+600)÷6
=(2400+600)÷6
=3000÷6
=500(台)
答:商场下半年平均每月销售空调500台。
(3)(300+500+350+300+250+200)×150
=(800+350+300+250+200)×150
=(1150+300+250+200)×150
=(1450+250+200)×150
=(1700+200)×150
=1900×150
=285000(元)
285000元=28.5万元
答:这个商场2022年第三季度冰箱共获利28.5万元。
【点睛】本题考查统计图的制作,根据观察统计图并从图中获取信息,再解答问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
