2.2法拉第电磁感应定律 课件(共32张ppt)物理人教版(2019)选择性必修第二册
文档属性
| 名称 | 2.2法拉第电磁感应定律 课件(共32张ppt)物理人教版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-19 19:25:14 | ||
图片预览






文档简介
(共32张PPT)
第2节 法拉第电磁感应定律
人教版(2019)选择性必修二
第二章 电磁感应
人教版(2019)选择性必修二
2024
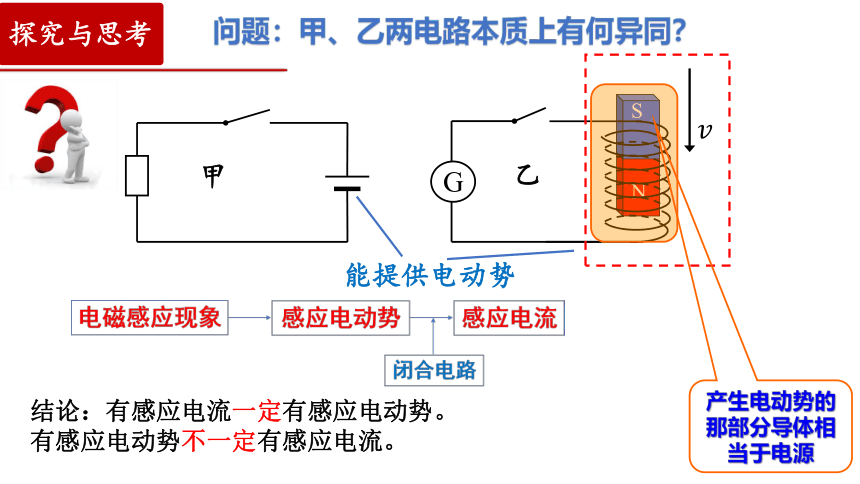
问题:甲、乙两电路本质上有何异同?
甲
N
S
G
乙
能提供电动势
结论:有感应电流一定有感应电动势。
有感应电动势不一定有感应电流。
探究与思考
产生电动势的那部分导体相当于电源
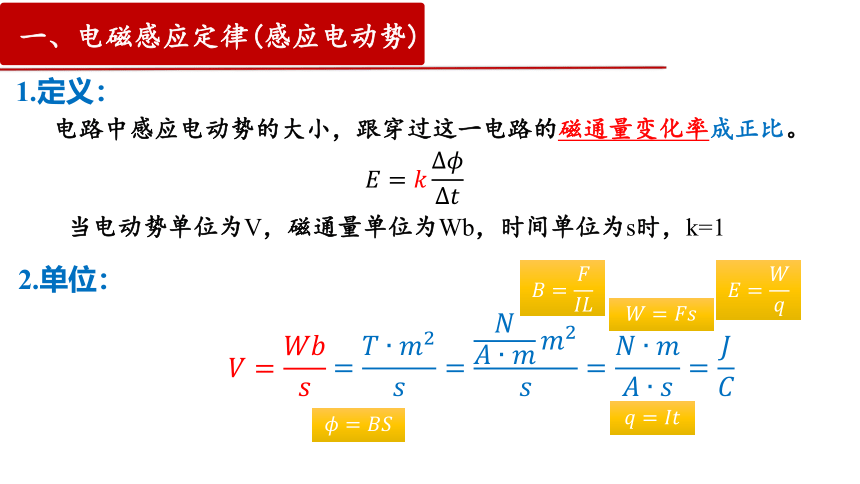
电路中感应电动势的大小,跟穿过这一电路的磁通量变化率成正比。
1.定义:
当电动势单位为V,磁通量单位为Wb,时间单位为s时,k=1
2.单位:
一、电磁感应定律(感应电动势)
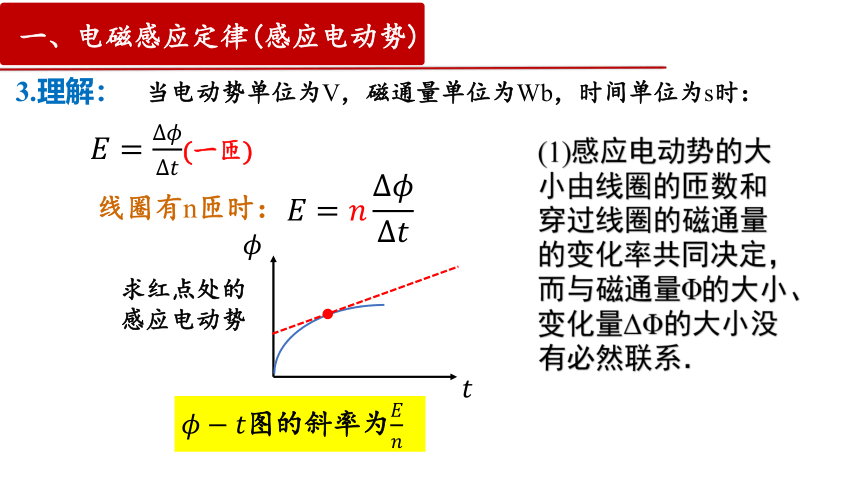
当电动势单位为V,磁通量单位为Wb,时间单位为s时:
(一匝)
线圈有n匝时:
求红点处的
感应电动势
图的斜率为
一、电磁感应定律(感应电动势)
(1)感应电动势的大小由线圈的匝数和穿过线圈的磁通量的变化率共同决定,而与磁通量Φ的大小、变化量ΔΦ的大小没有必然联系.
3.理解:
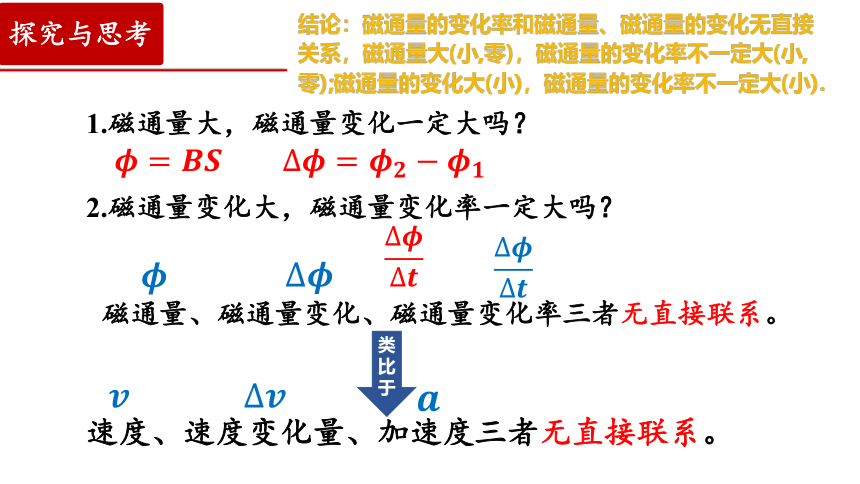
1.磁通量大,磁通量变化一定大吗?
2.磁通量变化大,磁通量变化率一定大吗?
磁通量、磁通量变化、磁通量变化率三者无直接联系。
速度、速度变化量、加速度三者无直接联系。
探究与思考
结论:磁通量的变化率和磁通量、磁通量的变化无直接关系,磁通量大(小,零),磁通量的变化率不一定大(小,零);磁通量的变化大(小),磁通量的变化率不一定大(小).
类比于
3.导体棒的运动速度越大,产生的感应电动势越大吗
提示:导体棒切割磁感线时,产生的感应电动势的大小与垂直磁感线的速度有关,而速度大,垂直磁感线方向的速度不一定大。所以,导体棒运动速度越大,产生的感应电动势不一定越大。
4.Φ、ΔΦ、 与线圈匝数有关吗 感应电动势E与线圈匝数有关吗
提示:Φ、ΔΦ、 均与某一面积相联系,与线圈匝数无关;n匝线圈相当于n个单匝线圈的串联,所以感应电动势E与线圈匝数有关。
探究与思考
(1)磁通量的变化是由面积变化引起时,ΔΦ=B·ΔS,则
(2)磁通量的变化是由磁场变化引起时,ΔΦ=ΔB·S,则
(3)磁通量的变化是由面积和磁场变化共同引起时,
则根据定义求,ΔΦ=Φ末-Φ初
应用法拉第电磁感应定律的三种情况
、、的比较
物理意义 与电磁感应
关系
磁通量
磁通量变化
磁通量变化率
穿过回路的磁感线条数
穿过回路的磁通量变化
穿过回路的磁通量变化
的快慢
无直接关系
产生感应
电动势条件
决定感应
电动势大小
探究与思考
1.感应电动势E的大小取决于穿过电路的磁通量的变化率,而与Φ的大小、ΔΦ的大小没有必然的关系,与电路的电阻R无关;感应电流的大小与E和回路总电阻R有关。
2.磁通量的变化率,是Φ-t图像上某点切线的斜率,可反映单匝线圈感应电动势的大小和方向。
3.E=n只表示感应电动势的大小,不涉及其正负,计算时ΔΦ应取绝对值,至于感应电流的方向,可以用楞次定律去判定。
4.计算电动势时,常有以下两种情况:
E=n·S——面积不变,磁感应强度变化;E=n·B——面积改变,磁感应强度不变。
归纳与总结
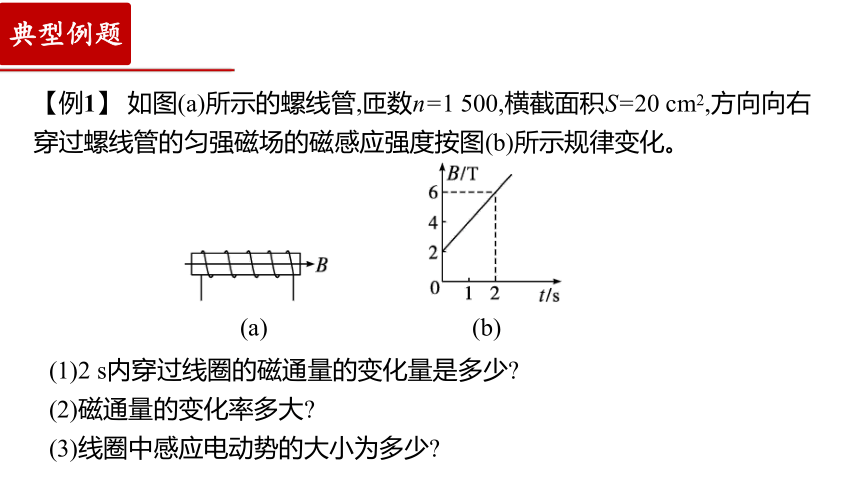
【例1】 如图(a)所示的螺线管,匝数n=1 500,横截面积S=20 cm2,方向向右穿过螺线管的匀强磁场的磁感应强度按图(b)所示规律变化。
(a)
(b)
典型例题
(1)2 s内穿过线圈的磁通量的变化量是多少
(2)磁通量的变化率多大
(3)线圈中感应电动势的大小为多少
【答案】(1)8×10-3 Wb (2)4×10-3 Wb/s (3)6 V
(a)
(b)
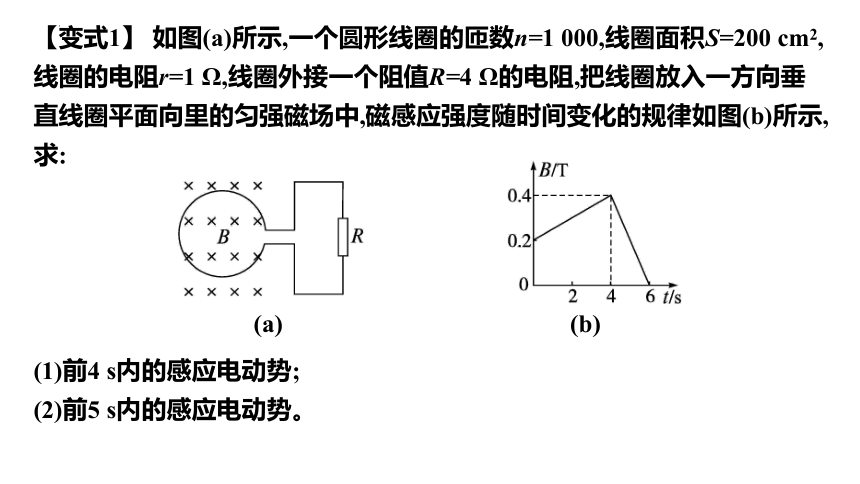
【变式1】 如图(a)所示,一个圆形线圈的匝数n=1 000,线圈面积S=200 cm2,线圈的电阻r=1 Ω,线圈外接一个阻值R=4 Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化的规律如图(b)所示,求:
(1)前4 s内的感应电动势;
(2)前5 s内的感应电动势。
【答案】(1)1 V (2)0
思考:如图所示,闭合电路一部分导体ab处于匀强磁场中,磁感应强度为B,ab的长度为L,ab以速度v匀速垂直切割磁感线,试利用法拉第电磁感应定律求回路中产生的感应电动势。
探究与思考
1.导体垂直切割磁感线:
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
a
b
v
a
b
匀强磁场的磁感应强度为,长为的导体棒以速度匀速切割磁感线。求产生的感应电动势。
即
二、导体切割磁感线时的感应电动势
动生电动势:由于导体运动而产生的电动势。
θ
v
B
2.导体斜切磁感线与夹角:
二、导体切割磁感线时的感应电动势
注意:1.为切割磁感线的有效长度。
(垂直于、的两端口距离)
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
v
v
v
× × × ×
× × × ×
× × × ×
× × × ×
v
2. 是的特例,只适用于切割。
3. 为瞬时速度时, 为瞬时感应电动势;
为平均速度时, 为平均感应电动势。
二、导体切割磁感线时的感应电动势
公式E=n 与E=BLvsin α的区别与联系
项目 E=n E=BLvsin α
区别 研究 对象 某个回路 回路中做切割磁感线运动的那部分导体
研究 内容 (1)求的是Δt时间内的平均感应电动势,E与某段时间或某个过程对应 (2)当Δt→0时,E为瞬时感应电动势 (1)若v为瞬时速度,求的是瞬时感应电动势
(2)若v为平均速度,求的是平均感应电动势
(3)当B、L、v三者均不变时,平均感应电动势与瞬时感应电动势相等
适用 范围 对任何电路普遍适用 只适用于导体切割磁感线运动的情况
归纳与总结
联系 (1)E=BLvsin α是由E=n在一定条件下推导出来的
(2)整个回路的感应电动势为零时,回路中某段导体的感应电动势不一定为零
计算感应电动势的方法:
感应电动势
瞬时感应电动势
平均感应电动势
为瞬时速度
为平均速度
功率
瞬时功率
平均功率
为瞬时速度
为平均速度
归纳总结
【例2】如图所示,平行导轨间距为d,其左端接一个电阻R,匀强磁场的磁感应强度为B,方向垂直于平行金属导轨所在平面,一根金属棒与导轨成θ角放置,金属棒与导轨的电阻均不计。当金属棒沿垂直于棒的方向以恒定的速度v在导轨上滑行时,通过电阻R的电流大小是( )
D
典型例题
如图所示,导体棒长为L,磁感应强度为B,方向垂直于纸面向里。
1.以O为圆心转动,角速度为。
判断O、A电势高低;
求感应电动势。
× × × ×
× × × ×
× × × ×
× × × ×
O
L
A
三、导体转动切割磁感线
× × ×
× × ×
× × ×
× × ×
× × ×
× × ×
B
A
O
●
B
A
O
●
2.AO=BO=L。
3.AO=L,BO=。
三、导体转动切割磁感线
4.AB=L,BO=。
导体棒延长至O点,
则AO段有
× × ×
× × ×
× × ×
B
A
O
●
●
法一:补偿法。
BO段有
三、导体转动切割磁感线
4.AB=L,BO=。
A点速度
× × ×
× × ×
× × ×
B
A
O
●
●
法二:求棒上的平均速度。
B点速度
平均速度
●
棒中点速度
●
●
三、导体转动切割磁感线
本课总结
1.关于电磁感应,下述说法中正确的是( )
A.穿过线圈的磁通量越大,感应电动势越大
B.穿过线圈的磁通量为零,感应电动势一定为零
C.穿过线圈的磁通量的变化越大,感应电动势越大
D.穿过线圈的磁通量变化越快,感应电动势越大
D
注意:感应电动势E与Φ、△Φ、 △Φ/△t的关系
Φ/10-2Wb
t/s
A
B
D
0
1
2
0.1
2.单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场。若线圈所围面积里磁通量随时间变化的规律如图所示,则( )
A.线圈中0时刻感应电动势最大 B.线圈中D时刻感应电动势为零 C.线圈中D时刻感应电动势最大 D.线圈中0到D时间内平均感应电动势为0.4V
ABD
斜率表示Φ的变化率
3.(公式E=n 的应用)穿过一个单匝闭合线圈的磁通量始终为每秒均匀增加2 Wb,则( )
A.线圈中感应电动势每秒增加2 V
B.线圈中感应电动势每秒减少2 V
C.线圈中感应电动势始终为2 V
D.线圈中感应电动势始终为一个确定值,但由于线圈有电阻,电动势小于2 V
C
4.(公式E=BLv的应用)如图所示,一金属弯杆处在磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,已知ab=bc=L,当它以速度v向右平动时,a、c两点间的电势差大小为( )
A.BLv
B.BLvsin θ
C.BLvcos θ
D.BLv(1+sin θ)
B
解析:杆切割磁感线的有效长度为Lsin θ,故B正确。
5.如图所示,半径为r的金属圆盘在垂直于盘面的匀强磁场B中,绕O轴以角速度ω沿逆时针方向匀速转动,则通过电阻R的电流的方向和大小是(金属圆盘的电阻不计)( )
A.由c到d,;
B.由d到c,;
C.由c到d,;
D.由d到c,。
D
6.如图所示,线框用裸导线组成,cd、ef两边所在平面与磁感线相互垂直且cd、ef 相互平行,导体棒ab水平放置并可沿cd、ef无摩擦滑动,而导体棒ab所在处的匀强磁场B2=2 T,已知ab长l=0.1 m,整个电路总电阻R=5 Ω。螺线管匝数n=4,螺线管横截面积S=0.1 m2。在螺线管内有图示方向的磁场B1,若=10 T/s恒定不变时,导体棒恰好处于静止状态,求:(g取10 m/s2)
(1)通过导体棒ab的电流大小;
(2)导体棒ab的质量m。
答案:(1)0.8 A (2)0.016 kg
(1)通过导体棒ab的电流大小;
(2)导体棒ab的质量m。
第2节 法拉第电磁感应定律
人教版(2019)选择性必修二
第二章 电磁感应
人教版(2019)选择性必修二
2024
问题:甲、乙两电路本质上有何异同?
甲
N
S
G
乙
能提供电动势
结论:有感应电流一定有感应电动势。
有感应电动势不一定有感应电流。
探究与思考
产生电动势的那部分导体相当于电源
电路中感应电动势的大小,跟穿过这一电路的磁通量变化率成正比。
1.定义:
当电动势单位为V,磁通量单位为Wb,时间单位为s时,k=1
2.单位:
一、电磁感应定律(感应电动势)
当电动势单位为V,磁通量单位为Wb,时间单位为s时:
(一匝)
线圈有n匝时:
求红点处的
感应电动势
图的斜率为
一、电磁感应定律(感应电动势)
(1)感应电动势的大小由线圈的匝数和穿过线圈的磁通量的变化率共同决定,而与磁通量Φ的大小、变化量ΔΦ的大小没有必然联系.
3.理解:
1.磁通量大,磁通量变化一定大吗?
2.磁通量变化大,磁通量变化率一定大吗?
磁通量、磁通量变化、磁通量变化率三者无直接联系。
速度、速度变化量、加速度三者无直接联系。
探究与思考
结论:磁通量的变化率和磁通量、磁通量的变化无直接关系,磁通量大(小,零),磁通量的变化率不一定大(小,零);磁通量的变化大(小),磁通量的变化率不一定大(小).
类比于
3.导体棒的运动速度越大,产生的感应电动势越大吗
提示:导体棒切割磁感线时,产生的感应电动势的大小与垂直磁感线的速度有关,而速度大,垂直磁感线方向的速度不一定大。所以,导体棒运动速度越大,产生的感应电动势不一定越大。
4.Φ、ΔΦ、 与线圈匝数有关吗 感应电动势E与线圈匝数有关吗
提示:Φ、ΔΦ、 均与某一面积相联系,与线圈匝数无关;n匝线圈相当于n个单匝线圈的串联,所以感应电动势E与线圈匝数有关。
探究与思考
(1)磁通量的变化是由面积变化引起时,ΔΦ=B·ΔS,则
(2)磁通量的变化是由磁场变化引起时,ΔΦ=ΔB·S,则
(3)磁通量的变化是由面积和磁场变化共同引起时,
则根据定义求,ΔΦ=Φ末-Φ初
应用法拉第电磁感应定律的三种情况
、、的比较
物理意义 与电磁感应
关系
磁通量
磁通量变化
磁通量变化率
穿过回路的磁感线条数
穿过回路的磁通量变化
穿过回路的磁通量变化
的快慢
无直接关系
产生感应
电动势条件
决定感应
电动势大小
探究与思考
1.感应电动势E的大小取决于穿过电路的磁通量的变化率,而与Φ的大小、ΔΦ的大小没有必然的关系,与电路的电阻R无关;感应电流的大小与E和回路总电阻R有关。
2.磁通量的变化率,是Φ-t图像上某点切线的斜率,可反映单匝线圈感应电动势的大小和方向。
3.E=n只表示感应电动势的大小,不涉及其正负,计算时ΔΦ应取绝对值,至于感应电流的方向,可以用楞次定律去判定。
4.计算电动势时,常有以下两种情况:
E=n·S——面积不变,磁感应强度变化;E=n·B——面积改变,磁感应强度不变。
归纳与总结
【例1】 如图(a)所示的螺线管,匝数n=1 500,横截面积S=20 cm2,方向向右穿过螺线管的匀强磁场的磁感应强度按图(b)所示规律变化。
(a)
(b)
典型例题
(1)2 s内穿过线圈的磁通量的变化量是多少
(2)磁通量的变化率多大
(3)线圈中感应电动势的大小为多少
【答案】(1)8×10-3 Wb (2)4×10-3 Wb/s (3)6 V
(a)
(b)
【变式1】 如图(a)所示,一个圆形线圈的匝数n=1 000,线圈面积S=200 cm2,线圈的电阻r=1 Ω,线圈外接一个阻值R=4 Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化的规律如图(b)所示,求:
(1)前4 s内的感应电动势;
(2)前5 s内的感应电动势。
【答案】(1)1 V (2)0
思考:如图所示,闭合电路一部分导体ab处于匀强磁场中,磁感应强度为B,ab的长度为L,ab以速度v匀速垂直切割磁感线,试利用法拉第电磁感应定律求回路中产生的感应电动势。
探究与思考
1.导体垂直切割磁感线:
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
a
b
v
a
b
匀强磁场的磁感应强度为,长为的导体棒以速度匀速切割磁感线。求产生的感应电动势。
即
二、导体切割磁感线时的感应电动势
动生电动势:由于导体运动而产生的电动势。
θ
v
B
2.导体斜切磁感线与夹角:
二、导体切割磁感线时的感应电动势
注意:1.为切割磁感线的有效长度。
(垂直于、的两端口距离)
× × × × × × × × × × × ×
× × × × × × × × × × × ×
G
v
v
v
× × × ×
× × × ×
× × × ×
× × × ×
v
2. 是的特例,只适用于切割。
3. 为瞬时速度时, 为瞬时感应电动势;
为平均速度时, 为平均感应电动势。
二、导体切割磁感线时的感应电动势
公式E=n 与E=BLvsin α的区别与联系
项目 E=n E=BLvsin α
区别 研究 对象 某个回路 回路中做切割磁感线运动的那部分导体
研究 内容 (1)求的是Δt时间内的平均感应电动势,E与某段时间或某个过程对应 (2)当Δt→0时,E为瞬时感应电动势 (1)若v为瞬时速度,求的是瞬时感应电动势
(2)若v为平均速度,求的是平均感应电动势
(3)当B、L、v三者均不变时,平均感应电动势与瞬时感应电动势相等
适用 范围 对任何电路普遍适用 只适用于导体切割磁感线运动的情况
归纳与总结
联系 (1)E=BLvsin α是由E=n在一定条件下推导出来的
(2)整个回路的感应电动势为零时,回路中某段导体的感应电动势不一定为零
计算感应电动势的方法:
感应电动势
瞬时感应电动势
平均感应电动势
为瞬时速度
为平均速度
功率
瞬时功率
平均功率
为瞬时速度
为平均速度
归纳总结
【例2】如图所示,平行导轨间距为d,其左端接一个电阻R,匀强磁场的磁感应强度为B,方向垂直于平行金属导轨所在平面,一根金属棒与导轨成θ角放置,金属棒与导轨的电阻均不计。当金属棒沿垂直于棒的方向以恒定的速度v在导轨上滑行时,通过电阻R的电流大小是( )
D
典型例题
如图所示,导体棒长为L,磁感应强度为B,方向垂直于纸面向里。
1.以O为圆心转动,角速度为。
判断O、A电势高低;
求感应电动势。
× × × ×
× × × ×
× × × ×
× × × ×
O
L
A
三、导体转动切割磁感线
× × ×
× × ×
× × ×
× × ×
× × ×
× × ×
B
A
O
●
B
A
O
●
2.AO=BO=L。
3.AO=L,BO=。
三、导体转动切割磁感线
4.AB=L,BO=。
导体棒延长至O点,
则AO段有
× × ×
× × ×
× × ×
B
A
O
●
●
法一:补偿法。
BO段有
三、导体转动切割磁感线
4.AB=L,BO=。
A点速度
× × ×
× × ×
× × ×
B
A
O
●
●
法二:求棒上的平均速度。
B点速度
平均速度
●
棒中点速度
●
●
三、导体转动切割磁感线
本课总结
1.关于电磁感应,下述说法中正确的是( )
A.穿过线圈的磁通量越大,感应电动势越大
B.穿过线圈的磁通量为零,感应电动势一定为零
C.穿过线圈的磁通量的变化越大,感应电动势越大
D.穿过线圈的磁通量变化越快,感应电动势越大
D
注意:感应电动势E与Φ、△Φ、 △Φ/△t的关系
Φ/10-2Wb
t/s
A
B
D
0
1
2
0.1
2.单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场。若线圈所围面积里磁通量随时间变化的规律如图所示,则( )
A.线圈中0时刻感应电动势最大 B.线圈中D时刻感应电动势为零 C.线圈中D时刻感应电动势最大 D.线圈中0到D时间内平均感应电动势为0.4V
ABD
斜率表示Φ的变化率
3.(公式E=n 的应用)穿过一个单匝闭合线圈的磁通量始终为每秒均匀增加2 Wb,则( )
A.线圈中感应电动势每秒增加2 V
B.线圈中感应电动势每秒减少2 V
C.线圈中感应电动势始终为2 V
D.线圈中感应电动势始终为一个确定值,但由于线圈有电阻,电动势小于2 V
C
4.(公式E=BLv的应用)如图所示,一金属弯杆处在磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,已知ab=bc=L,当它以速度v向右平动时,a、c两点间的电势差大小为( )
A.BLv
B.BLvsin θ
C.BLvcos θ
D.BLv(1+sin θ)
B
解析:杆切割磁感线的有效长度为Lsin θ,故B正确。
5.如图所示,半径为r的金属圆盘在垂直于盘面的匀强磁场B中,绕O轴以角速度ω沿逆时针方向匀速转动,则通过电阻R的电流的方向和大小是(金属圆盘的电阻不计)( )
A.由c到d,;
B.由d到c,;
C.由c到d,;
D.由d到c,。
D
6.如图所示,线框用裸导线组成,cd、ef两边所在平面与磁感线相互垂直且cd、ef 相互平行,导体棒ab水平放置并可沿cd、ef无摩擦滑动,而导体棒ab所在处的匀强磁场B2=2 T,已知ab长l=0.1 m,整个电路总电阻R=5 Ω。螺线管匝数n=4,螺线管横截面积S=0.1 m2。在螺线管内有图示方向的磁场B1,若=10 T/s恒定不变时,导体棒恰好处于静止状态,求:(g取10 m/s2)
(1)通过导体棒ab的电流大小;
(2)导体棒ab的质量m。
答案:(1)0.8 A (2)0.016 kg
(1)通过导体棒ab的电流大小;
(2)导体棒ab的质量m。
