重庆市凤鸣山中学2023-2024学年八年级下学期3月月考数学试卷(含解析)
文档属性
| 名称 | 重庆市凤鸣山中学2023-2024学年八年级下学期3月月考数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-20 10:57:33 | ||
图片预览




文档简介
重庆市凤鸣山中学2023-2024学年八年级下学期3月月考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.点P(2,-3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知点与点B关于x轴对称,则点B的坐标为( )
A. B. C. D.
3.平面坐标系中点到y轴的距离为( )
A.3 B.4 C.5 D.
4.直线与x轴的交点坐标是( )
A. B. C. D.
5.已知一次函数中,函数值随自变量的增大而减小,那么的取值范围是( ).
A. B. C. D.
6.已知反比例函数的图象在二、四象限,则的取值范围是( )
A. B. C. D.
7.如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为( )
A. B. C. D.
8.反比例函数和一次函数在同一平面直角坐标系的大致图象可能是( )
A. B. C. D.
9.若点、、在反比例函数的图像上,则、、的大小关系为( )
A. B. C. D.
10.甲乙两车从A城出发匀速驶向B城,在整个行驶过程中,两车离开A城的距离与甲车行驶的时间之间的函数关系如图,下列结论正确的有( )个
①A、B两城相距300千米;
②甲车比乙车早出发1小时,却晚到1小时;
③相遇时乙车行驶了2.5小时;
④当甲乙两车相距50千米时,t的值为或或或
A.1 B.2 C.3 D.4
二、填空题
11.函数中,自变量x的取值范围是_____.
12.将直线向上平移4个单位长度,得到的新直线的解析式为_____.
13.若点在y轴上,则p点坐标为_____.
14.已知函数是正比例函数,则_____.
15.已知一次函数与的图象如图所示,且方程组的解为,点B坐标为,y轴上的一个动点P,若,则点P的坐标为_____.
16.若关于x的不等式组无解,且关于y的分式方程有正整数解,则满足条件的所有整数a的和为_____.
17.在平面直角坐标系中,反比例函数的图象交直角梯形的边于点D,交边于点C,且D是边的中点,若四边形的面积为10,_____.
18.一个四位正整数的各个数位上的数字互不相等且均不为0,若满足千位数字与个位数字之和等于百位数字与十位数字之和,则称这个四位数M为“凤鸣数”.若一个“凤鸣数”为,则这个数为 ;将“凤鸣数”的千位数字与十位数字对调,百位数字与个位数字对调得到一个新的四位数N.若N能被9整除,且为整数,则满足条件的M的最大值为_____.
三、解答题
19.计算:
(1);
(2)
20.计算:
(1);
(2)
21.已知函数,与成正比例函数,与x成反比例函数,当时,,当时,.
(1)求y与x的函数关系式;
(2)求当时,y的值.
22.如图,已知中,.
(1)请用基本的尺规作图:作的角平分线交于点D,在上取一点E,使得,连接(不写作法,不下结论,保留作图痕迹):
(2)在(1)所作的图形中,探究线段与之间的数量关系.小明遇到这个问题时,给出了如下的解决思路,请根据小明的思路完成下面的填空.
,理由如下:
∵平分,
∴_____,
在与中,
,
∴,
∴_____,
∵,
∴_____,
∴,
∴_____,
∵,
∴.
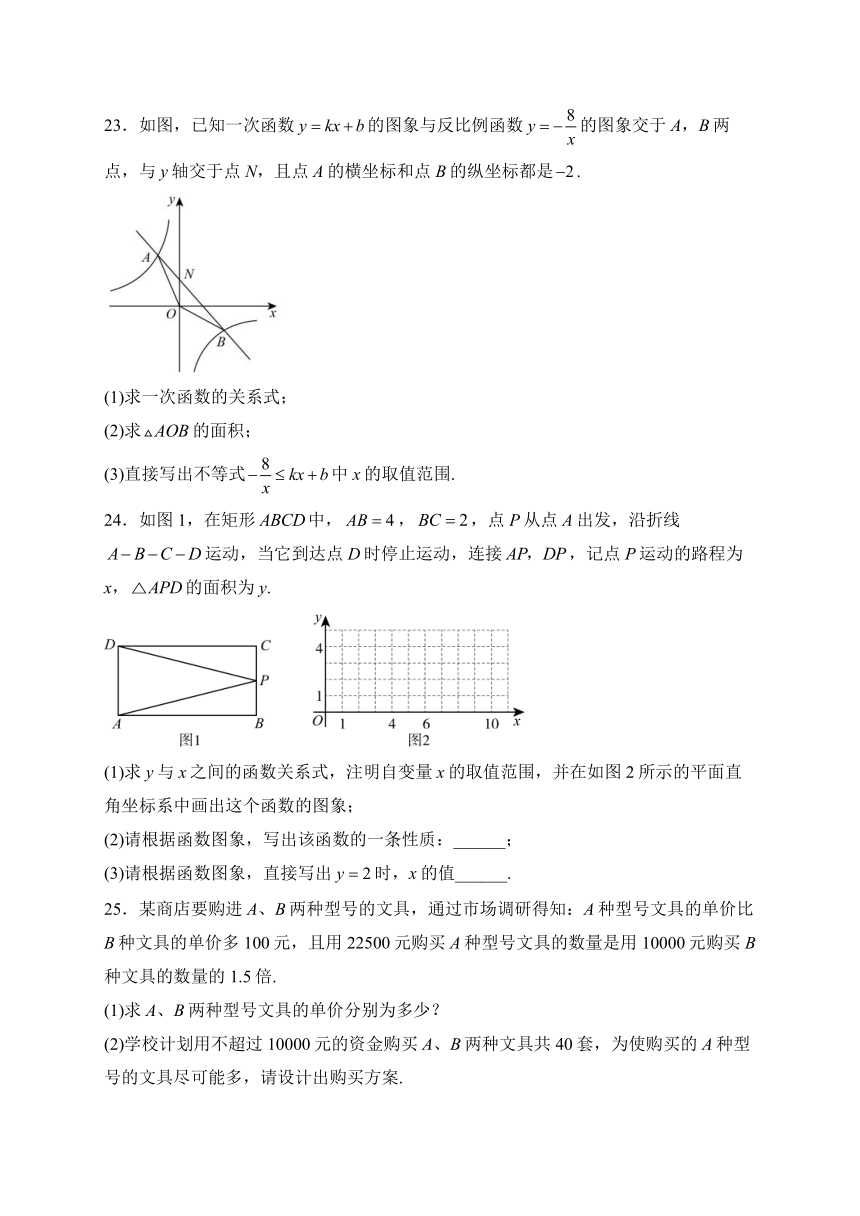
23.如图,已知一次函数的图象与反比例函数的图象交于A,B两点,与y轴交于点N,且点A的横坐标和点B的纵坐标都是.
(1)求一次函数的关系式;
(2)求的面积;
(3)直接写出不等式中x的取值范围.
24.如图1,在矩形中,,,点P从点A出发,沿折线运动,当它到达点D时停止运动,连接,记点P运动的路程为x,的面积为y.
(1)求y与x之间的函数关系式,注明自变量x的取值范围,并在如图2所示的平面直角坐标系中画出这个函数的图象;
(2)请根据函数图象,写出该函数的一条性质:______;
(3)请根据函数图象,直接写出时,x的值______.
25.某商店要购进A、B两种型号的文具,通过市场调研得知:A种型号文具的单价比B种文具的单价多100元,且用22500元购买A种型号文具的数量是用10000元购买B种文具的数量的1.5倍.
(1)求A、B两种型号文具的单价分别为多少?
(2)学校计划用不超过10000元的资金购买A、B两种文具共40套,为使购买的A种型号的文具尽可能多,请设计出购买方案.
26.如图1,在中,,,于点D,点E在边上,连结交于点O,于点F,交于点G.
(1)求证:;
(2)如图2,若点E是边的中点,连结,求证:;
(3)如图3,若点E是边上的动点,连结.当点E在边上(不含端点)运动时,的大小是否改变,如果不变,请直接写出的度数;如果要变,请说明理由.
参考答案
1.答案:D
解析:∵点P的横坐标为正,纵坐标为负,
∴点P(2,-3)所在象限为第四象限.
故选:D.
2.答案:B
解析:∵点关于x轴对称;
∴对称的点的坐标是.
故选:B.
3.答案:B
解析:∵平面直角坐标系中点的坐标为,
∴这点到y轴的距离为4,
故选:B.
4.答案:B
解析:在中,当时,则,
解得:,
则直线与x轴的交点坐标是.
故选:B.
5.答案:C
解析:函数值y随自变量x的增大而减小,那么,
解得.
故选:C.
6.答案:D
解析:因为反比例函数的图象在二、四象限,
所以,解得.
故选:D.
7.答案:A
解析:由图象可以看出,直线y=4上方函数图象所对应自变量的取值为x>-2,
∴不等式kx+b>4的解集是:x>-2,
故选A.
8.答案:B
解析:A.反比例函数图象在第一、三象限,则,一次函数图象应经过二、三、四象限,故此选项错误;
B.反比例函数图象在第一、三象限,则,一次函数图象与y轴正半轴相交,且经过一、二、四象限,故此选项错误;
C.反比例函数图象在第二、四象限,则,一次函数图象应经过一、二、四象限,故此选项错误;
D.反比例函数图象在第一、三象限,则,一次函数图象经过一、二、四象限,故此选项正确.
故选:D.
9.答案:C
解析:点,,在反比例函数的图像上,
,,,
.
故选:C.
10.答案:C
解析:根据题意可知,①两城相距千米,正确;
②甲车比乙车早出发小时,甲走完全程用了小时,乙走完全程用了小时,乙比甲早到小时,正确;
③设甲的路程与时间的函数解析式为,经过,
∴,解得,,
∴甲的路程与时间的函数解析式为,
设乙的路程与时间的函数解析式为,经过,
∴,解得,,
∴乙的路程与时间的函数解析式为,
甲、乙相遇,则,
∴,解得,,
∴相遇时乙车行驶了小时,故③错误;
∵甲的路程与时间的函数解析式为,乙的路程与时间的函数解析式为,
∴情况一:相遇前,甲先走,乙未走,,则,解得,;
乙开始走,,则,解得,;
情况二:相遇后,,则,解得,;
当时,乙到达;当时,;
综上所述,当甲乙两车相距千米时,的值为或或或,故④正确;
∴正确的有:①②④,
故选:C.
11.答案:
解析:由题意,得,
解得:.
故答案为:.
12.答案:
解析:将直线向上平移4个单位长度,得到的新直线的解析式为.
故答案为:.
13.答案:
解析:∵点在y轴上,
∴,
∴,
∴,
∴p点坐标为,
故答案为:.
14.答案:3
解析:∵函数是正比例函数,
∴且,
∴,
∴.
故答案为:3.
15.答案:或
解析:依题意,点A的坐标为,
,
点P在y轴上,点B坐标为,
点P的坐标为或,
故答案为:或.
16.答案:11
解析:解不等式,得.
解不等式,得.
关于的不等式组无解,
.
.
,
.
.
.
.
关于的分式方程有正整数解,
且或或或.
或(当,此时是增根,故舍去)或或.
综上:或7.
满足条件的整数和为.
故答案为:11.
17.答案:
解析:连接,延长交x轴于点E,如图所示:
∵四边形为直角梯形,
∴,
∵,
∴,
∴四边形为矩形,
∴,
∴轴,
∴,
∵D是边的中点,
∴,
∴,
∵,
∴,
∴,
∵反比例函数图象在第二象限,
∴,
∴.
故答案为:.
18.答案:3254;8631
解析:∵是一个“凤鸣数”,
∴,
解得:,
∴这个数为3254;
由题意知,,,
根据“凤鸣数”的定义, 则,
∴.
∵N能被9整除,
∴能被9整除,
∵互不相等且均不为0,
∴.
由以上可知,
∵能被13整除,
∴能被13整除,
∵,
∴能被13整除, 则.
∵取最大值, 则.
即.
故答案为:3254,8631.
19.答案:(1)
(2)
解析:(1)原式
(2)
原式
20.答案:(1)
(2)
解析:(1)
.
(2)
.
21.答案:(1)
(2)
解析:(1)设,
则
把代入得
,
∴
∴
(2)当时
22.答案:(1)图形见解答
(2)∠EAD,DB,∠C,BD
解析:(1)图形如图所示:
(2),理由如下:
∵平分,
∴,
在与中,
,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
故答案为:.
23.答案:(1)
(2)
(3)或
解析:(1)∵点A的横坐标和点B的纵坐标都是,
又∵一次函数的图象与反比例函数的图象交于A,B两点,
∴点A纵坐标为,点B横坐标为,
∴点A坐标为,点B坐标为,
将点,点代入得
,
解得,
∴一次函数解析式为;
(2)∵一次函数与y轴交于点N,
∴点N坐标为,
∴,
∴,
∴的面积为6;
(3)根据图象可知,不等式的解集为或.
24.答案:(1),图象见解析
(2)此图象为轴对称图形,对称轴为直线
(3)2或8
解析:(1)当点P在上时,,
当点P在上时,,
当点P在上时,,
综上所述:,
函数图象如图所示:
(2)由图象可得:此图象为轴对称图形,对称轴为直线;
故答案为:此图象为轴对称图形,对称轴为直线;
(3)当点P在上时,,
当点P在上时,
∴,
综上所述:当时,或8.
故答案为:2或8.
25.答案:(1)购买A种型号文具的单价为300元,购买B种型号文具的单价为200元
(2)购买A种型号玩具20套,购买B种型号玩具20套
解析:(1)设购买B种型号文具的单价为x元,则购买A种型号文具的单价为元
解得,
经检验是原分式方程的解,且符合题意
∴(元)
答:购买A种型号文具的单价为300元,购买B种型号文具的单价为200元;
(2)设购买A种型号玩具m套,则购买B种型号玩具套,根据题意得:
解得,
∴m的最大值为20,此时(套)
答:购买A种型号玩具20套,购买B种型号玩具20套
26.答案:(1)见解析
(2)见解析
(3)不发生变化,,
解析:(1)证明:∵,,于点D,
∴,
∵,
∴,
∴,,
∴,
在与中,,
∴;
(2)证明:如图,过点C作交延长线于点M,
∵,
∴,
在和中,
,
∴,
∴,,,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴;
(3)的大小不会改变,
如图,过点D作,交的延长线于点N,则,
∵,
∴,
∴,即,
∵,,
∴,
在中,,
∴,
在和中,
,
∴,
∴,
又,
∴,
∴.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.点P(2,-3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知点与点B关于x轴对称,则点B的坐标为( )
A. B. C. D.
3.平面坐标系中点到y轴的距离为( )
A.3 B.4 C.5 D.
4.直线与x轴的交点坐标是( )
A. B. C. D.
5.已知一次函数中,函数值随自变量的增大而减小,那么的取值范围是( ).
A. B. C. D.
6.已知反比例函数的图象在二、四象限,则的取值范围是( )
A. B. C. D.
7.如图,直线y=kx+b(k≠0)经过点A(﹣2,4),则不等式kx+b>4的解集为( )
A. B. C. D.
8.反比例函数和一次函数在同一平面直角坐标系的大致图象可能是( )
A. B. C. D.
9.若点、、在反比例函数的图像上,则、、的大小关系为( )
A. B. C. D.
10.甲乙两车从A城出发匀速驶向B城,在整个行驶过程中,两车离开A城的距离与甲车行驶的时间之间的函数关系如图,下列结论正确的有( )个
①A、B两城相距300千米;
②甲车比乙车早出发1小时,却晚到1小时;
③相遇时乙车行驶了2.5小时;
④当甲乙两车相距50千米时,t的值为或或或
A.1 B.2 C.3 D.4
二、填空题
11.函数中,自变量x的取值范围是_____.
12.将直线向上平移4个单位长度,得到的新直线的解析式为_____.
13.若点在y轴上,则p点坐标为_____.
14.已知函数是正比例函数,则_____.
15.已知一次函数与的图象如图所示,且方程组的解为,点B坐标为,y轴上的一个动点P,若,则点P的坐标为_____.
16.若关于x的不等式组无解,且关于y的分式方程有正整数解,则满足条件的所有整数a的和为_____.
17.在平面直角坐标系中,反比例函数的图象交直角梯形的边于点D,交边于点C,且D是边的中点,若四边形的面积为10,_____.
18.一个四位正整数的各个数位上的数字互不相等且均不为0,若满足千位数字与个位数字之和等于百位数字与十位数字之和,则称这个四位数M为“凤鸣数”.若一个“凤鸣数”为,则这个数为 ;将“凤鸣数”的千位数字与十位数字对调,百位数字与个位数字对调得到一个新的四位数N.若N能被9整除,且为整数,则满足条件的M的最大值为_____.
三、解答题
19.计算:
(1);
(2)
20.计算:
(1);
(2)
21.已知函数,与成正比例函数,与x成反比例函数,当时,,当时,.
(1)求y与x的函数关系式;
(2)求当时,y的值.
22.如图,已知中,.
(1)请用基本的尺规作图:作的角平分线交于点D,在上取一点E,使得,连接(不写作法,不下结论,保留作图痕迹):
(2)在(1)所作的图形中,探究线段与之间的数量关系.小明遇到这个问题时,给出了如下的解决思路,请根据小明的思路完成下面的填空.
,理由如下:
∵平分,
∴_____,
在与中,
,
∴,
∴_____,
∵,
∴_____,
∴,
∴_____,
∵,
∴.
23.如图,已知一次函数的图象与反比例函数的图象交于A,B两点,与y轴交于点N,且点A的横坐标和点B的纵坐标都是.
(1)求一次函数的关系式;
(2)求的面积;
(3)直接写出不等式中x的取值范围.
24.如图1,在矩形中,,,点P从点A出发,沿折线运动,当它到达点D时停止运动,连接,记点P运动的路程为x,的面积为y.
(1)求y与x之间的函数关系式,注明自变量x的取值范围,并在如图2所示的平面直角坐标系中画出这个函数的图象;
(2)请根据函数图象,写出该函数的一条性质:______;
(3)请根据函数图象,直接写出时,x的值______.
25.某商店要购进A、B两种型号的文具,通过市场调研得知:A种型号文具的单价比B种文具的单价多100元,且用22500元购买A种型号文具的数量是用10000元购买B种文具的数量的1.5倍.
(1)求A、B两种型号文具的单价分别为多少?
(2)学校计划用不超过10000元的资金购买A、B两种文具共40套,为使购买的A种型号的文具尽可能多,请设计出购买方案.
26.如图1,在中,,,于点D,点E在边上,连结交于点O,于点F,交于点G.
(1)求证:;
(2)如图2,若点E是边的中点,连结,求证:;
(3)如图3,若点E是边上的动点,连结.当点E在边上(不含端点)运动时,的大小是否改变,如果不变,请直接写出的度数;如果要变,请说明理由.
参考答案
1.答案:D
解析:∵点P的横坐标为正,纵坐标为负,
∴点P(2,-3)所在象限为第四象限.
故选:D.
2.答案:B
解析:∵点关于x轴对称;
∴对称的点的坐标是.
故选:B.
3.答案:B
解析:∵平面直角坐标系中点的坐标为,
∴这点到y轴的距离为4,
故选:B.
4.答案:B
解析:在中,当时,则,
解得:,
则直线与x轴的交点坐标是.
故选:B.
5.答案:C
解析:函数值y随自变量x的增大而减小,那么,
解得.
故选:C.
6.答案:D
解析:因为反比例函数的图象在二、四象限,
所以,解得.
故选:D.
7.答案:A
解析:由图象可以看出,直线y=4上方函数图象所对应自变量的取值为x>-2,
∴不等式kx+b>4的解集是:x>-2,
故选A.
8.答案:B
解析:A.反比例函数图象在第一、三象限,则,一次函数图象应经过二、三、四象限,故此选项错误;
B.反比例函数图象在第一、三象限,则,一次函数图象与y轴正半轴相交,且经过一、二、四象限,故此选项错误;
C.反比例函数图象在第二、四象限,则,一次函数图象应经过一、二、四象限,故此选项错误;
D.反比例函数图象在第一、三象限,则,一次函数图象经过一、二、四象限,故此选项正确.
故选:D.
9.答案:C
解析:点,,在反比例函数的图像上,
,,,
.
故选:C.
10.答案:C
解析:根据题意可知,①两城相距千米,正确;
②甲车比乙车早出发小时,甲走完全程用了小时,乙走完全程用了小时,乙比甲早到小时,正确;
③设甲的路程与时间的函数解析式为,经过,
∴,解得,,
∴甲的路程与时间的函数解析式为,
设乙的路程与时间的函数解析式为,经过,
∴,解得,,
∴乙的路程与时间的函数解析式为,
甲、乙相遇,则,
∴,解得,,
∴相遇时乙车行驶了小时,故③错误;
∵甲的路程与时间的函数解析式为,乙的路程与时间的函数解析式为,
∴情况一:相遇前,甲先走,乙未走,,则,解得,;
乙开始走,,则,解得,;
情况二:相遇后,,则,解得,;
当时,乙到达;当时,;
综上所述,当甲乙两车相距千米时,的值为或或或,故④正确;
∴正确的有:①②④,
故选:C.
11.答案:
解析:由题意,得,
解得:.
故答案为:.
12.答案:
解析:将直线向上平移4个单位长度,得到的新直线的解析式为.
故答案为:.
13.答案:
解析:∵点在y轴上,
∴,
∴,
∴,
∴p点坐标为,
故答案为:.
14.答案:3
解析:∵函数是正比例函数,
∴且,
∴,
∴.
故答案为:3.
15.答案:或
解析:依题意,点A的坐标为,
,
点P在y轴上,点B坐标为,
点P的坐标为或,
故答案为:或.
16.答案:11
解析:解不等式,得.
解不等式,得.
关于的不等式组无解,
.
.
,
.
.
.
.
关于的分式方程有正整数解,
且或或或.
或(当,此时是增根,故舍去)或或.
综上:或7.
满足条件的整数和为.
故答案为:11.
17.答案:
解析:连接,延长交x轴于点E,如图所示:
∵四边形为直角梯形,
∴,
∵,
∴,
∴四边形为矩形,
∴,
∴轴,
∴,
∵D是边的中点,
∴,
∴,
∵,
∴,
∴,
∵反比例函数图象在第二象限,
∴,
∴.
故答案为:.
18.答案:3254;8631
解析:∵是一个“凤鸣数”,
∴,
解得:,
∴这个数为3254;
由题意知,,,
根据“凤鸣数”的定义, 则,
∴.
∵N能被9整除,
∴能被9整除,
∵互不相等且均不为0,
∴.
由以上可知,
∵能被13整除,
∴能被13整除,
∵,
∴能被13整除, 则.
∵取最大值, 则.
即.
故答案为:3254,8631.
19.答案:(1)
(2)
解析:(1)原式
(2)
原式
20.答案:(1)
(2)
解析:(1)
.
(2)
.
21.答案:(1)
(2)
解析:(1)设,
则
把代入得
,
∴
∴
(2)当时
22.答案:(1)图形见解答
(2)∠EAD,DB,∠C,BD
解析:(1)图形如图所示:
(2),理由如下:
∵平分,
∴,
在与中,
,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
故答案为:.
23.答案:(1)
(2)
(3)或
解析:(1)∵点A的横坐标和点B的纵坐标都是,
又∵一次函数的图象与反比例函数的图象交于A,B两点,
∴点A纵坐标为,点B横坐标为,
∴点A坐标为,点B坐标为,
将点,点代入得
,
解得,
∴一次函数解析式为;
(2)∵一次函数与y轴交于点N,
∴点N坐标为,
∴,
∴,
∴的面积为6;
(3)根据图象可知,不等式的解集为或.
24.答案:(1),图象见解析
(2)此图象为轴对称图形,对称轴为直线
(3)2或8
解析:(1)当点P在上时,,
当点P在上时,,
当点P在上时,,
综上所述:,
函数图象如图所示:
(2)由图象可得:此图象为轴对称图形,对称轴为直线;
故答案为:此图象为轴对称图形,对称轴为直线;
(3)当点P在上时,,
当点P在上时,
∴,
综上所述:当时,或8.
故答案为:2或8.
25.答案:(1)购买A种型号文具的单价为300元,购买B种型号文具的单价为200元
(2)购买A种型号玩具20套,购买B种型号玩具20套
解析:(1)设购买B种型号文具的单价为x元,则购买A种型号文具的单价为元
解得,
经检验是原分式方程的解,且符合题意
∴(元)
答:购买A种型号文具的单价为300元,购买B种型号文具的单价为200元;
(2)设购买A种型号玩具m套,则购买B种型号玩具套,根据题意得:
解得,
∴m的最大值为20,此时(套)
答:购买A种型号玩具20套,购买B种型号玩具20套
26.答案:(1)见解析
(2)见解析
(3)不发生变化,,
解析:(1)证明:∵,,于点D,
∴,
∵,
∴,
∴,,
∴,
在与中,,
∴;
(2)证明:如图,过点C作交延长线于点M,
∵,
∴,
在和中,
,
∴,
∴,,,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴;
(3)的大小不会改变,
如图,过点D作,交的延长线于点N,则,
∵,
∴,
∴,即,
∵,,
∴,
在中,,
∴,
在和中,
,
∴,
∴,
又,
∴,
∴.
同课章节目录
