人教版四年级数学下册 小数比大小课件(共19张PPT)
文档属性
| 名称 | 人教版四年级数学下册 小数比大小课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 461.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-20 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
——《小数比大小》一课的教学思考
在比较中学习
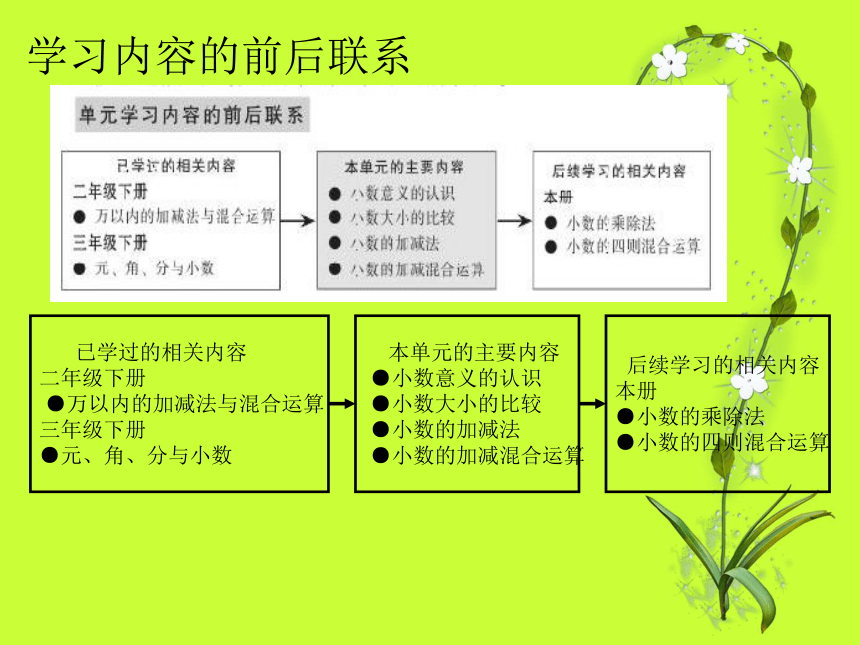
学习内容的前后联系
已学过的相关内容
二年级下册
●万以内的加减法与混合运算
三年级下册
●元、角、分与小数
本单元的主要内容
●小数意义的认识
●小数大小的比较
●小数的加减法
●小数的加减混合运算
后续学习的相关内容
本册
●小数的乘除法
●小数的四则混合运算
《小数比大小》学生已有的经验:
生活经验:
对两个商品价钱的高低比较经验
学习经验:
整数比大小的经验
三年级学习了“小数的初步认识”会借助“元、角、分”和“米、分米、厘米”比较两个数的大小
抽查发现:
学生基本上会进行小数大小的比较,
问他们怎么比的?基本上的回答是:从
高位比起,一位一位比较。
容易出错的地方比如比较7.19○7.2时,
有的学生会出现7.19﹥7.2的错误。原因
是:数位多的这个小数就大。
思考:
本课的教学定位到底是什么
学生已经有了小数比大小的感觉,但还
是没有形成科学的比较方法。
有的学生会比较小数大小,但是对于
为什么这样比,却说不清道理。
本课的目标:
1、会比较两个及多个小数的大小。
2、在比较小数大小的过程中,发现比较的原理。
3、学会在比较中学习的思想方法。
教学设计:
第一层次:首先复习整数大小的比较,巩固整数大小的比较方法。
第二层次:比较两个小数的大小,让学生通过自己的比较、观察,
发现小数大小的比较方法
第三层次:找出这些大小比较方法之间的相同点和不同点。及与
整数大小比较的相同点和不同点。
第四层次:把多个小数按要求进行排列,掌握并巩固小数的比较方法。
第五层次:巩固练习
突破为什么这样比的道理
二、创设情境,引发思考
1、利用跳远纪录单引出小数的大小比较
(课件出现:A.3.84米 B.4.01米 C.3.□9米)
师:这里有一张跳远成绩记录单,很遗憾,有点缺陷,但现在通过记录单你能知道什么?
生:我知道B跳得最远。
师:你从哪看出来的?
生:因为只有B跳了4米多,而A和C都是3米多。
师:很好,我们从整数部分找到了第一名。老师适时板书出:整数部分不同,
整数部分谁大那个数就大。那第二名又是谁呢?
生:不一定。
师:听你们的意思,决定第二名需要分情况,对吗?
生:对
师:那好,假设C是第二名会怎样?
生:那C可能是3.89米。
生:也可能是3.99米
师:看来不止一种情况,但有可能是3.89米,你们认为3.89要比3.84
生:大
师:那你们有充分地理由说明3.89比3.84大吗?
(生互相交流后回答)
生1:3.89和3.84的整数部分都是3,十分位都是8,而百分位9比4大,
所以3.89大于3.84。
师:哦,一位一位地比较出大小关系,老师适时板书出:整数部分相同:
从十分位顺次比较。谁和他想的一样?
(大部分学生举手)
生2:3.89表示有389个0.01,而3.84表示384个0.01。389大于384,所以3.89大于3.84。
生3:3.89表示389/1000, 3.84表示384/1000。因为389/1000大于384/1000,
所以3.89大于3.84。
生4:3.89米就是389厘米,3.84米就是384厘米。389厘米大于384厘米,
所以3.89米大于3.84米。
2、沟通小数大小比较方法之间的联系与区别
师:比较刚才这四位同学的方法你有什么发现
生:他们都进行了转化,转化成整数比大小。(师适时板书:转化)
师:这些方法的区别是什么?
生:只是转化后的单位不一样,一个是小数的计数单位,一个是分数的计数单位,
一个是以1厘米为单位。第一位同学一位一位比也是相同的单位在比大小。
师:真厉害!火眼金晶,能在这么多方法中找到相同点。
(适时板书:单位相同再比大小)
师:这些方法是不是适合所有小数大小的比较呢?
三、列举小数,梳理比较方法
1、列举小数
师:我们来列举几个小数,如:7.2
请你列举一个整数部分是0的两位小数?
生:0.32
举一个整数部分是0的三位小数?
生:0.542
比它大0.001的小数?
生:0.543
师写两个:7.19 0.320
2、选择小数进行比较
师:7个小数中请你任选两个小数比大小,你准备怎么比?
生列举师板书:
7.2○0.32 7.2○0.543 7.19○0.542
7.19○7.2 0.32○0.542 0.542○0.543 0.32○0.320
3、比一比
请一个小组开火车比一比,填一填。
7.2﹥0.32 7.2﹥0.543 7.19﹥0.542
7.19﹤7.2 0.32﹤0.542 0.542﹤0.543 0.32﹦0.320
4、说一说比较的方法
说一说:7.2﹥0.32,你是怎么比的?
生:先比整数部分,整数部分谁大那个数就大。
师:用这种方法比出来的还有吗?
生:7.2﹥0.543 7.19﹥0.542也是这样比的
师:这三题如果用转化的思想能比吗?
生:7.2就是72个0.1,0.32就是32个0.01。数位不同,计数单位也不同无法比较。
生:我可以把7.2变成7.20,这样就可以用720个0.01和32个0.01比较了。
师:听明白他的意思了吗?
生:单位相同就可以化成整数比较了,但是这样比较不方便。
说一说7.19﹤7.2怎么比的?
生:整数部分相同,先比十分位,十分位相同,再比百分位,……依次比较。
师:能化成整数比吗?
生:不方便,直接转化719个0.01与72个0.1单位不相同。把7.2变成7.20单位相同
可以比较。
说一说0.542﹤0.543怎么比的?
生:整数部分相同,相比十分位,十分位相同;再比百分位,百分位相同;
比千分位,依次类推。直到比出大小为止。
说一说0.32﹦0.320
生:大小相等
师:有没有不同的地方
生:意义不同,32个0.01 320个0.001
5、小结
师:梳理一下刚才做了一件什么事?
生:小数比较的方法
师:通过刚才的比较,你有什么收获吗?
生:小数比大小分整数部分不同与整数相同两类来比。小数比大小
与整数比大小有点像,都是一位一位比。
师:小数比大小与整数比大小最大的区别是什么?
生:整数先看数位的多少,而小数不能直接看数位的多少。
师:为什么小数不能直接看数位的多少?
生:因为小数越往右计数单位越小,它的数位不一样,计数单位就不一样。
所以,不能直接看数位的多少来比大小。而整数的最后一位肯定是个位,
它的计数单位是确定的,所以,可以直接看数位的多少来比大小。
小数比大小
3.89米 ﹥ 3.84米
7.2 7.2﹥0.32 整数部分不同:
389个0.01﹥384个0.01 0.32 7.2﹥0.543 整数部分谁大那个数就大
389/100﹥384/100 0.542 7.19﹥0.542
389厘米﹥384厘米 0.543 7.19﹤7.2 整数部分相同:
7.19 0.32﹤0.542 从十分位顺次比较
0.320 0.542﹤0.543
转化: 0.32﹦0.320
单位相同再比大小
板书设计:
理
法
后续:
小数加减计算
小数的乘法
0.2
×0.3
0.06
0.2
×0.3
0.6
0.13
×0.2
0.26
2.1 5
× 2.1
2 1 5
4 3 0
4.5 1 5
2 1 5
× 2 1
2 1 5
4 3 0
4 5 1 5
转化
15个0.1
谢谢聆听
——《小数比大小》一课的教学思考
在比较中学习
学习内容的前后联系
已学过的相关内容
二年级下册
●万以内的加减法与混合运算
三年级下册
●元、角、分与小数
本单元的主要内容
●小数意义的认识
●小数大小的比较
●小数的加减法
●小数的加减混合运算
后续学习的相关内容
本册
●小数的乘除法
●小数的四则混合运算
《小数比大小》学生已有的经验:
生活经验:
对两个商品价钱的高低比较经验
学习经验:
整数比大小的经验
三年级学习了“小数的初步认识”会借助“元、角、分”和“米、分米、厘米”比较两个数的大小
抽查发现:
学生基本上会进行小数大小的比较,
问他们怎么比的?基本上的回答是:从
高位比起,一位一位比较。
容易出错的地方比如比较7.19○7.2时,
有的学生会出现7.19﹥7.2的错误。原因
是:数位多的这个小数就大。
思考:
本课的教学定位到底是什么
学生已经有了小数比大小的感觉,但还
是没有形成科学的比较方法。
有的学生会比较小数大小,但是对于
为什么这样比,却说不清道理。
本课的目标:
1、会比较两个及多个小数的大小。
2、在比较小数大小的过程中,发现比较的原理。
3、学会在比较中学习的思想方法。
教学设计:
第一层次:首先复习整数大小的比较,巩固整数大小的比较方法。
第二层次:比较两个小数的大小,让学生通过自己的比较、观察,
发现小数大小的比较方法
第三层次:找出这些大小比较方法之间的相同点和不同点。及与
整数大小比较的相同点和不同点。
第四层次:把多个小数按要求进行排列,掌握并巩固小数的比较方法。
第五层次:巩固练习
突破为什么这样比的道理
二、创设情境,引发思考
1、利用跳远纪录单引出小数的大小比较
(课件出现:A.3.84米 B.4.01米 C.3.□9米)
师:这里有一张跳远成绩记录单,很遗憾,有点缺陷,但现在通过记录单你能知道什么?
生:我知道B跳得最远。
师:你从哪看出来的?
生:因为只有B跳了4米多,而A和C都是3米多。
师:很好,我们从整数部分找到了第一名。老师适时板书出:整数部分不同,
整数部分谁大那个数就大。那第二名又是谁呢?
生:不一定。
师:听你们的意思,决定第二名需要分情况,对吗?
生:对
师:那好,假设C是第二名会怎样?
生:那C可能是3.89米。
生:也可能是3.99米
师:看来不止一种情况,但有可能是3.89米,你们认为3.89要比3.84
生:大
师:那你们有充分地理由说明3.89比3.84大吗?
(生互相交流后回答)
生1:3.89和3.84的整数部分都是3,十分位都是8,而百分位9比4大,
所以3.89大于3.84。
师:哦,一位一位地比较出大小关系,老师适时板书出:整数部分相同:
从十分位顺次比较。谁和他想的一样?
(大部分学生举手)
生2:3.89表示有389个0.01,而3.84表示384个0.01。389大于384,所以3.89大于3.84。
生3:3.89表示389/1000, 3.84表示384/1000。因为389/1000大于384/1000,
所以3.89大于3.84。
生4:3.89米就是389厘米,3.84米就是384厘米。389厘米大于384厘米,
所以3.89米大于3.84米。
2、沟通小数大小比较方法之间的联系与区别
师:比较刚才这四位同学的方法你有什么发现
生:他们都进行了转化,转化成整数比大小。(师适时板书:转化)
师:这些方法的区别是什么?
生:只是转化后的单位不一样,一个是小数的计数单位,一个是分数的计数单位,
一个是以1厘米为单位。第一位同学一位一位比也是相同的单位在比大小。
师:真厉害!火眼金晶,能在这么多方法中找到相同点。
(适时板书:单位相同再比大小)
师:这些方法是不是适合所有小数大小的比较呢?
三、列举小数,梳理比较方法
1、列举小数
师:我们来列举几个小数,如:7.2
请你列举一个整数部分是0的两位小数?
生:0.32
举一个整数部分是0的三位小数?
生:0.542
比它大0.001的小数?
生:0.543
师写两个:7.19 0.320
2、选择小数进行比较
师:7个小数中请你任选两个小数比大小,你准备怎么比?
生列举师板书:
7.2○0.32 7.2○0.543 7.19○0.542
7.19○7.2 0.32○0.542 0.542○0.543 0.32○0.320
3、比一比
请一个小组开火车比一比,填一填。
7.2﹥0.32 7.2﹥0.543 7.19﹥0.542
7.19﹤7.2 0.32﹤0.542 0.542﹤0.543 0.32﹦0.320
4、说一说比较的方法
说一说:7.2﹥0.32,你是怎么比的?
生:先比整数部分,整数部分谁大那个数就大。
师:用这种方法比出来的还有吗?
生:7.2﹥0.543 7.19﹥0.542也是这样比的
师:这三题如果用转化的思想能比吗?
生:7.2就是72个0.1,0.32就是32个0.01。数位不同,计数单位也不同无法比较。
生:我可以把7.2变成7.20,这样就可以用720个0.01和32个0.01比较了。
师:听明白他的意思了吗?
生:单位相同就可以化成整数比较了,但是这样比较不方便。
说一说7.19﹤7.2怎么比的?
生:整数部分相同,先比十分位,十分位相同,再比百分位,……依次比较。
师:能化成整数比吗?
生:不方便,直接转化719个0.01与72个0.1单位不相同。把7.2变成7.20单位相同
可以比较。
说一说0.542﹤0.543怎么比的?
生:整数部分相同,相比十分位,十分位相同;再比百分位,百分位相同;
比千分位,依次类推。直到比出大小为止。
说一说0.32﹦0.320
生:大小相等
师:有没有不同的地方
生:意义不同,32个0.01 320个0.001
5、小结
师:梳理一下刚才做了一件什么事?
生:小数比较的方法
师:通过刚才的比较,你有什么收获吗?
生:小数比大小分整数部分不同与整数相同两类来比。小数比大小
与整数比大小有点像,都是一位一位比。
师:小数比大小与整数比大小最大的区别是什么?
生:整数先看数位的多少,而小数不能直接看数位的多少。
师:为什么小数不能直接看数位的多少?
生:因为小数越往右计数单位越小,它的数位不一样,计数单位就不一样。
所以,不能直接看数位的多少来比大小。而整数的最后一位肯定是个位,
它的计数单位是确定的,所以,可以直接看数位的多少来比大小。
小数比大小
3.89米 ﹥ 3.84米
7.2 7.2﹥0.32 整数部分不同:
389个0.01﹥384个0.01 0.32 7.2﹥0.543 整数部分谁大那个数就大
389/100﹥384/100 0.542 7.19﹥0.542
389厘米﹥384厘米 0.543 7.19﹤7.2 整数部分相同:
7.19 0.32﹤0.542 从十分位顺次比较
0.320 0.542﹤0.543
转化: 0.32﹦0.320
单位相同再比大小
板书设计:
理
法
后续:
小数加减计算
小数的乘法
0.2
×0.3
0.06
0.2
×0.3
0.6
0.13
×0.2
0.26
2.1 5
× 2.1
2 1 5
4 3 0
4.5 1 5
2 1 5
× 2 1
2 1 5
4 3 0
4 5 1 5
转化
15个0.1
谢谢聆听
