2023-2024学年苏教版五年级下册数学第一单元《简易方程》检测卷(含解析)
文档属性
| 名称 | 2023-2024学年苏教版五年级下册数学第一单元《简易方程》检测卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 277.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-20 00:00:00 | ||
图片预览




文档简介
2023-2024学年五年级下册数学单元检测卷
第一单元《简易方程》
姓名:_________ 班级:_________ 学号:_________
一、填空题(共20分)
1.有两桶油,第一桶油是第二桶油的1.5倍,如果从第一桶中倒入第二桶2千克,两桶油相等,第一桶油原来有()千克。
2.父亲比儿子大30岁,明年父亲的年龄是儿子的3倍,那么今年儿子()岁。
3.4年前,妈妈的年龄正好是小雨年龄的4倍,今年妈妈比小雨大27岁。今年妈妈()岁,小雨()岁。
4.如下图,一张收据被墨汁污损了,每张桌子的价格是()元。
5.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲每分钟跑270米,乙每分钟跑230米,经过()分甲第一次追上乙。
6.观察下面两组等式,你有什么发现?
17+8=25 17+8-5=25-5 17+8+10=25+10 20×3=60 20×3×4=60×4 20×3÷2=60÷2
发现一:____________________________;
发现二:____________________________。
7.小明和小红带同样多的钱去买练习本,小明买了6本后把剩下的4元借给小红,这样正好够小红买10本同样的练习本,他们各带了()元钱。
8.鞋的尺码通常用“码”和“厘米”作单位,它们之间的换算关系是y=2x-10(y表示鞋的码数,x表厘米数)。乐乐的爸爸穿43码的鞋,他的脚长是()厘米。乐乐的妈妈的脚长是23厘米,她需要穿()码的鞋。
9.看图列方程。
10.在①x+7.9<16,②0.23m=4.6,③55>m÷0.4,④15×2.4=36,⑤66-x=38中,等式有(),方程有()。(填序号)
二、判断题(共10分)
11.甲、乙共有50本书,甲给乙8本,则两人的本数相同,求甲、乙原有书的本数。用方程解,设乙原来有x本书,列方程式x+x+8=50。()
12.一个直角梯形上底是下底的一半,面积是12平方厘米(上下底和直角边的腰长都是整厘米)。这样不同的直角梯形共有3种。()
13.36-x=14,方程的两边可以同时加x,方程的解不变。()
14.如果x÷1.5=4,那么x÷1.5=4×1.5。()
15.3x+18=30和28-2x=20这两个方程的解相同。()
三、选择题(共10分)
16.已知2a=3b(a为非零自然数),根据等式的性质,下面等式( )不成立。
A.20a=30b B.2a-5=3b-5 C.2a+2=3b+3 D.2a÷2=3b÷2
17.如图,有甲、乙、丙三根绳子,丙绳子的长度是( )分米。
A.50-35-x B.50-x+35 C.50-35+x D.35-(50-x)
18.甲有a枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等。下面等式正确的是( )。
A.a-8=15 B.a=15-8 C.a-8=15+8 D.a=15+16
19.在13b+5>23,x+2.4x=30,45×3=135,1.5m=70,8n-3.6中,方程有( )个。
A.3 B.4 C.2 D.1
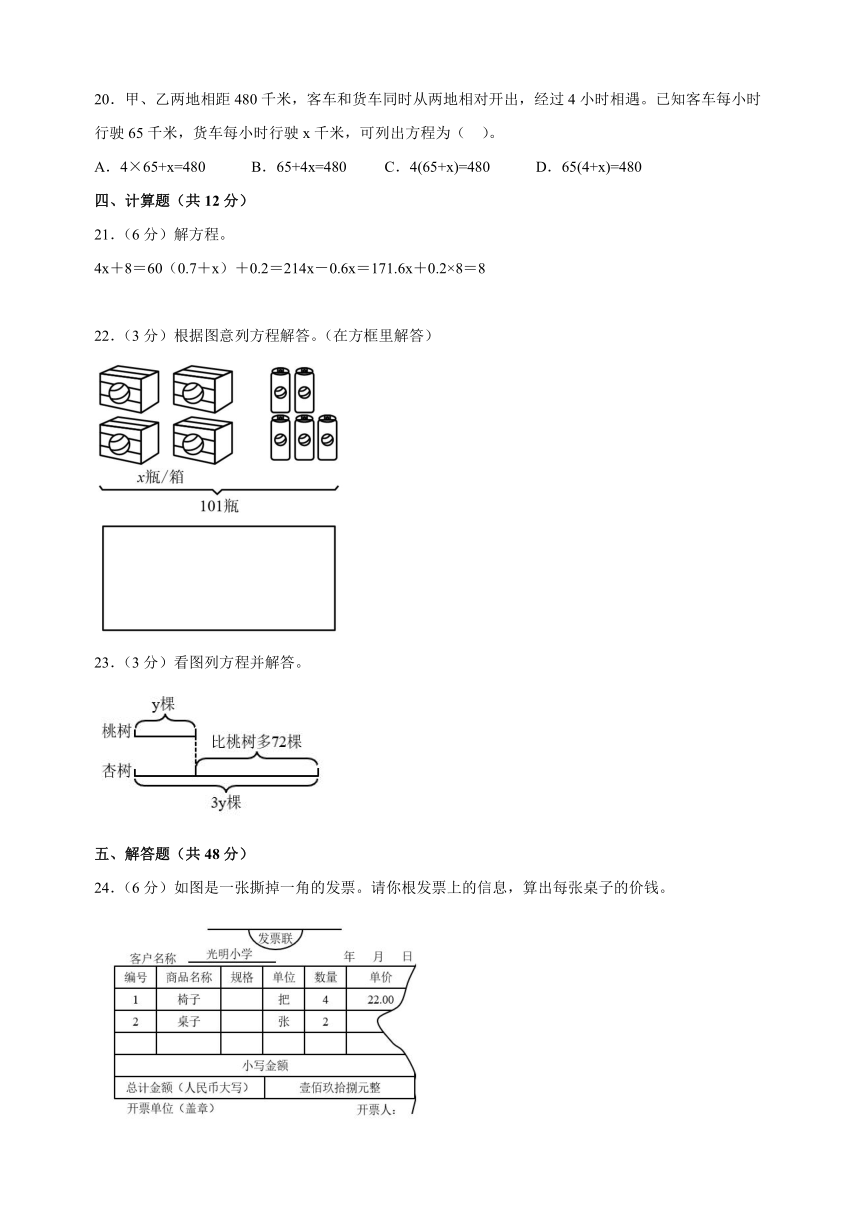
20.甲、乙两地相距480千米,客车和货车同时从两地相对开出,经过4小时相遇。已知客车每小时行驶65千米,货车每小时行驶x千米,可列出方程为( )。
A.4×65+x=480 B.65+4x=480 C.4(65+x)=480 D.65(4+x)=480
四、计算题(共12分)
21.(6分)解方程。
4x+8=60(0.7+x)+0.2=214x-0.6x=171.6x+0.2×8=8
22.(3分)根据图意列方程解答。(在方框里解答)
23.(3分)看图列方程并解答。
五、解答题(共48分)
24.(6分)如图是一张撕掉一角的发票。请你根发票上的信息,算出每张桌子的价钱。
25.(6分)为了开发城市旅游业,某城市打算建设一处花海基地约150公顷,共种植三种颜色的花,红色花区面积约80公顷,蓝色花区的面积比黄色花区的3倍少10公顷,蓝色、黄色花区的面积各约为多少公顷?(列方程解答)
26.(6分)2021年5月29日,我国成功发射天舟二号货运飞船,飞船此行的主要任务是把航天员和空间站所需的物资送上天,物资包括货包和推进剂两大类,其中货包的质量约是推进剂的2.4倍,货包的质量比推进剂多2.8吨,货包和推进剂的质量各是多少吨?(先列方程解答,再检验。)
27.(6分)
小红和小军各收集了多少枚邮票?(列方程解答,再用“把得数代入原题”的方法检验)
28.(6分)颐和园是我国保存最完整的一座皇家行宫御苑,被誉为“皇家园林博物馆”,占地面积约为2.9平方千米,比世界上面积最小的国家——梵蒂冈的面积的7倍少0.18平方千米。梵蒂冈的面积约是多少平方千米?(列方程解答)
29.(6分)我们的地球是一个美丽的蓝色星球。朵朵同学借助网络查阅了相关资料,了解到地球的表面积一共约5.1亿平方千米。其中海洋面积大约是陆地面积的2.4倍。请你算一算地球上的海洋面积是多少亿平方千米?
30.(6分)同学们参观“第十二届江苏省园艺博览会博览园”。五、六年级共去286人,六年级去的人数是五年级的1.2倍。两个年级各去多少人?(先把数量关系式填写完整,再用方程解答)
( )+( )=五、六年级一共的人数
31.(6分)在2021年度“众志成城,抗击疫情”爱心捐赠活动中,大众药店和吉祥药店一共捐赠了8000个口罩。大众药店捐赠的口罩数是吉祥药店的1.5倍,两个药店各捐赠了多少个口罩?(用方程解)
参考答案
1.12
【分析】设第二桶油原来有x千克,第一桶油是第二桶油的1.5倍,则第一桶油原来有1.5x千克,如果从第一桶中倒入第二桶2千克,两桶油相等,即第一桶油原来的质量-2千克=第二桶油原来的质量+2千克,列方程:1.5x-2=x+2,解方程,即可解答。
【详解】解:设第二桶油原来有x千克,则第一桶油原来有1.5x千克。
1.5x-2=x+2
1.5x-x=2+2
0.5x=4
x=4÷0.5
x=8
1.5×8=12(千克)
有两桶油,第一桶油是第二桶油的1.5倍,如果从第一桶中倒入第二桶2千克,两桶油相等,第一桶油原来有12千克。
【点睛】本题考查方程的实际应用,根据第一桶油原来的质量与第二桶油原来的质量关系,设出未知数,找出相关的量,列方程,解方程。
2.14
【分析】不论经过多少年,父亲和儿子的年龄差不变;设儿子明年x岁,明年父亲的年龄是儿子的3倍,则父亲明年的年龄是3x岁,父亲比儿子大30岁,列方程:3x-x=30,解方程,求出儿子明年的年龄,再减去1,即可求出今年的年龄。
【详解】解:设明年儿子的年龄x岁,明年父亲的年龄3x岁。
3x-x=30
2x=30
2x÷2=30÷2
x=15
15-1=14(岁)
父亲比儿子大30岁,明年父亲的年龄是儿子的3倍,那么今年儿子14岁。
【点睛】本题考查方程的实际应用。根据父亲与儿子的年龄差不变,设出未知数,找出相关的量,列方程,解方程。
3.40 13
【分析】不管过去多少年,妈妈和小雨的年龄差是不会变的;4年前小雨和妈妈相差27岁。设小雨4年前是x岁,妈妈的年龄正好是小雨年龄的4倍,则妈妈的年龄是4x岁,妈妈的年龄-小雨的年龄=27,解方程:4x-x=27,求出小雨4年前的年龄和妈妈4年前的妈妈的年龄,再用小雨4年前的年龄+4,求出小雨今年的年龄;妈妈的年龄+4,求出妈妈今年的年龄,据此解答。
【详解】解:设4年前小雨x岁,则妈妈4x岁。
4x-x=27
3x=27
3x÷3=27÷3
x=9
妈妈4年前的年龄是:9×4=36(岁)
小雨今年年龄:9+4=13(岁)
妈妈今年年龄:36+4=40(岁)
4年前,妈妈的年龄正好是小雨年龄的4倍,今年妈妈比小雨大27岁。今年妈妈40岁,小雨13岁。
【点睛】本题考查方程的实际应用,利用小雨与妈妈年龄之间的关系,设出未知数,找出相关的量,列方程,解方程;关键明确年龄差是不变的。
4.67
【分析】根据单价×数量=总价,可得椅子的单价×椅子的数量+桌子的单价×桌子的数量=284元,设每张桌子的价格是x元,据此列方程为:2x+6×25=284,然后解出方程即可。
【详解】解:设每张桌子的价格是x元。
2x+6×25=284
2x+150=284
2x+150-150=284-150
2x=134
2x÷2=134÷2
x=67
每张桌子的价格是67元。
【点睛】本题可用列方程解决问题,找到相应的数量关系式是解答本题的关键。
5.10
【分析】根据题意可知,甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行,相当于两人在直线上相距400米,从同一地点出发,同向而行,根据速度差×追及时间=路程差,设经过x分甲第一次追上乙,列方程为(270-230)x=400,然后解出方程即可。
【详解】解:设经过x分甲第一次追上乙。
(270-230)x=400
40x=400
40x÷40=400÷40
x=10
经过10分甲第一次追上乙。
【点睛】本题可用列方程解决问题,找到相应的数量关系式是解答本题的关键。
6.在加法算式中,两边同时加上或减去同一个数,所得结果仍然是等式在乘法算式中,两边同时乘或除以同一个数(0除外),所得结果仍然是等式
【分析】通过观察可知:在等式的两边同时加或减同一个数,等式仍然成立;在等式两边同时乘或除以同一个不为零的数,等式仍然成立。据此解答。
【详解】发现一:在加法算式中,两边同时加上或减去同一个数,所得结果仍然是等式。
发现二:在乘法算式中,两边同时乘或除以同一个数(0除外),所得结果仍然是等式
【点睛】从等式中找到、发现规律是解答的关键。
7.16
【分析】设每本练习册价钱是x元,小明买了6本,花了6x元;小红买了10本,花了10x元。小明买了6本后把剩下的4元借给小红,小明买6本练习册的钱数+4元=小明带的钱数;小红买10本练习册的钱数-4元=小红带的钱数,小明和小红带的钱数相同,列方程:6x+4=10x-4,解方程,求出每本练习册的价钱,进而求出他们各带的钱数。
【详解】解:设每本练习册价钱是x元。
6x+4=10x-4
6x-6x+4+4=10x-6x-4+4
8=4x
4x÷4=8÷4
x=2
2×6+4
=12+4
=16(元)
小明和小红带同样多的钱去买练习本,小明买了6本后把剩下的4元借给小红,这样正好够小红买10本同样的练习本,他们各带了16元。
【点睛】本题考查方程的实际应用,根据他们各带的钱数相同,利用练习册的本数和练习册的价钱与他们各带钱数的关系,设出未知数,找出相关的量,列方程,解方程。
8. 26.5 36
【分析】根据题意,爸爸穿43码的鞋,即y=43,将其代入y=2x-10中,求出x的值即爸爸的脚长;妈妈的脚长是23厘米,即x=23,将其代入y=2x-10中,求出y值,即妈妈要穿的鞋码。
【详解】由分析可得:
把y=43代入y=2x-10中,得:
y=2x-10
43=2x-10
2x-10=43
2x-10+10=43+10
2x=53
2x÷2=53÷2
x=26.5(厘米)
把x=23代入y=2x-10中,得:
y=2x-10
=2×23-10
=46-10
=36
综上所述:乐乐的爸爸穿43码的鞋,他的脚长是26.5厘米。乐乐的妈妈的脚长是23厘米,她需要穿36码的鞋。
【点睛】本题考查了含有字母的式子的求值,解方程,求值时,要先确定字母等于几,再写出原式,最后把数值代入式子计算。
9.28+45=x
【分析】根据题意可得数量关系是:邮票的张数+邮票比画片少的张数=画片的张数;据此列方程为:28+45=x;据此解题即可。
【详解】解:设画片x张,可得:
28+45=x
所以列方程为:28+45=x。
【点睛】找出等量关系,是解答此题的关键。
10.②④⑤②⑤
【分析】方程是指含有未知数的等式。所以方程必须具备两个条件:①含有未知数;②等式。由此进行选择。
【详解】①x+7.9<16,含有未知数,但不是等式,所以不是方程;②0.23m=4.6,含有未知数且是等式,所以是方程;③55>m÷0.4,含有未知数,但不是等式,所以不是方程;④15×2.4=36,是等式,但不含有未知数,所以不是方程;⑤66-x=38,含有未知数且是等式,所以是方程;则等式有②④⑤,方程有②⑤。
11.×
【分析】设乙原来有x本书,则甲原来有(50-x)本,根据等量关系:甲原来有的本数-8本=乙原来有x本书+8本,列方程解答即可。
【详解】解:设乙原来有x本书,则甲原来有(50-x)本。
50-x-8=x+8
x+x+8=50-8
2x+8=42
2x=34
x=17
50-17=33(本)
所以甲原来有33本,乙原来有17本书。
故答案为:×
【点睛】本题主要考查了列方程解应用题,关键是找等量关系。
12.×
【分析】根据题意,上底、下底和高的长度均为整厘米数,设梯形的上底为x厘米,下底就是2x厘米,高为h厘米,可列方程(x+2x)h÷2=12,根据题意找出符合条件的未知数的值即可。
【详解】解:设设梯形的上底为x厘米,下底就是2x厘米,高为h厘米。
(x+2x)h÷2=12
3xh=24
xh=8
x和h都是整数,则有1×8=8,8×1=8,2×4=8,4×2=8,所以有四组数据。也就是有4种这样不同的直角梯形。
故答案为:×
【点睛】此题主要考查的是梯形的面积公式的应用。注意上下底和高的取值范围。
13.√
【分析】根据等式的性质1:等式两边同时加上或减去同一个数,所得结果还是等式;
【详解】根据分析可知,,方程的两边可以同时加x,方程的解不变。
原题干说法正确。
故答案为:√
【点睛】熟练掌握等式的性质1是解答本题的关键。
14.×
【分析】等式的性质1:将方程左右两边同时加或同一个数,等式仍然成立;等式的性质2:将方程左右两边同时乘同一个数,或除以一个不为0的数,等式仍然成立。据此解答。
【详解】如果,那么根据等式的性质2,将方程左右两边同时乘5,也就是,所以原题干说法错误。
故答案为:×
【点睛】本题主要考查了根据等式的性质2解方程。
15.√
【分析】分别求解这两个方程,得到对应的x的值,然后进行判断。
【详解】
这两个方程的解都是4,所以这两个方程的解相同;
题干阐述正确,答案为:√。
【点睛】当求出第一个方程的解后,可以将其带入第二个方程,根据方程是否成立,如果成立,那么两个方程的解相同,如果不成立,那么两个方程的解不相同。
16.C
【分析】等式的性质1:等式两边同时加上或减去相同的数,等式不变;等式的性质2:等式两边同时乘或除以同一个数(0除外)等式不变,据此逐项分析即可。
【详解】A.2a×10=3b×10,则20a=30b,等式成立;
B.2a-5=3b-5,等式两边同时减去5,等式成立;
C.2a+2=3b+3,等式左边加2,右边也应该加2,但是右边加3,等式不成立;
D.2a÷2=3b÷2,等式两边同时除以2,等式成立。
故答案为:C
【点睛】本题主要考查等式的性质,熟练掌握等式的性质是解题的关键。
17.C
【分析】观察图形可知,丙绳子长度有两部分,一部分是x分米,另一半的长度等于甲绳子的长度减去乙绳子的长度,据此把两边的长度相加即可。
【详解】观察图形可得:
50-35+x
所以,丙绳子的长度是(50-35+x)分米。
故答案为:C
【点睛】读懂题意,正确列式,是解答此题的关键。
18.A
【分析】乙再收集8枚,两人就一样多,则甲的邮票数量-乙再收集的邮票数量=乙原有的邮票数量,据此解答即可。
【详解】甲有枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等,则可列等式。
故答案为:A
【点睛】解决本题的关键是根据题意找出正确的等量关系式。
19.C
【分析】含有未知数的等式叫做方程,据此解答。
【详解】在13b+5>23,x+2.4x=30,45×3=135,1.5m=70,8n-3.6中,x+2.4x=30,1.5m=70都是等式,且含有未知数,所以这两个式子都是方程。
故答案为:C
【点睛】熟练掌握方程的意义是解题的关键。
20.C
【分析】设货车每小时行驶x千米;用货车速度+客车速度,求出两车行驶的速度和,再乘行驶的时间,就是甲、乙两地的距离,据此解方程,解答。
【详解】解:设货车每小时行驶x千米。
4(65+x)=480
4×(65+x)÷4=480÷4
65+x=120
x=120-65
x=55
甲、乙两地相距480千米,客车和货车同时从两地相对开出,经过4小时相遇。已知客车每小时行驶65千米,货车每小时行驶x千米,可列出方程为4(65+x)=480。
故答案为:C
【点睛】本题考查相遇问题,利用速度、时间、路程三者的关系,列方程解答。
21.x=13;x=20.1;
x=5;x=4
【分析】4x+8=60,首先根据等式的性质,两边同时减去8,然后两边同时除以4即可;
(0.7+x)+0.2=21,首先根据等式的性质,两边同时减去0.2,然后两边同时减去0.7即可;
4x-0.6x=17,首先化简,然后根据等式的性质,两边同时除以3.4即可;
1.6x+0.2×8=8,首先根据等式的性质,两边同时减去1.6,然后两边再同时除以1.6即可。
【详解】4x+8=60
解:4x+8-8=60-8
4x=52
4x÷4=52÷4
x=13
0.7+x)+0.2=21
解:0.7+x=21-0.2
0.7+x=20.8
0.7+x-0.7=20.8-0.7
x=20.1
4x-0.6x=17
解:3.4x=17
3.4x÷3.4=17÷3.4
x=5
1.6x+0.2×8=8
解:1.6x+1.6=8
1.6x+1.6-1.6=8-1.6
1.6x=6.4
1.6x÷1.6=6.4÷1.6
x=4
22.4x+5=101;x=24;过程见详解
【分析】每箱是x瓶,一共有4箱,4箱有4x瓶,4x再加上5瓶一共是101瓶,列方程:4x+5=101,解方程,即可解答。
【详解】4x+5=101
解:4x+5-5=101-5
4x=96
4x÷4=96÷4
x=24
23.3y-y=72;y=36
【分析】根据题意可知,桃树有y棵,杏树是桃树的3倍,即杏树是3y棵,杏树比桃树多72棵,列方程:3y-y=72,解方程,即可解答。
【详解】3y-y=72
解:2y=72
2y÷2=72÷2
y=36
24.55元
【分析】设每张桌子的价钱x元,2张桌子的价钱是2x元;一把椅子22元,4把椅子是22×4元;2张桌子和4把椅子一共花了198元,列方程:2x+22×4=198,解方程,即可解答。
【详解】解:设每张桌子的价钱x元。
2x+22×4=198
2x+88=198
2x+88-88=198-88
2x=110
2x÷2=110÷2
x=55
答:每张桌子的价钱是55元。
【点睛】本题考查方程的实际应用,利用买桌子的钱数、买椅子的钱数与总钱数之间的关系,设出未知数,找出相关的量,列方程,解方程。
25.蓝色花区有50公顷,黄色花区有20公顷
【分析】根据题意,这道题的等量关系是:红色花区面积+蓝色花区的面积+黄色花区的面积=150公顷,根据这个等量关系,列方程解答。
【详解】解:设黄色花区的面积约是x公顷。
x+3x-10+80=150
4x+70=150
4x+70-70=150-70
4x=80
4x÷4=80÷4
x=20
蓝色花区=3x-10
=3×20-10
=60-10
=50(公顷)
答:黄色花区的面积为20公顷,蓝色花区的面积为50公顷。
【点睛】本题考查列方程解应用题,解题关键是找出题目中的等量关系:红色花区面积+蓝色花区的面积+黄色花区的面积=150公顷,列方程解答。
26.货包:4.8吨;推进剂:2吨
【分析】设推进剂的质量是x吨,货包的质量约是推进剂的2.4倍,则货包的质量为2.4x吨,货包的质量比推进剂多2.8吨,即货包的质量-推进剂的质量=2.8吨,列方程:2.4x-x=2.8,解方程,求出推进剂的质量,进而求出货包的质量,再进行检验,据此解答。
【详解】解:设推进剂的质量是x吨,则货包质量是2.4x吨。
2.4x-x=2.8
1.4x=2.8
1.4x÷1.4=2.8÷1.4
x=2
货包质量:2×2.4=4.8(吨)
检验:x=2时,
左边:2.4×2-2
=4.8-2
=2.8
右边=2.8
左边=右边,x=2是方程的解。
答:货包的质量是4.8吨,推进剂的质量是2吨。
【点睛】本题考查方程的实际应用,利用推进剂与货包质量之间的关系,设出未知数,找出相关的量,列方程,解方程。
27.小红有96枚;小军有40枚
【分析】根据题意可知,小军收集的邮票数×2.4=小红收集的邮票数,小红收集的邮票数-小军收集的邮票数=56枚,据此设小军收集了x枚邮票,则小红收集了2.4x枚邮票,列方程为2.4x-x=56,然后解出方程即可,进而求出小红的邮票数;最后把结果代入原题,看两人是否相差56枚,小红的邮票数是否是小军的2.4倍。据此解答。
【详解】解:设小军收集了x枚邮票,则小红收集了2.4x枚邮票。
2.4x-x=56
1.4x=56
1.4x÷1.4=56÷1.4
x=40
2.4×40=96(枚)
检验:96-40=56(枚)
96÷40=2.4
答:小红收集了96枚邮票,小军收集了40枚邮票。
【点睛】本题考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
28.0.44平方千米
【分析】设梵蒂冈的面积约是x平方千米。根据题意,梵蒂冈的面积×7-0.18=颐和园的占地面积,据此列方程解答。
【详解】解:设梵蒂冈的面积约是x平方千米。
7x-0.18=2.9
7x=2.9+0.18
7x=3.08
x=3.08÷7
x=0.44
答:梵蒂冈的面积约是0.44平方千米。
【点睛】本题考查列方程解应用题。找出题中的等量关系式是列出方程的关键。
29.3.6亿平方千米
【分析】根据题意,这道题的等量关系是:海洋面积+陆地面积=5.1亿平方千米,根据这个等量关系,列方程解答。
【详解】解:设陆地面积为x亿平方千米,则海洋面积为2.4x亿平方千米。
x+2.4x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=5.1÷3.4
x=1.5
海洋面积:1.5×2.4=3.6(亿平方千米)
答:地球上的海洋面积是3.6亿平方千米。
【点睛】本题考查列方程解应用题,解题关键是找出题目中的等量关系:海洋面积+陆地面积=5.1亿平方千米,列方程解答。
30.五年级去的人数;六年级去的人数;五年级去130人;六年级去156人
【分析】根据题意,五年级去的人数加上六年级去的人数,等于五、六年级共去的286人;又“六年级去的人数是五年级的1.2倍”,设五年级去x人,那么六年级去了1.2x人,根据数量关系“五年级去的人数+六年级去的人数=五、六年级共去的人数”,列方程为:x+1.2x=286;据此求出x的值,用总人数减去五年级人数即可求出六年级的人数。
【详解】解:设五年级去x人,那么六年级去了1.2x人,可得:
x+1.2x=286
2.2x=286
2.2x÷2.2=286÷2.2
x=130
286-130=156(人)
答:五年级去130人,那么六年级去了156人。
数量关系是:
五年级去的人数+六年级去的人数=五、六年级一共的人数
【点睛】理清题意,找出等量关系,设某班去的人数为x,列方程并解方程即可。
31.吉祥药店3200个,大众药店4800个
【分析】大众药店捐赠的口罩数是吉祥药店的1.5倍,设吉祥药店捐赠x个,则大众药店捐赠1.5x个,根据吉祥药店捐赠数量+大众药店捐赠数量=总数量,列方程即可求解。
【详解】解:设吉祥药店捐赠了x个口罩,则大众药店捐赠了1.5x个口罩。
x+1.5x=8000
2.5x=8000
x=8000÷2.5
x=3200
3200×1.5=4800(个)
答:吉祥药店捐赠了3200个口罩,大众药店捐赠了4800个口罩。
【点睛】本题考查列方程解决问题,关键是找出等量关系式。
第一单元《简易方程》
姓名:_________ 班级:_________ 学号:_________
一、填空题(共20分)
1.有两桶油,第一桶油是第二桶油的1.5倍,如果从第一桶中倒入第二桶2千克,两桶油相等,第一桶油原来有()千克。
2.父亲比儿子大30岁,明年父亲的年龄是儿子的3倍,那么今年儿子()岁。
3.4年前,妈妈的年龄正好是小雨年龄的4倍,今年妈妈比小雨大27岁。今年妈妈()岁,小雨()岁。
4.如下图,一张收据被墨汁污损了,每张桌子的价格是()元。
5.甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行。甲每分钟跑270米,乙每分钟跑230米,经过()分甲第一次追上乙。
6.观察下面两组等式,你有什么发现?
17+8=25 17+8-5=25-5 17+8+10=25+10 20×3=60 20×3×4=60×4 20×3÷2=60÷2
发现一:____________________________;
发现二:____________________________。
7.小明和小红带同样多的钱去买练习本,小明买了6本后把剩下的4元借给小红,这样正好够小红买10本同样的练习本,他们各带了()元钱。
8.鞋的尺码通常用“码”和“厘米”作单位,它们之间的换算关系是y=2x-10(y表示鞋的码数,x表厘米数)。乐乐的爸爸穿43码的鞋,他的脚长是()厘米。乐乐的妈妈的脚长是23厘米,她需要穿()码的鞋。
9.看图列方程。
10.在①x+7.9<16,②0.23m=4.6,③55>m÷0.4,④15×2.4=36,⑤66-x=38中,等式有(),方程有()。(填序号)
二、判断题(共10分)
11.甲、乙共有50本书,甲给乙8本,则两人的本数相同,求甲、乙原有书的本数。用方程解,设乙原来有x本书,列方程式x+x+8=50。()
12.一个直角梯形上底是下底的一半,面积是12平方厘米(上下底和直角边的腰长都是整厘米)。这样不同的直角梯形共有3种。()
13.36-x=14,方程的两边可以同时加x,方程的解不变。()
14.如果x÷1.5=4,那么x÷1.5=4×1.5。()
15.3x+18=30和28-2x=20这两个方程的解相同。()
三、选择题(共10分)
16.已知2a=3b(a为非零自然数),根据等式的性质,下面等式( )不成立。
A.20a=30b B.2a-5=3b-5 C.2a+2=3b+3 D.2a÷2=3b÷2
17.如图,有甲、乙、丙三根绳子,丙绳子的长度是( )分米。
A.50-35-x B.50-x+35 C.50-35+x D.35-(50-x)
18.甲有a枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等。下面等式正确的是( )。
A.a-8=15 B.a=15-8 C.a-8=15+8 D.a=15+16
19.在13b+5>23,x+2.4x=30,45×3=135,1.5m=70,8n-3.6中,方程有( )个。
A.3 B.4 C.2 D.1
20.甲、乙两地相距480千米,客车和货车同时从两地相对开出,经过4小时相遇。已知客车每小时行驶65千米,货车每小时行驶x千米,可列出方程为( )。
A.4×65+x=480 B.65+4x=480 C.4(65+x)=480 D.65(4+x)=480
四、计算题(共12分)
21.(6分)解方程。
4x+8=60(0.7+x)+0.2=214x-0.6x=171.6x+0.2×8=8
22.(3分)根据图意列方程解答。(在方框里解答)
23.(3分)看图列方程并解答。
五、解答题(共48分)
24.(6分)如图是一张撕掉一角的发票。请你根发票上的信息,算出每张桌子的价钱。
25.(6分)为了开发城市旅游业,某城市打算建设一处花海基地约150公顷,共种植三种颜色的花,红色花区面积约80公顷,蓝色花区的面积比黄色花区的3倍少10公顷,蓝色、黄色花区的面积各约为多少公顷?(列方程解答)
26.(6分)2021年5月29日,我国成功发射天舟二号货运飞船,飞船此行的主要任务是把航天员和空间站所需的物资送上天,物资包括货包和推进剂两大类,其中货包的质量约是推进剂的2.4倍,货包的质量比推进剂多2.8吨,货包和推进剂的质量各是多少吨?(先列方程解答,再检验。)
27.(6分)
小红和小军各收集了多少枚邮票?(列方程解答,再用“把得数代入原题”的方法检验)
28.(6分)颐和园是我国保存最完整的一座皇家行宫御苑,被誉为“皇家园林博物馆”,占地面积约为2.9平方千米,比世界上面积最小的国家——梵蒂冈的面积的7倍少0.18平方千米。梵蒂冈的面积约是多少平方千米?(列方程解答)
29.(6分)我们的地球是一个美丽的蓝色星球。朵朵同学借助网络查阅了相关资料,了解到地球的表面积一共约5.1亿平方千米。其中海洋面积大约是陆地面积的2.4倍。请你算一算地球上的海洋面积是多少亿平方千米?
30.(6分)同学们参观“第十二届江苏省园艺博览会博览园”。五、六年级共去286人,六年级去的人数是五年级的1.2倍。两个年级各去多少人?(先把数量关系式填写完整,再用方程解答)
( )+( )=五、六年级一共的人数
31.(6分)在2021年度“众志成城,抗击疫情”爱心捐赠活动中,大众药店和吉祥药店一共捐赠了8000个口罩。大众药店捐赠的口罩数是吉祥药店的1.5倍,两个药店各捐赠了多少个口罩?(用方程解)
参考答案
1.12
【分析】设第二桶油原来有x千克,第一桶油是第二桶油的1.5倍,则第一桶油原来有1.5x千克,如果从第一桶中倒入第二桶2千克,两桶油相等,即第一桶油原来的质量-2千克=第二桶油原来的质量+2千克,列方程:1.5x-2=x+2,解方程,即可解答。
【详解】解:设第二桶油原来有x千克,则第一桶油原来有1.5x千克。
1.5x-2=x+2
1.5x-x=2+2
0.5x=4
x=4÷0.5
x=8
1.5×8=12(千克)
有两桶油,第一桶油是第二桶油的1.5倍,如果从第一桶中倒入第二桶2千克,两桶油相等,第一桶油原来有12千克。
【点睛】本题考查方程的实际应用,根据第一桶油原来的质量与第二桶油原来的质量关系,设出未知数,找出相关的量,列方程,解方程。
2.14
【分析】不论经过多少年,父亲和儿子的年龄差不变;设儿子明年x岁,明年父亲的年龄是儿子的3倍,则父亲明年的年龄是3x岁,父亲比儿子大30岁,列方程:3x-x=30,解方程,求出儿子明年的年龄,再减去1,即可求出今年的年龄。
【详解】解:设明年儿子的年龄x岁,明年父亲的年龄3x岁。
3x-x=30
2x=30
2x÷2=30÷2
x=15
15-1=14(岁)
父亲比儿子大30岁,明年父亲的年龄是儿子的3倍,那么今年儿子14岁。
【点睛】本题考查方程的实际应用。根据父亲与儿子的年龄差不变,设出未知数,找出相关的量,列方程,解方程。
3.40 13
【分析】不管过去多少年,妈妈和小雨的年龄差是不会变的;4年前小雨和妈妈相差27岁。设小雨4年前是x岁,妈妈的年龄正好是小雨年龄的4倍,则妈妈的年龄是4x岁,妈妈的年龄-小雨的年龄=27,解方程:4x-x=27,求出小雨4年前的年龄和妈妈4年前的妈妈的年龄,再用小雨4年前的年龄+4,求出小雨今年的年龄;妈妈的年龄+4,求出妈妈今年的年龄,据此解答。
【详解】解:设4年前小雨x岁,则妈妈4x岁。
4x-x=27
3x=27
3x÷3=27÷3
x=9
妈妈4年前的年龄是:9×4=36(岁)
小雨今年年龄:9+4=13(岁)
妈妈今年年龄:36+4=40(岁)
4年前,妈妈的年龄正好是小雨年龄的4倍,今年妈妈比小雨大27岁。今年妈妈40岁,小雨13岁。
【点睛】本题考查方程的实际应用,利用小雨与妈妈年龄之间的关系,设出未知数,找出相关的量,列方程,解方程;关键明确年龄差是不变的。
4.67
【分析】根据单价×数量=总价,可得椅子的单价×椅子的数量+桌子的单价×桌子的数量=284元,设每张桌子的价格是x元,据此列方程为:2x+6×25=284,然后解出方程即可。
【详解】解:设每张桌子的价格是x元。
2x+6×25=284
2x+150=284
2x+150-150=284-150
2x=134
2x÷2=134÷2
x=67
每张桌子的价格是67元。
【点睛】本题可用列方程解决问题,找到相应的数量关系式是解答本题的关键。
5.10
【分析】根据题意可知,甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,同向而行,相当于两人在直线上相距400米,从同一地点出发,同向而行,根据速度差×追及时间=路程差,设经过x分甲第一次追上乙,列方程为(270-230)x=400,然后解出方程即可。
【详解】解:设经过x分甲第一次追上乙。
(270-230)x=400
40x=400
40x÷40=400÷40
x=10
经过10分甲第一次追上乙。
【点睛】本题可用列方程解决问题,找到相应的数量关系式是解答本题的关键。
6.在加法算式中,两边同时加上或减去同一个数,所得结果仍然是等式在乘法算式中,两边同时乘或除以同一个数(0除外),所得结果仍然是等式
【分析】通过观察可知:在等式的两边同时加或减同一个数,等式仍然成立;在等式两边同时乘或除以同一个不为零的数,等式仍然成立。据此解答。
【详解】发现一:在加法算式中,两边同时加上或减去同一个数,所得结果仍然是等式。
发现二:在乘法算式中,两边同时乘或除以同一个数(0除外),所得结果仍然是等式
【点睛】从等式中找到、发现规律是解答的关键。
7.16
【分析】设每本练习册价钱是x元,小明买了6本,花了6x元;小红买了10本,花了10x元。小明买了6本后把剩下的4元借给小红,小明买6本练习册的钱数+4元=小明带的钱数;小红买10本练习册的钱数-4元=小红带的钱数,小明和小红带的钱数相同,列方程:6x+4=10x-4,解方程,求出每本练习册的价钱,进而求出他们各带的钱数。
【详解】解:设每本练习册价钱是x元。
6x+4=10x-4
6x-6x+4+4=10x-6x-4+4
8=4x
4x÷4=8÷4
x=2
2×6+4
=12+4
=16(元)
小明和小红带同样多的钱去买练习本,小明买了6本后把剩下的4元借给小红,这样正好够小红买10本同样的练习本,他们各带了16元。
【点睛】本题考查方程的实际应用,根据他们各带的钱数相同,利用练习册的本数和练习册的价钱与他们各带钱数的关系,设出未知数,找出相关的量,列方程,解方程。
8. 26.5 36
【分析】根据题意,爸爸穿43码的鞋,即y=43,将其代入y=2x-10中,求出x的值即爸爸的脚长;妈妈的脚长是23厘米,即x=23,将其代入y=2x-10中,求出y值,即妈妈要穿的鞋码。
【详解】由分析可得:
把y=43代入y=2x-10中,得:
y=2x-10
43=2x-10
2x-10=43
2x-10+10=43+10
2x=53
2x÷2=53÷2
x=26.5(厘米)
把x=23代入y=2x-10中,得:
y=2x-10
=2×23-10
=46-10
=36
综上所述:乐乐的爸爸穿43码的鞋,他的脚长是26.5厘米。乐乐的妈妈的脚长是23厘米,她需要穿36码的鞋。
【点睛】本题考查了含有字母的式子的求值,解方程,求值时,要先确定字母等于几,再写出原式,最后把数值代入式子计算。
9.28+45=x
【分析】根据题意可得数量关系是:邮票的张数+邮票比画片少的张数=画片的张数;据此列方程为:28+45=x;据此解题即可。
【详解】解:设画片x张,可得:
28+45=x
所以列方程为:28+45=x。
【点睛】找出等量关系,是解答此题的关键。
10.②④⑤②⑤
【分析】方程是指含有未知数的等式。所以方程必须具备两个条件:①含有未知数;②等式。由此进行选择。
【详解】①x+7.9<16,含有未知数,但不是等式,所以不是方程;②0.23m=4.6,含有未知数且是等式,所以是方程;③55>m÷0.4,含有未知数,但不是等式,所以不是方程;④15×2.4=36,是等式,但不含有未知数,所以不是方程;⑤66-x=38,含有未知数且是等式,所以是方程;则等式有②④⑤,方程有②⑤。
11.×
【分析】设乙原来有x本书,则甲原来有(50-x)本,根据等量关系:甲原来有的本数-8本=乙原来有x本书+8本,列方程解答即可。
【详解】解:设乙原来有x本书,则甲原来有(50-x)本。
50-x-8=x+8
x+x+8=50-8
2x+8=42
2x=34
x=17
50-17=33(本)
所以甲原来有33本,乙原来有17本书。
故答案为:×
【点睛】本题主要考查了列方程解应用题,关键是找等量关系。
12.×
【分析】根据题意,上底、下底和高的长度均为整厘米数,设梯形的上底为x厘米,下底就是2x厘米,高为h厘米,可列方程(x+2x)h÷2=12,根据题意找出符合条件的未知数的值即可。
【详解】解:设设梯形的上底为x厘米,下底就是2x厘米,高为h厘米。
(x+2x)h÷2=12
3xh=24
xh=8
x和h都是整数,则有1×8=8,8×1=8,2×4=8,4×2=8,所以有四组数据。也就是有4种这样不同的直角梯形。
故答案为:×
【点睛】此题主要考查的是梯形的面积公式的应用。注意上下底和高的取值范围。
13.√
【分析】根据等式的性质1:等式两边同时加上或减去同一个数,所得结果还是等式;
【详解】根据分析可知,,方程的两边可以同时加x,方程的解不变。
原题干说法正确。
故答案为:√
【点睛】熟练掌握等式的性质1是解答本题的关键。
14.×
【分析】等式的性质1:将方程左右两边同时加或同一个数,等式仍然成立;等式的性质2:将方程左右两边同时乘同一个数,或除以一个不为0的数,等式仍然成立。据此解答。
【详解】如果,那么根据等式的性质2,将方程左右两边同时乘5,也就是,所以原题干说法错误。
故答案为:×
【点睛】本题主要考查了根据等式的性质2解方程。
15.√
【分析】分别求解这两个方程,得到对应的x的值,然后进行判断。
【详解】
这两个方程的解都是4,所以这两个方程的解相同;
题干阐述正确,答案为:√。
【点睛】当求出第一个方程的解后,可以将其带入第二个方程,根据方程是否成立,如果成立,那么两个方程的解相同,如果不成立,那么两个方程的解不相同。
16.C
【分析】等式的性质1:等式两边同时加上或减去相同的数,等式不变;等式的性质2:等式两边同时乘或除以同一个数(0除外)等式不变,据此逐项分析即可。
【详解】A.2a×10=3b×10,则20a=30b,等式成立;
B.2a-5=3b-5,等式两边同时减去5,等式成立;
C.2a+2=3b+3,等式左边加2,右边也应该加2,但是右边加3,等式不成立;
D.2a÷2=3b÷2,等式两边同时除以2,等式成立。
故答案为:C
【点睛】本题主要考查等式的性质,熟练掌握等式的性质是解题的关键。
17.C
【分析】观察图形可知,丙绳子长度有两部分,一部分是x分米,另一半的长度等于甲绳子的长度减去乙绳子的长度,据此把两边的长度相加即可。
【详解】观察图形可得:
50-35+x
所以,丙绳子的长度是(50-35+x)分米。
故答案为:C
【点睛】读懂题意,正确列式,是解答此题的关键。
18.A
【分析】乙再收集8枚,两人就一样多,则甲的邮票数量-乙再收集的邮票数量=乙原有的邮票数量,据此解答即可。
【详解】甲有枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等,则可列等式。
故答案为:A
【点睛】解决本题的关键是根据题意找出正确的等量关系式。
19.C
【分析】含有未知数的等式叫做方程,据此解答。
【详解】在13b+5>23,x+2.4x=30,45×3=135,1.5m=70,8n-3.6中,x+2.4x=30,1.5m=70都是等式,且含有未知数,所以这两个式子都是方程。
故答案为:C
【点睛】熟练掌握方程的意义是解题的关键。
20.C
【分析】设货车每小时行驶x千米;用货车速度+客车速度,求出两车行驶的速度和,再乘行驶的时间,就是甲、乙两地的距离,据此解方程,解答。
【详解】解:设货车每小时行驶x千米。
4(65+x)=480
4×(65+x)÷4=480÷4
65+x=120
x=120-65
x=55
甲、乙两地相距480千米,客车和货车同时从两地相对开出,经过4小时相遇。已知客车每小时行驶65千米,货车每小时行驶x千米,可列出方程为4(65+x)=480。
故答案为:C
【点睛】本题考查相遇问题,利用速度、时间、路程三者的关系,列方程解答。
21.x=13;x=20.1;
x=5;x=4
【分析】4x+8=60,首先根据等式的性质,两边同时减去8,然后两边同时除以4即可;
(0.7+x)+0.2=21,首先根据等式的性质,两边同时减去0.2,然后两边同时减去0.7即可;
4x-0.6x=17,首先化简,然后根据等式的性质,两边同时除以3.4即可;
1.6x+0.2×8=8,首先根据等式的性质,两边同时减去1.6,然后两边再同时除以1.6即可。
【详解】4x+8=60
解:4x+8-8=60-8
4x=52
4x÷4=52÷4
x=13
0.7+x)+0.2=21
解:0.7+x=21-0.2
0.7+x=20.8
0.7+x-0.7=20.8-0.7
x=20.1
4x-0.6x=17
解:3.4x=17
3.4x÷3.4=17÷3.4
x=5
1.6x+0.2×8=8
解:1.6x+1.6=8
1.6x+1.6-1.6=8-1.6
1.6x=6.4
1.6x÷1.6=6.4÷1.6
x=4
22.4x+5=101;x=24;过程见详解
【分析】每箱是x瓶,一共有4箱,4箱有4x瓶,4x再加上5瓶一共是101瓶,列方程:4x+5=101,解方程,即可解答。
【详解】4x+5=101
解:4x+5-5=101-5
4x=96
4x÷4=96÷4
x=24
23.3y-y=72;y=36
【分析】根据题意可知,桃树有y棵,杏树是桃树的3倍,即杏树是3y棵,杏树比桃树多72棵,列方程:3y-y=72,解方程,即可解答。
【详解】3y-y=72
解:2y=72
2y÷2=72÷2
y=36
24.55元
【分析】设每张桌子的价钱x元,2张桌子的价钱是2x元;一把椅子22元,4把椅子是22×4元;2张桌子和4把椅子一共花了198元,列方程:2x+22×4=198,解方程,即可解答。
【详解】解:设每张桌子的价钱x元。
2x+22×4=198
2x+88=198
2x+88-88=198-88
2x=110
2x÷2=110÷2
x=55
答:每张桌子的价钱是55元。
【点睛】本题考查方程的实际应用,利用买桌子的钱数、买椅子的钱数与总钱数之间的关系,设出未知数,找出相关的量,列方程,解方程。
25.蓝色花区有50公顷,黄色花区有20公顷
【分析】根据题意,这道题的等量关系是:红色花区面积+蓝色花区的面积+黄色花区的面积=150公顷,根据这个等量关系,列方程解答。
【详解】解:设黄色花区的面积约是x公顷。
x+3x-10+80=150
4x+70=150
4x+70-70=150-70
4x=80
4x÷4=80÷4
x=20
蓝色花区=3x-10
=3×20-10
=60-10
=50(公顷)
答:黄色花区的面积为20公顷,蓝色花区的面积为50公顷。
【点睛】本题考查列方程解应用题,解题关键是找出题目中的等量关系:红色花区面积+蓝色花区的面积+黄色花区的面积=150公顷,列方程解答。
26.货包:4.8吨;推进剂:2吨
【分析】设推进剂的质量是x吨,货包的质量约是推进剂的2.4倍,则货包的质量为2.4x吨,货包的质量比推进剂多2.8吨,即货包的质量-推进剂的质量=2.8吨,列方程:2.4x-x=2.8,解方程,求出推进剂的质量,进而求出货包的质量,再进行检验,据此解答。
【详解】解:设推进剂的质量是x吨,则货包质量是2.4x吨。
2.4x-x=2.8
1.4x=2.8
1.4x÷1.4=2.8÷1.4
x=2
货包质量:2×2.4=4.8(吨)
检验:x=2时,
左边:2.4×2-2
=4.8-2
=2.8
右边=2.8
左边=右边,x=2是方程的解。
答:货包的质量是4.8吨,推进剂的质量是2吨。
【点睛】本题考查方程的实际应用,利用推进剂与货包质量之间的关系,设出未知数,找出相关的量,列方程,解方程。
27.小红有96枚;小军有40枚
【分析】根据题意可知,小军收集的邮票数×2.4=小红收集的邮票数,小红收集的邮票数-小军收集的邮票数=56枚,据此设小军收集了x枚邮票,则小红收集了2.4x枚邮票,列方程为2.4x-x=56,然后解出方程即可,进而求出小红的邮票数;最后把结果代入原题,看两人是否相差56枚,小红的邮票数是否是小军的2.4倍。据此解答。
【详解】解:设小军收集了x枚邮票,则小红收集了2.4x枚邮票。
2.4x-x=56
1.4x=56
1.4x÷1.4=56÷1.4
x=40
2.4×40=96(枚)
检验:96-40=56(枚)
96÷40=2.4
答:小红收集了96枚邮票,小军收集了40枚邮票。
【点睛】本题考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
28.0.44平方千米
【分析】设梵蒂冈的面积约是x平方千米。根据题意,梵蒂冈的面积×7-0.18=颐和园的占地面积,据此列方程解答。
【详解】解:设梵蒂冈的面积约是x平方千米。
7x-0.18=2.9
7x=2.9+0.18
7x=3.08
x=3.08÷7
x=0.44
答:梵蒂冈的面积约是0.44平方千米。
【点睛】本题考查列方程解应用题。找出题中的等量关系式是列出方程的关键。
29.3.6亿平方千米
【分析】根据题意,这道题的等量关系是:海洋面积+陆地面积=5.1亿平方千米,根据这个等量关系,列方程解答。
【详解】解:设陆地面积为x亿平方千米,则海洋面积为2.4x亿平方千米。
x+2.4x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=5.1÷3.4
x=1.5
海洋面积:1.5×2.4=3.6(亿平方千米)
答:地球上的海洋面积是3.6亿平方千米。
【点睛】本题考查列方程解应用题,解题关键是找出题目中的等量关系:海洋面积+陆地面积=5.1亿平方千米,列方程解答。
30.五年级去的人数;六年级去的人数;五年级去130人;六年级去156人
【分析】根据题意,五年级去的人数加上六年级去的人数,等于五、六年级共去的286人;又“六年级去的人数是五年级的1.2倍”,设五年级去x人,那么六年级去了1.2x人,根据数量关系“五年级去的人数+六年级去的人数=五、六年级共去的人数”,列方程为:x+1.2x=286;据此求出x的值,用总人数减去五年级人数即可求出六年级的人数。
【详解】解:设五年级去x人,那么六年级去了1.2x人,可得:
x+1.2x=286
2.2x=286
2.2x÷2.2=286÷2.2
x=130
286-130=156(人)
答:五年级去130人,那么六年级去了156人。
数量关系是:
五年级去的人数+六年级去的人数=五、六年级一共的人数
【点睛】理清题意,找出等量关系,设某班去的人数为x,列方程并解方程即可。
31.吉祥药店3200个,大众药店4800个
【分析】大众药店捐赠的口罩数是吉祥药店的1.5倍,设吉祥药店捐赠x个,则大众药店捐赠1.5x个,根据吉祥药店捐赠数量+大众药店捐赠数量=总数量,列方程即可求解。
【详解】解:设吉祥药店捐赠了x个口罩,则大众药店捐赠了1.5x个口罩。
x+1.5x=8000
2.5x=8000
x=8000÷2.5
x=3200
3200×1.5=4800(个)
答:吉祥药店捐赠了3200个口罩,大众药店捐赠了4800个口罩。
【点睛】本题考查列方程解决问题,关键是找出等量关系式。
