第四单元:比例(单元复习课件)-人教版六年级数学下册(共44张PPT)
文档属性
| 名称 | 第四单元:比例(单元复习课件)-人教版六年级数学下册(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-20 09:38:11 | ||
图片预览







文档简介
(共44张PPT)
比例
复习专题
人教版六年级数学下册
1
比例的意义和基本性质
2
正比例和反比例
3
比例的应用
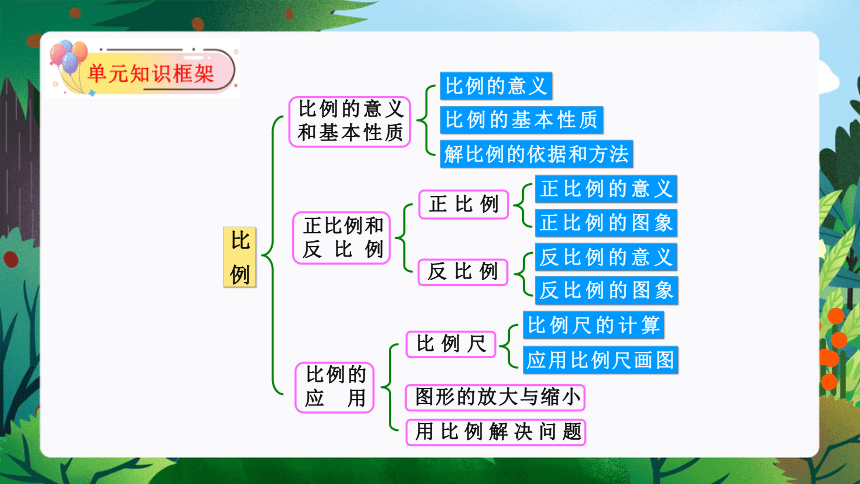
比例
比例的意义和基本性质
比例的意义
比例的基本性质
解比例的依据和方法
正比例
正比例的意义
正比例的图象
反比例
反比例的意义
反比例的图象
比例尺
比例尺的计算
应用比例尺画图
图形的放大与缩小
用比例解决问题
正比例和反比例
比例的应用
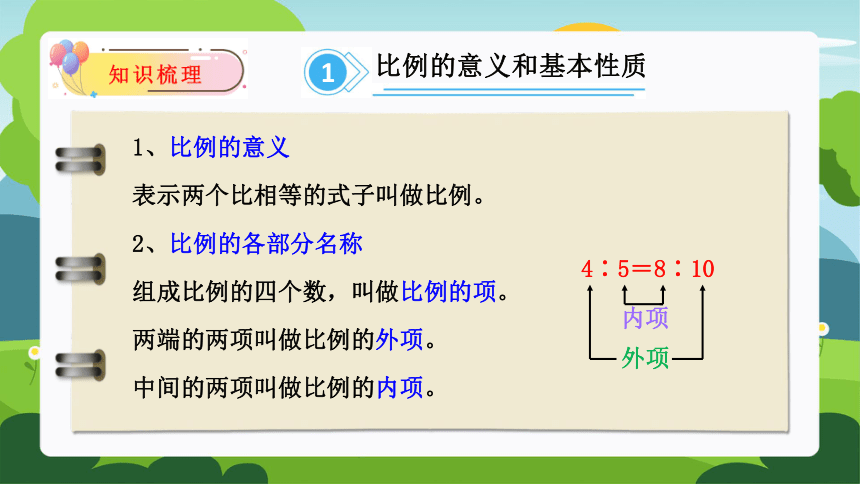
1、比例的意义
表示两个比相等的式子叫做比例。
2、比例的各部分名称
组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
4∶5=8∶10
内项
外项
1
比例的意义和基本性质
【例1】下面各组比中,能与∶组成比例的是( )。
A、2∶3 B、3∶2 C、 ∶
判断两个比能否可以组成比例,可以看它们的比值是否相等。比值相等,就能组成比例;比值不相等,就不能组成比例。
∶= ÷= ×3=
选项A: 2∶3= ≠,A错。
选项B: 3∶2= ,B正确。
选项C: ∶ = ÷= ×2= ≠,C错。
组成比例的两个比既可以写成带比号的形式,也可以写成分数的形式,但读法相同。
B
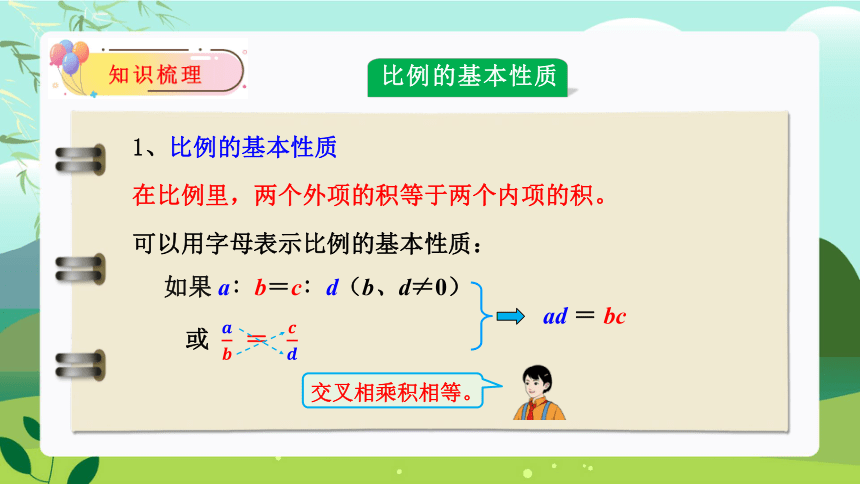
1、比例的基本性质
在比例里,两个外项的积等于两个内项的积。
可以用字母表示比例的基本性质:
比例的基本性质
如果 a∶b=c∶d(b、d≠0)
ad = bc
或 =
交叉相乘积相等。
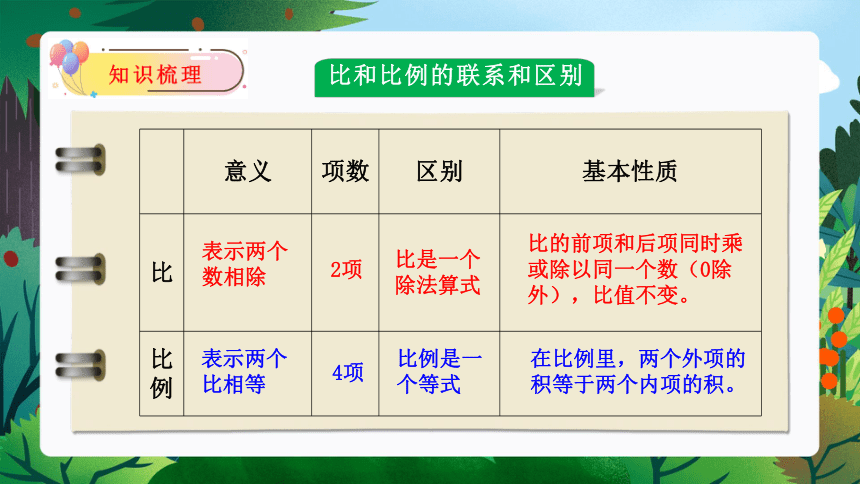
比和比例的联系和区别
意义 项数 区别 基本性质
比
比例
表示两个数相除
表示两个比相等
2项
4项
比是一个除法算式
比例是一个等式
比的前项和后项同时乘或除以同一个数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
【例2】在一个比例中,已知两个外项的积是900,如果一个内项是36,那么另一个内项是( )。
A、35 B、25 C、15
根据比例的基本性质:两个外项的积等于两个内项的积。已知两个外项的积,用外项积除以其中一个内项,就能得到另一个内项。
900÷36=25,则另一个内项是25,故答案选B。
B
【例3】如果A×=B÷(其中A、B均不为0),那么A∶B=( )∶( )。
因为A×=B÷
A×=B×
所以A∶B = ∶ =( ×12)∶(×12)=15∶8
15
8
【例4】在比例24∶16=18∶12中,如果将第一个比的前项减去6,那么第二个比的后项应该加上( )才能使比例成立。
在比例24∶16=18∶12中,设第二个比的后项应该加上x才能使比例成立,
(24-6)∶16=18∶(12+x)
化简可得:18∶16=18∶(12+x)
因为比例的内项积等于外项积,所以16×18=18×(12+x)
x=4
因此,第二个比的后项应该加上4才能使比例成立。
4
1、求比例中的未知项,叫做解比例。
2、解比例的依据:比例的基本性质。
3、解比例的方法
可以根据比例的基本性质将原式转化成学过的方程,再解方程;也可以先将原式进行整理计算,再转化成学过的方程来解。
解比例
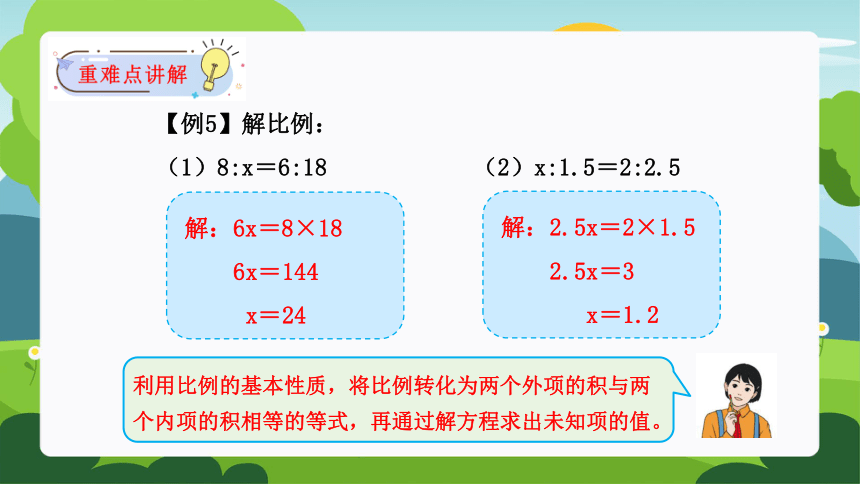
【例5】解比例:
(1)8:x=6:18 (2)x:1.5=2:2.5
解:6x=8×18
6x=144
x=24
利用比例的基本性质,将比例转化为两个外项的积与两个内项的积相等的等式,再通过解方程求出未知项的值。
解:2.5x=2×1.5
2.5x=3
x=1.2
【例5】解比例:
(3) :x= : (4) :x= :9
解:x= ×
x=
x= ×
x=
解:x= ×9
x=7
x=7×
x=
解比例时,先分清内外项。一般把x写在等号的左边,这样便于解方程。
【例5】解比例:
(5) = (6) =
解:0.6x=12×0.5
0.6x=6
x=6÷0.6
x=10
可以利用“交叉相乘积相等”将原式转化成学过的方程来解。
解:22×3x=6×11
66x=66
x=66÷66
x=1
2
正比例和反比例
正比例
1、两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
2、如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以表示为 。
3、正比例的图象
如果把成正比例关系的两个量中相对应的数都看作是一个数对,在方格纸上把写这些数对相对应的点连起来,形成一条射线;
反之,该射线上的每一个点对应的就是正比例关系中两个相关联的量的一组具体值。
正比例
【例6】辩一辩,对的打√,错的打×。
(1)长方形的周长和宽成正比例。( )
(2)如果三角形的底不变,那么它的面积和高成正比例。( )
(3)正方形的周长和边长成正比。( )
(1)两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。因为长方形的长=-宽,周长与宽不成比值,所以它们不成正比例,故(1)错误。
×
【例6】辩一辩,对的打√,错的打×。
(1)长方形的周长和宽成正比例。( )
(2)如果三角形的底不变,那么它的面积和高成正比例。( )
(3)正方形的周长和边长成正比。( )
(2)因为三角形的底=×2,当底不变时,面积与高的比值是一定的,所以它们成正比例,故(2)正确。
×
√
【例6】辩一辩,对的打√,错的打×。
(1)长方形的周长和宽成正比例。( )
(2)如果三角形的底不变,那么它的面积和高成正比例。( )
(3)正方形的周长和边长成正比。( )
(3)由正方形的周长=边长×4得:4=。因为4是定值,也就是正方形的周长和边长的商一定,所以正方形的周长和边长成正比。故(3)是正确的。
×
√
√
【例7】数学老师购买的作业本的数量和总价如下表所示。
(1)根据表格中的数量关系,把表格填写完整。
数量/本 1 3 5 7 ( ) …
总价/元 2 6 ( ) 14 18 …
根据“单价×数量=总价”可以求出:5×2=10(元);
根据“数量=总价÷单价”可以求出:18÷2=9(本)。
10
9
【例7】数学老师购买的作业本的数
量和总价如下表所示。
(2)在右图中把本子数量与总价所
对应的点描出来,并连线。
【例7】数学老师购买的作业本的数
量和总价如下表所示。
(3)作业本的总价与数量成什么关
系?请说明理由。
(3)根据图像可以知道,总价与数量成正比例关系。因为总价÷数量=单价,单价一定,所以总价和数量成正比例。
反比例
1、反比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
2、如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以表示为xy=k。
3、反比例的图象
反比例关系也可以用图象来表示,如果把成反比例关系的两个量中相对应的数都看作是一个数对,在方格纸上把写这些数对相对应的点连起来,会形成一条光滑的曲线;
反之,该曲线上的每一个点对应的就是反比例关系中两个相关联的量的一组具体值。
【例8】辩一辩,对的打√,错的打×。
(1)当圆柱的体积一定时,它的底面积和高成反比例。( )
(2)当工作总量一定时,已经完成的工作量和剩下的工作量成反比例。( )
(3)用双手将一个平行四边形框架的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高成反比例。( )
(1)两种相关联的量,如果这两种量中相对应的两个数乘积一定时,这两种量成反比例。因为根据圆柱的体积公=底面积×高,圆柱的体积一定,即乘积一定,那么它的底面积和高成反比例,故(1)正确。
√
【例8】辩一辩,对的打√,错的打×。
(1)当圆柱的体积一定时,它的底面积和高成反比例。( )
(2)当工作总量一定时,已经完成的工作量和剩下的工作量成反比例。( )
(3)用双手将一个平行四边形框架的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高成反比例。( )
(2)工作总量=已经完成的工作量+剩下的工作量,已经完成的工作量和剩下的工作量的和是一定的,不是乘积一定,不符合反比例的定义,所以它们不成比例,故(2)错误。
√
×
【例8】辩一辩,对的打√,错的打×。
(1)当圆柱的体积一定时,它的底面积和高成反比例。( )
(2)当工作总量一定时,已经完成的工作量和剩下的工作量成反比例。( )
(3)用双手将一个平行四边形框架的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高成反比例。( )
(3)这个变化过程中平行四边形的底是不变,高改变,根据平行四边形的底=平行四边形的面积÷高,底不变,则平行四边形的面积和高的比值不变,所以平行四边形的面积和高成正比例。故(3)错误。
√
×
×
【例9】运输队为农场运送一批水果。
(1)如果要一次性把所有的水果全部运出,车辆的载重量与所需车辆的数量如下表。请你把表格填写完整。
每辆车载重量/吨 1.5 2 2.4 ( )
车辆数量/辆 8 6 ( ) 4
(1)由“水果总质量=每辆车载重量×车辆数量”可得水果总质量:1.5×8=12(吨);由“车辆数量=水果总质量÷每辆车载重量”得:12÷2.4=5(辆)。
由“车辆数量=水果总质量÷每辆车载重量”得:12÷4=3(吨)。
5
3
【例9】运输队为农场运送一批水果。
(2)每辆车的载重量和所需车辆的数量成什么比例?为什么?
每辆车载重量/吨 1.5 2 2.4 (3)
车辆数量/辆 8 6 (5) 4
(2)1.5×8=2×6=12(吨),即每辆车的载重量×所需辆数=水果总吨数(一定),所以每辆车的载重量和所需车辆的数量成反比例关系。
【例9】运输队为农场运送一批水果。
(3)如果每辆车的载重量是4.8吨,派2辆车一次性可以运送完这批水果吗?
每辆车载重量/吨 1.5 2 2.4 (3)
车辆数量/辆 8 6 (5) 4
(3)4.8×2=9.6(吨)
9.6<12
答:派2辆车来一次性不可以运送完这批水果。
正比例与反比例的异同点
正比例 反比例
相同点 不同点
都是两种相关联的量;
一种量变化,另一种量也随着变化。
1、相对应的两个数的比值一定。
2、一种量扩大(或缩小),另一种量也随着扩大(或缩小);
1、相对应的两个数的乘积一定。
2、一种量扩大(或缩小),另一种量反而缩小(或扩大);
3
比例的应用
1、一幅图的图上距离与实际距离的比,叫做这幅图的比例尺。
图上距离∶实际距离=比例尺 或 =比例尺
2、按照表现形式分,比例尺有数值比例尺和线段比例尺两种,两种比例尺可以互相转化。
按将实际距离缩小还是放大分,可以分为缩小比例尺和放大比例尺。
3、应用比例尺画图:
①根据实际距离与纸张的大小确定平面图的比例尺;
②根据比例尺求出图上距离;
③根据图上距离画出相应的平面图;
④标明平面图的名称和比例尺。
4、比例尺是一个比,它表示图上距离和实际距离的关系,因此不能带计量单位。
【例10】一块玩具积木长1.2cm,画在一张图纸上长30cm。这幅图的比例尺是( )。
图上距离∶实际距离=比例尺
30cm:1.2cm
=300:12
=(300÷12):(12÷12)
=25:1
数值比例尺是一个比,它表示图上距离和实际距离的关系,因此不能带计量单位。
25:1
【例11】把线段比例尺 改写成数值比例尺是( )。
A、 B、 C、
进行有关比例尺的计算时,一定要注意单位是否统一。
50千米=5000000厘米
图上距离∶实际距离=比例尺
1:5000000=
A
【例12】一块长方形的空地,长160米,宽60米,用1:2000的比例尺画出这块空地的平面图。
160米=16000厘米
60米=6000厘米
图上距离=实际距离×比例尺
16000×=8(厘米)
6000×=3(厘米)
8厘米
3厘米
1、图形按一定的比放大或缩小后,只是图形的大小发生了变化,图形原有的形状没变化。
2、把图形按比放大或缩小,就是把图形的每一条边都按比放大或缩小。
3、形放大或缩小后,形状不变,相对应的角的度数也不变。
图形的放大与缩小
【例13】把一个长方形长27厘米,宽15厘米,按1:3缩小后,得到的新的长方形的面积是( )平方厘米。
按照1:3缩小后,长和宽都变成原来的
27× =9(厘米)
15× =5(厘米)
长方形的面积=长×宽
9×5=45(平方厘米)
45
用比例解决问题
【例14】妈妈买了8kg西瓜和5kg葡萄,买这两种水果所花的钱数一样多,西瓜和葡萄的单价之比是( );如果西瓜的单价是6元,那么葡萄的单价是( )元。
(1)分别把买两种水果的钱看成单位“1”,则西瓜和葡萄的单价之比为西瓜:葡萄=5:8。
(2)解:设葡萄的单价是x元。
=
5x=8×6
5x=48
x=9.6
5:8
9.6
【例15】东东想测量一根电线杆的高度,量得电线杆的影长是4.5米,同时有一根长4米的标杆直立在地面上,量得此时的影长是1.2米,这根电线杆高多少米?(用比例解决)
电线杆的高度:电线杆的影长=标杆的高度:标杆的影长
解:设这根电线杆高x米。
x:4.5=4:1.2
1.2x=4.5×4
1.2x=18
x=18÷1.2
x=15
答:这根电线杆高15米。
1、下列选项中,( )中的两种量成正比例。
A、当总价不变时,单价和数量
B、正方体的表面积与它的棱长
C、8m=6n
2、在一个比例中,已知两个内项互为倒数,且其中一个外项是12.5,另一个外项是( )。
C
0.08
3、填表。
比例尺 图上距离 实际距离
1∶300 6.9米
1∶50000 2.8千米
1∶200000 6厘米
2.3厘米
5.6厘米
12千米
4、刘叔叔有一辆汽车,下表是这辆汽
车的车辆行驶过程中的数据。
(1)在右图中把汽车行驶路程与耗油
量所对应的点描出来,并连线。
(2)汽车的耗油量和行驶路程成( )比例关系。
正
每一份努力,都将在学习中得到最好的回报。加油!
比例
复习专题
人教版六年级数学下册
1
比例的意义和基本性质
2
正比例和反比例
3
比例的应用
比例
比例的意义和基本性质
比例的意义
比例的基本性质
解比例的依据和方法
正比例
正比例的意义
正比例的图象
反比例
反比例的意义
反比例的图象
比例尺
比例尺的计算
应用比例尺画图
图形的放大与缩小
用比例解决问题
正比例和反比例
比例的应用
1、比例的意义
表示两个比相等的式子叫做比例。
2、比例的各部分名称
组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项。
中间的两项叫做比例的内项。
4∶5=8∶10
内项
外项
1
比例的意义和基本性质
【例1】下面各组比中,能与∶组成比例的是( )。
A、2∶3 B、3∶2 C、 ∶
判断两个比能否可以组成比例,可以看它们的比值是否相等。比值相等,就能组成比例;比值不相等,就不能组成比例。
∶= ÷= ×3=
选项A: 2∶3= ≠,A错。
选项B: 3∶2= ,B正确。
选项C: ∶ = ÷= ×2= ≠,C错。
组成比例的两个比既可以写成带比号的形式,也可以写成分数的形式,但读法相同。
B
1、比例的基本性质
在比例里,两个外项的积等于两个内项的积。
可以用字母表示比例的基本性质:
比例的基本性质
如果 a∶b=c∶d(b、d≠0)
ad = bc
或 =
交叉相乘积相等。
比和比例的联系和区别
意义 项数 区别 基本性质
比
比例
表示两个数相除
表示两个比相等
2项
4项
比是一个除法算式
比例是一个等式
比的前项和后项同时乘或除以同一个数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
【例2】在一个比例中,已知两个外项的积是900,如果一个内项是36,那么另一个内项是( )。
A、35 B、25 C、15
根据比例的基本性质:两个外项的积等于两个内项的积。已知两个外项的积,用外项积除以其中一个内项,就能得到另一个内项。
900÷36=25,则另一个内项是25,故答案选B。
B
【例3】如果A×=B÷(其中A、B均不为0),那么A∶B=( )∶( )。
因为A×=B÷
A×=B×
所以A∶B = ∶ =( ×12)∶(×12)=15∶8
15
8
【例4】在比例24∶16=18∶12中,如果将第一个比的前项减去6,那么第二个比的后项应该加上( )才能使比例成立。
在比例24∶16=18∶12中,设第二个比的后项应该加上x才能使比例成立,
(24-6)∶16=18∶(12+x)
化简可得:18∶16=18∶(12+x)
因为比例的内项积等于外项积,所以16×18=18×(12+x)
x=4
因此,第二个比的后项应该加上4才能使比例成立。
4
1、求比例中的未知项,叫做解比例。
2、解比例的依据:比例的基本性质。
3、解比例的方法
可以根据比例的基本性质将原式转化成学过的方程,再解方程;也可以先将原式进行整理计算,再转化成学过的方程来解。
解比例
【例5】解比例:
(1)8:x=6:18 (2)x:1.5=2:2.5
解:6x=8×18
6x=144
x=24
利用比例的基本性质,将比例转化为两个外项的积与两个内项的积相等的等式,再通过解方程求出未知项的值。
解:2.5x=2×1.5
2.5x=3
x=1.2
【例5】解比例:
(3) :x= : (4) :x= :9
解:x= ×
x=
x= ×
x=
解:x= ×9
x=7
x=7×
x=
解比例时,先分清内外项。一般把x写在等号的左边,这样便于解方程。
【例5】解比例:
(5) = (6) =
解:0.6x=12×0.5
0.6x=6
x=6÷0.6
x=10
可以利用“交叉相乘积相等”将原式转化成学过的方程来解。
解:22×3x=6×11
66x=66
x=66÷66
x=1
2
正比例和反比例
正比例
1、两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
2、如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以表示为 。
3、正比例的图象
如果把成正比例关系的两个量中相对应的数都看作是一个数对,在方格纸上把写这些数对相对应的点连起来,形成一条射线;
反之,该射线上的每一个点对应的就是正比例关系中两个相关联的量的一组具体值。
正比例
【例6】辩一辩,对的打√,错的打×。
(1)长方形的周长和宽成正比例。( )
(2)如果三角形的底不变,那么它的面积和高成正比例。( )
(3)正方形的周长和边长成正比。( )
(1)两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。因为长方形的长=-宽,周长与宽不成比值,所以它们不成正比例,故(1)错误。
×
【例6】辩一辩,对的打√,错的打×。
(1)长方形的周长和宽成正比例。( )
(2)如果三角形的底不变,那么它的面积和高成正比例。( )
(3)正方形的周长和边长成正比。( )
(2)因为三角形的底=×2,当底不变时,面积与高的比值是一定的,所以它们成正比例,故(2)正确。
×
√
【例6】辩一辩,对的打√,错的打×。
(1)长方形的周长和宽成正比例。( )
(2)如果三角形的底不变,那么它的面积和高成正比例。( )
(3)正方形的周长和边长成正比。( )
(3)由正方形的周长=边长×4得:4=。因为4是定值,也就是正方形的周长和边长的商一定,所以正方形的周长和边长成正比。故(3)是正确的。
×
√
√
【例7】数学老师购买的作业本的数量和总价如下表所示。
(1)根据表格中的数量关系,把表格填写完整。
数量/本 1 3 5 7 ( ) …
总价/元 2 6 ( ) 14 18 …
根据“单价×数量=总价”可以求出:5×2=10(元);
根据“数量=总价÷单价”可以求出:18÷2=9(本)。
10
9
【例7】数学老师购买的作业本的数
量和总价如下表所示。
(2)在右图中把本子数量与总价所
对应的点描出来,并连线。
【例7】数学老师购买的作业本的数
量和总价如下表所示。
(3)作业本的总价与数量成什么关
系?请说明理由。
(3)根据图像可以知道,总价与数量成正比例关系。因为总价÷数量=单价,单价一定,所以总价和数量成正比例。
反比例
1、反比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
2、如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以表示为xy=k。
3、反比例的图象
反比例关系也可以用图象来表示,如果把成反比例关系的两个量中相对应的数都看作是一个数对,在方格纸上把写这些数对相对应的点连起来,会形成一条光滑的曲线;
反之,该曲线上的每一个点对应的就是反比例关系中两个相关联的量的一组具体值。
【例8】辩一辩,对的打√,错的打×。
(1)当圆柱的体积一定时,它的底面积和高成反比例。( )
(2)当工作总量一定时,已经完成的工作量和剩下的工作量成反比例。( )
(3)用双手将一个平行四边形框架的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高成反比例。( )
(1)两种相关联的量,如果这两种量中相对应的两个数乘积一定时,这两种量成反比例。因为根据圆柱的体积公=底面积×高,圆柱的体积一定,即乘积一定,那么它的底面积和高成反比例,故(1)正确。
√
【例8】辩一辩,对的打√,错的打×。
(1)当圆柱的体积一定时,它的底面积和高成反比例。( )
(2)当工作总量一定时,已经完成的工作量和剩下的工作量成反比例。( )
(3)用双手将一个平行四边形框架的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高成反比例。( )
(2)工作总量=已经完成的工作量+剩下的工作量,已经完成的工作量和剩下的工作量的和是一定的,不是乘积一定,不符合反比例的定义,所以它们不成比例,故(2)错误。
√
×
【例8】辩一辩,对的打√,错的打×。
(1)当圆柱的体积一定时,它的底面积和高成反比例。( )
(2)当工作总量一定时,已经完成的工作量和剩下的工作量成反比例。( )
(3)用双手将一个平行四边形框架的两个对角慢慢向两边拉动,这个变化过程中平行四边形的面积和高成反比例。( )
(3)这个变化过程中平行四边形的底是不变,高改变,根据平行四边形的底=平行四边形的面积÷高,底不变,则平行四边形的面积和高的比值不变,所以平行四边形的面积和高成正比例。故(3)错误。
√
×
×
【例9】运输队为农场运送一批水果。
(1)如果要一次性把所有的水果全部运出,车辆的载重量与所需车辆的数量如下表。请你把表格填写完整。
每辆车载重量/吨 1.5 2 2.4 ( )
车辆数量/辆 8 6 ( ) 4
(1)由“水果总质量=每辆车载重量×车辆数量”可得水果总质量:1.5×8=12(吨);由“车辆数量=水果总质量÷每辆车载重量”得:12÷2.4=5(辆)。
由“车辆数量=水果总质量÷每辆车载重量”得:12÷4=3(吨)。
5
3
【例9】运输队为农场运送一批水果。
(2)每辆车的载重量和所需车辆的数量成什么比例?为什么?
每辆车载重量/吨 1.5 2 2.4 (3)
车辆数量/辆 8 6 (5) 4
(2)1.5×8=2×6=12(吨),即每辆车的载重量×所需辆数=水果总吨数(一定),所以每辆车的载重量和所需车辆的数量成反比例关系。
【例9】运输队为农场运送一批水果。
(3)如果每辆车的载重量是4.8吨,派2辆车一次性可以运送完这批水果吗?
每辆车载重量/吨 1.5 2 2.4 (3)
车辆数量/辆 8 6 (5) 4
(3)4.8×2=9.6(吨)
9.6<12
答:派2辆车来一次性不可以运送完这批水果。
正比例与反比例的异同点
正比例 反比例
相同点 不同点
都是两种相关联的量;
一种量变化,另一种量也随着变化。
1、相对应的两个数的比值一定。
2、一种量扩大(或缩小),另一种量也随着扩大(或缩小);
1、相对应的两个数的乘积一定。
2、一种量扩大(或缩小),另一种量反而缩小(或扩大);
3
比例的应用
1、一幅图的图上距离与实际距离的比,叫做这幅图的比例尺。
图上距离∶实际距离=比例尺 或 =比例尺
2、按照表现形式分,比例尺有数值比例尺和线段比例尺两种,两种比例尺可以互相转化。
按将实际距离缩小还是放大分,可以分为缩小比例尺和放大比例尺。
3、应用比例尺画图:
①根据实际距离与纸张的大小确定平面图的比例尺;
②根据比例尺求出图上距离;
③根据图上距离画出相应的平面图;
④标明平面图的名称和比例尺。
4、比例尺是一个比,它表示图上距离和实际距离的关系,因此不能带计量单位。
【例10】一块玩具积木长1.2cm,画在一张图纸上长30cm。这幅图的比例尺是( )。
图上距离∶实际距离=比例尺
30cm:1.2cm
=300:12
=(300÷12):(12÷12)
=25:1
数值比例尺是一个比,它表示图上距离和实际距离的关系,因此不能带计量单位。
25:1
【例11】把线段比例尺 改写成数值比例尺是( )。
A、 B、 C、
进行有关比例尺的计算时,一定要注意单位是否统一。
50千米=5000000厘米
图上距离∶实际距离=比例尺
1:5000000=
A
【例12】一块长方形的空地,长160米,宽60米,用1:2000的比例尺画出这块空地的平面图。
160米=16000厘米
60米=6000厘米
图上距离=实际距离×比例尺
16000×=8(厘米)
6000×=3(厘米)
8厘米
3厘米
1、图形按一定的比放大或缩小后,只是图形的大小发生了变化,图形原有的形状没变化。
2、把图形按比放大或缩小,就是把图形的每一条边都按比放大或缩小。
3、形放大或缩小后,形状不变,相对应的角的度数也不变。
图形的放大与缩小
【例13】把一个长方形长27厘米,宽15厘米,按1:3缩小后,得到的新的长方形的面积是( )平方厘米。
按照1:3缩小后,长和宽都变成原来的
27× =9(厘米)
15× =5(厘米)
长方形的面积=长×宽
9×5=45(平方厘米)
45
用比例解决问题
【例14】妈妈买了8kg西瓜和5kg葡萄,买这两种水果所花的钱数一样多,西瓜和葡萄的单价之比是( );如果西瓜的单价是6元,那么葡萄的单价是( )元。
(1)分别把买两种水果的钱看成单位“1”,则西瓜和葡萄的单价之比为西瓜:葡萄=5:8。
(2)解:设葡萄的单价是x元。
=
5x=8×6
5x=48
x=9.6
5:8
9.6
【例15】东东想测量一根电线杆的高度,量得电线杆的影长是4.5米,同时有一根长4米的标杆直立在地面上,量得此时的影长是1.2米,这根电线杆高多少米?(用比例解决)
电线杆的高度:电线杆的影长=标杆的高度:标杆的影长
解:设这根电线杆高x米。
x:4.5=4:1.2
1.2x=4.5×4
1.2x=18
x=18÷1.2
x=15
答:这根电线杆高15米。
1、下列选项中,( )中的两种量成正比例。
A、当总价不变时,单价和数量
B、正方体的表面积与它的棱长
C、8m=6n
2、在一个比例中,已知两个内项互为倒数,且其中一个外项是12.5,另一个外项是( )。
C
0.08
3、填表。
比例尺 图上距离 实际距离
1∶300 6.9米
1∶50000 2.8千米
1∶200000 6厘米
2.3厘米
5.6厘米
12千米
4、刘叔叔有一辆汽车,下表是这辆汽
车的车辆行驶过程中的数据。
(1)在右图中把汽车行驶路程与耗油
量所对应的点描出来,并连线。
(2)汽车的耗油量和行驶路程成( )比例关系。
正
每一份努力,都将在学习中得到最好的回报。加油!
