江苏省丰县刘王楼初级中学苏科版八年级数学下册9.5.1 三角形的内角和课件(共23张ppt)
文档属性
| 名称 | 江苏省丰县刘王楼初级中学苏科版八年级数学下册9.5.1 三角形的内角和课件(共23张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 450.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 00:00:00 | ||
图片预览





文档简介
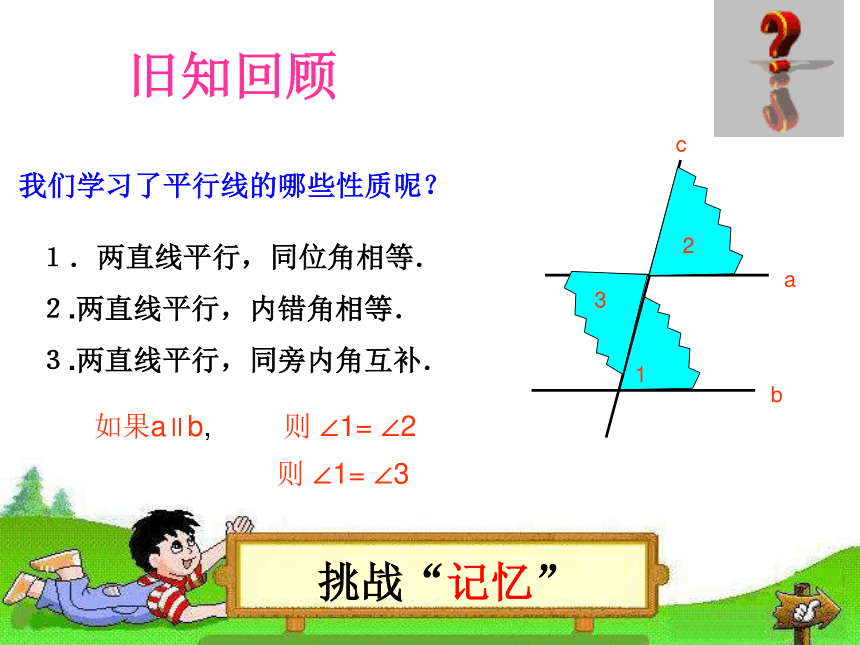
课件23张PPT。1旧知回顾我们学习了平行线的哪些性质呢?1.两直线平行,同位角相等.
2.两直线平行,内错角相等.
3.两直线平行,同旁内角互补.abc1如果a∥b,则 ∠1= ∠232则 ∠1= ∠31问题同学们,你们知道其中的道理吗?
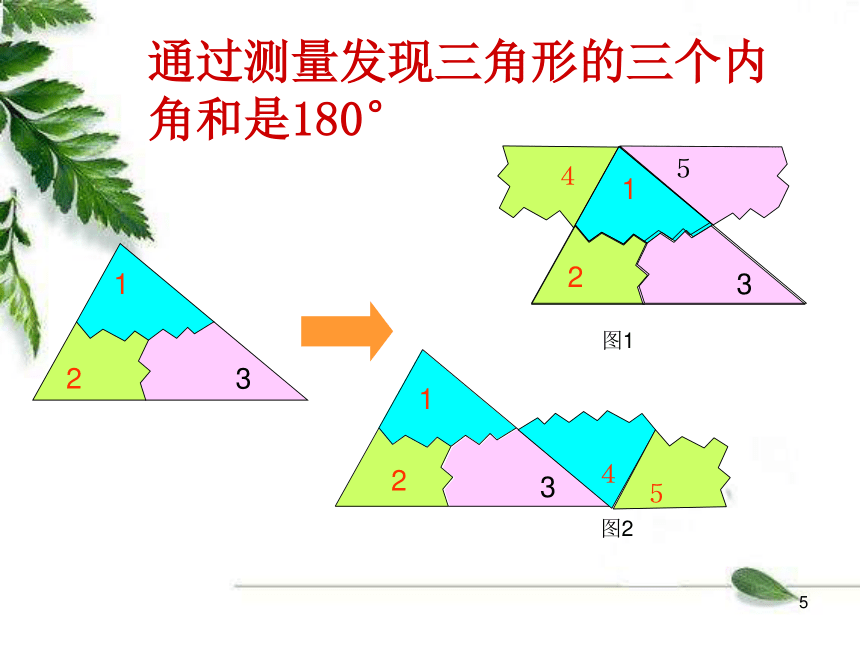
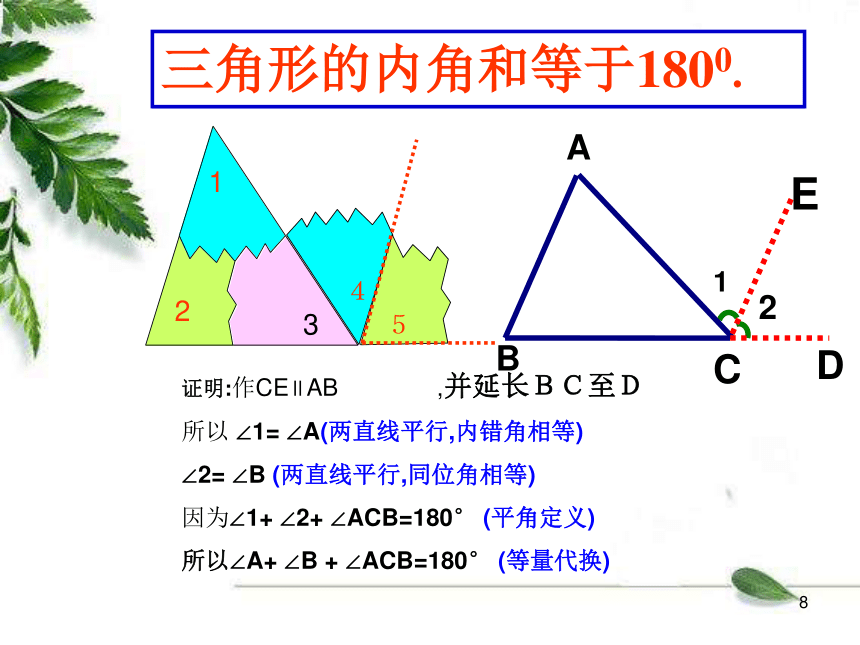
三角形的内角和与外角和1你有什么办法可以探究它呢?方法一:通过具体的度量,验证三角形的内角和 方法二:剪拼法.把三个角拼在一起试试看?1通过测量发现三角形的三个内角和是180°图1图242531542123311三角形的三个内角和是180° 刚才拼角的过程你能想出证明的方法吗?图1图224352514123131
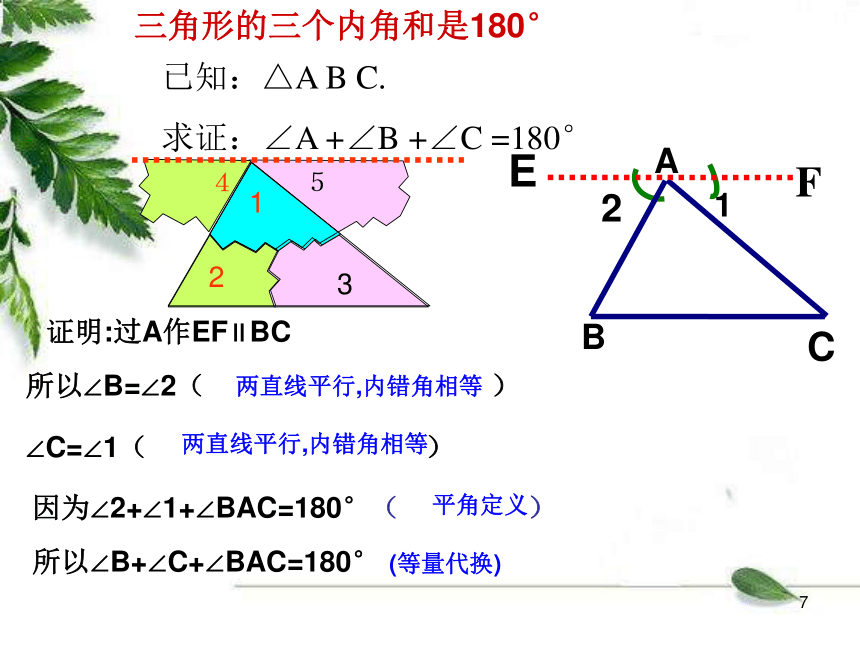
证明:过A作EF∥BC所以∠B=∠2( )
∠C=∠1( )因为∠2+∠1+∠BAC=180°( )所以∠B+∠C+∠BAC=180° (等量代换)平角定义两直线平行,内错角相等两直线平行,内错角相等已知:△A B C.
求证:∠A +∠B +∠C =180°三角形的三个内角和是180°123541三角形的内角和等于1800.证明:作CE∥AB ,并延长BC至D
所以 ∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
因为∠1+ ∠2+ ∠ACB=180° (平角定义)
所以∠A+ ∠B + ∠ACB=180° (等量代换)12345三角形的内角和性质文字语言:三角形的内角和等于180°
符号语言:
因为∠A、∠B、∠C是△ABC的三个内角
所以∠A+∠B+∠C=180°(三角形的内角和等于180°)结论在△ABC中,已知∠B=35°,∠C=55°,求∠A的度数。
解:因为∠A +∠B+∠C=180°
(三角形的内角和等于180°)
由∠B=35°,∠C=55°
得∠A =90°
例题11新知应用比一比,赛一赛看哪一组做得又对又快!(1)在△ABC中,∠A=35°,∠ B=43 ° ,
则∠ C= .
(2) 在△ABC中,∠C +∠B =140°则∠A=____。
(3)在△ABC中, ∠A=40 ° ∠A=2∠B,
则∠C=____。102 °40 °120°例题2在△ABC中,∠A的度数是∠B的度数的3倍,
∠C比 ∠B 大15°, 求∠A、 ∠B 、∠C的度数.在△ABC中,∠A:∠B:∠C=1:2:3,求∠A 、∠B 、∠C的度数。
解:根据题意,可设∠A、∠B、∠C的度数分别为x、2x、3x
因为∠A+∠B+∠C=180°
(三角形的内角和等于180°)
即 x+2x+3x=180
解得:x=30
所以∠A=30°、∠B=60°、∠C=90°例题3在△ABC中,∠B=50°,∠ACB=60°
CD是∠ACB的角平分线,求∠BDC的度数。练习解:因为CD是∠ACB的角平分线, ∠ACB=60°
所以
因为∠A +∠B+∠C=180°
(三角形的内角和等于180°)
由∠B=50°
得∠BDC =100°三个角都是锐角的三角形叫做锐角三角形.如图(1)有一个角是直角的三角形叫
做直角三角形.如图(2)有一个角是钝角的三角形
叫钝角三角形.如图(3)锐角三角形和钝角三角形合称斜三角形议一议一个三角形的三个内角中,最多有几个直角?最多有几个钝角?三角形按角分类三角形锐角三角形直角三角形钝角三角形 在一个三角形中,最多有几个锐角?几个直角?几个钝角?直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC,在直角三角形中,夹直角的两边叫作直角边两边相等的三角形叫作等腰三角形,两条直角边相等的直角三角形叫作等腰直角三角形直角的对边叫作斜边,直角边直角边斜边由三角形内角和性质易得:把△ABC的一边BC延长,得到∠ACD,像这样,三角形一边与另一边的延长线组成的角,叫作三角形的外角,三角形的外角与内角之间有什么样的关系呢?你能讲出道理吗?ABC对外角∠ACD而言,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.三角形的一个外角大于任何一个和它不相邻的内角.由三角形内角和等于180o,可以得到下面的结论:三角形的一个外角等于和它不相邻的两个内角的和. 由又∠A, ∠B, ∠ACB为三角形内角ABC与三角形的一个内角相邻 的外角有多少个?它们之间有什么关系?ABCF2相等如图,对于△ABC每一个内角取它的一个外角,如∠ACE,∠BAF,∠CBD,量一量这三个外角的大小,猜一猜任意三角形的三个外角的和是多少?ABCDFE360°三角形的三个外角和等于360o因为 ∠ACE=∠1+∠2,(为什么?) ∠BAF=∠2+∠3,(为什么?)∠CBD=∠1+∠3,(为什么?)所以 ∠ACE+∠BAF+∠CBD=2(∠1+∠2+∠3)=2×180o=360oABCDFE312练习:如图,已知∠DAC=100o, ∠ABC=30o,求∠ACB的值.ABCD100°30°∠CAB=180°-∠DAC=180°-100°=80°∠ACB=180°-∠CAB-∠B=180°-80°-30°=70°
2.两直线平行,内错角相等.
3.两直线平行,同旁内角互补.abc1如果a∥b,则 ∠1= ∠232则 ∠1= ∠31问题同学们,你们知道其中的道理吗?
三角形的内角和与外角和1你有什么办法可以探究它呢?方法一:通过具体的度量,验证三角形的内角和 方法二:剪拼法.把三个角拼在一起试试看?1通过测量发现三角形的三个内角和是180°图1图242531542123311三角形的三个内角和是180° 刚才拼角的过程你能想出证明的方法吗?图1图224352514123131
证明:过A作EF∥BC所以∠B=∠2( )
∠C=∠1( )因为∠2+∠1+∠BAC=180°( )所以∠B+∠C+∠BAC=180° (等量代换)平角定义两直线平行,内错角相等两直线平行,内错角相等已知:△A B C.
求证:∠A +∠B +∠C =180°三角形的三个内角和是180°123541三角形的内角和等于1800.证明:作CE∥AB ,并延长BC至D
所以 ∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
因为∠1+ ∠2+ ∠ACB=180° (平角定义)
所以∠A+ ∠B + ∠ACB=180° (等量代换)12345三角形的内角和性质文字语言:三角形的内角和等于180°
符号语言:
因为∠A、∠B、∠C是△ABC的三个内角
所以∠A+∠B+∠C=180°(三角形的内角和等于180°)结论在△ABC中,已知∠B=35°,∠C=55°,求∠A的度数。
解:因为∠A +∠B+∠C=180°
(三角形的内角和等于180°)
由∠B=35°,∠C=55°
得∠A =90°
例题11新知应用比一比,赛一赛看哪一组做得又对又快!(1)在△ABC中,∠A=35°,∠ B=43 ° ,
则∠ C= .
(2) 在△ABC中,∠C +∠B =140°则∠A=____。
(3)在△ABC中, ∠A=40 ° ∠A=2∠B,
则∠C=____。102 °40 °120°例题2在△ABC中,∠A的度数是∠B的度数的3倍,
∠C比 ∠B 大15°, 求∠A、 ∠B 、∠C的度数.在△ABC中,∠A:∠B:∠C=1:2:3,求∠A 、∠B 、∠C的度数。
解:根据题意,可设∠A、∠B、∠C的度数分别为x、2x、3x
因为∠A+∠B+∠C=180°
(三角形的内角和等于180°)
即 x+2x+3x=180
解得:x=30
所以∠A=30°、∠B=60°、∠C=90°例题3在△ABC中,∠B=50°,∠ACB=60°
CD是∠ACB的角平分线,求∠BDC的度数。练习解:因为CD是∠ACB的角平分线, ∠ACB=60°
所以
因为∠A +∠B+∠C=180°
(三角形的内角和等于180°)
由∠B=50°
得∠BDC =100°三个角都是锐角的三角形叫做锐角三角形.如图(1)有一个角是直角的三角形叫
做直角三角形.如图(2)有一个角是钝角的三角形
叫钝角三角形.如图(3)锐角三角形和钝角三角形合称斜三角形议一议一个三角形的三个内角中,最多有几个直角?最多有几个钝角?三角形按角分类三角形锐角三角形直角三角形钝角三角形 在一个三角形中,最多有几个锐角?几个直角?几个钝角?直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC,在直角三角形中,夹直角的两边叫作直角边两边相等的三角形叫作等腰三角形,两条直角边相等的直角三角形叫作等腰直角三角形直角的对边叫作斜边,直角边直角边斜边由三角形内角和性质易得:把△ABC的一边BC延长,得到∠ACD,像这样,三角形一边与另一边的延长线组成的角,叫作三角形的外角,三角形的外角与内角之间有什么样的关系呢?你能讲出道理吗?ABC对外角∠ACD而言,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.三角形的一个外角大于任何一个和它不相邻的内角.由三角形内角和等于180o,可以得到下面的结论:三角形的一个外角等于和它不相邻的两个内角的和. 由又∠A, ∠B, ∠ACB为三角形内角ABC与三角形的一个内角相邻 的外角有多少个?它们之间有什么关系?ABCF2相等如图,对于△ABC每一个内角取它的一个外角,如∠ACE,∠BAF,∠CBD,量一量这三个外角的大小,猜一猜任意三角形的三个外角的和是多少?ABCDFE360°三角形的三个外角和等于360o因为 ∠ACE=∠1+∠2,(为什么?) ∠BAF=∠2+∠3,(为什么?)∠CBD=∠1+∠3,(为什么?)所以 ∠ACE+∠BAF+∠CBD=2(∠1+∠2+∠3)=2×180o=360oABCDFE312练习:如图,已知∠DAC=100o, ∠ABC=30o,求∠ACB的值.ABCD100°30°∠CAB=180°-∠DAC=180°-100°=80°∠ACB=180°-∠CAB-∠B=180°-80°-30°=70°
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
