【多媒体导学案】人教版数学九年级上册第24章第1课时《与圆有关的概念》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第1课时《与圆有关的概念》(教师版) |  | |
| 格式 | zip | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 10:06:13 | ||
图片预览




文档简介
一、学习目标 1.认识圆,掌握圆的特征;2.理解同圆中直径与半径的关系;3.学会用圆规正确画圆.
二、知识回顾 1.说出生活中与圆有关的物体. 车轮、碗底、柱子、方向盘、硬币等. 思考:车轮为什么做成圆形? 车轮设计成圆的,可以让车轮轴(圆心)到地面的距离不变,不至于颠簸. 2.小花、小强、小彬三人相邀掷飞镖比赛. ( http: / / www.21cnjy.com )他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜.如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好? ( http: / / www.21cnjy.com )
三、新知讲解 1.圆的有关概念①圆的定义有两种表达形式:如图,在平面内,线段OA绕它固定的一个端点O旋转一周,另一端点A所形成的图形叫做圆,记作“”,读作“圆O”.固定的端点O叫做 圆心 ,线段OA叫做 半径 . ( http: / / www.21cnjy.com )圆心为O,半径为r的圆可以看成是是平面内所有到定点O的距离等于定长r的点的集合.②连接圆上任意两点的线段叫做 弦 .③通过圆心的弦叫做 直径 .④圆上任意两点间的部分叫做圆弧,简称 弧 .⑤圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做 半圆 .⑥大于半圆的弧叫做 优弧 .⑦小于半圆的弧叫做 劣弧 .⑧能够重合的两个圆叫做等圆. 在同圆或等圆中,能够互相重合的弧叫做 等弧 .2.圆的内部、外部圆的内部可以看作是到圆心的距离 小于半径 的点的集合.圆的外部可以看作是到圆心的距离 大于半径 的点的集合.
四、典例探究 扫一扫,有惊喜哦!1.根据圆的基本概念判断说法正误【例1】(2015春 张掖校级月考)有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是( )A.1 B.2 C.3 D.4总结:与圆有关的概念我们要注意以下几点:1.确定圆的条件是圆心与半径.2.直径是弦,直径是圆内最长的弦.弦不一定是直径,只有过圆心的弦才是直径.3.半圆是弧,但弧不一定是半圆.练1.(2014秋 梁子湖区期末)车轮要做成圆形,实际上就是根据圆的特征( )A.圆上各点到圆心的距离相等 B.直径是圆中最长的弦C.同弧所对的圆周角相等 D.圆是中心对称图形2.求证正方形四个顶点共圆【例2】正方形ABCD的对角线AC,BD相交于点O.求证:A,B,C,D四个点在以O为圆心的同一个圆上. ( http: / / www.21cnjy.com )总结:证明四点共圆,关键是说明这四点到圆心的距离相等.常见的四点共圆的情况如下:矩形的四个顶点共圆;正方形的四个顶点共圆;有公共斜边的两个直角三角形的四个顶点共圆;对角互补的凸四边形的四个顶点共圆.练2.已知矩形的两边长分别为6和8,则矩形的四个顶点在以_____为圆心,以______为半径的圆上.3.利用同圆半径相等求解【例3】(2014秋 中山月考)如图,在R ( http: / / www.21cnjy.com )t△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A=_______. ( http: / / www.21cnjy.com )总结:根据同圆半径相等可得出等腰三角形,根据等腰三角形两底角相等,或结合三角形外角的性质、三角形内角和定理即可求得角的度数.练3.(2011秋 江宁区校级期中)如图,BD=OD,∠AOC=114°,求∠AOD的度数. ( http: / / www.21cnjy.com )
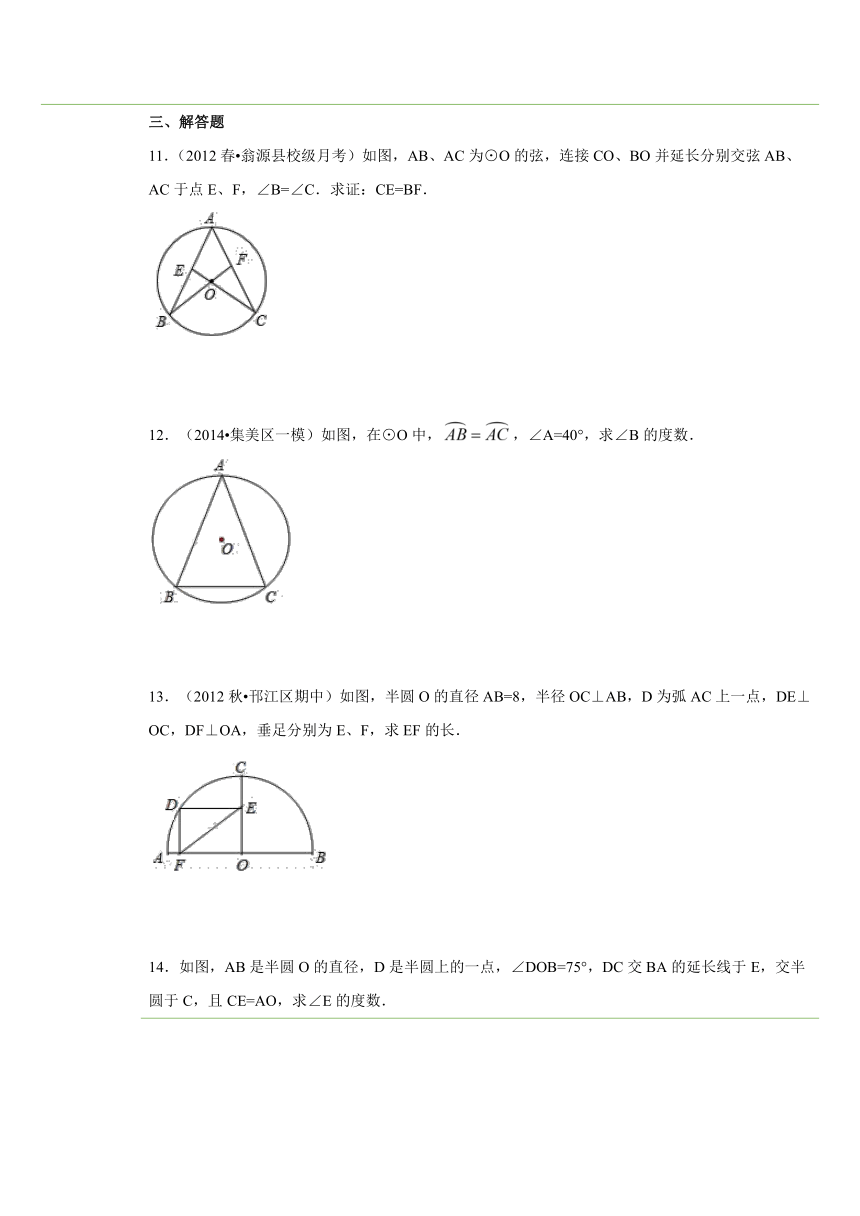
五、课后小测 一、选择题1.(2014 长宁区一模)下列说法中,结论错误的是( )A.直径相等的两个圆是等圆B.长度相等的两条弧是等弧C.圆中最长的弦是直径D.一条弦把圆分成两条弧,这两条弧可能是等弧2.(2014秋 泰州校级期中)下列说法中,结论错误的是( )A.直径相等的两个圆是等圆B.三角形的外心是这个三角形三条角平分线的交点C.圆中最长的弦是直径D.一条弦把圆分成两条弧,这两条弧可能是等弧3.把圆的半径缩小到原来的,那么圆的面积缩小到原来的( )A. B. C. D.4.半径为5的圆的一条弦长不可能是( )A.3 B.5 C.10 D.125.(2015 茂名模拟)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( ) ( http: / / www.21cnjy.com )A.80° B.70° C.60° D.40°6.(2010秋 张家港市校级月考)过圆上一点可以作出圆的最长弦的条数为( )A.1条 B.2条 C.3条 D.无数条二、填空题7.(2014秋 天河区校级期中)如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为______cm. ( http: / / www.21cnjy.com )8.(2014秋 丹阳市校级月考)如图,在 ( http: / / www.21cnjy.com )⊙O中,点A、O、D和点B、O、C分别在一条直线上,图中共有________条弦,它们分别是______________________. ( http: / / www.21cnjy.com )9.(2010秋 邗江区期 ( http: / / www.21cnjy.com )末)已知⊙O的半径为5,圆心在坐标原点,位于第二象限的该圆上的一点P的横坐标和纵坐标均为整数.则点P的坐标为________.(写出一个即可)10.圆的半径为3,则弦AB长度的取值范围是_______.三、解答题11.(2012春 翁源县校级月考)如 ( http: / / www.21cnjy.com )图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF. ( http: / / www.21cnjy.com )12.(2014 集美区一模)如图,在⊙O中,,∠A=40°,求∠B的度数. ( http: / / www.21cnjy.com )13.(2012秋 邗江区期中)如 ( http: / / www.21cnjy.com )图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长. ( http: / / www.21cnjy.com )14.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据弦的定义、弧的定义、以及确定圆的条件即可解决.
解:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的 ( http: / / www.21cnjy.com )任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
【点评】本题考查弦与直径的区别,弧与半圆的区别,及确定圆的条件,不要将弦与直径、弧与半圆混淆.
练1.【解析】根据车轮的特点和功能进行解答.
解:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选A.
【点评】本题考查了对圆的基本认识,即墨经所说:圆,一中同长也,属于基础知识,难度较小.
【例2】【解析】要说明几个点共圆的问题,只需证明这几个点到同一个点的距离相等,此题可以充分运用正方形的性质进行证明.
证明:∵四边形ABCD为正方形,
∴OA=OC=AC,OB=OD=BD,AC=BD.
∴OA=OB=OC=OD.
∴ A,B,C,D四个点在以O为圆心的同一个圆上.
【点评】此题考查了点和圆的位置关系,要掌握证明几点共圆的方法:即证明这些点到同一个点的距离相等.
练2.【解析】因矩形的对角线是圆的直径.所以两条对角线的交点为圆心,半径为5.
解:在矩形ABCD中,根据勾股定理求得:AC=BD==10,则OA=OC=OB=OD=5.
如图,
( http: / / www.21cnjy.com )
∵∠ABC=∠ADC=90°,
∴AC是直径,即矩形ABCD的四个顶点在以对角线交点为圆心,以5为半径的圆上.
故答案是:对角线交点;5.
【点评】本题考查了点与圆的位置关系.根据圆周角定理推知AC为直径是解题的关键.
【例3】【解析】由半径相等得CB=CD,则∠B=∠CDB,在根据三角形内角和计算出∠B=(180°﹣∠BCD)=70°,然后利用互余计算∠A的度数.
解:∵CB=CD,
∴∠B=∠CDB,
∵∠B+∠CDB+∠BCD=180°,
∴∠B=(180°﹣∠BCD)=(180°﹣40°)=70°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=20°.
故答案为20°.
【点评】本题考查了同圆半径相等.
练3.【解析】设∠B=x,根据等腰三角形的性 ( http: / / www.21cnjy.com )质,由BD=OD得∠DOB=∠B=x,再根据三角形外角性质得∠ADO=2x,则∠A=∠ADO=2x,然后根据三角形外角性质得2x+x=114°,解得x=38°,最后利用三角形内角和定理计算∠AOD的度数.
解:设∠B=x,
∵BD=OD,
∴∠DOB=∠B=x,
∴∠ADO=∠DOB+∠B=2x,
∵OA=OD,
∴∠A=∠ADO=2x,
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°,
∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
课后小测答案:
一、选择题
1.【解析】利用圆的有关定义进行判断后利用排除法即可得到正确的答案;
解:A、直径相等的两个圆是等圆,正确,不符合题意;
B、长度相等的两条弧圆周角不一定相等,它们不一定是等弧,原题的说法是错误的,符合题意;
C、圆中最长的弦是直径,正确,不符合题意;
D、一条直径把圆分成两条弧,这两条弧是等弧,正确,不符合题意,
故选:B.
【点评】本题考查了圆的认识,了解圆中有关的定义及性质是解答本题的关键.
2.【解析】根据等圆的定义对A进行判断;根据三角形外心的定义对B进行判断;根据直径的定义对C进行判断;根据等弧的定义对D进行判断.
解:A、直径相等的两个圆是等圆,所以A选项的说法正确;
B、三角形的外心是这个三角形三边的中垂线的交点,所以B选项的说法错误;
C、圆中最长的弦是直径,所以C选项的说法正确;
D、一条直径弦圆分成两条弧,这两条弧是等弧,所以D选项的说法正确.
故选:B.
【点评】本题考查了圆的认识:与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了矩形的性质.
3.【解析】因为圆的面积公式是:s=πr2,所以圆的面积和此圆半径的平方有关系,设出原圆的半径,再表示出现在圆的半径代入公式求解即可.
解:设原来的圆的半径为r,则面积s1=πr2,
∴缩小到原来的后,s2=π(r)2=πr2,
∴.
故选:D.
【点评】本题考查了圆的面积公式,在公式中:圆的面积和半径的平方成正比.
4.【解析】根据圆中最长的弦为直径求解.
解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
【点评】圆的弦长的取值范围0<L≤10.
5.【解析】由同弧所对的圆心角和圆周角的关系可得,∠AOB=2∠ACB,则结果即可得出.
解:由题意得,∠ACB=∠AOB=×80°=40°.
故选:D.
【点评】本题考查了圆心角、弧、弦的关系,重点是圆周角定理的应用.
6.【解析】由于直径是圆的最长弦,经过圆心的弦是直径,两点确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
解:圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选A.
【点评】本题考查了直径和弦的关系,直径是弦,弦不一定是直径,直径是圆内最长的弦.
二、填空题
7.【解析】利用半径相等可判断△OAB为等边三角形,然后根据等边三角形的性质易得AB=4cm.
解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等边三角形的判定与性质.
8.【解析】根据弦的定义进行分析,从而得到答案.
解:图中的弦有AE,DC,AD共三条,
故答案为:三,AE,DC,AD.
【点评】本题考查圆的认识,理解弦的定义是解决本题的关键.
9.【解析】设P的坐标是(x,y),根据勾股定理得出方程,求出方程的一组解即可.
解:设P的坐标是(x,y),
根据题意和勾股定理得出x2+y2=52,
x=3,y=4满足上式,
∵P在第二象限,
∴P(﹣3,4).
故答案为:(﹣3,4).
【点评】本题主要考查对点与圆的位置关系,坐标与图形性质,勾股定理等知识点的理解和掌握,能根据题意得出方程是解此题的关键.
10.【解析】直径是圆内最长的弦,则AB可能是直径,从而不难得到其取值范围.
解:圆的半径为3,则弦中最长的弦即直径的长度是6,因而弦AB长度的取值范围是0<AB≤6.
【点评】圆中的最长的弦是直径是解决本题的关键.
三、解答题
11.【解析】证明△BOE≌△COF,即可得到OE=OF,从而根据等式的性质得到CE=BF.
解:∵在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴OE=OF,
又∵OB=OC
∴CE=BF.
【点评】本题考查了圆的基本概念,以及全等三角形的判定与性质,正确证明两个三角形全等是关键.
12.【解析】根据在同圆或 ( http: / / www.21cnjy.com )等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等可得∠B=∠C,再根据三角形内角和定理可得答案.
解:在⊙O中,∵,
∴∠B=∠C,
∵∠A=40°,∠A+∠B+∠C=180°,
∴∠B==70°.
【点评】此题主要考查了圆心角、弧、弦的关系,关键是掌握在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
13.【解析】连接OD,利用三个角是直角的四边形是矩形判定四边形DEOF是矩形,利用矩形的对角线相等即可得到所求结论.
解:连接OD.
( http: / / www.21cnjy.com )
∵OC⊥AB DE⊥OC,DF⊥OA
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,
∴EF=OD.
∵OD=OA
∴EF=OA=4.
【点评】本题考查了圆的认识及矩形的判定与性质,解题的关键是利用矩形的判定方法判定四边形DFOE为矩形.
14.【解析】连结OC, ( http: / / www.21cnjy.com )如图,由CE=AO,OA=OC得到OC=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,
所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
解:连结OC,如图,
( http: / / www.21cnjy.com )
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
二、知识回顾 1.说出生活中与圆有关的物体. 车轮、碗底、柱子、方向盘、硬币等. 思考:车轮为什么做成圆形? 车轮设计成圆的,可以让车轮轴(圆心)到地面的距离不变,不至于颠簸. 2.小花、小强、小彬三人相邀掷飞镖比赛. ( http: / / www.21cnjy.com )他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜.如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好? ( http: / / www.21cnjy.com )
三、新知讲解 1.圆的有关概念①圆的定义有两种表达形式:如图,在平面内,线段OA绕它固定的一个端点O旋转一周,另一端点A所形成的图形叫做圆,记作“”,读作“圆O”.固定的端点O叫做 圆心 ,线段OA叫做 半径 . ( http: / / www.21cnjy.com )圆心为O,半径为r的圆可以看成是是平面内所有到定点O的距离等于定长r的点的集合.②连接圆上任意两点的线段叫做 弦 .③通过圆心的弦叫做 直径 .④圆上任意两点间的部分叫做圆弧,简称 弧 .⑤圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做 半圆 .⑥大于半圆的弧叫做 优弧 .⑦小于半圆的弧叫做 劣弧 .⑧能够重合的两个圆叫做等圆. 在同圆或等圆中,能够互相重合的弧叫做 等弧 .2.圆的内部、外部圆的内部可以看作是到圆心的距离 小于半径 的点的集合.圆的外部可以看作是到圆心的距离 大于半径 的点的集合.
四、典例探究 扫一扫,有惊喜哦!1.根据圆的基本概念判断说法正误【例1】(2015春 张掖校级月考)有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是( )A.1 B.2 C.3 D.4总结:与圆有关的概念我们要注意以下几点:1.确定圆的条件是圆心与半径.2.直径是弦,直径是圆内最长的弦.弦不一定是直径,只有过圆心的弦才是直径.3.半圆是弧,但弧不一定是半圆.练1.(2014秋 梁子湖区期末)车轮要做成圆形,实际上就是根据圆的特征( )A.圆上各点到圆心的距离相等 B.直径是圆中最长的弦C.同弧所对的圆周角相等 D.圆是中心对称图形2.求证正方形四个顶点共圆【例2】正方形ABCD的对角线AC,BD相交于点O.求证:A,B,C,D四个点在以O为圆心的同一个圆上. ( http: / / www.21cnjy.com )总结:证明四点共圆,关键是说明这四点到圆心的距离相等.常见的四点共圆的情况如下:矩形的四个顶点共圆;正方形的四个顶点共圆;有公共斜边的两个直角三角形的四个顶点共圆;对角互补的凸四边形的四个顶点共圆.练2.已知矩形的两边长分别为6和8,则矩形的四个顶点在以_____为圆心,以______为半径的圆上.3.利用同圆半径相等求解【例3】(2014秋 中山月考)如图,在R ( http: / / www.21cnjy.com )t△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A=_______. ( http: / / www.21cnjy.com )总结:根据同圆半径相等可得出等腰三角形,根据等腰三角形两底角相等,或结合三角形外角的性质、三角形内角和定理即可求得角的度数.练3.(2011秋 江宁区校级期中)如图,BD=OD,∠AOC=114°,求∠AOD的度数. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2014 长宁区一模)下列说法中,结论错误的是( )A.直径相等的两个圆是等圆B.长度相等的两条弧是等弧C.圆中最长的弦是直径D.一条弦把圆分成两条弧,这两条弧可能是等弧2.(2014秋 泰州校级期中)下列说法中,结论错误的是( )A.直径相等的两个圆是等圆B.三角形的外心是这个三角形三条角平分线的交点C.圆中最长的弦是直径D.一条弦把圆分成两条弧,这两条弧可能是等弧3.把圆的半径缩小到原来的,那么圆的面积缩小到原来的( )A. B. C. D.4.半径为5的圆的一条弦长不可能是( )A.3 B.5 C.10 D.125.(2015 茂名模拟)如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( ) ( http: / / www.21cnjy.com )A.80° B.70° C.60° D.40°6.(2010秋 张家港市校级月考)过圆上一点可以作出圆的最长弦的条数为( )A.1条 B.2条 C.3条 D.无数条二、填空题7.(2014秋 天河区校级期中)如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为______cm. ( http: / / www.21cnjy.com )8.(2014秋 丹阳市校级月考)如图,在 ( http: / / www.21cnjy.com )⊙O中,点A、O、D和点B、O、C分别在一条直线上,图中共有________条弦,它们分别是______________________. ( http: / / www.21cnjy.com )9.(2010秋 邗江区期 ( http: / / www.21cnjy.com )末)已知⊙O的半径为5,圆心在坐标原点,位于第二象限的该圆上的一点P的横坐标和纵坐标均为整数.则点P的坐标为________.(写出一个即可)10.圆的半径为3,则弦AB长度的取值范围是_______.三、解答题11.(2012春 翁源县校级月考)如 ( http: / / www.21cnjy.com )图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF. ( http: / / www.21cnjy.com )12.(2014 集美区一模)如图,在⊙O中,,∠A=40°,求∠B的度数. ( http: / / www.21cnjy.com )13.(2012秋 邗江区期中)如 ( http: / / www.21cnjy.com )图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长. ( http: / / www.21cnjy.com )14.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据弦的定义、弧的定义、以及确定圆的条件即可解决.
解:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的 ( http: / / www.21cnjy.com )任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
【点评】本题考查弦与直径的区别,弧与半圆的区别,及确定圆的条件,不要将弦与直径、弧与半圆混淆.
练1.【解析】根据车轮的特点和功能进行解答.
解:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选A.
【点评】本题考查了对圆的基本认识,即墨经所说:圆,一中同长也,属于基础知识,难度较小.
【例2】【解析】要说明几个点共圆的问题,只需证明这几个点到同一个点的距离相等,此题可以充分运用正方形的性质进行证明.
证明:∵四边形ABCD为正方形,
∴OA=OC=AC,OB=OD=BD,AC=BD.
∴OA=OB=OC=OD.
∴ A,B,C,D四个点在以O为圆心的同一个圆上.
【点评】此题考查了点和圆的位置关系,要掌握证明几点共圆的方法:即证明这些点到同一个点的距离相等.
练2.【解析】因矩形的对角线是圆的直径.所以两条对角线的交点为圆心,半径为5.
解:在矩形ABCD中,根据勾股定理求得:AC=BD==10,则OA=OC=OB=OD=5.
如图,
( http: / / www.21cnjy.com )
∵∠ABC=∠ADC=90°,
∴AC是直径,即矩形ABCD的四个顶点在以对角线交点为圆心,以5为半径的圆上.
故答案是:对角线交点;5.
【点评】本题考查了点与圆的位置关系.根据圆周角定理推知AC为直径是解题的关键.
【例3】【解析】由半径相等得CB=CD,则∠B=∠CDB,在根据三角形内角和计算出∠B=(180°﹣∠BCD)=70°,然后利用互余计算∠A的度数.
解:∵CB=CD,
∴∠B=∠CDB,
∵∠B+∠CDB+∠BCD=180°,
∴∠B=(180°﹣∠BCD)=(180°﹣40°)=70°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=20°.
故答案为20°.
【点评】本题考查了同圆半径相等.
练3.【解析】设∠B=x,根据等腰三角形的性 ( http: / / www.21cnjy.com )质,由BD=OD得∠DOB=∠B=x,再根据三角形外角性质得∠ADO=2x,则∠A=∠ADO=2x,然后根据三角形外角性质得2x+x=114°,解得x=38°,最后利用三角形内角和定理计算∠AOD的度数.
解:设∠B=x,
∵BD=OD,
∴∠DOB=∠B=x,
∴∠ADO=∠DOB+∠B=2x,
∵OA=OD,
∴∠A=∠ADO=2x,
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°,
∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
课后小测答案:
一、选择题
1.【解析】利用圆的有关定义进行判断后利用排除法即可得到正确的答案;
解:A、直径相等的两个圆是等圆,正确,不符合题意;
B、长度相等的两条弧圆周角不一定相等,它们不一定是等弧,原题的说法是错误的,符合题意;
C、圆中最长的弦是直径,正确,不符合题意;
D、一条直径把圆分成两条弧,这两条弧是等弧,正确,不符合题意,
故选:B.
【点评】本题考查了圆的认识,了解圆中有关的定义及性质是解答本题的关键.
2.【解析】根据等圆的定义对A进行判断;根据三角形外心的定义对B进行判断;根据直径的定义对C进行判断;根据等弧的定义对D进行判断.
解:A、直径相等的两个圆是等圆,所以A选项的说法正确;
B、三角形的外心是这个三角形三边的中垂线的交点,所以B选项的说法错误;
C、圆中最长的弦是直径,所以C选项的说法正确;
D、一条直径弦圆分成两条弧,这两条弧是等弧,所以D选项的说法正确.
故选:B.
【点评】本题考查了圆的认识:与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了矩形的性质.
3.【解析】因为圆的面积公式是:s=πr2,所以圆的面积和此圆半径的平方有关系,设出原圆的半径,再表示出现在圆的半径代入公式求解即可.
解:设原来的圆的半径为r,则面积s1=πr2,
∴缩小到原来的后,s2=π(r)2=πr2,
∴.
故选:D.
【点评】本题考查了圆的面积公式,在公式中:圆的面积和半径的平方成正比.
4.【解析】根据圆中最长的弦为直径求解.
解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
【点评】圆的弦长的取值范围0<L≤10.
5.【解析】由同弧所对的圆心角和圆周角的关系可得,∠AOB=2∠ACB,则结果即可得出.
解:由题意得,∠ACB=∠AOB=×80°=40°.
故选:D.
【点评】本题考查了圆心角、弧、弦的关系,重点是圆周角定理的应用.
6.【解析】由于直径是圆的最长弦,经过圆心的弦是直径,两点确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
解:圆的最长的弦是直径,直径经过圆心,过圆上一点和圆心可以确定一条直线,所以过圆上一点可以作出圆的最长弦的条数为一条.
故选A.
【点评】本题考查了直径和弦的关系,直径是弦,弦不一定是直径,直径是圆内最长的弦.
二、填空题
7.【解析】利用半径相等可判断△OAB为等边三角形,然后根据等边三角形的性质易得AB=4cm.
解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等边三角形的判定与性质.
8.【解析】根据弦的定义进行分析,从而得到答案.
解:图中的弦有AE,DC,AD共三条,
故答案为:三,AE,DC,AD.
【点评】本题考查圆的认识,理解弦的定义是解决本题的关键.
9.【解析】设P的坐标是(x,y),根据勾股定理得出方程,求出方程的一组解即可.
解:设P的坐标是(x,y),
根据题意和勾股定理得出x2+y2=52,
x=3,y=4满足上式,
∵P在第二象限,
∴P(﹣3,4).
故答案为:(﹣3,4).
【点评】本题主要考查对点与圆的位置关系,坐标与图形性质,勾股定理等知识点的理解和掌握,能根据题意得出方程是解此题的关键.
10.【解析】直径是圆内最长的弦,则AB可能是直径,从而不难得到其取值范围.
解:圆的半径为3,则弦中最长的弦即直径的长度是6,因而弦AB长度的取值范围是0<AB≤6.
【点评】圆中的最长的弦是直径是解决本题的关键.
三、解答题
11.【解析】证明△BOE≌△COF,即可得到OE=OF,从而根据等式的性质得到CE=BF.
解:∵在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴OE=OF,
又∵OB=OC
∴CE=BF.
【点评】本题考查了圆的基本概念,以及全等三角形的判定与性质,正确证明两个三角形全等是关键.
12.【解析】根据在同圆或 ( http: / / www.21cnjy.com )等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等可得∠B=∠C,再根据三角形内角和定理可得答案.
解:在⊙O中,∵,
∴∠B=∠C,
∵∠A=40°,∠A+∠B+∠C=180°,
∴∠B==70°.
【点评】此题主要考查了圆心角、弧、弦的关系,关键是掌握在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
13.【解析】连接OD,利用三个角是直角的四边形是矩形判定四边形DEOF是矩形,利用矩形的对角线相等即可得到所求结论.
解:连接OD.
( http: / / www.21cnjy.com )
∵OC⊥AB DE⊥OC,DF⊥OA
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,
∴EF=OD.
∵OD=OA
∴EF=OA=4.
【点评】本题考查了圆的认识及矩形的判定与性质,解题的关键是利用矩形的判定方法判定四边形DFOE为矩形.
14.【解析】连结OC, ( http: / / www.21cnjy.com )如图,由CE=AO,OA=OC得到OC=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,
所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
解:连结OC,如图,
( http: / / www.21cnjy.com )
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
同课章节目录
