【多媒体导学案】人教版数学九年级上册第24章第5课时圆周角(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第5课时圆周角(教师版) |  | |
| 格式 | zip | ||
| 文件大小 | 413.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 10:28:53 | ||
图片预览


文档简介
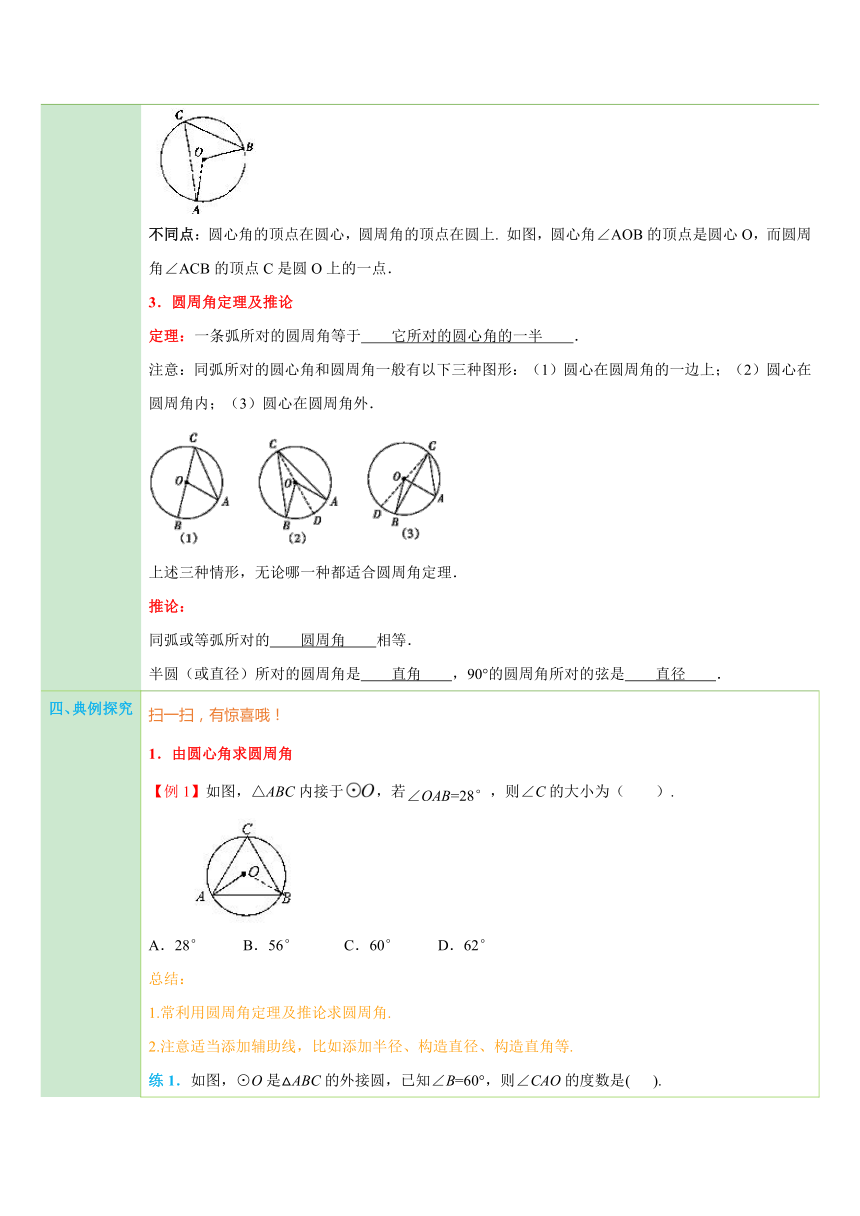
一、学习目标 1.了解圆周角的概念,理解圆周角定理及推理;2.熟练掌握圆周角定理及推理并灵活应用;3.体会分类思想.
二、知识回顾 1.什么是圆心角? 顶点在圆心的角叫做圆心角. 判断下列哪些角是圆心角:((1)) ( http: / / www.21cnjy.com )2.同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,那么它们所对应的其余各组量有什么关系? 相等 在同圆或等圆中,相等的圆心角所对的弧 相等 ,所对的弦 也相等 .在同圆或等圆中,相等的弧所对的 圆心角 相等,所对的 弦 也相等.在同圆或等圆中,相等的弦所对的 圆心角 相等, 所对的弧 相等.3.在圆心角、弧、弦之间的关系定理中,为什么要说“同圆或等圆中”?这个条件能不能去掉? 不能去掉.反例:如图,虽然圆心角,但,. ( http: / / www.21cnjy.com )
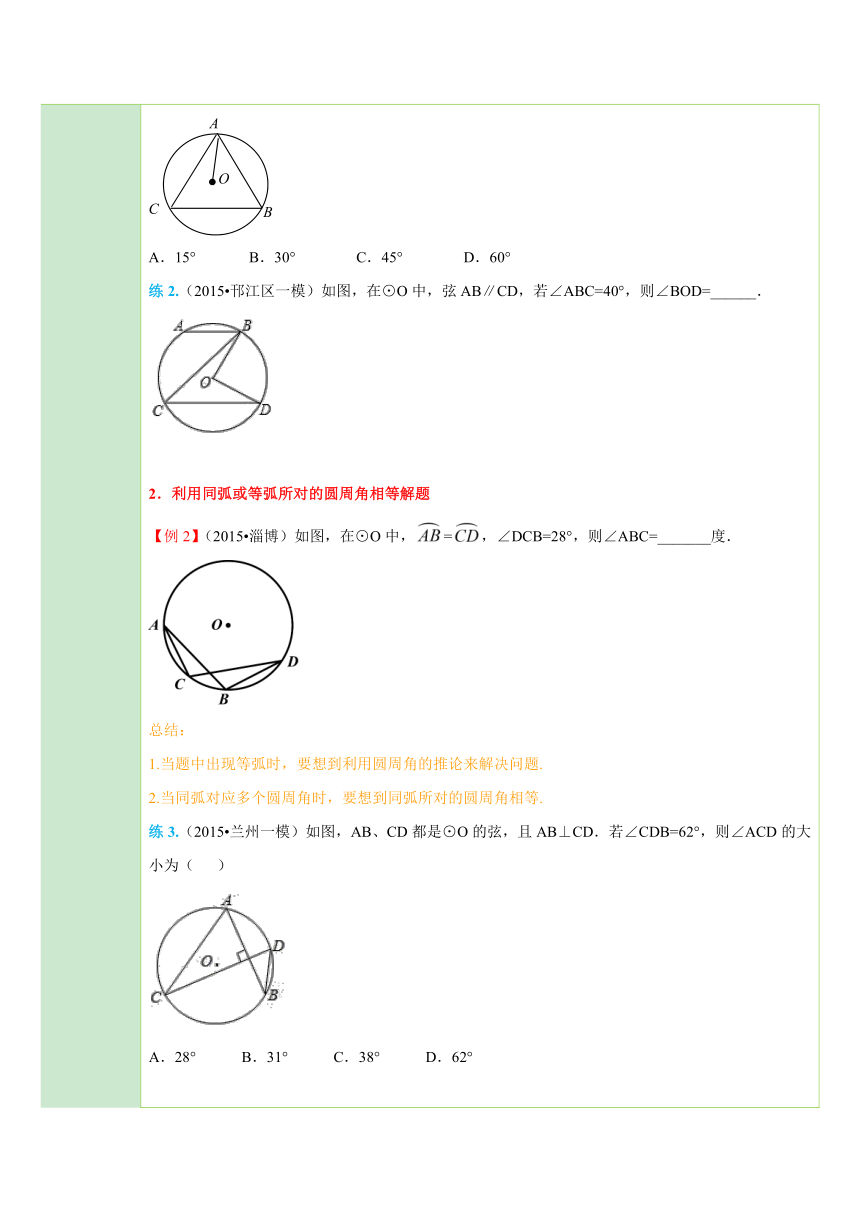
三、新知讲解 1.圆周角 顶点在圆上,并且两边都与圆相交的角 叫做圆周角.2.圆心角与圆周角的异同相同点:角的两边都与圆相交. 如图,圆心角∠AOB与圆周角∠ACB的两边都与圆O相交. ( http: / / www.21cnjy.com )不同点:圆心角的顶点在圆心,圆周角的顶点在圆上. 如图,圆心角∠AOB的顶点是圆心O,而圆周角∠ACB的顶点C是圆O上的一点.3.圆周角定理及推论定理:一条弧所对的圆周角等于 它所对的圆心角的一半 .注意:同弧所对的圆心角和圆周角一般有以下三种图形:(1)圆心在圆周角的一边上;(2)圆心在圆周角内;(3)圆心在圆周角外. ( http: / / www.21cnjy.com )上述三种情形,无论哪一种都适合圆周角定理.推论:同弧或等弧所对的 圆周角 相等.半圆(或直径)所对的圆周角是 直角 ,90°的圆周角所对的弦是 直径 .
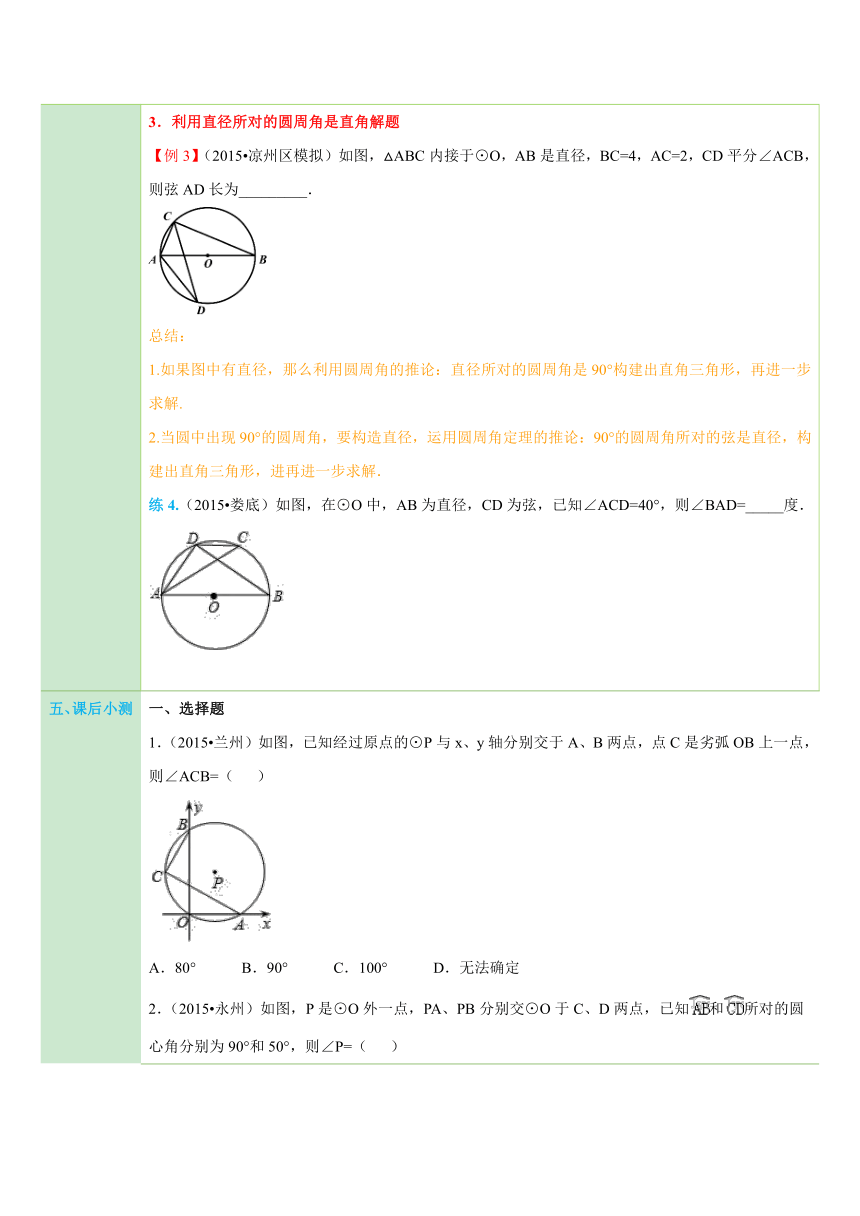
四、典例探究 扫一扫,有惊喜哦!1.由圆心角求圆周角【例1】如图,△ABC内接于,若∠OAB=28°,则∠C的大小为( ). ( http: / / www.21cnjy.com )A.28° B.56° C.60° D.62°总结:常利用圆周角定理及推论求圆周角.注意适当添加辅助线,比如添加半径、构造直径、构造直角等.练1.如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( ).A.15° B.30° C.45° D.60°练2.(2015 邗江区一模)如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=______. ( http: / / www.21cnjy.com )2.利用同弧或等弧所对的圆周角相等解题【例2】(2015 淄博)如图,在⊙O中,=,∠DCB=28°,则∠ABC=_______度. ( http: / / www.21cnjy.com )总结:当题中出现等弧时,要想到利用圆周角的推论来解决问题.当同弧对应多个圆周角时,要想到同弧所对的圆周角相等.练3.(2015 兰州一模)如图,AB、CD都是⊙O的弦,且AB⊥CD.若∠CDB=62°,则∠ACD的大小为( ) ( http: / / www.21cnjy.com )A.28° B.31° C.38° D.62°3.利用直径所对的圆周角是直角解题【例3】(2015 凉州区模拟)如图,△ ( http: / / www.21cnjy.com )ABC内接于⊙O,AB是直径,BC=4,AC=2,CD平分∠ACB,则弦AD长为_________. ( http: / / www.21cnjy.com )总结:如果图中有直径,那么利用圆周角的推论:直径所对的圆周角是90°构建出直角三角形,再进一步求解.当圆中出现90°的圆周角,要构造直径,运用圆周角定理的推论:90°的圆周角所对的弦是直径,构建出直角三角形,进再进一步求解.练4.(2015 娄底)如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=_____度. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2015 兰州)如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=( ) ( http: / / www.21cnjy.com )A.80° B.90° C.100° D.无法确定2.(2015 永州)如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知和所对的圆心角分别为90°和50°,则∠P=( ) ( http: / / www.21cnjy.com )A.45° B.40° C.25° D.20°3.(2015 河池)如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( ) ( http: / / www.21cnjy.com )A.60° B.48° C.30° D.24°4.(2015 江宁区一模)如图⊙P经过点A(0,)、O(0,0)、B(1,0),点C在第一象限的上,则∠BCO的度数为( ) ( http: / / www.21cnjy.com )A.15° B.30° C.45° D.60°5.(2015 酒泉)△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )A.80° B.160° C.100° D.80°或100°6.(2015 威海)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( ) ( http: / / www.21cnjy.com )A.68° B.88° C.90° D.112°二、填空题7.(2015 黄冈中学自主招生)已知,如 ( http: / / www.21cnjy.com )图,AB是⊙O的直径,点D,C在⊙O上,连接AD、BD、DC、AC,如果∠BAD=25°,那么∠C的度数是______. ( http: / / www.21cnjy.com )8.(2015 番禺区一模)如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD=_____. ( http: / / www.21cnjy.com )9.(2015 滨湖区二模)将量角器按如图 ( http: / / www.21cnjy.com )所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为_______. ( http: / / www.21cnjy.com )三、解答题10.(2015 平顶山三模)已知,如图,AB⊥CD,BE是⊙O的直径,(1)求证:AE∥CD;(2)若AC=3,求出DE的长. ( http: / / www.21cnjy.com )11.如图,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D、E,且=.求证:△ABC是等腰三角形. ( http: / / www.21cnjy.com )12.(2015 安徽)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值. ( http: / / www.21cnjy.com )13.(2015 温州模拟 ( http: / / www.21cnjy.com ))如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.(1)求BE的长;(2)求△ACD外接圆的半径. ( http: / / www.21cnjy.com )14.(2014秋 天门期末)如图,AB是⊙O的直径,C,P是上两点,AB=10,AC=6.(1)如图1,若点P是的中点,求PA的长;(2)如图2,若点P是的中点,求PA的长. ( http: / / www.21cnjy.com )15.(2015 东西湖区校级模拟)(1)如图1,PA、PB是⊙O的两条弦,AB为直径,C为的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明(2)如图2,PA、PB是⊙O的两条弦,AB为弦,C为劣弧的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明 ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】本题考查了圆周角和圆心角之间的关系,欲求的大小,需先求出所对弧对的圆心角的度数.
解:连接OB,则OA=OB. ∴∠OAB=∠OBA.
∵∠OAB=28°, ∴∠AOB=124°.
∴=62°.
故选D.
【点评】运用同弧所对圆周角与圆心角的关系时,常常构造出同弧所对的圆心角.
练1.【解析】要求∠CAO的度数,可连接CO,运用“同弧所对的圆周角等于圆心角的一半”和同圆半径相等求解.
解:连接CO,则∠AOC=∠B=120°.
∵AO=CO,∴∴∠CAO=∠ACO=30°.
故选B.
【点评】连接半径是圆中常见的辅助线作法.
练2.【解析】根据平行线的性质由AB∥CD得到∠C=∠ABC=40°,然后根据圆周角定理求解.
解:∵AB∥CD,
∴∠C=∠ABC=40°,
∴∠BOD=2∠C=80°.
故答案为80°.
【点评】本题考查了圆周角定理:在同圆或 ( http: / / www.21cnjy.com )等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了平行线的性质.
【例2】【解析】首先根据=,可得;然后根据同弧或等弧所对的圆周角相等,由∠DCB=28°,可得∠ABC=28°,据此解答即可.
解:∵=,
∴;
又∵∠DCB=28°,
∴∠ABC=28°.
故答案为:28.
【点评】此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:同弧或等弧所对的圆周角相等.
练2.【解析】利用垂直的定义得到∠ ( http: / / www.21cnjy.com )DPB=90°,再根据三角形内角和定理求出∠B=180°﹣90°﹣62°=28°,然后根据圆周角定理即可得到∠ACD的度数.
解:∵AB⊥CD,
( http: / / www.21cnjy.com )
∴∠DPB=90°,
∵∠CDB=62°,
∴∠B=180°﹣90°﹣62°=28°,
∴∠ACD=∠B=28°.
故选A.
【点评】本题考查了圆周角定理:同弧或等弧所对的圆周角相等.
【例3】【解析】连接BD,首先证明∠1=∠2,得到AD=BD,然后再根据勾股定理可得AD长.
解:连接BD,
( http: / / www.21cnjy.com )
∵AB为直径,CD平分∠ACB交⊙O于D,
∴∠ACD=∠BCD=45°,
∵∠1=∠ACD,∠2=∠DCB,
∴∠1=∠2,
∴AD=BD,
∵BC=4,AC=2,
∴AB2=42+22=20,
∴AD2+DB2=20,
∴AD=.
故答案为:.
【点评】此题主要考查了圆周角定理及其推论,关键是掌握圆周角定理:同弧或等弧所对的圆周角相等,直径所对的圆周角等于90°.
练4.【解析】由在⊙O中,AB为直 ( http: / / www.21cnjy.com )径,根据直径所对的圆周角是直角,可求得∠ADB=90°,又由圆周角定理,可求得∠B=∠ACD=40°,继而求得答案.
解:∵在⊙O中,AB为直径,
∴∠ADB=90°,
∵∠B=∠ACD=40°,
∴∠BAD=90°﹣∠B=50°.
故答案为:50.
【点评】此题考查了圆周角定理.注意在同圆或等 ( http: / / www.21cnjy.com )圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角.
课后小测答案:
一、选择题
1.【解析】由∠AOB与∠ACB是优弧AB所对的圆周角,根据圆周角定理,即可求得∠ACB=∠AOB=90°.
解:∵∠AOB与∠ACB是优弧AB所对的圆周角,
∴∠AOB=∠ACB,
∵∠AOB=90°,
∴∠ACB=90°.
故选:B.
【点评】此题考查了圆周角定理.此题比较简单,解题的关键是观察图形,得到∠AOB与∠ACB是优弧AB所对的圆周角.
2.【解析】先由圆周角定理求出∠A与∠ADB的度数,然后根据三角形外角的性质即可求出∠P的度数.
解:∵和所对的圆心角分别为90°和50°,
∴∠A=25°,∠ADB=45°,
∵∠P+∠A=∠ADB,
∴∠P=∠ADB﹣∠P=45°﹣25°=20°.
故选:D.
【点评】此题考查了圆周角定理及三角形外角的性质,解题的关键是:熟记并能灵活应用圆周角定理及三角形外角的性质解题.
3.【解析】先根据垂径定理得到=,然后根据圆周角定理求解.
解:∵直径AB⊥CD,
∴=,
∴∠BAC=∠BOD=×48°=24°.
故选:D.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.
4.【解析】连接AB,求出∠OAB的度数,由圆周角定理可得出∠BCO的度数.
解:连接AB,
( http: / / www.21cnjy.com )
∵A(0,),B(1,0),
∴OA=,OB=1.
在Rt△AOB中,AB=2,
∴∠OAB=30°,
∴∠OCB=∠OAB=30°(圆周角定理).
故选:B.
【点评】本题考查了圆周角定理,注意熟练掌握:同弧或等弧所对的圆周角相等.
5.【解析】首先根据题意画出图形,由圆周角定理即可求得答案∠ABC的度数,又由圆的内接四边形的性质,即可求得∠ABC的度数.
解:如图,
( http: / / www.21cnjy.com )
∵∠AOC=160°,
∴∠ABC=∠AOC=×160°=80°,
∵∠ABC+∠AB′C=180°,
∴∠AB′C=180°﹣∠ABC=180°﹣80°=100°.
∴∠ABC的度数是:80°或100°.
故选:D.
【点评】此题考查了圆周角定理与圆的内接四边形的性质.此题难度不大,注意数形结合思想与分类讨论思想的应用,注意别漏解.
6.【解析】如图,作辅助圆 ( http: / / www.21cnjy.com );首先运用圆周角定理证明∠CAD=2∠CBD,∠BAC=2∠BDC,结合已知条件∠CBD=2∠BDC,得到∠CAD=2∠BAC,即可解决问题.
解:如图,
( http: / / www.21cnjy.com )
∵AB=AC=AD,
∴点B、C、D在以点A为圆心,
以AB的长为半径的圆上;
∵∠CBD=2∠BDC,
∠CAD=2∠CBD,∠BAC=2∠BDC,
∴∠CAD=2∠BAC,而∠BAC=44°,
∴∠CAD=88°,
故选:B.
【点评】该题主要考查了圆 ( http: / / www.21cnjy.com )周角定理及其推论等几何知识点及其应用问题;解题的方法是作辅助圆,将分散的条件集中;解题的关键是灵活运用圆周角定理及其推论等几何知识点来分析、判断、推理或解答.
二、填空题
7.【解析】因为AB是⊙O的直径,所以求得∠ADB=90°,进而求得∠B的度数,又因为∠B=∠C,所以∠C的度数可求出.
解:∵AB是⊙0的直径,
∴∠ADB=90°.
∵∠BAD=25°,
∴∠B=65°,
∴∠C=∠B=65°(同弧所对的圆周角相等).
故答案为:65°.
【点评】本题考查圆周角定理中的两个推论:①直径所对的圆周角是直角②同弧所对的圆周角相等.
8.【解析】根据圆周角定理求得∠AOD ( http: / / www.21cnjy.com )=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半)、∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);根据平角是180°知∠BOD=180°﹣∠AOD,故∠BCD=32°.
解:连接OD.
( http: / / www.21cnjy.com )
∵AB是⊙0的直径,CD是⊙O的弦,∠ABD=58°,
∴∠AOD=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半);
又∵∠BOD=180°﹣∠AOD,∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);
∴∠BCD=32°;
另法:∵AB为直径,
∴∠ADB=90°,
∵∠ABD=58°,
∴∠A=90°﹣58°=32°,
∵∠BCD和∠A都是BD所对圆周角,
∴∠BCD=32°.
故答案为:32°.
【点评】本题考查了圆周角定理.解答此题 ( http: / / www.21cnjy.com )时,通过作辅助线OD,将隐含在题中的圆周角与圆心角的关系(同弧所对的圆周角是所对的圆心角的一半)显现出来.
9.【解析】连接CE.可得∠ECB=90°,∠ACB=110°,再根据等腰三角形的性质和三角形内角和定理即可求解.
解:连接CE.
( http: / / www.21cnjy.com )
可得∠ECB=160°﹣70°=90°,∠ACB=160°﹣50°=110°,
∴∠B=(180°﹣90°)÷2=45°,
∴∠A=180°﹣∠ACB﹣∠B=25°.
故答案为25°.
【点评】本题考查了等腰三角形的性质和三角形内角和定理,得到∠B和∠ACB的度数是解题的关键.
三、解答题
10.【解析】(1)直接利用圆周角定理结合垂直于同一直线的两条直线互相平行得出即可;
(2)利用平行弦之间所夹的弧相等进而得出答案.
(1)证明:∵BE是⊙O的直径,
∴∠BAE=90°,即AE⊥AB
又∵AB⊥CD,
∴AE∥CD;
(2)解:∵AE∥CD,
∴=,
∴AC=DE=3.
【点评】此题主要考查了圆周角定理以及平行弦之间的关系,正确应用圆周角定理是解题关键.
11.【解析】连结AE,如图,根据圆周角定理,由=得∠DAE=∠BAE,由AB为直径得∠AEB=90°,根据等腰三角形的判定方法即可得△ABC为等腰三角形;
证明:连结AE,如图,
( http: / / www.21cnjy.com )
∵=,∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∴△ABC为等腰三角形.
【点评】本题考查了圆周角定理:在同 ( http: / / www.21cnjy.com )圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质和勾股定理.
12.【解析】(1)连结OQ,如图1,由PQ∥AB,OP⊥PQ得到OP⊥AB,在Rt△OBP中,利用正切定义可计算出OP=3tan30°=,然后在Rt△OPQ中利用勾股定理可计算出PQ=;
(2)连结OQ,如图2,在Rt△OPQ中,根据勾股定理得到PQ=,则当OP的长最小时,PQ的长最大,根据垂线段最短得到OP⊥BC,则OP=OB=,所以PQ长的最大值=.
解:(1)连结OQ,如图1,
( http: / / www.21cnjy.com )
∵PQ∥AB,OP⊥PQ,
∴OP⊥AB,
在Rt△OBP中,∵tan∠B=,
∴OP=3tan30°=,
在Rt△OPQ中,∵OP=,OQ=3,
∴PQ==;
(2)连结OQ,如图2,
( http: / / www.21cnjy.com )
在Rt△OPQ中,PQ==,
当OP的长最小时,PQ的长最大,
此时OP⊥BC,则OP=OB=,
∴PQ长的最大值为=.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了勾股定理和解直角三角形.
13.【解析】(1)由圆O的圆周角∠AC ( http: / / www.21cnjy.com )B=90°,根据90°的圆周角所对的弦为圆的直径得到AD为圆O的直径,再根据直径所对的圆周角为直角可得三角形ADE为直角三角形,又AD是△ABC的角平分线,可得一对角相等,而这对角都为圆O的圆周角,根据同圆或等圆中,相等的圆周角所对的弦相等可得CD=ED,利用HL可证明直角三角形ACD与AED全等,根据全等三角形的对应边相等即可得得出AC=AE,进而得出BE的长;
(2)由第一问的结论AE=AC,用A ( http: / / www.21cnjy.com )B﹣AE可求出EB的长,再由(1)∠AED=90°,得到DE与AB垂直,可得三角形BDE为直角三角形,设DE=CD=x,用CB﹣CD表示出BD=12﹣x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为CD的长,在直角三角形ACD中,由AC及CD的长,利用勾股定理即可求出AD的长,进而得出外接圆半径.
解:(1)∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),
∴∠AED=90°(直径所对的圆周角为直角),
又AD是△ABC的角平分线(已知),
∴∠CAD=∠EAD(角平分线定义),
∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE(全等三角形的对应边相等);
∵△ABC为直角三角形,且AC=5,CB=12,
∴根据勾股定理得:AB==13,
∴BE=13﹣AC=13﹣5=8;
(2)由(1)得到∠AED=90°,则有∠BED=90°,
设CD=DE=x,则DB=BC﹣CD=12﹣x,EB=AB﹣AE=AB﹣AC=13﹣5=8,
在Rt△BED中,根据勾股定理得:BD2=BE2+ED2,
即(12﹣x)2=x2+82,
解得:x=,
∴CD=,又AC=5,△ACD为直角三角形,
∴根据勾股定理得:AD==,
根据AD是△ACD外接圆直径,
∴△ACD外接圆的半径为:×=.
【点评】此题考查了圆周角定理,勾股定理 ( http: / / www.21cnjy.com ),以及全等三角形的判定与性质,利用了转化的思想,本题的思路为:根据圆周角定理得出直角,利用勾股定理构造方程来求解,从而得到解决问题的目的,灵活运用圆周角定理及勾股定理是解本题的关键.
14.【解析】(1)连结PB,如图1,根据圆周角定理得到∠APB=90°,根据圆心角、弧、弦的关系由=得到PA=PB,则△PAB为等腰直角三角形,所以PA=AB=;
(2)连结BC、BP、PO,OP交BC于H,根据圆周角定理得,∠APB=∠ACB=90°,再根据垂径定理得OP⊥BC,则OH=AC=3,在Rt△OBH中利用勾股定理计算出BH=4,在Rt△PBH中计算出PB=2,然后在Rt△ABP中利用勾股定理可计算出PB=4.
解:(1)连结PB,如图1,
( http: / / www.21cnjy.com )
∵AB是⊙O的直径,
∴∠APB=90°,
∵点P是的中点,
∴=,
∴PA=PB,
∴△PAB为等腰直角三角形,
∴PA=AB=×10=5;
(2)连结BC、BP、PO,OP交BC于H,如图2,
( http: / / www.21cnjy.com )
∵AB是⊙O的直径,
∴∠APB=∠ACB=90°,
∵点P是的中点,
∴OP⊥BC,
∴BH=CH,
∴OH=AC=3,
在Rt△OBH中,∵OB=5,OH=3,
∴BH==4,
在Rt△PBH中,∵PH=OP﹣OH=5﹣3=2,BH=4,
∴PB==2,
在Rt△ABP中,∵AB=10,PB=2,
∴PA==4.
【点评】本题考查了圆周角定理及其推论,也考查了勾股定理.
15.【解析】(1)根据圆周角定理和勾股定理得到AB=AC;
(2)在AE上截取AF=BP,连结AC、BC、FC、PC,如图2,由=得到AC=BC,再证明△CAF≌△CBP,得到CF=CP,由于弦CD⊥PA于E,根据等腰三角形的性质得EF=EP,于是有AE=PB+PE.
解:(1)AB=AC.理由如下:
∵AB为直径,C为的中点,
∴△ABC是等腰直角三角形,
∴AB=AC;
(2)AE=PB+PE.理由如下:
在AE上截取AF=BP,连结AC、BC、FC、PC,如图,
( http: / / www.21cnjy.com )
∵C为劣弧的中点,即=,
∴AC=BC,
在△CAF和△CBP中
,
∴△CAF≌△CBP,
∴CF=CP,
∵弦CD⊥PA于E,
∴EF=EP,
∴AE=AF+EF=PB+PE.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了全等三角形的判定与性质.
A
C
B
O
二、知识回顾 1.什么是圆心角? 顶点在圆心的角叫做圆心角. 判断下列哪些角是圆心角:((1)) ( http: / / www.21cnjy.com )2.同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,那么它们所对应的其余各组量有什么关系? 相等 在同圆或等圆中,相等的圆心角所对的弧 相等 ,所对的弦 也相等 .在同圆或等圆中,相等的弧所对的 圆心角 相等,所对的 弦 也相等.在同圆或等圆中,相等的弦所对的 圆心角 相等, 所对的弧 相等.3.在圆心角、弧、弦之间的关系定理中,为什么要说“同圆或等圆中”?这个条件能不能去掉? 不能去掉.反例:如图,虽然圆心角,但,. ( http: / / www.21cnjy.com )
三、新知讲解 1.圆周角 顶点在圆上,并且两边都与圆相交的角 叫做圆周角.2.圆心角与圆周角的异同相同点:角的两边都与圆相交. 如图,圆心角∠AOB与圆周角∠ACB的两边都与圆O相交. ( http: / / www.21cnjy.com )不同点:圆心角的顶点在圆心,圆周角的顶点在圆上. 如图,圆心角∠AOB的顶点是圆心O,而圆周角∠ACB的顶点C是圆O上的一点.3.圆周角定理及推论定理:一条弧所对的圆周角等于 它所对的圆心角的一半 .注意:同弧所对的圆心角和圆周角一般有以下三种图形:(1)圆心在圆周角的一边上;(2)圆心在圆周角内;(3)圆心在圆周角外. ( http: / / www.21cnjy.com )上述三种情形,无论哪一种都适合圆周角定理.推论:同弧或等弧所对的 圆周角 相等.半圆(或直径)所对的圆周角是 直角 ,90°的圆周角所对的弦是 直径 .
四、典例探究 扫一扫,有惊喜哦!1.由圆心角求圆周角【例1】如图,△ABC内接于,若∠OAB=28°,则∠C的大小为( ). ( http: / / www.21cnjy.com )A.28° B.56° C.60° D.62°总结:常利用圆周角定理及推论求圆周角.注意适当添加辅助线,比如添加半径、构造直径、构造直角等.练1.如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( ).A.15° B.30° C.45° D.60°练2.(2015 邗江区一模)如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=______. ( http: / / www.21cnjy.com )2.利用同弧或等弧所对的圆周角相等解题【例2】(2015 淄博)如图,在⊙O中,=,∠DCB=28°,则∠ABC=_______度. ( http: / / www.21cnjy.com )总结:当题中出现等弧时,要想到利用圆周角的推论来解决问题.当同弧对应多个圆周角时,要想到同弧所对的圆周角相等.练3.(2015 兰州一模)如图,AB、CD都是⊙O的弦,且AB⊥CD.若∠CDB=62°,则∠ACD的大小为( ) ( http: / / www.21cnjy.com )A.28° B.31° C.38° D.62°3.利用直径所对的圆周角是直角解题【例3】(2015 凉州区模拟)如图,△ ( http: / / www.21cnjy.com )ABC内接于⊙O,AB是直径,BC=4,AC=2,CD平分∠ACB,则弦AD长为_________. ( http: / / www.21cnjy.com )总结:如果图中有直径,那么利用圆周角的推论:直径所对的圆周角是90°构建出直角三角形,再进一步求解.当圆中出现90°的圆周角,要构造直径,运用圆周角定理的推论:90°的圆周角所对的弦是直径,构建出直角三角形,进再进一步求解.练4.(2015 娄底)如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=_____度. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2015 兰州)如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=( ) ( http: / / www.21cnjy.com )A.80° B.90° C.100° D.无法确定2.(2015 永州)如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知和所对的圆心角分别为90°和50°,则∠P=( ) ( http: / / www.21cnjy.com )A.45° B.40° C.25° D.20°3.(2015 河池)如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( ) ( http: / / www.21cnjy.com )A.60° B.48° C.30° D.24°4.(2015 江宁区一模)如图⊙P经过点A(0,)、O(0,0)、B(1,0),点C在第一象限的上,则∠BCO的度数为( ) ( http: / / www.21cnjy.com )A.15° B.30° C.45° D.60°5.(2015 酒泉)△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是( )A.80° B.160° C.100° D.80°或100°6.(2015 威海)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( ) ( http: / / www.21cnjy.com )A.68° B.88° C.90° D.112°二、填空题7.(2015 黄冈中学自主招生)已知,如 ( http: / / www.21cnjy.com )图,AB是⊙O的直径,点D,C在⊙O上,连接AD、BD、DC、AC,如果∠BAD=25°,那么∠C的度数是______. ( http: / / www.21cnjy.com )8.(2015 番禺区一模)如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD=_____. ( http: / / www.21cnjy.com )9.(2015 滨湖区二模)将量角器按如图 ( http: / / www.21cnjy.com )所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为_______. ( http: / / www.21cnjy.com )三、解答题10.(2015 平顶山三模)已知,如图,AB⊥CD,BE是⊙O的直径,(1)求证:AE∥CD;(2)若AC=3,求出DE的长. ( http: / / www.21cnjy.com )11.如图,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D、E,且=.求证:△ABC是等腰三角形. ( http: / / www.21cnjy.com )12.(2015 安徽)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值. ( http: / / www.21cnjy.com )13.(2015 温州模拟 ( http: / / www.21cnjy.com ))如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.(1)求BE的长;(2)求△ACD外接圆的半径. ( http: / / www.21cnjy.com )14.(2014秋 天门期末)如图,AB是⊙O的直径,C,P是上两点,AB=10,AC=6.(1)如图1,若点P是的中点,求PA的长;(2)如图2,若点P是的中点,求PA的长. ( http: / / www.21cnjy.com )15.(2015 东西湖区校级模拟)(1)如图1,PA、PB是⊙O的两条弦,AB为直径,C为的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明(2)如图2,PA、PB是⊙O的两条弦,AB为弦,C为劣弧的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明 ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】本题考查了圆周角和圆心角之间的关系,欲求的大小,需先求出所对弧对的圆心角的度数.
解:连接OB,则OA=OB. ∴∠OAB=∠OBA.
∵∠OAB=28°, ∴∠AOB=124°.
∴=62°.
故选D.
【点评】运用同弧所对圆周角与圆心角的关系时,常常构造出同弧所对的圆心角.
练1.【解析】要求∠CAO的度数,可连接CO,运用“同弧所对的圆周角等于圆心角的一半”和同圆半径相等求解.
解:连接CO,则∠AOC=∠B=120°.
∵AO=CO,∴∴∠CAO=∠ACO=30°.
故选B.
【点评】连接半径是圆中常见的辅助线作法.
练2.【解析】根据平行线的性质由AB∥CD得到∠C=∠ABC=40°,然后根据圆周角定理求解.
解:∵AB∥CD,
∴∠C=∠ABC=40°,
∴∠BOD=2∠C=80°.
故答案为80°.
【点评】本题考查了圆周角定理:在同圆或 ( http: / / www.21cnjy.com )等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半.也考查了平行线的性质.
【例2】【解析】首先根据=,可得;然后根据同弧或等弧所对的圆周角相等,由∠DCB=28°,可得∠ABC=28°,据此解答即可.
解:∵=,
∴;
又∵∠DCB=28°,
∴∠ABC=28°.
故答案为:28.
【点评】此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:同弧或等弧所对的圆周角相等.
练2.【解析】利用垂直的定义得到∠ ( http: / / www.21cnjy.com )DPB=90°,再根据三角形内角和定理求出∠B=180°﹣90°﹣62°=28°,然后根据圆周角定理即可得到∠ACD的度数.
解:∵AB⊥CD,
( http: / / www.21cnjy.com )
∴∠DPB=90°,
∵∠CDB=62°,
∴∠B=180°﹣90°﹣62°=28°,
∴∠ACD=∠B=28°.
故选A.
【点评】本题考查了圆周角定理:同弧或等弧所对的圆周角相等.
【例3】【解析】连接BD,首先证明∠1=∠2,得到AD=BD,然后再根据勾股定理可得AD长.
解:连接BD,
( http: / / www.21cnjy.com )
∵AB为直径,CD平分∠ACB交⊙O于D,
∴∠ACD=∠BCD=45°,
∵∠1=∠ACD,∠2=∠DCB,
∴∠1=∠2,
∴AD=BD,
∵BC=4,AC=2,
∴AB2=42+22=20,
∴AD2+DB2=20,
∴AD=.
故答案为:.
【点评】此题主要考查了圆周角定理及其推论,关键是掌握圆周角定理:同弧或等弧所对的圆周角相等,直径所对的圆周角等于90°.
练4.【解析】由在⊙O中,AB为直 ( http: / / www.21cnjy.com )径,根据直径所对的圆周角是直角,可求得∠ADB=90°,又由圆周角定理,可求得∠B=∠ACD=40°,继而求得答案.
解:∵在⊙O中,AB为直径,
∴∠ADB=90°,
∵∠B=∠ACD=40°,
∴∠BAD=90°﹣∠B=50°.
故答案为:50.
【点评】此题考查了圆周角定理.注意在同圆或等 ( http: / / www.21cnjy.com )圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角.
课后小测答案:
一、选择题
1.【解析】由∠AOB与∠ACB是优弧AB所对的圆周角,根据圆周角定理,即可求得∠ACB=∠AOB=90°.
解:∵∠AOB与∠ACB是优弧AB所对的圆周角,
∴∠AOB=∠ACB,
∵∠AOB=90°,
∴∠ACB=90°.
故选:B.
【点评】此题考查了圆周角定理.此题比较简单,解题的关键是观察图形,得到∠AOB与∠ACB是优弧AB所对的圆周角.
2.【解析】先由圆周角定理求出∠A与∠ADB的度数,然后根据三角形外角的性质即可求出∠P的度数.
解:∵和所对的圆心角分别为90°和50°,
∴∠A=25°,∠ADB=45°,
∵∠P+∠A=∠ADB,
∴∠P=∠ADB﹣∠P=45°﹣25°=20°.
故选:D.
【点评】此题考查了圆周角定理及三角形外角的性质,解题的关键是:熟记并能灵活应用圆周角定理及三角形外角的性质解题.
3.【解析】先根据垂径定理得到=,然后根据圆周角定理求解.
解:∵直径AB⊥CD,
∴=,
∴∠BAC=∠BOD=×48°=24°.
故选:D.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.
4.【解析】连接AB,求出∠OAB的度数,由圆周角定理可得出∠BCO的度数.
解:连接AB,
( http: / / www.21cnjy.com )
∵A(0,),B(1,0),
∴OA=,OB=1.
在Rt△AOB中,AB=2,
∴∠OAB=30°,
∴∠OCB=∠OAB=30°(圆周角定理).
故选:B.
【点评】本题考查了圆周角定理,注意熟练掌握:同弧或等弧所对的圆周角相等.
5.【解析】首先根据题意画出图形,由圆周角定理即可求得答案∠ABC的度数,又由圆的内接四边形的性质,即可求得∠ABC的度数.
解:如图,
( http: / / www.21cnjy.com )
∵∠AOC=160°,
∴∠ABC=∠AOC=×160°=80°,
∵∠ABC+∠AB′C=180°,
∴∠AB′C=180°﹣∠ABC=180°﹣80°=100°.
∴∠ABC的度数是:80°或100°.
故选:D.
【点评】此题考查了圆周角定理与圆的内接四边形的性质.此题难度不大,注意数形结合思想与分类讨论思想的应用,注意别漏解.
6.【解析】如图,作辅助圆 ( http: / / www.21cnjy.com );首先运用圆周角定理证明∠CAD=2∠CBD,∠BAC=2∠BDC,结合已知条件∠CBD=2∠BDC,得到∠CAD=2∠BAC,即可解决问题.
解:如图,
( http: / / www.21cnjy.com )
∵AB=AC=AD,
∴点B、C、D在以点A为圆心,
以AB的长为半径的圆上;
∵∠CBD=2∠BDC,
∠CAD=2∠CBD,∠BAC=2∠BDC,
∴∠CAD=2∠BAC,而∠BAC=44°,
∴∠CAD=88°,
故选:B.
【点评】该题主要考查了圆 ( http: / / www.21cnjy.com )周角定理及其推论等几何知识点及其应用问题;解题的方法是作辅助圆,将分散的条件集中;解题的关键是灵活运用圆周角定理及其推论等几何知识点来分析、判断、推理或解答.
二、填空题
7.【解析】因为AB是⊙O的直径,所以求得∠ADB=90°,进而求得∠B的度数,又因为∠B=∠C,所以∠C的度数可求出.
解:∵AB是⊙0的直径,
∴∠ADB=90°.
∵∠BAD=25°,
∴∠B=65°,
∴∠C=∠B=65°(同弧所对的圆周角相等).
故答案为:65°.
【点评】本题考查圆周角定理中的两个推论:①直径所对的圆周角是直角②同弧所对的圆周角相等.
8.【解析】根据圆周角定理求得∠AOD ( http: / / www.21cnjy.com )=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半)、∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);根据平角是180°知∠BOD=180°﹣∠AOD,故∠BCD=32°.
解:连接OD.
( http: / / www.21cnjy.com )
∵AB是⊙0的直径,CD是⊙O的弦,∠ABD=58°,
∴∠AOD=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半);
又∵∠BOD=180°﹣∠AOD,∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);
∴∠BCD=32°;
另法:∵AB为直径,
∴∠ADB=90°,
∵∠ABD=58°,
∴∠A=90°﹣58°=32°,
∵∠BCD和∠A都是BD所对圆周角,
∴∠BCD=32°.
故答案为:32°.
【点评】本题考查了圆周角定理.解答此题 ( http: / / www.21cnjy.com )时,通过作辅助线OD,将隐含在题中的圆周角与圆心角的关系(同弧所对的圆周角是所对的圆心角的一半)显现出来.
9.【解析】连接CE.可得∠ECB=90°,∠ACB=110°,再根据等腰三角形的性质和三角形内角和定理即可求解.
解:连接CE.
( http: / / www.21cnjy.com )
可得∠ECB=160°﹣70°=90°,∠ACB=160°﹣50°=110°,
∴∠B=(180°﹣90°)÷2=45°,
∴∠A=180°﹣∠ACB﹣∠B=25°.
故答案为25°.
【点评】本题考查了等腰三角形的性质和三角形内角和定理,得到∠B和∠ACB的度数是解题的关键.
三、解答题
10.【解析】(1)直接利用圆周角定理结合垂直于同一直线的两条直线互相平行得出即可;
(2)利用平行弦之间所夹的弧相等进而得出答案.
(1)证明:∵BE是⊙O的直径,
∴∠BAE=90°,即AE⊥AB
又∵AB⊥CD,
∴AE∥CD;
(2)解:∵AE∥CD,
∴=,
∴AC=DE=3.
【点评】此题主要考查了圆周角定理以及平行弦之间的关系,正确应用圆周角定理是解题关键.
11.【解析】连结AE,如图,根据圆周角定理,由=得∠DAE=∠BAE,由AB为直径得∠AEB=90°,根据等腰三角形的判定方法即可得△ABC为等腰三角形;
证明:连结AE,如图,
( http: / / www.21cnjy.com )
∵=,∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∴△ABC为等腰三角形.
【点评】本题考查了圆周角定理:在同 ( http: / / www.21cnjy.com )圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质和勾股定理.
12.【解析】(1)连结OQ,如图1,由PQ∥AB,OP⊥PQ得到OP⊥AB,在Rt△OBP中,利用正切定义可计算出OP=3tan30°=,然后在Rt△OPQ中利用勾股定理可计算出PQ=;
(2)连结OQ,如图2,在Rt△OPQ中,根据勾股定理得到PQ=,则当OP的长最小时,PQ的长最大,根据垂线段最短得到OP⊥BC,则OP=OB=,所以PQ长的最大值=.
解:(1)连结OQ,如图1,
( http: / / www.21cnjy.com )
∵PQ∥AB,OP⊥PQ,
∴OP⊥AB,
在Rt△OBP中,∵tan∠B=,
∴OP=3tan30°=,
在Rt△OPQ中,∵OP=,OQ=3,
∴PQ==;
(2)连结OQ,如图2,
( http: / / www.21cnjy.com )
在Rt△OPQ中,PQ==,
当OP的长最小时,PQ的长最大,
此时OP⊥BC,则OP=OB=,
∴PQ长的最大值为=.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了勾股定理和解直角三角形.
13.【解析】(1)由圆O的圆周角∠AC ( http: / / www.21cnjy.com )B=90°,根据90°的圆周角所对的弦为圆的直径得到AD为圆O的直径,再根据直径所对的圆周角为直角可得三角形ADE为直角三角形,又AD是△ABC的角平分线,可得一对角相等,而这对角都为圆O的圆周角,根据同圆或等圆中,相等的圆周角所对的弦相等可得CD=ED,利用HL可证明直角三角形ACD与AED全等,根据全等三角形的对应边相等即可得得出AC=AE,进而得出BE的长;
(2)由第一问的结论AE=AC,用A ( http: / / www.21cnjy.com )B﹣AE可求出EB的长,再由(1)∠AED=90°,得到DE与AB垂直,可得三角形BDE为直角三角形,设DE=CD=x,用CB﹣CD表示出BD=12﹣x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为CD的长,在直角三角形ACD中,由AC及CD的长,利用勾股定理即可求出AD的长,进而得出外接圆半径.
解:(1)∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),
∴∠AED=90°(直径所对的圆周角为直角),
又AD是△ABC的角平分线(已知),
∴∠CAD=∠EAD(角平分线定义),
∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE(全等三角形的对应边相等);
∵△ABC为直角三角形,且AC=5,CB=12,
∴根据勾股定理得:AB==13,
∴BE=13﹣AC=13﹣5=8;
(2)由(1)得到∠AED=90°,则有∠BED=90°,
设CD=DE=x,则DB=BC﹣CD=12﹣x,EB=AB﹣AE=AB﹣AC=13﹣5=8,
在Rt△BED中,根据勾股定理得:BD2=BE2+ED2,
即(12﹣x)2=x2+82,
解得:x=,
∴CD=,又AC=5,△ACD为直角三角形,
∴根据勾股定理得:AD==,
根据AD是△ACD外接圆直径,
∴△ACD外接圆的半径为:×=.
【点评】此题考查了圆周角定理,勾股定理 ( http: / / www.21cnjy.com ),以及全等三角形的判定与性质,利用了转化的思想,本题的思路为:根据圆周角定理得出直角,利用勾股定理构造方程来求解,从而得到解决问题的目的,灵活运用圆周角定理及勾股定理是解本题的关键.
14.【解析】(1)连结PB,如图1,根据圆周角定理得到∠APB=90°,根据圆心角、弧、弦的关系由=得到PA=PB,则△PAB为等腰直角三角形,所以PA=AB=;
(2)连结BC、BP、PO,OP交BC于H,根据圆周角定理得,∠APB=∠ACB=90°,再根据垂径定理得OP⊥BC,则OH=AC=3,在Rt△OBH中利用勾股定理计算出BH=4,在Rt△PBH中计算出PB=2,然后在Rt△ABP中利用勾股定理可计算出PB=4.
解:(1)连结PB,如图1,
( http: / / www.21cnjy.com )
∵AB是⊙O的直径,
∴∠APB=90°,
∵点P是的中点,
∴=,
∴PA=PB,
∴△PAB为等腰直角三角形,
∴PA=AB=×10=5;
(2)连结BC、BP、PO,OP交BC于H,如图2,
( http: / / www.21cnjy.com )
∵AB是⊙O的直径,
∴∠APB=∠ACB=90°,
∵点P是的中点,
∴OP⊥BC,
∴BH=CH,
∴OH=AC=3,
在Rt△OBH中,∵OB=5,OH=3,
∴BH==4,
在Rt△PBH中,∵PH=OP﹣OH=5﹣3=2,BH=4,
∴PB==2,
在Rt△ABP中,∵AB=10,PB=2,
∴PA==4.
【点评】本题考查了圆周角定理及其推论,也考查了勾股定理.
15.【解析】(1)根据圆周角定理和勾股定理得到AB=AC;
(2)在AE上截取AF=BP,连结AC、BC、FC、PC,如图2,由=得到AC=BC,再证明△CAF≌△CBP,得到CF=CP,由于弦CD⊥PA于E,根据等腰三角形的性质得EF=EP,于是有AE=PB+PE.
解:(1)AB=AC.理由如下:
∵AB为直径,C为的中点,
∴△ABC是等腰直角三角形,
∴AB=AC;
(2)AE=PB+PE.理由如下:
在AE上截取AF=BP,连结AC、BC、FC、PC,如图,
( http: / / www.21cnjy.com )
∵C为劣弧的中点,即=,
∴AC=BC,
在△CAF和△CBP中
,
∴△CAF≌△CBP,
∴CF=CP,
∵弦CD⊥PA于E,
∴EF=EP,
∴AE=AF+EF=PB+PE.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了全等三角形的判定与性质.
A
C
B
O
同课章节目录
