【多媒体导学案】人教版数学九年级上册第24章第6课时《圆内接四边形》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第6课时《圆内接四边形》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 159.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 00:00:00 | ||
图片预览



文档简介
一、学习目标 知道什么是圆内接多边形和多边形的外接圆;理解圆内接四边形的性质;会利用圆内接四边形的性质进行简单计算和证明.
二、知识回顾 圆周角定义: 顶点在圆上 ,并且 两边都和圆相交 的角叫圆周角.在同圆或等圆中, 同弧或等弧 所对的圆周角相等,都等于该弧所对的 圆心角 的一半,相等的圆周角所对的 弧 相等.半圆或直径所对的 圆周角 都相等,都等于 90° ,90°的圆周角所对的弦是圆的 直径 .
三、新知讲解 1.圆内接四边形如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.这个圆叫做四边形的外接圆.2.圆内接四边形的性质性质1:圆内接四边形的对角互补. ※性质2:圆内接四边形的任何一个外角都等于它的内对角.几何语言:∵四边形ABCD内接于圆O,∴∠A+∠C=180°,∠B+∠ADC=180°,∠B=∠1. ( http: / / www.21cnjy.com )
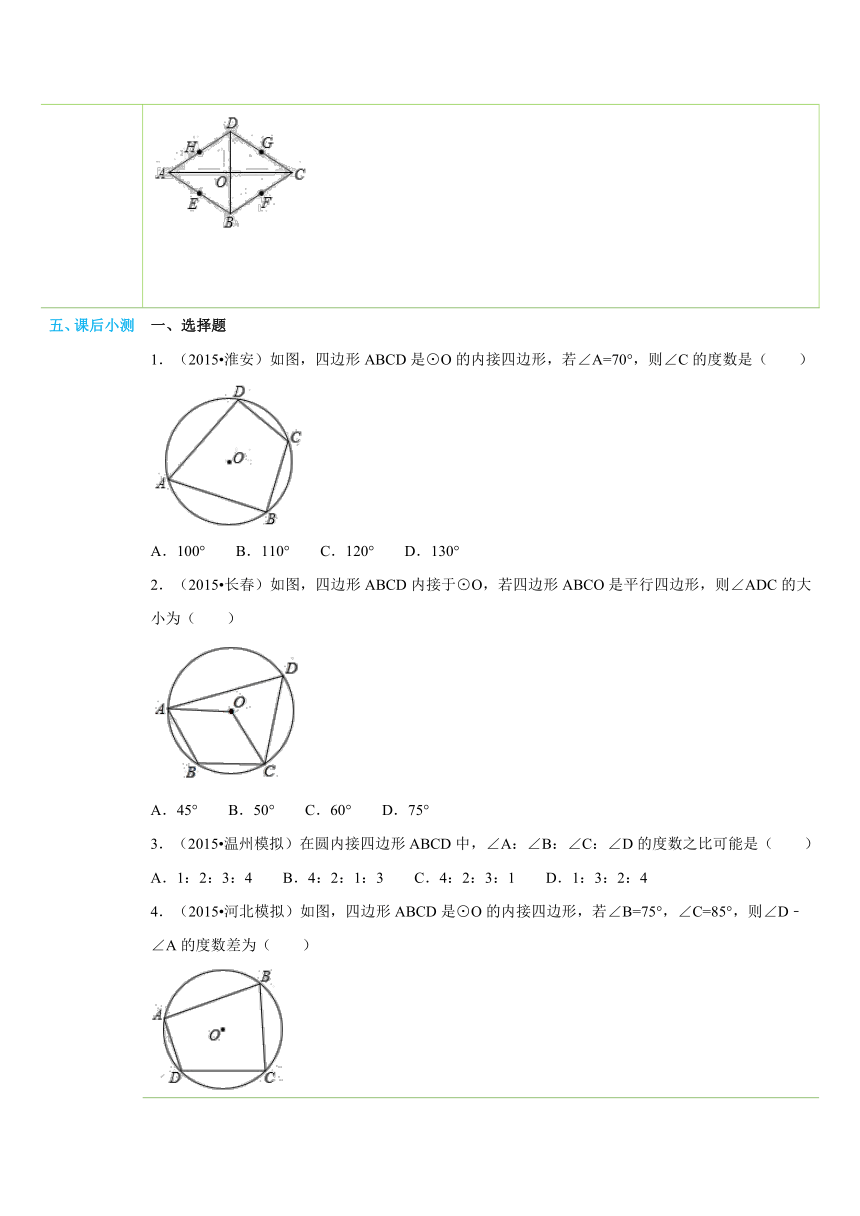
四、典例探究 扫一扫,有惊喜哦!1.已知圆内接四边形求角度【例1】(2015 邵阳)如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( ) ( http: / / www.21cnjy.com )A.80° B.100° C.60° D.40°总结:当四边形的四个顶点都在圆上时,这个四边形叫做圆内接四边形. 常利用“圆内接四边形的对角互补”解决圆中角度问题.解题时观察图形,分清四边形的外角和内对角的位置,不要受背景的干扰.练1.(2012秋 富顺县校级月考)如图,△ABC内接于⊙O,AB=AC,P是上一点,∠BAC=30°,则∠APB=( ) ( http: / / www.21cnjy.com )A.105° B.110° C.115° D.120°2.求证四点共圆【例2】已知在四边形ABCD中,∠B+∠D=180°,能否画出一个圆,使它的四个顶点都在同一个圆上? ( http: / / www.21cnjy.com )总结:任意一个三角形都有外接圆,因为不在同一直线上的三点必定共圆.并非任意四边形都有外接圆,只有对角互补的四边形有外接圆,或者说对角互补的四边形的四个顶点共圆.常见的有外接圆的四边形:正方形、矩形、菱形、等腰梯形.练2.(2014秋 如皋市校级月考)如图 ( http: / / www.21cnjy.com ),菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是它的四条边AB、BC、CD、DA的中点,E、F、G、H四个点共圆吗?(友情提示:要找到一点,证明这四点到找到的这点(圆心)的距离相等即可) ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2015 淮安)如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( ) ( http: / / www.21cnjy.com )A.100° B.110° C.120° D.130°2.(2015 长春)如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( ) ( http: / / www.21cnjy.com )A.45° B.50° C.60° D.75°3.(2015 温州模拟)在圆内接四边形ABCD中,∠A:∠B:∠C:∠D的度数之比可能是( )A.1:2:3:4 B.4:2:1:3 C.4:2:3:1 D.1:3:2:44.(2015 河北模拟)如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D﹣∠A的度数差为( ) ( http: / / www.21cnjy.com )A.10° B.15° C.20° D.25°5.(2014秋 瓯海区校级期中)圆内接四边形ABCD的四个内角之比可能是( )A.1:2:3:4 B.1:3:4:5 C.2:3:4:5 D.2:3:5:46.(2011 浙江模拟)每一个三角形都有一个外接圆,但一个四边形不一定有外接圆.下面哪个四边形没有外接圆?( )A.矩形(非正方形) B.菱形(非正方形) C.正方形 D.等腰梯形7.(2010 静海县一模)已知下列图形:①平行四边形;②矩形;③菱形;④三角形;⑤等腰梯形.其中一定有外接圆的是( )A.2个 B.3个 C.4个 D.5个8.(2011秋 市中区校级期末)如果四边形ABCD是⊙O的内接四边形,那么下列结论不正确的是( )A.∠A+∠B=180° B.∠A+∠C=180° C.∠B+∠D=180° D.∠A+∠B+∠C>∠D二、填空题9.(2015 青岛)如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F= . ( http: / / www.21cnjy.com )10.(2015 泉州)如图,在⊙O的内接四边形ABCD中,点E在DC的延长线上.若∠A=50°,则∠BCE= . ( http: / / www.21cnjy.com )11.(2015 玄武区二模)如图,四边形 ( http: / / www.21cnjy.com )ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,∠ABO=30°,则∠D= °. ( http: / / www.21cnjy.com )12.(2002 南宁)圆内接四边形ABCD中,∠A、∠B、∠C的度数的比是1:2:3,那么这四边形最大角的度数是 度.三、解答题13.根据图中所给信息,分别解出图1和图2中未知数x、y的值. ( http: / / www.21cnjy.com )大家知道:任意四个点不能确定一个圆,但是有 ( http: / / www.21cnjy.com )些特殊四边形的四个顶点在同一个圆上,请说出这些特殊的四边形,并研究这些四边形的四个内角之间有什么特殊的关系.15.如图,在矩形ABCD中,对角线AC和BD交于点O,试说明点A、B、C、D在同一个圆上,并画出这个圆. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据圆内接四边形的性质求得∠ABC=40°,利用圆周角定理,得∠AOC=2∠B=80°.
解:∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABC=180°﹣140°=40°.
∴∠AOC=2∠ABC=80°.
故选A.
点评:此题主要考查了圆周角定理以及圆内接四边形的性质,得出∠B的度数是解题关键.
练1.【解析】首先根据等腰三角形的性质计算出∠C= =75°,再根据圆内接四边形的对角互补可得答案.
解:∵AB=AC,
∴∠C=∠B,
∵∠BAC=30°,
∴∠C= =75°,
∴∠APB=180°﹣75°=105°,
故选:A.
点评:此题主要考查了圆内接四边形的性质,关键是掌握:①圆内接四边形的对角互补.②圆内接四边形的对边和相等.
【例2】【解析】根据不在同 ( http: / / www.21cnjy.com )一直线上的三点确定一个圆,不妨设A、B、C三点确定一个圆,则点D与圆的位置关系有三种:在圆外,在圆上、在圆内,如果能排除点D在圆外或圆内,则点D必在圆上.
解:能画出一个圆,使它的四个顶点都在同一个圆上.
设△ABC的外接圆为⊙O,对点D的位置分情况讨论:在⊙O上、在⊙O外或在⊙O内.
(1)如果点D在⊙O外,设E是AD与⊙O的交点,连接CE,如图,
( http: / / www.21cnjy.com )
则有∠B+∠AEC=180°,而∠B+∠D=180°,所以∠D=∠AEC,
这与“三角形外角大于任意不相邻的内角”矛盾,
故点D不可能在圆外.
(2)如果点D在⊙O内,延长AD交圆于点E,连接CE,如图,
( http: / / www.21cnjy.com )
则∠B+∠E=180°,而∠B+∠ADC=180°,故∠E=∠ADC,
同样与“三角形外角大于任意不相邻的内角”矛盾,
所以点D不可能在⊙O内.
综上,点D只能在⊙O上,
即在四边形ABCD中,∠B+∠D=180°,能画出一个圆,使它的四个顶点都在同一个圆上.
点评:本题考查了圆内接四边形的性质和判 ( http: / / www.21cnjy.com )定条件.圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来.在应用时要注意是对角互补,而不是邻角互补.
练2.【解析】由菱形的性质可得到菱 ( http: / / www.21cnjy.com )形被分成四个全等的直角三角形,再利用直角三角形斜边上的中线等于斜边的一半,可得四个中点到对角线的交点的距离相等.
解:E、F、G、H四个点共圆.
证明:连接OE、OF、OG、OH;
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,DB⊥AC,
∵E、F、G、H分别是各边的中点,
∴,,,;
∴OE=OF=OG=OH,
∴E、F、G、H四个点都在以O为圆心、OE长为半径的圆上.
点评:熟练掌握菱形的性质.明确判断几个点共圆就是要证明这几个点到某个点的距离相等.
课后小测答案:
一、选择题
1.解:∵四边形ABCD是⊙O的内接四边形,
∴∠C+∠A=180°,
∴∠A=180°﹣70°=110°.
故选B.
2.解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形OADC是平行四边形,
∴∠ADC=∠AOC;
∵∠ADC=β,∠AOC=α;
而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故选C.
3.解:∵圆的内接四边形对角互补,
∴∠A+∠C=∠B+∠D=180°,
∴∠A:∠B:∠C:∠D的可能的值是4:2:1:3.
故选:B.
4.解:∵四边形ABCD是⊙O的内接四边形,
∴∠B+∠D=180°,∠C+∠A=180°,
∵∠B=75°,∠C=85°,
∴∠D=105°,∠A=95°,
∴∠D﹣∠A=10°,
故选:A.
5.解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°.
∴圆内接四边形ABCD的四个内角之比可能是:2:3:5:4.
故选D.
6.解:由于圆内接四边形的对角互补,因此只有A、C、D选项的四边形符合这个条件,故选B.
7.解:根据有外接圆的条件,四边形必须对角互补,
∴只有矩形、等腰梯形有外接圆,
∵三角形都有外接圆,
故②④⑤一定有外接圆.
故选:B.
8.解:如图所示:
( http: / / www.21cnjy.com )
∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,∠B+∠D=180°,故B、C正确;
∴∠A+∠C+∠B>180°,∠D<180°,
∴∠A+∠B+∠C>∠D,故D选项正确,
∵∠A与∠B不是相对的角,
∴∠A与∠B的和不能确定,故A选项错误.
故选A.
二、填空题
9.解:∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
故答案为40°.
10.解:∵四边形ABCD内接于⊙O,
∴∠BCE=∠A=50°.
故答案为50°.
11.解:连结OC,如图,
( http: / / www.21cnjy.com )
∠BOC=2∠CAB=2×36°=72°,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC=(180°﹣∠BOC)=(180°﹣72°)=54°,
∴∠ABC=∠OBA+∠OBC=30°+54°=84°,
∵∠D+∠ABC=180°,
∴∠D=180°﹣84°=96°.
故答案为96.
12.解:设∠A=x,则∠B=2x,∠C=3x
因为四边形ABCD为圆内接四边形
所以∠A+∠C=180°
即:x+3x=180
x=45°,则∠A=45°,∠B=90°,∠C=135°
所以∠D=90°
所以这个四边形的最大角的度数为135度.
三、解答题
13.解:图1,根据题意可得∠DFE=∠BFC=∠BAD=y,∠FDE=∠ABE=x,
∴x+y+30°=180°,x=50°+y,解得:x=100°,y=50°,
图2,同理可得x+y+35°=180°,x=54°+y,解得:x=99.5°,y=45.5°.
14.解:∵矩形、正方形的对角线相等且互相平分,
∴四个顶点到对角线交点距离相等,
∴矩形、正方形的四个顶点可在同一个圆上;
四个顶点在同一个圆上的四边形的对角互补.
15.解:∵四边形ABDC是矩形,
∴AD=BC,OA=OD,OB=OC,
∴OA=OB=OC=OD,
即A、B、C、D在以点O为圆心、OA为半径的圆上.
( http: / / www.21cnjy.com )
二、知识回顾 圆周角定义: 顶点在圆上 ,并且 两边都和圆相交 的角叫圆周角.在同圆或等圆中, 同弧或等弧 所对的圆周角相等,都等于该弧所对的 圆心角 的一半,相等的圆周角所对的 弧 相等.半圆或直径所对的 圆周角 都相等,都等于 90° ,90°的圆周角所对的弦是圆的 直径 .
三、新知讲解 1.圆内接四边形如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.这个圆叫做四边形的外接圆.2.圆内接四边形的性质性质1:圆内接四边形的对角互补. ※性质2:圆内接四边形的任何一个外角都等于它的内对角.几何语言:∵四边形ABCD内接于圆O,∴∠A+∠C=180°,∠B+∠ADC=180°,∠B=∠1. ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.已知圆内接四边形求角度【例1】(2015 邵阳)如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( ) ( http: / / www.21cnjy.com )A.80° B.100° C.60° D.40°总结:当四边形的四个顶点都在圆上时,这个四边形叫做圆内接四边形. 常利用“圆内接四边形的对角互补”解决圆中角度问题.解题时观察图形,分清四边形的外角和内对角的位置,不要受背景的干扰.练1.(2012秋 富顺县校级月考)如图,△ABC内接于⊙O,AB=AC,P是上一点,∠BAC=30°,则∠APB=( ) ( http: / / www.21cnjy.com )A.105° B.110° C.115° D.120°2.求证四点共圆【例2】已知在四边形ABCD中,∠B+∠D=180°,能否画出一个圆,使它的四个顶点都在同一个圆上? ( http: / / www.21cnjy.com )总结:任意一个三角形都有外接圆,因为不在同一直线上的三点必定共圆.并非任意四边形都有外接圆,只有对角互补的四边形有外接圆,或者说对角互补的四边形的四个顶点共圆.常见的有外接圆的四边形:正方形、矩形、菱形、等腰梯形.练2.(2014秋 如皋市校级月考)如图 ( http: / / www.21cnjy.com ),菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是它的四条边AB、BC、CD、DA的中点,E、F、G、H四个点共圆吗?(友情提示:要找到一点,证明这四点到找到的这点(圆心)的距离相等即可) ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2015 淮安)如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( ) ( http: / / www.21cnjy.com )A.100° B.110° C.120° D.130°2.(2015 长春)如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( ) ( http: / / www.21cnjy.com )A.45° B.50° C.60° D.75°3.(2015 温州模拟)在圆内接四边形ABCD中,∠A:∠B:∠C:∠D的度数之比可能是( )A.1:2:3:4 B.4:2:1:3 C.4:2:3:1 D.1:3:2:44.(2015 河北模拟)如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D﹣∠A的度数差为( ) ( http: / / www.21cnjy.com )A.10° B.15° C.20° D.25°5.(2014秋 瓯海区校级期中)圆内接四边形ABCD的四个内角之比可能是( )A.1:2:3:4 B.1:3:4:5 C.2:3:4:5 D.2:3:5:46.(2011 浙江模拟)每一个三角形都有一个外接圆,但一个四边形不一定有外接圆.下面哪个四边形没有外接圆?( )A.矩形(非正方形) B.菱形(非正方形) C.正方形 D.等腰梯形7.(2010 静海县一模)已知下列图形:①平行四边形;②矩形;③菱形;④三角形;⑤等腰梯形.其中一定有外接圆的是( )A.2个 B.3个 C.4个 D.5个8.(2011秋 市中区校级期末)如果四边形ABCD是⊙O的内接四边形,那么下列结论不正确的是( )A.∠A+∠B=180° B.∠A+∠C=180° C.∠B+∠D=180° D.∠A+∠B+∠C>∠D二、填空题9.(2015 青岛)如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F= . ( http: / / www.21cnjy.com )10.(2015 泉州)如图,在⊙O的内接四边形ABCD中,点E在DC的延长线上.若∠A=50°,则∠BCE= . ( http: / / www.21cnjy.com )11.(2015 玄武区二模)如图,四边形 ( http: / / www.21cnjy.com )ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,∠ABO=30°,则∠D= °. ( http: / / www.21cnjy.com )12.(2002 南宁)圆内接四边形ABCD中,∠A、∠B、∠C的度数的比是1:2:3,那么这四边形最大角的度数是 度.三、解答题13.根据图中所给信息,分别解出图1和图2中未知数x、y的值. ( http: / / www.21cnjy.com )大家知道:任意四个点不能确定一个圆,但是有 ( http: / / www.21cnjy.com )些特殊四边形的四个顶点在同一个圆上,请说出这些特殊的四边形,并研究这些四边形的四个内角之间有什么特殊的关系.15.如图,在矩形ABCD中,对角线AC和BD交于点O,试说明点A、B、C、D在同一个圆上,并画出这个圆. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】根据圆内接四边形的性质求得∠ABC=40°,利用圆周角定理,得∠AOC=2∠B=80°.
解:∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABC=180°﹣140°=40°.
∴∠AOC=2∠ABC=80°.
故选A.
点评:此题主要考查了圆周角定理以及圆内接四边形的性质,得出∠B的度数是解题关键.
练1.【解析】首先根据等腰三角形的性质计算出∠C= =75°,再根据圆内接四边形的对角互补可得答案.
解:∵AB=AC,
∴∠C=∠B,
∵∠BAC=30°,
∴∠C= =75°,
∴∠APB=180°﹣75°=105°,
故选:A.
点评:此题主要考查了圆内接四边形的性质,关键是掌握:①圆内接四边形的对角互补.②圆内接四边形的对边和相等.
【例2】【解析】根据不在同 ( http: / / www.21cnjy.com )一直线上的三点确定一个圆,不妨设A、B、C三点确定一个圆,则点D与圆的位置关系有三种:在圆外,在圆上、在圆内,如果能排除点D在圆外或圆内,则点D必在圆上.
解:能画出一个圆,使它的四个顶点都在同一个圆上.
设△ABC的外接圆为⊙O,对点D的位置分情况讨论:在⊙O上、在⊙O外或在⊙O内.
(1)如果点D在⊙O外,设E是AD与⊙O的交点,连接CE,如图,
( http: / / www.21cnjy.com )
则有∠B+∠AEC=180°,而∠B+∠D=180°,所以∠D=∠AEC,
这与“三角形外角大于任意不相邻的内角”矛盾,
故点D不可能在圆外.
(2)如果点D在⊙O内,延长AD交圆于点E,连接CE,如图,
( http: / / www.21cnjy.com )
则∠B+∠E=180°,而∠B+∠ADC=180°,故∠E=∠ADC,
同样与“三角形外角大于任意不相邻的内角”矛盾,
所以点D不可能在⊙O内.
综上,点D只能在⊙O上,
即在四边形ABCD中,∠B+∠D=180°,能画出一个圆,使它的四个顶点都在同一个圆上.
点评:本题考查了圆内接四边形的性质和判 ( http: / / www.21cnjy.com )定条件.圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来.在应用时要注意是对角互补,而不是邻角互补.
练2.【解析】由菱形的性质可得到菱 ( http: / / www.21cnjy.com )形被分成四个全等的直角三角形,再利用直角三角形斜边上的中线等于斜边的一半,可得四个中点到对角线的交点的距离相等.
解:E、F、G、H四个点共圆.
证明:连接OE、OF、OG、OH;
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,DB⊥AC,
∵E、F、G、H分别是各边的中点,
∴,,,;
∴OE=OF=OG=OH,
∴E、F、G、H四个点都在以O为圆心、OE长为半径的圆上.
点评:熟练掌握菱形的性质.明确判断几个点共圆就是要证明这几个点到某个点的距离相等.
课后小测答案:
一、选择题
1.解:∵四边形ABCD是⊙O的内接四边形,
∴∠C+∠A=180°,
∴∠A=180°﹣70°=110°.
故选B.
2.解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形OADC是平行四边形,
∴∠ADC=∠AOC;
∵∠ADC=β,∠AOC=α;
而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故选C.
3.解:∵圆的内接四边形对角互补,
∴∠A+∠C=∠B+∠D=180°,
∴∠A:∠B:∠C:∠D的可能的值是4:2:1:3.
故选:B.
4.解:∵四边形ABCD是⊙O的内接四边形,
∴∠B+∠D=180°,∠C+∠A=180°,
∵∠B=75°,∠C=85°,
∴∠D=105°,∠A=95°,
∴∠D﹣∠A=10°,
故选:A.
5.解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°.
∴圆内接四边形ABCD的四个内角之比可能是:2:3:5:4.
故选D.
6.解:由于圆内接四边形的对角互补,因此只有A、C、D选项的四边形符合这个条件,故选B.
7.解:根据有外接圆的条件,四边形必须对角互补,
∴只有矩形、等腰梯形有外接圆,
∵三角形都有外接圆,
故②④⑤一定有外接圆.
故选:B.
8.解:如图所示:
( http: / / www.21cnjy.com )
∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,∠B+∠D=180°,故B、C正确;
∴∠A+∠C+∠B>180°,∠D<180°,
∴∠A+∠B+∠C>∠D,故D选项正确,
∵∠A与∠B不是相对的角,
∴∠A与∠B的和不能确定,故A选项错误.
故选A.
二、填空题
9.解:∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
故答案为40°.
10.解:∵四边形ABCD内接于⊙O,
∴∠BCE=∠A=50°.
故答案为50°.
11.解:连结OC,如图,
( http: / / www.21cnjy.com )
∠BOC=2∠CAB=2×36°=72°,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC=(180°﹣∠BOC)=(180°﹣72°)=54°,
∴∠ABC=∠OBA+∠OBC=30°+54°=84°,
∵∠D+∠ABC=180°,
∴∠D=180°﹣84°=96°.
故答案为96.
12.解:设∠A=x,则∠B=2x,∠C=3x
因为四边形ABCD为圆内接四边形
所以∠A+∠C=180°
即:x+3x=180
x=45°,则∠A=45°,∠B=90°,∠C=135°
所以∠D=90°
所以这个四边形的最大角的度数为135度.
三、解答题
13.解:图1,根据题意可得∠DFE=∠BFC=∠BAD=y,∠FDE=∠ABE=x,
∴x+y+30°=180°,x=50°+y,解得:x=100°,y=50°,
图2,同理可得x+y+35°=180°,x=54°+y,解得:x=99.5°,y=45.5°.
14.解:∵矩形、正方形的对角线相等且互相平分,
∴四个顶点到对角线交点距离相等,
∴矩形、正方形的四个顶点可在同一个圆上;
四个顶点在同一个圆上的四边形的对角互补.
15.解:∵四边形ABDC是矩形,
∴AD=BC,OA=OD,OB=OC,
∴OA=OB=OC=OD,
即A、B、C、D在以点O为圆心、OA为半径的圆上.
( http: / / www.21cnjy.com )
同课章节目录
