【多媒体导学案】人教版数学九年级上册第24章第7课时《点和圆的位置关系》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第7课时《点和圆的位置关系》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 00:00:00 | ||
图片预览



文档简介
一、学习目标 1.掌握点和圆的三种位置关系,能够用数量关系来判断点和圆的位置关系;2.掌握不在同一条直线上的三点确定一个圆,能画出三角形的外接圆,求出特殊三角形的外接圆的半径;3.了解反证法,会用反证法证明;4.渗透方程思想、分类讨论思想.
二、知识回顾 1.(1)在一个平面内,线段OA绕它的一个端点O旋转一周,则另一个端点A所形成的封闭曲线叫做 圆 ;(2)圆心为O,半径为r的圆可以看成是所有到定点O的距离等于 r 的点组成的图形.(3)圆上所有的点到圆心的距离都等于 半径 .2.请你画图并想一想:当点分别在圆外和圆内时,点到圆心的距离与半径的关系分别怎样呢?经过画图可知,圆外的点到圆心的距离 大于 半径,圆内的点到圆心的距离 小于 半径.
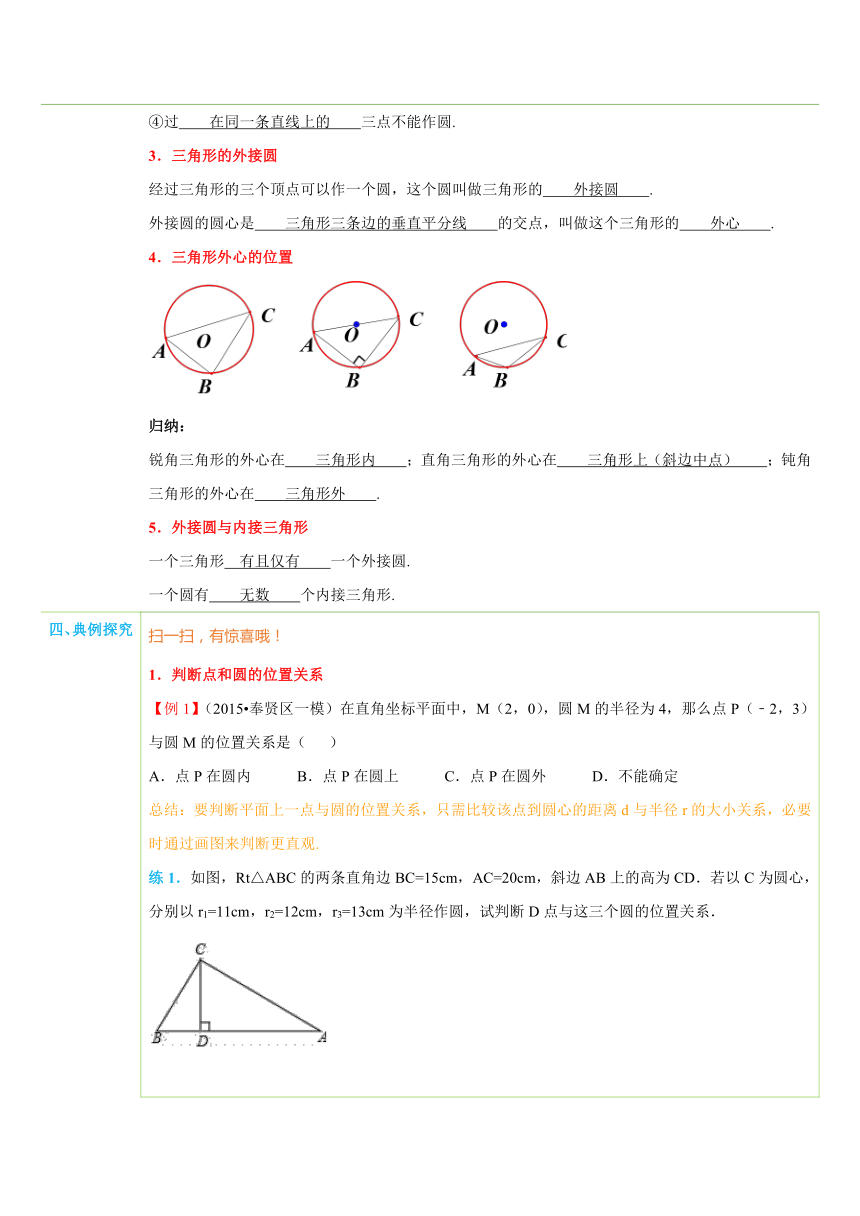
三、新知讲解 1.点和圆的位置关系设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r ;②点P在圆上 d=r ;③点P在 圆内 d<r.点和圆的位置关系与圆心到点的距离d与半径r的关系用表格表示如下: ( http: / / www.21cnjy.com )2.作圆①过一点可作 无数 个圆;②过两点可作 无数 个圆;③过不在同一条直线上的三点可确定 一个 圆;④过 在同一条直线上的 三点不能作圆.3.三角形的外接圆经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的 外接圆 .外接圆的圆心是 三角形三条边的垂直平分线 的交点,叫做这个三角形的 外心 .4.三角形外心的位置 ( http: / / www.21cnjy.com )归纳:锐角三角形的外心在 三角形内 ;直角三角形的外心在 三角形上(斜边中点) ;钝角三角形的外心在 三角形外 .5.外接圆与内接三角形一个三角形 有且仅有 一个外接圆.一个圆有 无数 个内接三角形.
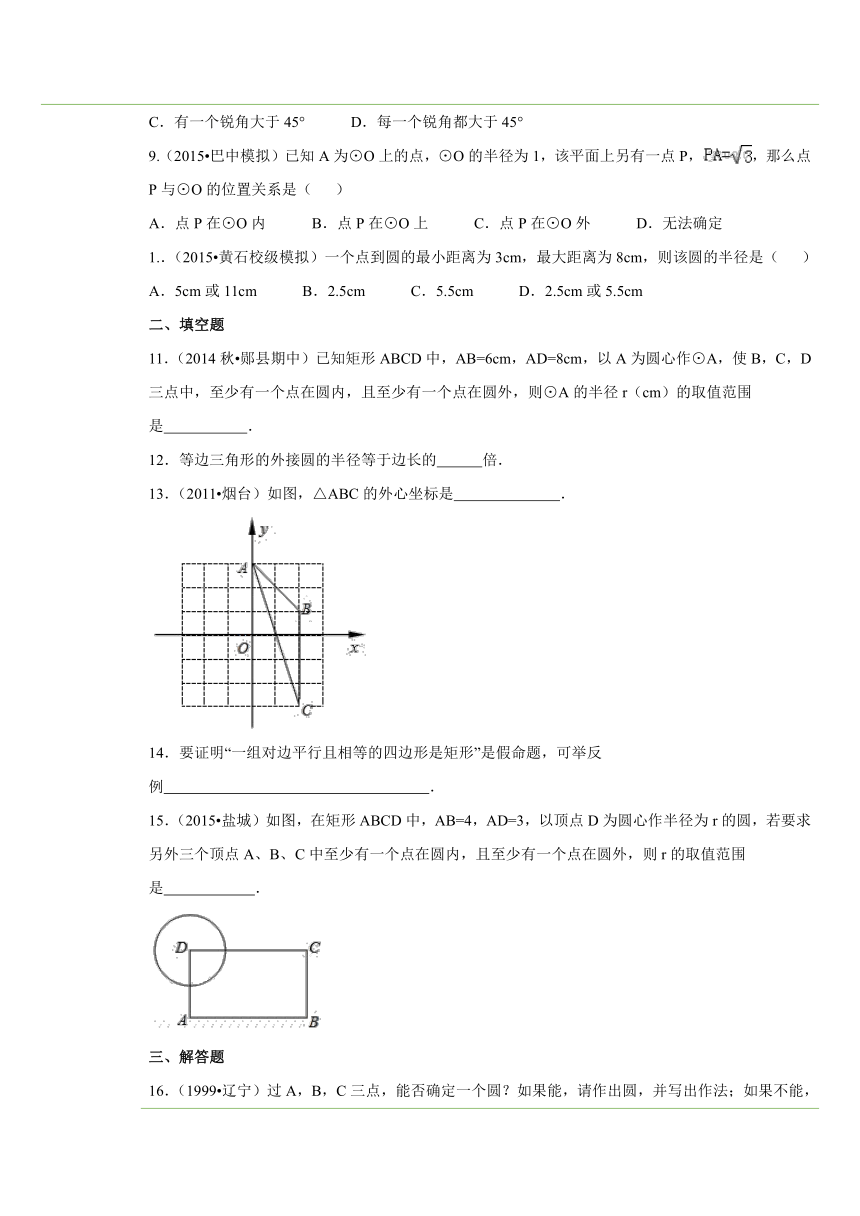
四、典例探究 扫一扫,有惊喜哦!1.判断点和圆的位置关系【例1】(2015 奉贤区一模)在直角坐标平面中,M(2,0),圆M的半径为4,那么点P(﹣2,3)与圆M的位置关系是( )A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定总结:要判断平面上一点与圆的位置关系,只需比较该点到圆心的距离d与半径r的大小关系,必要时通过画图来判断更直观.练1.如图,Rt△ABC的两条直角边BC ( http: / / www.21cnjy.com )=15cm,AC=20cm,斜边AB上的高为CD.若以C为圆心,分别以r1=11cm,r2=12cm,r3=13cm为半径作圆,试判断D点与这三个圆的位置关系. ( http: / / www.21cnjy.com )2.利用点和圆的位置关系求半径【例2】(2014秋 余姚市校级月考)若⊙O所在平面内一点P到⊙O上的点的最大距离为7,最小距离为3,则此圆的半径为( )A.5 B.2 C.10或4 D.5或2总结:平面内一点没有指明在圆内还是圆外时,注意分类讨论这两种情况。连接平面内一点与圆心并延长,可以找到平面内一点与圆上一点的最长距离和最短距离.练2.在Rt△ABC中,已知∠C=90°,BC=3,AC=4,以点B为圆心,3为半径作圆B,则:(1)AB与AC的中点D,E与圆B有怎样的位置关系?(2)若要让点A和点C有且只有一个点在圆B内,则圆B的半径应满足什么条件?3.求特殊三角形外接圆的半径【例3】若直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .总结:特殊三角形的外接圆半径求解有规律:(1)直角三角形外接圆的直径等于斜边长;(2)边长为的等边三角形外接圆的半径等于;(3)求等腰三角形外接圆的半径,先作底边的高,构造直角三角形,结合勾股定理、垂径定理求解.练3.若顶角为120°的等腰三角形的腰长为5cm,则它的外接圆的直径为 .4.用反证法证明【例4】用反证法证明:一个圆只有一个圆心.总结:反证法的步骤是:假设结论不成立;从假设出发推出矛盾;假设不成立,则结论成立.练4.用反证法证明:圆内不是直径的两条弦不能互相平分.
五、课后小测 一、选择题1.(2011秋 市中区校级期末)确定一个圆的条件是( )A.两个点确定一个圆 B.三个点确定一个圆C.四个点确定一个圆 D.不共线的三个点确定一个圆2.(2013秋 雁塔区校级月考)下列条件中,能确定圆的是( )A.以已知点O为圆心 B.以1cm长为半径C.经过已知点A,且半径为2cm D.以点O为圆心,1cm为半径3.(2014 奉贤区一模)关于半径为5的圆,下列说法正确的是( )A.若有一点到圆心的距离为5,则该点在圆外B.若有一点在圆外,则该点到圆心的距离不小于5C.圆上任意两点之间的线段长度不大于10D.圆上任意两点之间的部分可以大于10π4.(2011秋 京口区校级期末)三角形外接圆的圆心为( )A.三条高的交点 B.三条角平分线的交点C.三条垂直平分线的交点 D.三条中线的交点5.(2010秋 崂山区校级期中)有一个三角形的外接圆的圆心在它的某一边上,则这个三角形一定是( )A.等边三角形 B.直角三角形 C.锐角三角形 D.钝角三角形6.(2014秋 瓯海区校级期中)一个三角形的外接圆的圆心在这个三角形的外部,则该三角形一定是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形7.下列说法中,正确的是( )A.三点确定一个圆B.三角形的外心到三角形三边的距离相等C.三角形有且只有一个外接圆D.圆有且只有一个内接三角形8.(2013 北仑区二模)用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设( )A.有一个锐角小于45° B.每一个锐角都小于45°C.有一个锐角大于45° D.每一个锐角都大于45°9.(2015 巴中模拟)已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,,那么点P与⊙O的位置关系是( )A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定1..(2015 黄石校级模拟)一个点到圆的最小距离为3cm,最大距离为8cm,则该圆的半径是( )A.5cm或11cm B.2.5cm C.5.5cm D.2.5cm或5.5cm二、填空题11.(2014秋 郧县期中)已知矩形AB ( http: / / www.21cnjy.com )CD中,AB=6cm,AD=8cm,以A为圆心作⊙A,使B,C,D三点中,至少有一个点在圆内,且至少有一个点在圆外,则⊙A的半径r(cm)的取值范围是 .12.等边三角形的外接圆的半径等于边长的 倍.13.(2011 烟台)如图,△ABC的外心坐标是 . ( http: / / www.21cnjy.com )14.要证明“一组对边平行且相等的四边形是矩形”是假命题,可举反例 .15.(2015 盐城)如图,在矩形ABC ( http: / / www.21cnjy.com )D中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 . ( http: / / www.21cnjy.com )三、解答题16.(1999 辽宁)过A,B,C三点,能否确定一个圆?如果能,请作出圆,并写出作法;如果不能,请用反证法加以证明.17.用反证法证明:(1)△ABC中至多只能有一个角是直角;(2)在同一个圆中,如果两条弦不等,那么它们的弦心距也不等.18.(2013 青岛校级一模)如图,已知A、B两点和线段r.求作:⊙O,使其半径为r,且经过A、B两点.(任作一个即可)结论:
典例探究答案:
【例1】【解析】求得线段MP的长后与圆M的半径比较即可确定正确的选项.
解:∵M(2,0),P(﹣2,3),
∴MP==5,
∵圆M的半径为4,
∴点P在圆外,
故选:C.
【点评】考查了点与圆的位置关系,判断点与圆的位置关系,也就是比较点与圆心的距离和半径的大小关系.
练1.【解析】先根据勾股定理计算出AB=25cm,再利用面积法计算出CD=12cm,然后根据点与圆的位置关系进行判断.
解:∵Rt△ABC的两条直角边BC=15cm,AC=20cm,
∴AB==25cm,
∵BC AC=CD AB,
∴CD==12(cm),
∵所以当以r1=11cm作圆,D点在这个圆的外部;当以r2=12作圆,D点在这个圆上;当以r3=13作圆,D点在这个圆的内部.
【点评】本题考查了点与圆的 ( http: / / www.21cnjy.com )位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r.
【例2】【解析】由于点P与⊙O的位置关系不能确定,故应分两种情况进行讨论.
解:设⊙O的半径为r,
当点P在圆外时,r==2;
当点P在⊙O内时,r==5.
( http: / / www.21cnjy.com )
综上可知此圆的半径为5或2.
故选:D.
【点评】本题考查的是点与圆的位置关系,解答此题时要进行分类讨论,不要漏解.
练2.【考点】点与圆的位置关系.
【解析】(1)先利用勾股定理计算出AB=5,则得到BD=2.5,易得BE>3,然后根据点与圆的位置关系判断D,E与圆B的位置关系;
(2)由于BC=3,BA=5,根据点与圆的位置关系即可确定圆B的半径的范围.
解:(1)如图,
∵∠C=90°,BC=3,AC=4,
∴AB==5,
∵D为AB的中点,
∴BD=2.5,
∴点D在圆B内,
∵BE>BC,即BE>3,
∴点D在圆B外;
(2)设圆B的半径为r,
当3<r<5时,点A和点C有且只有一个点在圆B内.
( http: / / www.21cnjy.com )
【点评】本题考查了点与圆的位置关系:设 ( http: / / www.21cnjy.com )⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r.
【例3】【解析】直角三角形的外接圆 ( http: / / www.21cnjy.com )圆心是斜边的中点,那么半径为斜边的一半,分两种情况:①16为斜边长;②16和12为两条直角边长,由勾股定理易求得此直角三角形的斜边长,进而可求得外接圆的半径.
解:由勾股定理可知:
①当直角三角形的斜边长为16时,这个三角形的外接圆半径为8;
②当两条直角边长分别为16和12,则直角三角形的斜边长==20,
因此这个三角形的外接圆半径为10.
综上所述:这个三角形的外接圆半径等于8或10.
故答案为:10或8.
【点评】本题考查的是直角三角形的外接圆半径,重点在于理解直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的圆.
练3.【解析】作辅助线:连接AO交BC于点D、连接OB,构建等边三角形BAO,然后根据等边三角形及圆的半径与直径的关系解答.
解:连接AO交BC于点D、连接OB.
( http: / / www.21cnjy.com )
∵点O是等腰三角形ABC的外接圆圆心,
∴OA⊥BC,AD是边BC的中垂线,
∴AO是∠BAC的角平分线;
又∠BAC=120°,
∴∠BAO=60°;
又OA=OB(圆的半径),
∴∠BAO=∠OBA=60°(等边对等角),
∴∠BOA=60°(三角形的内角和定理),
∴AB=OA=OB;
又AB=5,
∴⊙O的直径是2OA=10cm.
故答案是:10cm.
【点评】本题主要考查了垂径定理、等边三角形的性质.解此类题目要注意将圆的问题转化成三角形的问题再进行计算.
【例4】【解析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此得出假设与已知定理矛盾,进而得出答案.
证明:假设⊙O有两个圆心O及O′,在圆内任作一弦AB,设弦AB的中点为P,
连结OP,O′P,则OP⊥AB,O′P⊥AB,过直线AB上一点P,同时有两条直线OP,O′P都垂直于AB,与垂线的性质矛盾,
故一个圆只有一个圆心.
( http: / / www.21cnjy.com )
【点评】此题主要考查了反证法,解此题关键要懂得反证法的意义及步骤.
练4.【解析】首先假设圆内不是直径的两条弦AC和BD互相平分于P,进而利用平行四边形的性质以及圆内接四边形的性质得出矛盾,从而得出结论.
证明:假设圆内不是直径的两条弦AC和BD互相平分于P,
∵四边形ABCD的对角线互相平分于P,
∴四边形ABCD是平行四边形,
又∵四边形ABCD是圆内接四边形,
则∠DAB与∠BCD互补,
则∠DAB与∠BCD都是直角(平行四边形对角相等),AC是直径,与假设矛盾,
所以原命题正确.
( http: / / www.21cnjy.com )
【点评】此题主要考查了反证法,正确掌握反证法的一般步骤是解题关键.
课后小测答案:
一、选择题
1.【解析】根据不在同一直线上的三个点确定一个圆判断进而得出答案即可.
解:根据不在同一直线上的三个点确定一个圆,故选项D正确.
故选:D.
【点评】此题主要考查了确定圆的条件,根据不在一条直线上的三点确定一个圆得出是解题关键.
2.【解析】确定一个圆有两个重要因素,一是圆心,而是半径,据此可以得到答案.
解:∵圆心确定,半径确定后才可以确定圆,
∴D选项正确,
故选D
【点评】本题考查了确定圆的条件,确定圆要首先确定圆的圆心,然后也要确定半径.
3.【解析】根据点与圆的位置关系进而分别判断得出即可.
解:A、关于半径为5的圆,有一点到圆心的距离为5,则该点在圆上,故此选项错误;
B、关于半径为5的圆,若有一点在圆外,则该点到圆心的距离大于5,故此选项错误;
C、圆上任意两点之间的线段长度不大于10,此选项正确;
D、圆上任意两点之间的部分不可以大于10π,故此选项错误;
故选:C.
【点评】此题主要考查了点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
①点P在圆外 d>r,②点P在圆上 d=r,③点P在圆内 d<r.
4.【解析】根据三角形外心的性质进行判断.
解:A、三角形三条高的交点是三角形的垂心,故A错误;
B、三角形三条角平分线的交点是三角形的内心,故B错误;
C、由于三角形的外心是三角形三条边的垂直平分线的交点,故C正确;
D、三角形三边中线的交点是三角形的重心,故D错误;
故选:C.
【点评】此题主要考查了三角形外心的性质.注意三角形重心、垂心、内心、外心的区别.
5.【解析】根据三角形的外接圆的圆心在它的某一边上,而这一点到三顶点距离相等,可以判断它的所在位置.
解:三角形的外接圆的圆心到三顶点距离相等,这样的点在三角形边上,
只有这个三角形是直角三角形,并且在斜边上,这样的图形只有直角三角形才符合.
故选:B.
【点评】此题主要考查了三角形的外心与三角形的位置关系只有三种,外接圆的圆心在它的某一边上,只是特殊的直角三角形具备.
6.【解析】根据三角形的外接圆的画 ( http: / / www.21cnjy.com )法得出锐角三角形的外心在三角形的内部,直角三角形的外心在直角三角形斜边的中点上,钝角三角形的外心在三角形的外部,根据以上内容得出即可.
解:∵锐角三角形的外心在三角形的内部,直角三角形的外心在直角三角形斜边的中点上,钝角三角形的外心在三角形的外部,
∴如果一个三角形的外接圆的圆心在这个三角形的外部,则该三角形一定是钝角三角形.
故选:C.
【点评】本题考查了对三角形的外接圆和外心的应用,主要考查学生的理解能力,题目比较好,难度不是很大.
7.【解析】此题应逐项分析,更要牢记“不在同一直线上的三个点确定一个圆”,本题可解.
解:A、正确的是不在同一直线上的三个点确定一个圆,故错误;
B、三角形的外心是边的垂直平分线的交点,因而外心到三个顶点的距离相等,故错误;
C、不在同一直线上的三个点确定一个圆,故正确;
D、圆有无数个内接三角形,故错误.
故选:C.
【点评】正确记忆理解定理是解决本题的关键.
8.【解析】用反证法证明命题的真假,应先按符合题设的条件,假设题设成立,再判断得出的结论是否成立即可.
解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设每一个锐角都大于45°.
故选:D.
【点评】正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理,会运用反证法证明命题的真假.
9.【解析】根据题意可知点P可能在圆外也可能在圆上,也可能在圆内,所以无法确定.
解:∵PA=,⊙O的直径为2
∴点P的位置有三种情况:①在圆外,②在圆上,③在圆内.
故选:D.
【点评】本题考查了圆的认识,做题时注意多种情况的考虑.
10.【解析】点P应分为位于圆的内部位于外部 ( http: / / www.21cnjy.com )两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
解:当点P在圆内时,最近点的距离为3cm,最远点的距离为8cm,则直径是11cm,因而半径是5.5cm;
当点P在圆外时,最近点的距离为3cm,最远点的距离为8m,则直径是5cm,因而半径是2.5cm.
故选:D.
【点评】本题考查了点与圆的位置关系,注意分两种情况进行讨论是解决本题的关键.
二、填空题
11.【解析】要确定点与圆 ( http: / / www.21cnjy.com )的位置关系,主要确定点与圆心的距离与半径的大小关系,本题可由勾股定理等性质算出点与圆心的距离d.则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解:如图:
( http: / / www.21cnjy.com )
在矩形ABCD中AC=AB,==10.
由图可知圆A的半径r的取值范围应大于AD的长,小于对角线AC的长,即6<r<10.
故答案为:6<r<10.
【点评】本题的实质是考查点与圆的位置关系,需要同学们树立数形结合的思想.
12.【解析】等边三角形外接圆的圆心是三条边垂直平分线的交点,根据等边三角形三线合一的性质,同一顶点角平分线与高重合;易得高是边长的倍,继而可得外接圆的半径是角平分线的,所以等边三角形外接圆的半径等于边长的倍.
解:如图,∵△ABC是等边三角形,
( http: / / www.21cnjy.com )
∴设AB=BC=2x,
∵AD⊥BC,
∴∠ADB=90°,BD=BC=x,
∴AD==x,
∵点E是△ABC的外接圆的圆心,
∴∠EBD=30°,
∴AE=BE=2ED,
∴AE=x,
∴等边三角形外接圆的半径BE等于边长AB的倍.
故答案为:.
【点评】此题考查了三角形的外接圆的性质以及等边三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
13.【解析】首先由△A ( http: / / www.21cnjy.com )BC的外心即是三角形三边垂直平分线的交点,所以在平面直角坐标系中作AB与BC的垂线,两垂线的交点即为△ABC的外心.
解:∵△ABC的外心即是三角形三边垂直平分线的交点,
∴作图得:
( http: / / www.21cnjy.com )
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
【点评】此题考查了三角形外心的知识.注意三角形的外心即是三角形三边垂直平分线的交点.解此题的关键是数形结合思想的应用.
14.【解析】根据题意只要举出是平行四边形但不是矩形的例子即可.
解:含有一个30°角的平行四边形的一组对边平行且相等,但不是矩形.
【点评】要说明命题不是真命题,主要能举出一个反例即可.本题答案不唯一.
15.【解析】要确定点与圆的位置关系, ( http: / / www.21cnjy.com )主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
故答案为:3<r<5.
【点评】此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.
三、解答题
16.【解析】(1)根据确定圆的条件及三角形外接圆的作法作图即可.
(2)利用反证法进行证明即可.
解:(1)如果A、B、C三点不在同一条直线上,就能确定一个圆,
作法:
①连接AB,作线段AB的垂直平分线DE;
②连接BC,作线段BC的垂直平分线FG,交DE于点O;
③以O为圆心,OB为半径作圆.⊙O就是过A、B、C三点的圆.
( http: / / www.21cnjy.com )
(2)如果A、B、C三点在同一条直线上,就不能确定一个圆,
假设过A、B、C三点可以作圆,设这个圆心为O,
由点的轨迹可知,点O在线段AB的垂直平分线l′上,
并且在线段BC的垂直平分线l″上,
即点O为′与l″的交点,
这与“过一点只有一条直线与已知直线垂直”相矛盾,
所以,过同一条直线上的三点A、B、C不能作圆.
( http: / / www.21cnjy.com )
【点评】此题比较复杂,考查的是确定圆的条件及反证法,涉及面较广,但难度适中.
17.【解析】(1)设三角形ABC中有2个或3个直角,根据三角形内角和定理即可证明;
(2)首先从结论的反面出发进而假设结论 ( http: / / www.21cnjy.com )不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,再利用勾股定理结合已知得出矛盾,进而得出答案.
证明:(1)设三角形ABC中有2个 ( http: / / www.21cnjy.com )或3个直角,则三角形的三个内角的和一定大于180°,则与三角形的三个内角的和是180度相矛盾,则△ABC中至多只能有一个是直角;
(2)假设结论不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,
设圆心为O,弦AB≠弦CD,
设AB中点为M,CD中点为N,
则OM⊥AB,ON⊥CD,且OM=ON,
根据弦长性质,AM=AB,CN=CD,
由勾股定理可知:OA2=AM2+OM2=AB2+OM2,
OC2=CN2+ON2=CD2+ON2
∵OA=OC=半径,
∴AB2+OM2=CD2+ON2
又∵OM=ON,则AB2=CD2,
即AB=CD,与假设AB≠CD矛盾,假设不成立,
故在同一个圆中,如果两条弦不等,它们的弦心距不等.
( http: / / www.21cnjy.com )
【点评】本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
18.【解析】首先作出AB的垂直平分线,再分别利用A,B为圆心,r长为半径,画弧得出交点,进而得出圆心位置,即可得出答案.
解:如图所示:⊙O即为所求.
( http: / / www.21cnjy.com )
【点评】此题主要考查了复杂作图,根据已知得出O点位置是解题关键.
二、知识回顾 1.(1)在一个平面内,线段OA绕它的一个端点O旋转一周,则另一个端点A所形成的封闭曲线叫做 圆 ;(2)圆心为O,半径为r的圆可以看成是所有到定点O的距离等于 r 的点组成的图形.(3)圆上所有的点到圆心的距离都等于 半径 .2.请你画图并想一想:当点分别在圆外和圆内时,点到圆心的距离与半径的关系分别怎样呢?经过画图可知,圆外的点到圆心的距离 大于 半径,圆内的点到圆心的距离 小于 半径.
三、新知讲解 1.点和圆的位置关系设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外 d>r ;②点P在圆上 d=r ;③点P在 圆内 d<r.点和圆的位置关系与圆心到点的距离d与半径r的关系用表格表示如下: ( http: / / www.21cnjy.com )2.作圆①过一点可作 无数 个圆;②过两点可作 无数 个圆;③过不在同一条直线上的三点可确定 一个 圆;④过 在同一条直线上的 三点不能作圆.3.三角形的外接圆经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的 外接圆 .外接圆的圆心是 三角形三条边的垂直平分线 的交点,叫做这个三角形的 外心 .4.三角形外心的位置 ( http: / / www.21cnjy.com )归纳:锐角三角形的外心在 三角形内 ;直角三角形的外心在 三角形上(斜边中点) ;钝角三角形的外心在 三角形外 .5.外接圆与内接三角形一个三角形 有且仅有 一个外接圆.一个圆有 无数 个内接三角形.
四、典例探究 扫一扫,有惊喜哦!1.判断点和圆的位置关系【例1】(2015 奉贤区一模)在直角坐标平面中,M(2,0),圆M的半径为4,那么点P(﹣2,3)与圆M的位置关系是( )A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定总结:要判断平面上一点与圆的位置关系,只需比较该点到圆心的距离d与半径r的大小关系,必要时通过画图来判断更直观.练1.如图,Rt△ABC的两条直角边BC ( http: / / www.21cnjy.com )=15cm,AC=20cm,斜边AB上的高为CD.若以C为圆心,分别以r1=11cm,r2=12cm,r3=13cm为半径作圆,试判断D点与这三个圆的位置关系. ( http: / / www.21cnjy.com )2.利用点和圆的位置关系求半径【例2】(2014秋 余姚市校级月考)若⊙O所在平面内一点P到⊙O上的点的最大距离为7,最小距离为3,则此圆的半径为( )A.5 B.2 C.10或4 D.5或2总结:平面内一点没有指明在圆内还是圆外时,注意分类讨论这两种情况。连接平面内一点与圆心并延长,可以找到平面内一点与圆上一点的最长距离和最短距离.练2.在Rt△ABC中,已知∠C=90°,BC=3,AC=4,以点B为圆心,3为半径作圆B,则:(1)AB与AC的中点D,E与圆B有怎样的位置关系?(2)若要让点A和点C有且只有一个点在圆B内,则圆B的半径应满足什么条件?3.求特殊三角形外接圆的半径【例3】若直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .总结:特殊三角形的外接圆半径求解有规律:(1)直角三角形外接圆的直径等于斜边长;(2)边长为的等边三角形外接圆的半径等于;(3)求等腰三角形外接圆的半径,先作底边的高,构造直角三角形,结合勾股定理、垂径定理求解.练3.若顶角为120°的等腰三角形的腰长为5cm,则它的外接圆的直径为 .4.用反证法证明【例4】用反证法证明:一个圆只有一个圆心.总结:反证法的步骤是:假设结论不成立;从假设出发推出矛盾;假设不成立,则结论成立.练4.用反证法证明:圆内不是直径的两条弦不能互相平分.
五、课后小测 一、选择题1.(2011秋 市中区校级期末)确定一个圆的条件是( )A.两个点确定一个圆 B.三个点确定一个圆C.四个点确定一个圆 D.不共线的三个点确定一个圆2.(2013秋 雁塔区校级月考)下列条件中,能确定圆的是( )A.以已知点O为圆心 B.以1cm长为半径C.经过已知点A,且半径为2cm D.以点O为圆心,1cm为半径3.(2014 奉贤区一模)关于半径为5的圆,下列说法正确的是( )A.若有一点到圆心的距离为5,则该点在圆外B.若有一点在圆外,则该点到圆心的距离不小于5C.圆上任意两点之间的线段长度不大于10D.圆上任意两点之间的部分可以大于10π4.(2011秋 京口区校级期末)三角形外接圆的圆心为( )A.三条高的交点 B.三条角平分线的交点C.三条垂直平分线的交点 D.三条中线的交点5.(2010秋 崂山区校级期中)有一个三角形的外接圆的圆心在它的某一边上,则这个三角形一定是( )A.等边三角形 B.直角三角形 C.锐角三角形 D.钝角三角形6.(2014秋 瓯海区校级期中)一个三角形的外接圆的圆心在这个三角形的外部,则该三角形一定是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形7.下列说法中,正确的是( )A.三点确定一个圆B.三角形的外心到三角形三边的距离相等C.三角形有且只有一个外接圆D.圆有且只有一个内接三角形8.(2013 北仑区二模)用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设( )A.有一个锐角小于45° B.每一个锐角都小于45°C.有一个锐角大于45° D.每一个锐角都大于45°9.(2015 巴中模拟)已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,,那么点P与⊙O的位置关系是( )A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定1..(2015 黄石校级模拟)一个点到圆的最小距离为3cm,最大距离为8cm,则该圆的半径是( )A.5cm或11cm B.2.5cm C.5.5cm D.2.5cm或5.5cm二、填空题11.(2014秋 郧县期中)已知矩形AB ( http: / / www.21cnjy.com )CD中,AB=6cm,AD=8cm,以A为圆心作⊙A,使B,C,D三点中,至少有一个点在圆内,且至少有一个点在圆外,则⊙A的半径r(cm)的取值范围是 .12.等边三角形的外接圆的半径等于边长的 倍.13.(2011 烟台)如图,△ABC的外心坐标是 . ( http: / / www.21cnjy.com )14.要证明“一组对边平行且相等的四边形是矩形”是假命题,可举反例 .15.(2015 盐城)如图,在矩形ABC ( http: / / www.21cnjy.com )D中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 . ( http: / / www.21cnjy.com )三、解答题16.(1999 辽宁)过A,B,C三点,能否确定一个圆?如果能,请作出圆,并写出作法;如果不能,请用反证法加以证明.17.用反证法证明:(1)△ABC中至多只能有一个角是直角;(2)在同一个圆中,如果两条弦不等,那么它们的弦心距也不等.18.(2013 青岛校级一模)如图,已知A、B两点和线段r.求作:⊙O,使其半径为r,且经过A、B两点.(任作一个即可)结论:
典例探究答案:
【例1】【解析】求得线段MP的长后与圆M的半径比较即可确定正确的选项.
解:∵M(2,0),P(﹣2,3),
∴MP==5,
∵圆M的半径为4,
∴点P在圆外,
故选:C.
【点评】考查了点与圆的位置关系,判断点与圆的位置关系,也就是比较点与圆心的距离和半径的大小关系.
练1.【解析】先根据勾股定理计算出AB=25cm,再利用面积法计算出CD=12cm,然后根据点与圆的位置关系进行判断.
解:∵Rt△ABC的两条直角边BC=15cm,AC=20cm,
∴AB==25cm,
∵BC AC=CD AB,
∴CD==12(cm),
∵所以当以r1=11cm作圆,D点在这个圆的外部;当以r2=12作圆,D点在这个圆上;当以r3=13作圆,D点在这个圆的内部.
【点评】本题考查了点与圆的 ( http: / / www.21cnjy.com )位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r.
【例2】【解析】由于点P与⊙O的位置关系不能确定,故应分两种情况进行讨论.
解:设⊙O的半径为r,
当点P在圆外时,r==2;
当点P在⊙O内时,r==5.
( http: / / www.21cnjy.com )
综上可知此圆的半径为5或2.
故选:D.
【点评】本题考查的是点与圆的位置关系,解答此题时要进行分类讨论,不要漏解.
练2.【考点】点与圆的位置关系.
【解析】(1)先利用勾股定理计算出AB=5,则得到BD=2.5,易得BE>3,然后根据点与圆的位置关系判断D,E与圆B的位置关系;
(2)由于BC=3,BA=5,根据点与圆的位置关系即可确定圆B的半径的范围.
解:(1)如图,
∵∠C=90°,BC=3,AC=4,
∴AB==5,
∵D为AB的中点,
∴BD=2.5,
∴点D在圆B内,
∵BE>BC,即BE>3,
∴点D在圆B外;
(2)设圆B的半径为r,
当3<r<5时,点A和点C有且只有一个点在圆B内.
( http: / / www.21cnjy.com )
【点评】本题考查了点与圆的位置关系:设 ( http: / / www.21cnjy.com )⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r.
【例3】【解析】直角三角形的外接圆 ( http: / / www.21cnjy.com )圆心是斜边的中点,那么半径为斜边的一半,分两种情况:①16为斜边长;②16和12为两条直角边长,由勾股定理易求得此直角三角形的斜边长,进而可求得外接圆的半径.
解:由勾股定理可知:
①当直角三角形的斜边长为16时,这个三角形的外接圆半径为8;
②当两条直角边长分别为16和12,则直角三角形的斜边长==20,
因此这个三角形的外接圆半径为10.
综上所述:这个三角形的外接圆半径等于8或10.
故答案为:10或8.
【点评】本题考查的是直角三角形的外接圆半径,重点在于理解直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的圆.
练3.【解析】作辅助线:连接AO交BC于点D、连接OB,构建等边三角形BAO,然后根据等边三角形及圆的半径与直径的关系解答.
解:连接AO交BC于点D、连接OB.
( http: / / www.21cnjy.com )
∵点O是等腰三角形ABC的外接圆圆心,
∴OA⊥BC,AD是边BC的中垂线,
∴AO是∠BAC的角平分线;
又∠BAC=120°,
∴∠BAO=60°;
又OA=OB(圆的半径),
∴∠BAO=∠OBA=60°(等边对等角),
∴∠BOA=60°(三角形的内角和定理),
∴AB=OA=OB;
又AB=5,
∴⊙O的直径是2OA=10cm.
故答案是:10cm.
【点评】本题主要考查了垂径定理、等边三角形的性质.解此类题目要注意将圆的问题转化成三角形的问题再进行计算.
【例4】【解析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此得出假设与已知定理矛盾,进而得出答案.
证明:假设⊙O有两个圆心O及O′,在圆内任作一弦AB,设弦AB的中点为P,
连结OP,O′P,则OP⊥AB,O′P⊥AB,过直线AB上一点P,同时有两条直线OP,O′P都垂直于AB,与垂线的性质矛盾,
故一个圆只有一个圆心.
( http: / / www.21cnjy.com )
【点评】此题主要考查了反证法,解此题关键要懂得反证法的意义及步骤.
练4.【解析】首先假设圆内不是直径的两条弦AC和BD互相平分于P,进而利用平行四边形的性质以及圆内接四边形的性质得出矛盾,从而得出结论.
证明:假设圆内不是直径的两条弦AC和BD互相平分于P,
∵四边形ABCD的对角线互相平分于P,
∴四边形ABCD是平行四边形,
又∵四边形ABCD是圆内接四边形,
则∠DAB与∠BCD互补,
则∠DAB与∠BCD都是直角(平行四边形对角相等),AC是直径,与假设矛盾,
所以原命题正确.
( http: / / www.21cnjy.com )
【点评】此题主要考查了反证法,正确掌握反证法的一般步骤是解题关键.
课后小测答案:
一、选择题
1.【解析】根据不在同一直线上的三个点确定一个圆判断进而得出答案即可.
解:根据不在同一直线上的三个点确定一个圆,故选项D正确.
故选:D.
【点评】此题主要考查了确定圆的条件,根据不在一条直线上的三点确定一个圆得出是解题关键.
2.【解析】确定一个圆有两个重要因素,一是圆心,而是半径,据此可以得到答案.
解:∵圆心确定,半径确定后才可以确定圆,
∴D选项正确,
故选D
【点评】本题考查了确定圆的条件,确定圆要首先确定圆的圆心,然后也要确定半径.
3.【解析】根据点与圆的位置关系进而分别判断得出即可.
解:A、关于半径为5的圆,有一点到圆心的距离为5,则该点在圆上,故此选项错误;
B、关于半径为5的圆,若有一点在圆外,则该点到圆心的距离大于5,故此选项错误;
C、圆上任意两点之间的线段长度不大于10,此选项正确;
D、圆上任意两点之间的部分不可以大于10π,故此选项错误;
故选:C.
【点评】此题主要考查了点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
①点P在圆外 d>r,②点P在圆上 d=r,③点P在圆内 d<r.
4.【解析】根据三角形外心的性质进行判断.
解:A、三角形三条高的交点是三角形的垂心,故A错误;
B、三角形三条角平分线的交点是三角形的内心,故B错误;
C、由于三角形的外心是三角形三条边的垂直平分线的交点,故C正确;
D、三角形三边中线的交点是三角形的重心,故D错误;
故选:C.
【点评】此题主要考查了三角形外心的性质.注意三角形重心、垂心、内心、外心的区别.
5.【解析】根据三角形的外接圆的圆心在它的某一边上,而这一点到三顶点距离相等,可以判断它的所在位置.
解:三角形的外接圆的圆心到三顶点距离相等,这样的点在三角形边上,
只有这个三角形是直角三角形,并且在斜边上,这样的图形只有直角三角形才符合.
故选:B.
【点评】此题主要考查了三角形的外心与三角形的位置关系只有三种,外接圆的圆心在它的某一边上,只是特殊的直角三角形具备.
6.【解析】根据三角形的外接圆的画 ( http: / / www.21cnjy.com )法得出锐角三角形的外心在三角形的内部,直角三角形的外心在直角三角形斜边的中点上,钝角三角形的外心在三角形的外部,根据以上内容得出即可.
解:∵锐角三角形的外心在三角形的内部,直角三角形的外心在直角三角形斜边的中点上,钝角三角形的外心在三角形的外部,
∴如果一个三角形的外接圆的圆心在这个三角形的外部,则该三角形一定是钝角三角形.
故选:C.
【点评】本题考查了对三角形的外接圆和外心的应用,主要考查学生的理解能力,题目比较好,难度不是很大.
7.【解析】此题应逐项分析,更要牢记“不在同一直线上的三个点确定一个圆”,本题可解.
解:A、正确的是不在同一直线上的三个点确定一个圆,故错误;
B、三角形的外心是边的垂直平分线的交点,因而外心到三个顶点的距离相等,故错误;
C、不在同一直线上的三个点确定一个圆,故正确;
D、圆有无数个内接三角形,故错误.
故选:C.
【点评】正确记忆理解定理是解决本题的关键.
8.【解析】用反证法证明命题的真假,应先按符合题设的条件,假设题设成立,再判断得出的结论是否成立即可.
解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设每一个锐角都大于45°.
故选:D.
【点评】正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理,会运用反证法证明命题的真假.
9.【解析】根据题意可知点P可能在圆外也可能在圆上,也可能在圆内,所以无法确定.
解:∵PA=,⊙O的直径为2
∴点P的位置有三种情况:①在圆外,②在圆上,③在圆内.
故选:D.
【点评】本题考查了圆的认识,做题时注意多种情况的考虑.
10.【解析】点P应分为位于圆的内部位于外部 ( http: / / www.21cnjy.com )两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
解:当点P在圆内时,最近点的距离为3cm,最远点的距离为8cm,则直径是11cm,因而半径是5.5cm;
当点P在圆外时,最近点的距离为3cm,最远点的距离为8m,则直径是5cm,因而半径是2.5cm.
故选:D.
【点评】本题考查了点与圆的位置关系,注意分两种情况进行讨论是解决本题的关键.
二、填空题
11.【解析】要确定点与圆 ( http: / / www.21cnjy.com )的位置关系,主要确定点与圆心的距离与半径的大小关系,本题可由勾股定理等性质算出点与圆心的距离d.则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解:如图:
( http: / / www.21cnjy.com )
在矩形ABCD中AC=AB,==10.
由图可知圆A的半径r的取值范围应大于AD的长,小于对角线AC的长,即6<r<10.
故答案为:6<r<10.
【点评】本题的实质是考查点与圆的位置关系,需要同学们树立数形结合的思想.
12.【解析】等边三角形外接圆的圆心是三条边垂直平分线的交点,根据等边三角形三线合一的性质,同一顶点角平分线与高重合;易得高是边长的倍,继而可得外接圆的半径是角平分线的,所以等边三角形外接圆的半径等于边长的倍.
解:如图,∵△ABC是等边三角形,
( http: / / www.21cnjy.com )
∴设AB=BC=2x,
∵AD⊥BC,
∴∠ADB=90°,BD=BC=x,
∴AD==x,
∵点E是△ABC的外接圆的圆心,
∴∠EBD=30°,
∴AE=BE=2ED,
∴AE=x,
∴等边三角形外接圆的半径BE等于边长AB的倍.
故答案为:.
【点评】此题考查了三角形的外接圆的性质以及等边三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
13.【解析】首先由△A ( http: / / www.21cnjy.com )BC的外心即是三角形三边垂直平分线的交点,所以在平面直角坐标系中作AB与BC的垂线,两垂线的交点即为△ABC的外心.
解:∵△ABC的外心即是三角形三边垂直平分线的交点,
∴作图得:
( http: / / www.21cnjy.com )
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
【点评】此题考查了三角形外心的知识.注意三角形的外心即是三角形三边垂直平分线的交点.解此题的关键是数形结合思想的应用.
14.【解析】根据题意只要举出是平行四边形但不是矩形的例子即可.
解:含有一个30°角的平行四边形的一组对边平行且相等,但不是矩形.
【点评】要说明命题不是真命题,主要能举出一个反例即可.本题答案不唯一.
15.【解析】要确定点与圆的位置关系, ( http: / / www.21cnjy.com )主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
故答案为:3<r<5.
【点评】此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.
三、解答题
16.【解析】(1)根据确定圆的条件及三角形外接圆的作法作图即可.
(2)利用反证法进行证明即可.
解:(1)如果A、B、C三点不在同一条直线上,就能确定一个圆,
作法:
①连接AB,作线段AB的垂直平分线DE;
②连接BC,作线段BC的垂直平分线FG,交DE于点O;
③以O为圆心,OB为半径作圆.⊙O就是过A、B、C三点的圆.
( http: / / www.21cnjy.com )
(2)如果A、B、C三点在同一条直线上,就不能确定一个圆,
假设过A、B、C三点可以作圆,设这个圆心为O,
由点的轨迹可知,点O在线段AB的垂直平分线l′上,
并且在线段BC的垂直平分线l″上,
即点O为′与l″的交点,
这与“过一点只有一条直线与已知直线垂直”相矛盾,
所以,过同一条直线上的三点A、B、C不能作圆.
( http: / / www.21cnjy.com )
【点评】此题比较复杂,考查的是确定圆的条件及反证法,涉及面较广,但难度适中.
17.【解析】(1)设三角形ABC中有2个或3个直角,根据三角形内角和定理即可证明;
(2)首先从结论的反面出发进而假设结论 ( http: / / www.21cnjy.com )不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,再利用勾股定理结合已知得出矛盾,进而得出答案.
证明:(1)设三角形ABC中有2个 ( http: / / www.21cnjy.com )或3个直角,则三角形的三个内角的和一定大于180°,则与三角形的三个内角的和是180度相矛盾,则△ABC中至多只能有一个是直角;
(2)假设结论不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,
设圆心为O,弦AB≠弦CD,
设AB中点为M,CD中点为N,
则OM⊥AB,ON⊥CD,且OM=ON,
根据弦长性质,AM=AB,CN=CD,
由勾股定理可知:OA2=AM2+OM2=AB2+OM2,
OC2=CN2+ON2=CD2+ON2
∵OA=OC=半径,
∴AB2+OM2=CD2+ON2
又∵OM=ON,则AB2=CD2,
即AB=CD,与假设AB≠CD矛盾,假设不成立,
故在同一个圆中,如果两条弦不等,它们的弦心距不等.
( http: / / www.21cnjy.com )
【点评】本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
18.【解析】首先作出AB的垂直平分线,再分别利用A,B为圆心,r长为半径,画弧得出交点,进而得出圆心位置,即可得出答案.
解:如图所示:⊙O即为所求.
( http: / / www.21cnjy.com )
【点评】此题主要考查了复杂作图,根据已知得出O点位置是解题关键.
同课章节目录
