【多媒体导学案】人教版数学九年级上册第24章第8课时《直线和圆的位置关系》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第8课时《直线和圆的位置关系》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 173.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 00:00:00 | ||
图片预览




文档简介
一、学习目标 探索并了解直线和圆的三种位置关系;根据圆心到直线的距离与圆的半径之间的数量关系揭示直线和圆的位置关系;能够利用公共点个数和数量关系来判断直线和圆的位置关系.
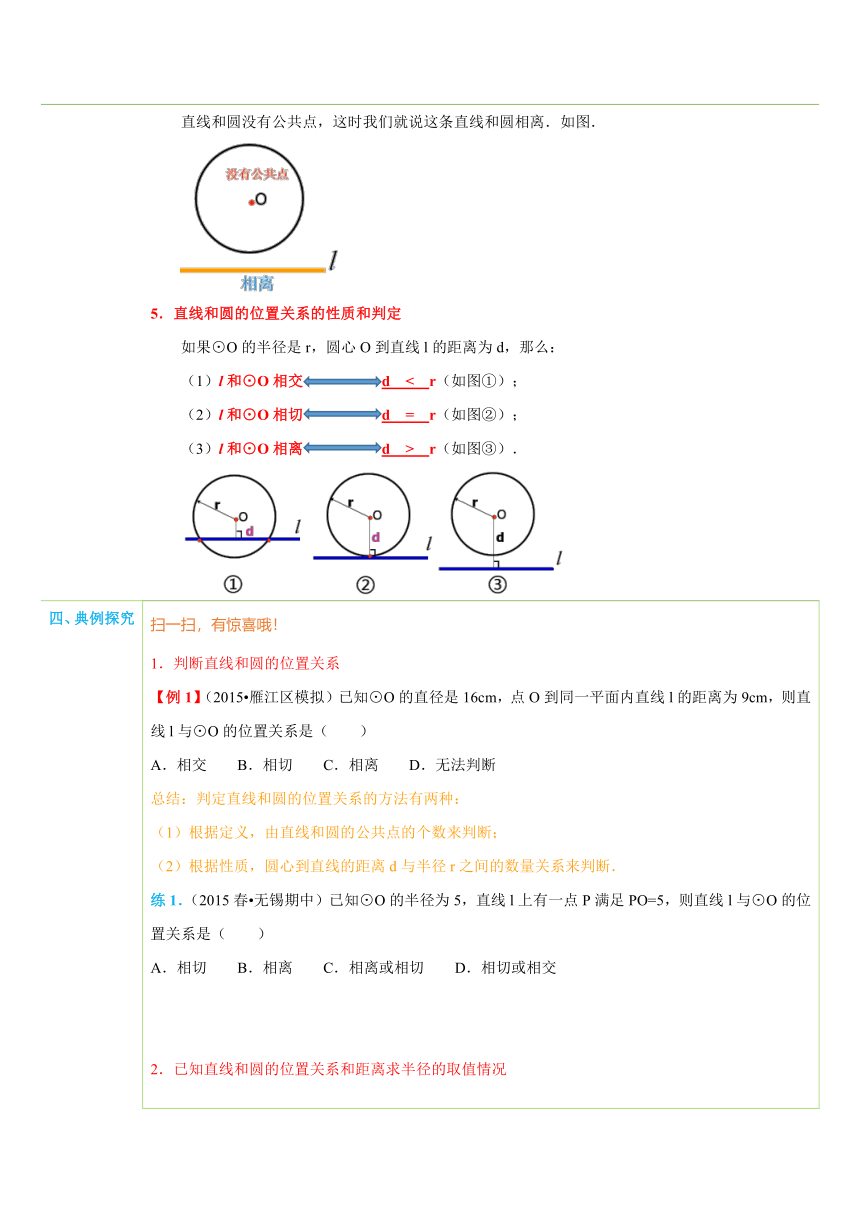
二、知识回顾 点和圆的位置关系有哪几种情况? 点在圆外;点在圆上;点在圆内 .如果点和圆心的距离为d,圆的半径为r,那么如何判定点和圆的位置关系?d>r 点在圆外 ;d=r 点在圆上 ;d三、新知讲解 1.直线和圆的位置关系直线和圆有三种位置关系:相交、相切、相离.2.直线和圆相交直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.如图. ( http: / / www.21cnjy.com )3.直线和圆相切直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.如图. ( http: / / www.21cnjy.com )4.直线和圆相离直线和圆没有公共点,这时我们就说这条直线和圆相离.如图. ( http: / / www.21cnjy.com )5.直线和圆的位置关系的性质和判定如果⊙O的半径是r,圆心O到直线l的距离为d,那么:(1)l和⊙O相交d < r(如图①);(2)l和⊙O相切d = r(如图②);(3)l和⊙O相离d > r(如图③). ( http: / / www.21cnjy.com )
四、典例探究 扫一扫,有惊喜哦!1.判断直线和圆的位置关系【例1】(2015 雁江区模拟)已知⊙O的直径是16cm,点O到同一平面内直线l的距离为9cm,则直线l与⊙O的位置关系是( )A.相交 B.相切 C.相离 D.无法判断总结:判定直线和圆的位置关系的方法有两种:(1)根据定义,由直线和圆的公共点的个数来判断;(2)根据性质,圆心到直线的距离d与半径r之间的数量关系来判断.练1.(2015春 无锡期中)已知⊙O的半径为5,直线l上有一点P满足PO=5,则直线l与⊙O的位置关系是( )A.相切 B.相离 C.相离或相切 D.相切或相交2.已知直线和圆的位置关系和距离求半径的取值情况【例2】已知等边△ABC的面积为3cm2,以A为圆心的圆与BC所在的直线l:(1)没有公共点,(2)有一个公共点,(3)有两个公共点,求三种情况下⊙A的半径的取值范围.总结: 1.直线和圆的位置关系与圆心到直线的距离和半径之间的数量关系是互相对应的,知道数量关系可以确定位置关系,知道位置关系可以确定数量关系.2.用直线和圆的位置关系来判断r的取值情况时,最好先画出图形.练2.(2011秋 丹徒区期末)已知点A ( http: / / www.21cnjy.com )的坐标是(4,﹣2),以A为圆心作圆.若⊙A上有且只有两点到x轴的距离为1,则⊙A的半径r的取值范围是 .3.利用相切判断是否受影响的实际问题【例3】如图,据气象卫星显示,一股台风10 ( http: / / www.21cnjy.com )h后将在距A城正东方向400km的B城登陆,并以每小时30km的速度向北偏西60°的BN方向移动,台风中心300km内的范围会受到台风的影响.试问:A城是否会受到这次台风的影响?如果受影响,那么A城受台风影响的时间将有多长(结果保留整数)?如果不受影响,请说明理由. ( http: / / www.21cnjy.com )总结:解决实际问题时,要注意把实际问题转化为数学问题.对于判断是否受影响的题目,关键是要计算出A城和台风运动路线的最短距离,然后用最短距离与台风影响半径作比较.判断受影响时间长短,可以先以A城为圆心,台 ( http: / / www.21cnjy.com )风与A城的安全距离(300km)为半径画圆,与台风运动路线相交,可以计算出A城受影响的路程,再用路程除以台风速度求出受影响时间.练3.2006年6月某工厂 ( http: / / www.21cnjy.com )将地处A,B两地的两个小工厂合成一个大厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修一条笔直的公路(即图中的线段AB),经测量,在A地的北偏东60°方向,B地的西偏北45°方向的C处有一半径为0.7km的公园,则修筑的这条公路会不会穿过公园?为什么?
五、课后小测 一、选择题1.(2015 黄岛区校级模拟)⊙O的半径为7cm,圆心O到直线l的距离为8cm,则直线l与⊙O的位置关系是( )A.相交 B.内含 C.相切 D.相离2.(2013 湖州模拟)在巴金的海上 ( http: / / www.21cnjy.com )日记中,有这样一段描写“果然过了一会儿,在那个地方出现了太阳的小半边脸,红是真红,却没有亮光.”这段文字中,给我们呈现是直线与圆的哪一种位置关系( )A.相交 B.相切 C.相离 D.外切3.(2015 河北模拟)已知直线l与半径为2的⊙O的位置关系是相离,则点O到直线l的距离的取值范围在数轴上的表示正确的是( )A. B. C. D.4.(2014 武汉模拟)圆的直径为13cm,如果圆心与直线的距离是d,则( )A.当d=8 cm,时,直线与圆相交B.当d=4.5 cm时,直线与圆相离C.当d=6.5 cm时,直线与圆相切D.当d=13 cm时,直线与圆相切5.(2014 广东模拟)已知⊙O与直线AB相交,且圆心O到直线AB的距离是方程2x﹣1=4的根,则⊙O的半径可为( )A.1 B.2 C.2.5 D.36.(2015 齐齐哈尔)如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( ) ( http: / / www.21cnjy.com )A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤57.(2006 常德)如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣x+与⊙O的位置关系是( ) ( http: / / www.21cnjy.com )A.相离 B.相交 C.相切 D.以下三种情形都有可能二、填空题8.(2015 建宁县校级质检)已 ( http: / / www.21cnjy.com )知⊙O的半径为R,点O到直线m的距离为d,R、d是方程x2﹣4x+a=0的两根,当直线m与⊙O相切时,a= .9.(2015 杭州模拟)已知直线L与半径为4的圆0相交,则点O到直线L的距离d可取的整数值是 .10.(2015 杭州模拟)⊙O的半径为5,直线l和点O的距离为d,若直线l与⊙O有公共点,则d的范围 .11.(2015 闵行区二模)在R ( http: / / www.21cnjy.com )t△ABC中,∠C=90°,AC=3,BC=4,如果以点C为圆心,r为半径的圆与直线AC相切,那么r= .12.(2011秋 惠山区校级期中)在直角坐标系中,以P(3,1)为圆心,r为半径的圆与坐标轴恰好有三个公共点,则r的值为 .三、解答题13.(2014 同安区质检)如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由. ( http: / / www.21cnjy.com )14.(2012 崇左)已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.(1)若r=12cm,试判断⊙P与OB位置关系;(2)若⊙P与OB相离,试求出r需满足的条件. ( http: / / www.21cnjy.com )15.(2014秋 丹阳市校级期中)如图,公 ( http: / / www.21cnjy.com )路MN与公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否受到噪音影响?说明理由;如果受影响,且知拖拉机的速度为18km/h,那么学校受影响的时间是多少秒?
典例探究答案:
【例1】【解析】已知圆的半 ( http: / / www.21cnjy.com )径是r,圆心到直线的距离是d,当d=r时,直线和圆相切,当d>r时,直线和圆相离,当d<r时,直线和圆相交,根据以上内容判断即可.
解:∵⊙O的直径是16cm,
∴⊙O的半径是8cm,
∵点O到同一平面内直线l的距离为9cm,
∴直线l与⊙O的位置关系是相离,
故选C.
点评:本题考查了直线和圆的位置关系的应用,理解直线和圆的位置关系的内容是解此题的关键.
练1.【解析】根据直线与 ( http: / / www.21cnjy.com )圆的位置关系来判定.判断直线和圆的位置关系:①直线l和⊙O相交 d<r;②直线l和⊙O相切 d=r;③直线l和⊙O相离 d>r.分OP垂直于直线l,OP不垂直直线l两种情况讨论.
解:当OP垂直于直线l时,即圆心O到直线l的距离d=5=r,⊙O与l相切;
当OP不垂直于直线l时,即圆心O到直线l的距离d<5=r,⊙O与直线l相交.
故直线l与⊙O的位置关系是相切或相交.
故选:D.
点评:本题考查直线与圆的位置关系.解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.
【例2】【解析】作AD⊥BC于D,如图 ( http: / / www.21cnjy.com ),根据等边三角形的性质和面积公式计算出AD,然后根据直线和圆的位置关系的判定方法确定⊙A的半径的取值范围.
解:作AD⊥BC于D,如图,
( http: / / www.21cnjy.com )
∵△ABC为等边三角形,
∴∠BAD=30°,AB=2BD,
∴AD=BD,
∵AD BC=3,
∴ BD 2BD=3,
∴BD=,
∴AD=×=3,
(1)当⊙A的半径r小于AD时,以A为圆心的圆与BC所在的直线l没有公共点,即0<r<3;
(2)当⊙A的半径r等于AD时,以A为圆心的圆与BC所在的直线l有一个公共点,即r=3;
(3)当⊙A的半径r大于AD时,以A为圆心的圆与BC所在的直线l有两个公共点,即r>3.
点评:本题考查了直线和圆的位置关系:设 ( http: / / www.21cnjy.com )⊙O的半径为r,圆心O到直线l的距离为d,直线l和⊙O相交 d<r;直线l和⊙O相切 d=r;直线l和⊙O相离 d>r.也考查了等边三角形的性质.
练2.【解析】由点A的纵坐标为﹣2 ( http: / / www.21cnjy.com ),可知点A到x轴的距离为2,以点A为圆心的圆上只有两点到直线l的距离为1,则两个交点在到直线l的距离是1的直线m上,圆与直线m的位置关系是相交,据此即可判断.
解:∵点A的坐标是(4,﹣2),
∴点A到x轴的距离为2,
∴以点A为圆心的圆上只有两点到直线l的距离为1,则两个交点在到直线l的距离是1的直线m上.
则直线m到圆心O的距离是:1+2=3或2﹣1=1.
圆O与直线m相交,因而该圆的半径r的取值范围是1<r<3.
故答案是:1<r<3.
点评:本题主要考查了直线与圆的位置关系以及到定直线的距离等于定长的点的几何,根据已知条件确定直线与圆相交是解题的关键.
【例3】【解析】(1)是否会受到影响,需 ( http: / / www.21cnjy.com )要求得点A到台风所走路线的最短距离,根据垂线段最短,即作AC⊥BN于C,再根据直角三角形的性质进行计算比较;
(2)需要计算出受影响的总路程,再根据时间=路程÷速度进行计算.
解:(1)过A作AC⊥BN于C,
( http: / / www.21cnjy.com )
则∠ABC=90°﹣60°=30°,∠ACB=90°,AB=400km,
则AC=AB=200<300,
∴A市会受到台风影响;
(2)过A作AD=AE=300km,交BN于点D,E,
( http: / / www.21cnjy.com )
∴DC===100km,
∵DC=CE,A市气象站测得台风中心在A市正东方向400km的B处,以30km/时的速度向北偏西60°的BN方向移动,
∴该市受台风影响的时间为:2×100÷30=小时≈12小时,
即A城是会受到这次台风的影响,A城受台风影响的时间约12小时.
点评:此类是否受影响的题目,必须计算出最短距离进行分析,注意垂线段最短的性质;题目比较好,难度适中.
练3.【解析】要判断是否穿过公园,只需求得点C到AB的垂线段的长度,然后和半径进行比较即可.
解:如右图所示,过点C作CD⊥AB,垂足为D.
( http: / / www.21cnjy.com )
∵∠B=45°,
∴∠BCD=45°,CD=BD.
设CD=x,则BD=x;
由∠A=30°知AC=2x,AD==x,
∴x+x=2,
(+1)x=2,
则x===﹣1;
即CD=﹣1≈0.732(km)>0.7km.
也就是说,以C为圆心,以0.7km为半径的圆与AB相离.
答:计划修筑的这条公路不会穿过公园.
点评:能够根据特殊角发现边之间的关系型,求得点C到直线的最短距离,然后和半径进行比较即可.
课后小测答案:
一、选择题
1.【解析】解:∵⊙O的半径为7cm,圆心O到直线l的距离为8cm,7<8,
∴直线l与⊙O相离.
故选D.
2.【解析】解:根据在那个地方出现了太阳的小半边脸,可知直线和圆此时是相交的位置关系.
故选A.
3.【解析】解:∵l与半径为2的⊙O的位置关系是相离,
∴点O到直线l的距离的取值范围d>2.
故选A.
4.【解析】解:已知圆的直径为13cm,则半径为6.5cm,
当d=6.5cm时,直线与圆相切,d<6.5cm直线与圆相交,d>6.5cm直线与圆相离,
故A、B、D错误,C正确,
故选C.
5.【解析】解:∵圆心O到直线AB的距离是方程2x﹣1=4的根,
∴d=2.5,
∵⊙O与直线AB相交,
∴d=3,
故选D.
6.【解析】解:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴AB=2=8.
∵大圆的弦AB与小圆有公共点,即相切或相交,
∴8≤AB≤10.
故选:A.
7.【解析】解:圆心O到直线y=﹣x+的距离是1,它等于圆的半径1,则直线和圆相切.
故选C.
二、填空题
8.【解析】解:∵直线和圆相切,
∴d=r,
∴△=16﹣4a=0,
∴a=4,
故答案为:4
9.【解析】解:∵直线L与半径为4的圆0相交,
∴点O到直线L的距离d的取值范围为:0≤d<4,
∴d可取的整数值是0,1,2,3.
故答案为:0,1,2,3.
10.【解析】解:∵⊙O的半径为5,直线l和点O的距离为d,直线l与⊙O有公共点,
∴直线和圆相交或相切,
∴0≤d≤5,
故答案为:0≤d≤5.
11.【解析】解:∵∠C=90°,AC=3,BC=4,
∴AB=5,
设圆心C到AB的距离为d,
则×3×4=×5×d,
d=,
根据⊙C与AB相切,则圆心C到AB的距离就是半径的长,
r=,
故答案为:.
12.【解析】解:当圆心在(3,1)且与y轴相切时,r=3,
当圆心在(3,1)与经过原点时,r=.
故答案为:3或.
三、解答题
13.【解析】解:⊙A与直线BC相交.
( http: / / www.21cnjy.com )
过A作AD⊥BC,垂足为点D.
∵AB=AC,BC=16,
∴BD=BC=×16=8,
在Rt△ABC中,AB=10,BD=8,
∴AD===6,
∵⊙O的半径为7,
∴AD<r,
⊙A与直线BC相交.
14.【解析】解:过点P作PC⊥OB,垂足为C,则∠OCP=90°.
( http: / / www.21cnjy.com )
∵∠AOB=30°,OP=24cm,
∴PC=OP=12cm.
(1)当r=12cm时,r=PC,
∴⊙P与OB相切,
即⊙P与OB位置关系是相切.
(2)当⊙P与OB相离时,r<PC,
∴r需满足的条件是:0cm<r<12cm.
15.【解析】解:学校受到噪音影响.
理由如下:
作AH⊥MN于H,如图,
( http: / / www.21cnjy.com )
∵PA=160m,∠QPN=30°,
∴AH=PA=80m,
而80m<100m,∴拖拉机在公路MN上沿PN方向行驶时,学校受到噪音影响,
以点A为圆心,100m为半径作⊙A交MN于B、C,如图,
∵AH⊥BC,
∴BH=CH,
在Rt△ABH中,AB=100m,AH=80m,
BH= =60m,
∴BC=2BH=120m,
∵拖拉机的速度=18km/h=5m/s,
∴拖拉机在线段BC上行驶所需要的时间==24(秒),
∴学校受影响的时间为24秒.
二、知识回顾 点和圆的位置关系有哪几种情况? 点在圆外;点在圆上;点在圆内 .如果点和圆心的距离为d,圆的半径为r,那么如何判定点和圆的位置关系?d>r 点在圆外 ;d=r 点在圆上 ;d
四、典例探究 扫一扫,有惊喜哦!1.判断直线和圆的位置关系【例1】(2015 雁江区模拟)已知⊙O的直径是16cm,点O到同一平面内直线l的距离为9cm,则直线l与⊙O的位置关系是( )A.相交 B.相切 C.相离 D.无法判断总结:判定直线和圆的位置关系的方法有两种:(1)根据定义,由直线和圆的公共点的个数来判断;(2)根据性质,圆心到直线的距离d与半径r之间的数量关系来判断.练1.(2015春 无锡期中)已知⊙O的半径为5,直线l上有一点P满足PO=5,则直线l与⊙O的位置关系是( )A.相切 B.相离 C.相离或相切 D.相切或相交2.已知直线和圆的位置关系和距离求半径的取值情况【例2】已知等边△ABC的面积为3cm2,以A为圆心的圆与BC所在的直线l:(1)没有公共点,(2)有一个公共点,(3)有两个公共点,求三种情况下⊙A的半径的取值范围.总结: 1.直线和圆的位置关系与圆心到直线的距离和半径之间的数量关系是互相对应的,知道数量关系可以确定位置关系,知道位置关系可以确定数量关系.2.用直线和圆的位置关系来判断r的取值情况时,最好先画出图形.练2.(2011秋 丹徒区期末)已知点A ( http: / / www.21cnjy.com )的坐标是(4,﹣2),以A为圆心作圆.若⊙A上有且只有两点到x轴的距离为1,则⊙A的半径r的取值范围是 .3.利用相切判断是否受影响的实际问题【例3】如图,据气象卫星显示,一股台风10 ( http: / / www.21cnjy.com )h后将在距A城正东方向400km的B城登陆,并以每小时30km的速度向北偏西60°的BN方向移动,台风中心300km内的范围会受到台风的影响.试问:A城是否会受到这次台风的影响?如果受影响,那么A城受台风影响的时间将有多长(结果保留整数)?如果不受影响,请说明理由. ( http: / / www.21cnjy.com )总结:解决实际问题时,要注意把实际问题转化为数学问题.对于判断是否受影响的题目,关键是要计算出A城和台风运动路线的最短距离,然后用最短距离与台风影响半径作比较.判断受影响时间长短,可以先以A城为圆心,台 ( http: / / www.21cnjy.com )风与A城的安全距离(300km)为半径画圆,与台风运动路线相交,可以计算出A城受影响的路程,再用路程除以台风速度求出受影响时间.练3.2006年6月某工厂 ( http: / / www.21cnjy.com )将地处A,B两地的两个小工厂合成一个大厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修一条笔直的公路(即图中的线段AB),经测量,在A地的北偏东60°方向,B地的西偏北45°方向的C处有一半径为0.7km的公园,则修筑的这条公路会不会穿过公园?为什么?
五、课后小测 一、选择题1.(2015 黄岛区校级模拟)⊙O的半径为7cm,圆心O到直线l的距离为8cm,则直线l与⊙O的位置关系是( )A.相交 B.内含 C.相切 D.相离2.(2013 湖州模拟)在巴金的海上 ( http: / / www.21cnjy.com )日记中,有这样一段描写“果然过了一会儿,在那个地方出现了太阳的小半边脸,红是真红,却没有亮光.”这段文字中,给我们呈现是直线与圆的哪一种位置关系( )A.相交 B.相切 C.相离 D.外切3.(2015 河北模拟)已知直线l与半径为2的⊙O的位置关系是相离,则点O到直线l的距离的取值范围在数轴上的表示正确的是( )A. B. C. D.4.(2014 武汉模拟)圆的直径为13cm,如果圆心与直线的距离是d,则( )A.当d=8 cm,时,直线与圆相交B.当d=4.5 cm时,直线与圆相离C.当d=6.5 cm时,直线与圆相切D.当d=13 cm时,直线与圆相切5.(2014 广东模拟)已知⊙O与直线AB相交,且圆心O到直线AB的距离是方程2x﹣1=4的根,则⊙O的半径可为( )A.1 B.2 C.2.5 D.36.(2015 齐齐哈尔)如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( ) ( http: / / www.21cnjy.com )A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤57.(2006 常德)如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣x+与⊙O的位置关系是( ) ( http: / / www.21cnjy.com )A.相离 B.相交 C.相切 D.以下三种情形都有可能二、填空题8.(2015 建宁县校级质检)已 ( http: / / www.21cnjy.com )知⊙O的半径为R,点O到直线m的距离为d,R、d是方程x2﹣4x+a=0的两根,当直线m与⊙O相切时,a= .9.(2015 杭州模拟)已知直线L与半径为4的圆0相交,则点O到直线L的距离d可取的整数值是 .10.(2015 杭州模拟)⊙O的半径为5,直线l和点O的距离为d,若直线l与⊙O有公共点,则d的范围 .11.(2015 闵行区二模)在R ( http: / / www.21cnjy.com )t△ABC中,∠C=90°,AC=3,BC=4,如果以点C为圆心,r为半径的圆与直线AC相切,那么r= .12.(2011秋 惠山区校级期中)在直角坐标系中,以P(3,1)为圆心,r为半径的圆与坐标轴恰好有三个公共点,则r的值为 .三、解答题13.(2014 同安区质检)如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由. ( http: / / www.21cnjy.com )14.(2012 崇左)已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.(1)若r=12cm,试判断⊙P与OB位置关系;(2)若⊙P与OB相离,试求出r需满足的条件. ( http: / / www.21cnjy.com )15.(2014秋 丹阳市校级期中)如图,公 ( http: / / www.21cnjy.com )路MN与公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否受到噪音影响?说明理由;如果受影响,且知拖拉机的速度为18km/h,那么学校受影响的时间是多少秒?
典例探究答案:
【例1】【解析】已知圆的半 ( http: / / www.21cnjy.com )径是r,圆心到直线的距离是d,当d=r时,直线和圆相切,当d>r时,直线和圆相离,当d<r时,直线和圆相交,根据以上内容判断即可.
解:∵⊙O的直径是16cm,
∴⊙O的半径是8cm,
∵点O到同一平面内直线l的距离为9cm,
∴直线l与⊙O的位置关系是相离,
故选C.
点评:本题考查了直线和圆的位置关系的应用,理解直线和圆的位置关系的内容是解此题的关键.
练1.【解析】根据直线与 ( http: / / www.21cnjy.com )圆的位置关系来判定.判断直线和圆的位置关系:①直线l和⊙O相交 d<r;②直线l和⊙O相切 d=r;③直线l和⊙O相离 d>r.分OP垂直于直线l,OP不垂直直线l两种情况讨论.
解:当OP垂直于直线l时,即圆心O到直线l的距离d=5=r,⊙O与l相切;
当OP不垂直于直线l时,即圆心O到直线l的距离d<5=r,⊙O与直线l相交.
故直线l与⊙O的位置关系是相切或相交.
故选:D.
点评:本题考查直线与圆的位置关系.解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.
【例2】【解析】作AD⊥BC于D,如图 ( http: / / www.21cnjy.com ),根据等边三角形的性质和面积公式计算出AD,然后根据直线和圆的位置关系的判定方法确定⊙A的半径的取值范围.
解:作AD⊥BC于D,如图,
( http: / / www.21cnjy.com )
∵△ABC为等边三角形,
∴∠BAD=30°,AB=2BD,
∴AD=BD,
∵AD BC=3,
∴ BD 2BD=3,
∴BD=,
∴AD=×=3,
(1)当⊙A的半径r小于AD时,以A为圆心的圆与BC所在的直线l没有公共点,即0<r<3;
(2)当⊙A的半径r等于AD时,以A为圆心的圆与BC所在的直线l有一个公共点,即r=3;
(3)当⊙A的半径r大于AD时,以A为圆心的圆与BC所在的直线l有两个公共点,即r>3.
点评:本题考查了直线和圆的位置关系:设 ( http: / / www.21cnjy.com )⊙O的半径为r,圆心O到直线l的距离为d,直线l和⊙O相交 d<r;直线l和⊙O相切 d=r;直线l和⊙O相离 d>r.也考查了等边三角形的性质.
练2.【解析】由点A的纵坐标为﹣2 ( http: / / www.21cnjy.com ),可知点A到x轴的距离为2,以点A为圆心的圆上只有两点到直线l的距离为1,则两个交点在到直线l的距离是1的直线m上,圆与直线m的位置关系是相交,据此即可判断.
解:∵点A的坐标是(4,﹣2),
∴点A到x轴的距离为2,
∴以点A为圆心的圆上只有两点到直线l的距离为1,则两个交点在到直线l的距离是1的直线m上.
则直线m到圆心O的距离是:1+2=3或2﹣1=1.
圆O与直线m相交,因而该圆的半径r的取值范围是1<r<3.
故答案是:1<r<3.
点评:本题主要考查了直线与圆的位置关系以及到定直线的距离等于定长的点的几何,根据已知条件确定直线与圆相交是解题的关键.
【例3】【解析】(1)是否会受到影响,需 ( http: / / www.21cnjy.com )要求得点A到台风所走路线的最短距离,根据垂线段最短,即作AC⊥BN于C,再根据直角三角形的性质进行计算比较;
(2)需要计算出受影响的总路程,再根据时间=路程÷速度进行计算.
解:(1)过A作AC⊥BN于C,
( http: / / www.21cnjy.com )
则∠ABC=90°﹣60°=30°,∠ACB=90°,AB=400km,
则AC=AB=200<300,
∴A市会受到台风影响;
(2)过A作AD=AE=300km,交BN于点D,E,
( http: / / www.21cnjy.com )
∴DC===100km,
∵DC=CE,A市气象站测得台风中心在A市正东方向400km的B处,以30km/时的速度向北偏西60°的BN方向移动,
∴该市受台风影响的时间为:2×100÷30=小时≈12小时,
即A城是会受到这次台风的影响,A城受台风影响的时间约12小时.
点评:此类是否受影响的题目,必须计算出最短距离进行分析,注意垂线段最短的性质;题目比较好,难度适中.
练3.【解析】要判断是否穿过公园,只需求得点C到AB的垂线段的长度,然后和半径进行比较即可.
解:如右图所示,过点C作CD⊥AB,垂足为D.
( http: / / www.21cnjy.com )
∵∠B=45°,
∴∠BCD=45°,CD=BD.
设CD=x,则BD=x;
由∠A=30°知AC=2x,AD==x,
∴x+x=2,
(+1)x=2,
则x===﹣1;
即CD=﹣1≈0.732(km)>0.7km.
也就是说,以C为圆心,以0.7km为半径的圆与AB相离.
答:计划修筑的这条公路不会穿过公园.
点评:能够根据特殊角发现边之间的关系型,求得点C到直线的最短距离,然后和半径进行比较即可.
课后小测答案:
一、选择题
1.【解析】解:∵⊙O的半径为7cm,圆心O到直线l的距离为8cm,7<8,
∴直线l与⊙O相离.
故选D.
2.【解析】解:根据在那个地方出现了太阳的小半边脸,可知直线和圆此时是相交的位置关系.
故选A.
3.【解析】解:∵l与半径为2的⊙O的位置关系是相离,
∴点O到直线l的距离的取值范围d>2.
故选A.
4.【解析】解:已知圆的直径为13cm,则半径为6.5cm,
当d=6.5cm时,直线与圆相切,d<6.5cm直线与圆相交,d>6.5cm直线与圆相离,
故A、B、D错误,C正确,
故选C.
5.【解析】解:∵圆心O到直线AB的距离是方程2x﹣1=4的根,
∴d=2.5,
∵⊙O与直线AB相交,
∴d=3,
故选D.
6.【解析】解:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴AB=2=8.
∵大圆的弦AB与小圆有公共点,即相切或相交,
∴8≤AB≤10.
故选:A.
7.【解析】解:圆心O到直线y=﹣x+的距离是1,它等于圆的半径1,则直线和圆相切.
故选C.
二、填空题
8.【解析】解:∵直线和圆相切,
∴d=r,
∴△=16﹣4a=0,
∴a=4,
故答案为:4
9.【解析】解:∵直线L与半径为4的圆0相交,
∴点O到直线L的距离d的取值范围为:0≤d<4,
∴d可取的整数值是0,1,2,3.
故答案为:0,1,2,3.
10.【解析】解:∵⊙O的半径为5,直线l和点O的距离为d,直线l与⊙O有公共点,
∴直线和圆相交或相切,
∴0≤d≤5,
故答案为:0≤d≤5.
11.【解析】解:∵∠C=90°,AC=3,BC=4,
∴AB=5,
设圆心C到AB的距离为d,
则×3×4=×5×d,
d=,
根据⊙C与AB相切,则圆心C到AB的距离就是半径的长,
r=,
故答案为:.
12.【解析】解:当圆心在(3,1)且与y轴相切时,r=3,
当圆心在(3,1)与经过原点时,r=.
故答案为:3或.
三、解答题
13.【解析】解:⊙A与直线BC相交.
( http: / / www.21cnjy.com )
过A作AD⊥BC,垂足为点D.
∵AB=AC,BC=16,
∴BD=BC=×16=8,
在Rt△ABC中,AB=10,BD=8,
∴AD===6,
∵⊙O的半径为7,
∴AD<r,
⊙A与直线BC相交.
14.【解析】解:过点P作PC⊥OB,垂足为C,则∠OCP=90°.
( http: / / www.21cnjy.com )
∵∠AOB=30°,OP=24cm,
∴PC=OP=12cm.
(1)当r=12cm时,r=PC,
∴⊙P与OB相切,
即⊙P与OB位置关系是相切.
(2)当⊙P与OB相离时,r<PC,
∴r需满足的条件是:0cm<r<12cm.
15.【解析】解:学校受到噪音影响.
理由如下:
作AH⊥MN于H,如图,
( http: / / www.21cnjy.com )
∵PA=160m,∠QPN=30°,
∴AH=PA=80m,
而80m<100m,∴拖拉机在公路MN上沿PN方向行驶时,学校受到噪音影响,
以点A为圆心,100m为半径作⊙A交MN于B、C,如图,
∵AH⊥BC,
∴BH=CH,
在Rt△ABH中,AB=100m,AH=80m,
BH= =60m,
∴BC=2BH=120m,
∵拖拉机的速度=18km/h=5m/s,
∴拖拉机在线段BC上行驶所需要的时间==24(秒),
∴学校受影响的时间为24秒.
同课章节目录
