【多媒体导学案】人教版数学九年级上册第24章第10课时切线长定理和内切圆(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第10课时切线长定理和内切圆(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 323.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 00:00:00 | ||
图片预览

文档简介
一、学习目标 理解切线长的定义;掌握切线长定理,并能灵活运用切线长定理解题;了解三角形的内切圆、三角形的内心、圆的外切三角形的概念,会作已知三角形的内切圆;通过探究作三角形的内切圆的过程,归纳内心的性质,进一步提高归纳和作图的能力.
二、知识回顾 确定圆的条件是什么?(1)圆心与半径;(2)不在同一直线上的三点.叙述角平分线的性质与判定.性质:角平分线上的点到这个角两边的距离相等.判定:到一个角两边的距离相等的点在这个角的平分线上.和圆有唯一公共点的直线叫圆的切线;圆的切线垂直于过切点的半径.
三、新知讲解 1.切线长经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.几何语言:如图,过圆O外一点P作圆的一条切线,切点为A,则线段PA的长叫做点P到圆O的切线长. ( http: / / www.21cnjy.com )2.切线长定理从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.如图,因为PA、PB是圆O的两条切线,所以:(1)PA=PB;(2)∠APO=∠BPO=∠APB. ( http: / / www.21cnjy.com )3.三角形的内切圆与三角形各边都相切的圆叫做这个三角形的内切圆.这个三角形叫做圆的外切三角形.4.三角形的内心三角形内切圆的圆心叫做三角形的内心,三角形的内心是三角形三条角平分线的交点,这点到三边的距离相等,且必在三角形内部.
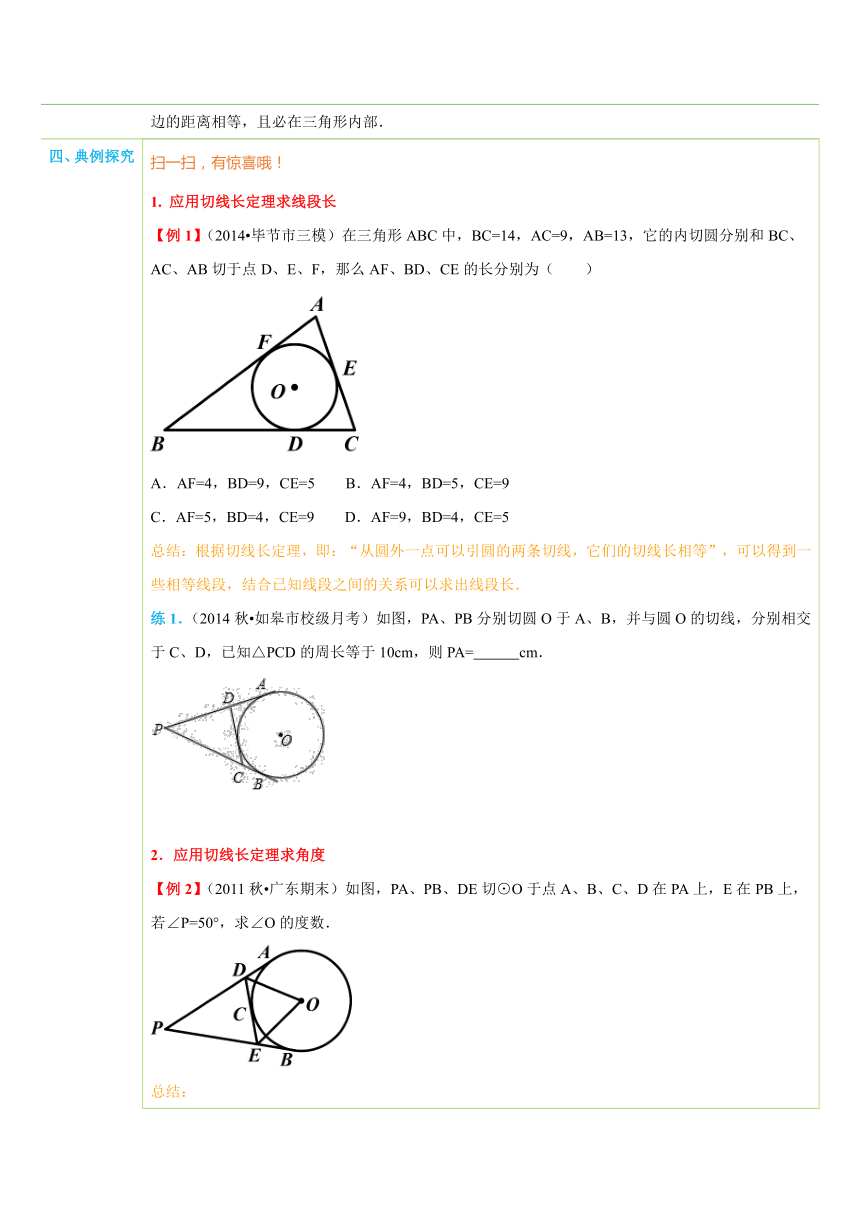
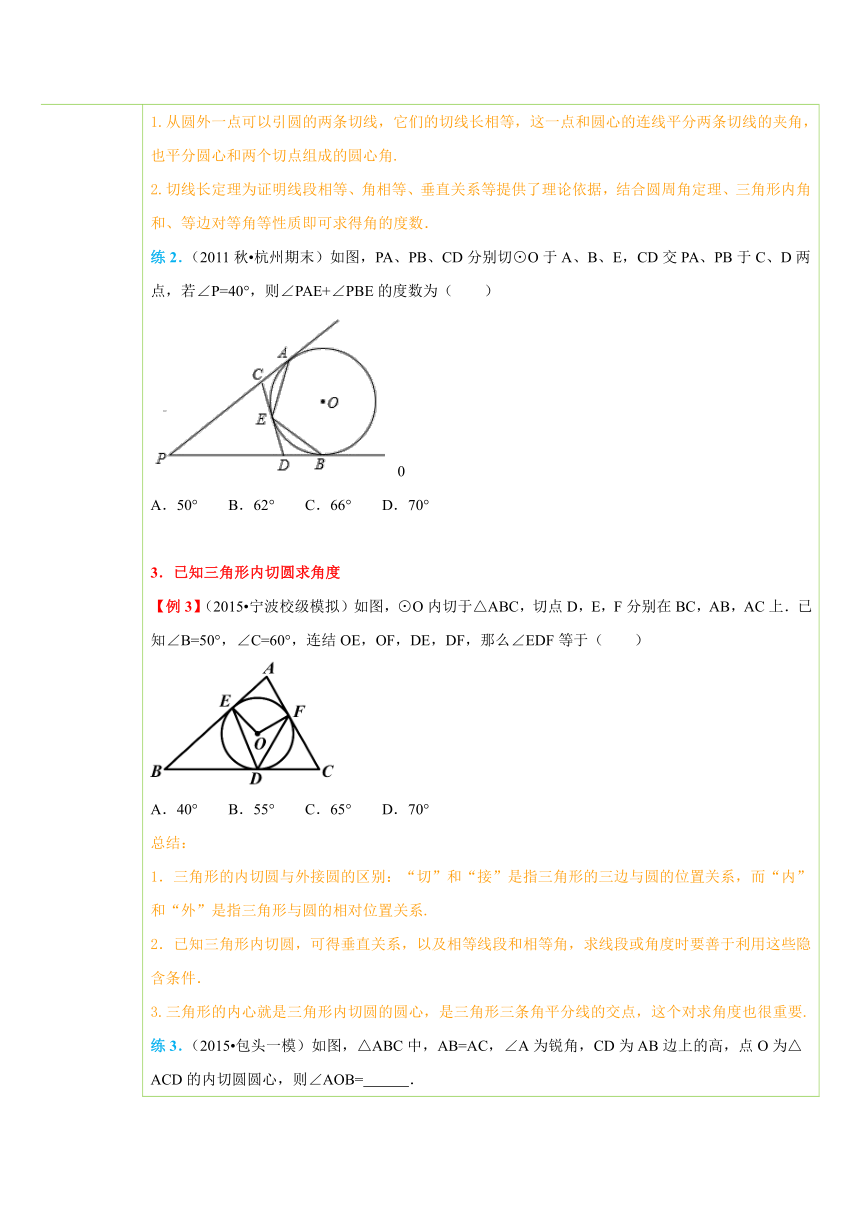
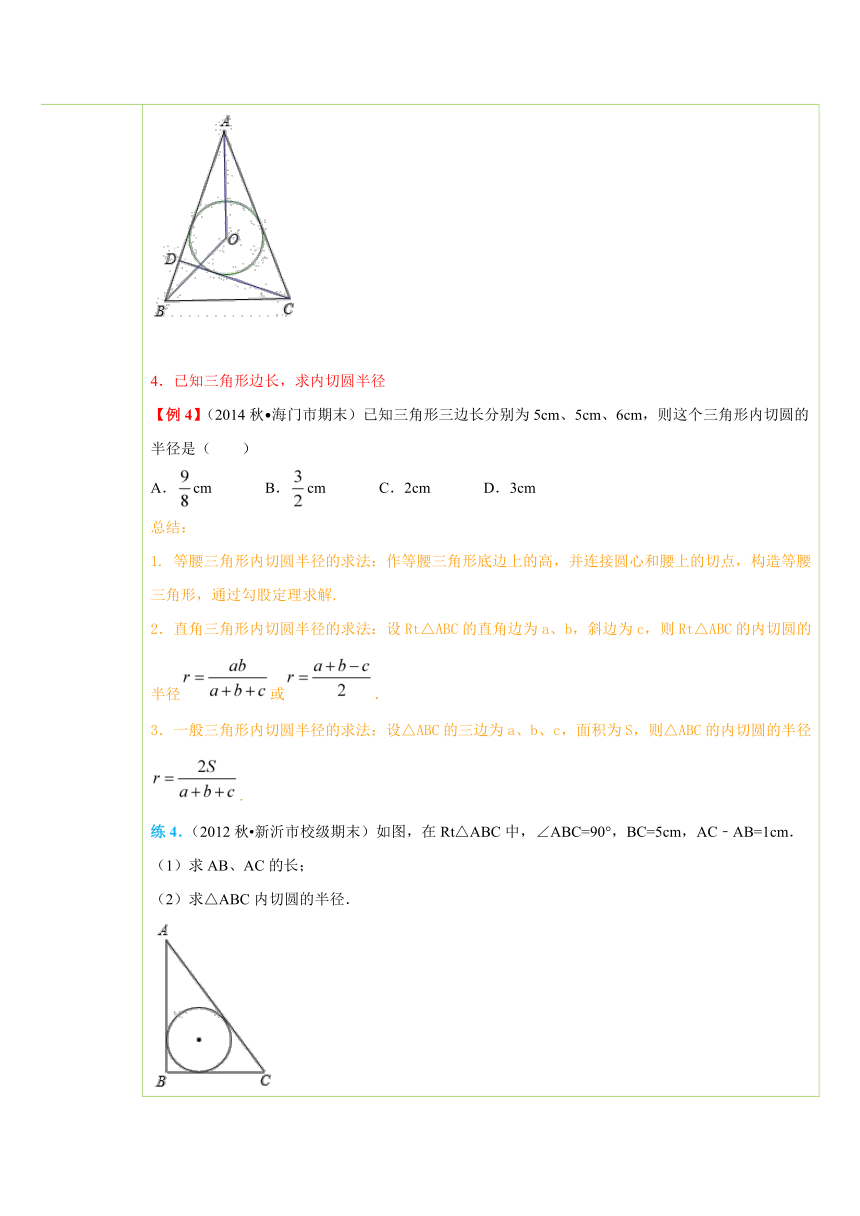
四、典例探究 扫一扫,有惊喜哦!1. 应用切线长定理求线段长【例1】(2014 毕节市三模)在三角形 ( http: / / www.21cnjy.com )ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( ) ( http: / / www.21cnjy.com )A.AF=4,BD=9,CE=5 B.AF=4,BD=5,CE=9C.AF=5,BD=4,CE=9 D.AF=9,BD=4,CE=5总结:根据切线长定理,即:“从圆外一点可以引圆的两条切线,它们的切线长相等”,可以得到一些相等线段,结合已知线段之间的关系可以求出线段长.练1.(2014秋 如皋市校级月考)如图, ( http: / / www.21cnjy.com )PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA= cm. ( http: / / www.21cnjy.com )2.应用切线长定理求角度【例2】(2011秋 广东期末)如图,PA、PB、DE切⊙O于点A、B、C、D在PA上,E在PB上,若∠P=50°,求∠O的度数. ( http: / / www.21cnjy.com )总结:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角,也平分圆心和两个切点组成的圆心角.切线长定理为证明线段相等、角相等、垂直关系等提供了理论依据,结合圆周角定理、三角形内角和、等边对等角等性质即可求得角的度数.练2.(2011秋 杭州期末)如图,PA、 ( http: / / www.21cnjy.com )PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=40°,则∠PAE+∠PBE的度数为( ) ( http: / / www.21cnjy.com )0A.50° B.62° C.66° D.70°3.已知三角形内切圆求角度【例3】(2015 宁波校 ( http: / / www.21cnjy.com )级模拟)如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( ) ( http: / / www.21cnjy.com )A.40° B.55° C.65° D.70°总结:1.三角形的内切圆与外接圆的区别:“切”和“接”是指三角形的三边与圆的位置关系,而“内”和“外”是指三角形与圆的相对位置关系.2.已知三角形内切圆,可得垂直关系,以及相等线段和相等角,求线段或角度时要善于利用这些隐含条件.3.三角形的内心就是三角形内切圆的圆心,是三角形三条角平分线的交点,这个对求角度也很重要.练3.(2015 包头一模)如图,△A ( http: / / www.21cnjy.com )BC中,AB=AC,∠A为锐角,CD为AB边上的高,点O为△ACD的内切圆圆心,则∠AOB= . ( http: / / www.21cnjy.com )4.已知三角形边长,求内切圆半径【例4】(2014秋 海门市期末)已知三角形三边长分别为5cm、5cm、6cm,则这个三角形内切圆的半径是( )A.cm B.cm C.2cm D.3cm总结:1. 等腰三角形内切圆半径的求法:作等腰三角形底边上的高,并连接圆心和腰上的切点,构造等腰三角形,通过勾股定理求解.2.直角三角形内切圆半径的求法:设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的内切圆的半径或.3.一般三角形内切圆半径的求法:设△ABC的三边为a、b、c,面积为S,则△ABC的内切圆的半径.练4.(2012秋 新沂市校级期末)如图,在Rt△ABC中,∠ABC=90°,BC=5cm,AC﹣AB=1cm.(1)求AB、AC的长;(2)求△ABC内切圆的半径. ( http: / / www.21cnjy.com )
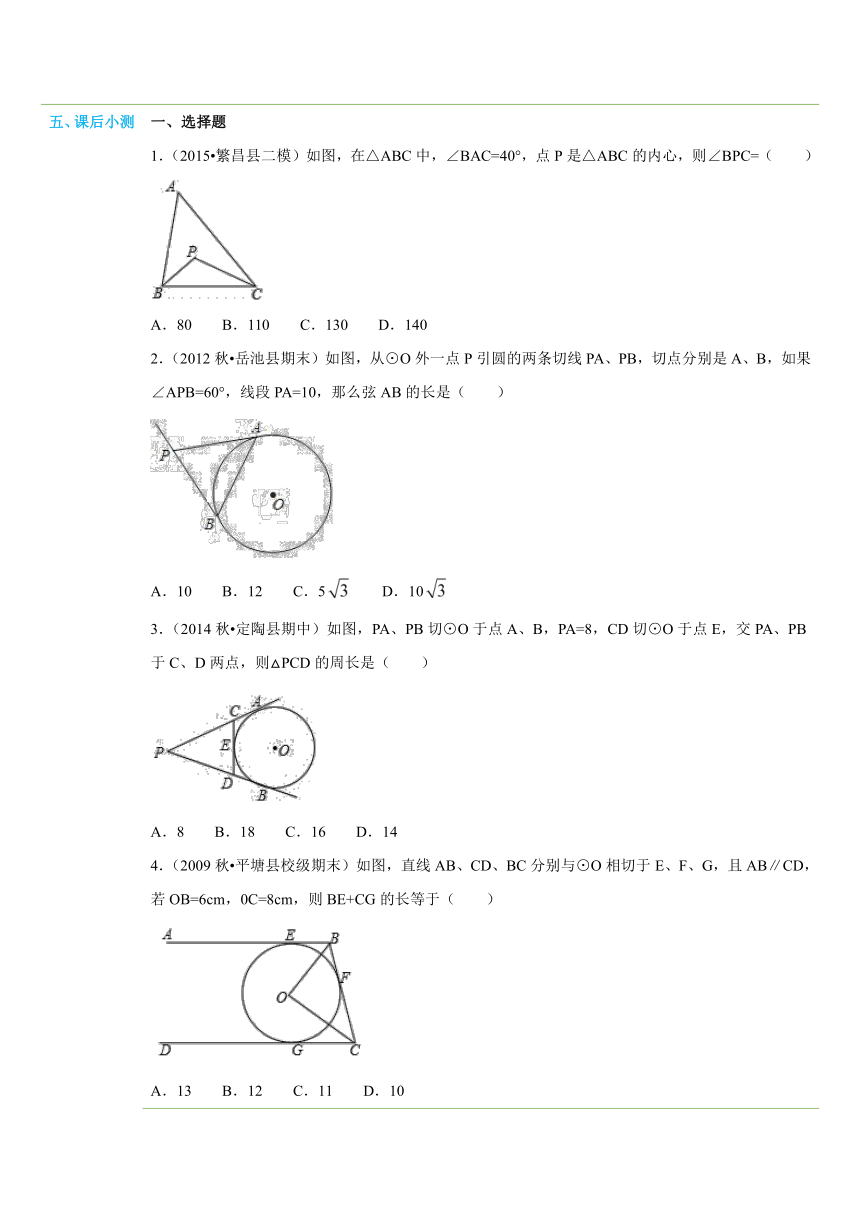
五、课后小测 一、选择题1.(2015 繁昌县二模)如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( ) ( http: / / www.21cnjy.com )A.80 B.110 C.130 D.1402.(2012秋 岳池县期末)如图 ( http: / / www.21cnjy.com ),从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60°,线段PA=10,那么弦AB的长是( ) ( http: / / www.21cnjy.com )A.10 B.12 C.5 D.103.(2014秋 定陶县期中)如图 ( http: / / www.21cnjy.com ),PA、PB切⊙O于点A、B,PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( ) ( http: / / www.21cnjy.com )A.8 B.18 C.16 D.144.(2009秋 平塘县校级期末)如图,直线 ( http: / / www.21cnjy.com )AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,0C=8cm,则BE+CG的长等于( ) ( http: / / www.21cnjy.com )A.13 B.12 C.11 D.105.(2013秋 汉川市期末)如图,⊙O是Rt△ABC的内切圆,∠C=90°,若AC=12cm,BC=9cm,则⊙O的半径( ) ( http: / / www.21cnjy.com )A.3cm B.6cm C.9cm D.15cm6.(2012 杭州模拟)如图,若正△A1B1C1内接于正△ABC的内切圆,则△A1B1C1与△ABC的面积的比值为( ) ( http: / / www.21cnjy.com )A. B. C. D.7.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( ) ( http: / / www.21cnjy.com )A.32 B.34 C.36 D.388.(2015 慈溪市一模)在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.59.(2014春 海曙区校 ( http: / / www.21cnjy.com )级期中)如图,花边带上正三角形的内切圆半径为1cm.如果这条花边带有100个圆和100个正三角形,则这条花边的面积为( ) ( http: / / www.21cnjy.com )A.150π B.150 C.300 D.200二、填空题10.(2013秋 滨湖 ( http: / / www.21cnjy.com )区校级期末)如图示PA、PB是⊙O的切线,切点分别为A、B,直线EF也是⊙O的切线,Q是切点,交PA、PB于E、F点.若PA=10cm,则△PEF的周长为 cm;若∠APB=50°,则∠EOF的度数为 . ( http: / / www.21cnjy.com )11.(2014秋 江阴市期中)如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 . ( http: / / www.21cnjy.com )12.(2012 盘锦模拟)如图,⊙O ( http: / / www.21cnjy.com )内切于△ABC,切点分别为D、E、F,且DE∥BC,若AB=8cm,AD=5cm,则△ADE的周长是 cm. ( http: / / www.21cnjy.com ),三、解答题13.(2011秋 港闸区校级期中)如图,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数. ( http: / / www.21cnjy.com )14.(2013秋 南京期末)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.(1)该三角形的外接圆的半径长等于 ;(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】利用切线长定理可以得到 ( http: / / www.21cnjy.com )AE=AF,BF=BD,CD=CE,因而可以设AF=xcm,BD=ycm,CE=zcm,根据BC=14,AC=9,AB=13,即可得到一个关于x,y,z的方程组,即可求解.
解:设AF=xcm,BD=ycm,CE=zcm.
( http: / / www.21cnjy.com )
∵AF、AE是圆的切线,
∴AE=AF=xcm,
同理:BF=BD=ycm,CD=CE=zcm.
根据题意得:
,
解得:.
即:AF=4,BD=9,CE=5.
故选A.
点评:本题考查了切线长定理,利用切线长定理,把求线段长的问题转化成解方程组的问题,体现了方程思想的运用.
练1.【解析】由于DA、DC、BC都是⊙O的切线,可根据切线长定理,将△PCD的周长转换为PA、PB的长,然后再进行求解.
解:如图,设DC与⊙O的切点为E;
∵PA、PB分别是⊙O的切线,且切点为A、B;
∴PA=PB;
同理,可得:DE=DA,CE=CB;
则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);
∴PA=PB=5cm,
故答案为:5.
点评:此题主要考查了切线长定理的应用,能够将△PCD的周长转换为切线PA、PB的长是解答此题的关键.
【例2】【解析】连接OA,OB,OC,再利用切线长定理,结合三角形内角和定理求解.
解:连接OA、OC、0B,
( http: / / www.21cnjy.com )
∵OA⊥PA,OB⊥PB,OC⊥DE,
∴∠DAO=∠EBO=90°,
∴∠P+∠AOB=180°,
∴∠AOB=180°﹣50°=130°
∵∠AOD=∠DOC,∠COE=∠BOE,
∴∠DOE=∠AOB=×130°=65°.
点评:本题考查了切线长定理,作出有效辅助线是解题的关键.
练2.【解析】由PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,根据切线长定理即可得:CE=CA,DE=DB,然后由等边对等角与三角形外角的性质,可求得∠PAE=∠PCD,∠PBE=∠PDC,继而求得∠PAE+∠PBE的度数.
解:∵PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,
∴CE=CA,DE=DB,
∴∠CAE=∠CEA,∠DEB=∠DBE,
∴∠PCD=∠CAE+∠CEA=2∠CAE,∠PDC=∠DEB+∠DBE=2∠DBE,
∴∠CAE=∠PCD,∠DBE=∠PDC,
即∠PAE=∠PCD,∠PBE=∠PDC,
∵∠P=40°,
∴∠PAE+∠PBE=∠PCD+∠PDC=(∠PCD+∠PDC)=(180°﹣∠P)=70°.
故选D.
点评:此题考查了切线长定理、等腰三角形的性质、三角形外角的性质以及三角形内角和定理.此题难度适中,注意掌握数形结合思想的应用.
【例3】【解析】根据三角形的内角和定理求出∠A,根据多边形的内角和定理求出∠EOF,根据圆周角定理求出∠EDF即可.
解:∵∠A+∠B+∠C=180°,∠B=50°,∠C=60°,
∴∠A=70°,
∵⊙O内切于△ABC,切点分别为D、E、F,
∴∠OEA=∠OFA=90°,
∴∠EOF=360°﹣∠A﹣∠OEA﹣∠OFA=110°,
∴∠EDF=∠EOF=55°.
故选B.
点评:本题主要考查对三角形的内切圆 ( http: / / www.21cnjy.com )与内心,三角形的内角和定理,多边形的内角和定理,圆周角定理等知识点的理解和掌握,能求出∠EOF的度数是解此题的关键.
练3.【解析】本题求的是∠AOB的度数, ( http: / / www.21cnjy.com )而题目却没有明确告诉任何角的度数,因此要从隐含条件入手;CD是AB边上的高,则∠ADC=90°,那么∠BAC+∠ACD=90°;O是△ACD的内心,则AO、CO分别是∠DAC和∠DCA的角平分线,即∠OAC+∠OCA=45°,由此可求得∠AOC的度数;再根据∠AOB和∠AOC的关系,得出∠AOB.
解:如图.连接CO,并延长AO到BC上一点F,
( http: / / www.21cnjy.com )
∵CD为AB边上的高,
∴∠ADC=90°,
∴∠BAC+∠ACD=90°;
又∵O为△ACD的内切圆圆心,
∴AO、CO分别是∠BAC和∠ACD的角平分线,
∴∠OAC+∠OCA=(∠BAC+∠ACD)=×90°=45°,
∴∠AOC=135°;
在△AOB和△AOC中,
,
∴△AOB≌△AOC(SAS),
∴∠AOB=∠AOC=135°.
故答案为:135°.
点评:本题主要考查等腰三角形的性质、 ( http: / / www.21cnjy.com )三角形内切圆的意义、三角形内角和定理、直角三角形的性质;难点在于根据题意画图,由于没任何角的度数,需要充分挖掘隐含条件.此类题学生丢分率较高,需注意.
【例4】【解析】由⊙O是△ABC的内切 ( http: / / www.21cnjy.com )圆,⊙O切AB于E,切BC 于D,根据切线长定理得到AB=AC,A,O,D三点共线,求得BD,AD,BE,AE,由勾股定理列方程求解.
解:如图,∵⊙O是△ABC的内切圆,⊙O切AB于E,切BC 于D,
( http: / / www.21cnjy.com )
∵AB=AC=5,
∴A,O,D三点共线,
∴BD=BC=3,
∴AD==4,
∴BE=BD=3,
∴AE=2,
设三角形内切圆的半径为r,
∴(4-r)2=22+r2,
∴r=cm,
∴三角形内切圆的半径为cm.
故选B.
点评:本题主要考查对三角形的内切圆与内心、切线长定理、切线的性质、勾股定理等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.
练4.【解析】(1)设AB=xcm,则AC=(x+1)cm,根据勾股定理得出方程(x+1)2﹣x2=52,求出x即可;
(2)设内切圆的半径为y,根据三角形面积公式得出S△ABC=×5×12=×5r+×12r+×13r,求出即可.
解:(1)设AB=xcm,则AC=(x+1)cm,
∵在Rt△ABC中,由勾股定理得:AC2﹣AB2=BC2,
∴((x+1)2﹣x2=52,
解得:x=12,
即AB=12cm,AC=13cm;
(2)连接AO、BO、CO、OD、OE、OF,
( http: / / www.21cnjy.com )
设内切圆的半径为y,根据题意,得S△ABC=×5×12=×5r+×12r+×13r,
解得:r=2,
即所求内切圆的半径为2cm.
点评:本题考查了三角形的面积,三角形的内切圆和内心,勾股定理的应用,用了方程思想.
课后小测答案:
一、选择题
1.【解析】解:在△ABC中,∠ABC+∠ACB=180°﹣∠BAC=180°﹣40°=140°,
∵点P是△ABC的内心,
∴∠PBC=∠ABC,∠PCB=ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=×140=70°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180﹣70=110°.
故选B.
2.【解析】解:∵PA、PB都是⊙O的切线,
∴PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,
∴AB=PA=10.
故选A.
3.【解析】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,
∴PB=PA=8,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=16.
故选:C.
4.【解析】解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵CD、BC,AB分别与⊙O相切于G、F、E,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∴BC==10,
∴BE+CG=10(cm).
故选D.
5.【解析】解:如图:连接DO,FO,
( http: / / www.21cnjy.com )
在Rt△ABC,∠C=90°,BC=9cm,AC=12cm,
根据勾股定理AB==15(cm),
四边形OECF中,OD=OF,∠ODC=∠OFC=∠C=90°,
∴四边形OFCD是正方形,
由切线长定理,得:AD=AE,BE=BF,CD=CF,
∴CD=CF=(AC+BC﹣AB),
即r=(9+12﹣15)=3(cm).
故选:A.
6.【解析】解:设圆心为O,AB与圆相切于点D,连接AO,DO,
( http: / / www.21cnjy.com )
∵△A1B1C1和△ABC都是正三角形,
∴它们的内心与外心重合;
如图:设圆的半径为R;
Rt△OAD中,∠OAD=30°,OD=R;
AO=OD =R,
即AB=2R;
同理可求得:A1B1=R,
∴==,
则△A1B1C1与△ABC的面积的比值为:() 2=.
故选:C.
7.【解析】解:由题意可得圆外切四边形的两组对边和相等,
所以四边形的周长=2×(7+10)=34.
故选:B.
8.【解析】解:∵AB=5,AC=3,
( http: / / www.21cnjy.com )
∴BC==4,
∴外接圆半径==2.5,
∵四边形ODCE是正方形,且⊙O是△ABC的内切圆,
∴内切圆半径==1.
故选C.
9.【解析】解:从中选择一个等 ( http: / / www.21cnjy.com )边三角形和其内接圆如图,⊙O是△ABC的内切圆,⊙O切AB于F,切AC于E,切BC于D,连接AD,OB,则AD过O(因为等边三角形的内切圆的圆心再角平分线上,也在底边的垂直平分线上),
( http: / / www.21cnjy.com )
∵△ABC是等边三角形,
∴∠ABC=60°,
∵⊙O是△ABC的内切圆,
∴∠OBC=∠ABC=30°,
∵⊙O切BC于D,
∴∠ODB=90°,
∵OD=1,
∴OB=2,
由勾股定理得:BD==,
∴BC=,
∴S△ABC=BC AD=××3=3.
∴这条花边的面积=100S△ABC=300,
故选C.
二、填空题
10.【解析】解:∵PA、PB是⊙O的切线,
∴PA=PB,
∵EF也是⊙O的切线,
∴EA=EQ,FB=FQ,
∴△PEF的周长=PA+PB=10+10=20cm,
∵∠APB=50°,
∴∠AOB=130°,
∴∠EOF=65°.
故答案为:20,65°.
11.【解析】解:根据勾股定理得:AB==10,
设三角形ABC的内切圆O的半径是r,
∵圆O是直角三角形ABC的内切圆,
∴OD=OE,BF=BD,CD=CE,AE=AF,∠ODC=∠C=∠OEC=90°,
∴四边形ODCE是正方形,
∴OD=OE=CD=CE=r,
∴AC﹣r+BC﹣r=AB,
8﹣r+6﹣r=10,
∴r=2,
故答案为:2.
12.【解析】解:∵AD、AE是圆的切线,
( http: / / www.21cnjy.com )
∴AD=AE,
又∵DE∥BC,
∴,
∴AB=AC,BD=CE.
∵AB=8cm,AD=5cm,
∴BD=AB﹣AD=8﹣5=3cm.
∵BD、BF是圆的切线,
∴BF=BD=3cm,
∴BC=2BF=6cm.
∵DE∥BC,
∴,
∴DE===,
∴△ADE的周长是:5+5+=.
故答案是:.
三、解答题
13.【解析】解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=∠ACD;
同理:∠ODE=∠CDB,
∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
14.【解析】解:(1)在Rt△ACB中,∠C=90°,AC=4,BC=3,
由勾股定理得:AB===5,
即三角形的外接圆的半径长是×5=2.5,
故答案为:2.5.
(2)如图所示:连接OA、OB、OC、OD、OE、OF,
( http: / / www.21cnjy.com )
设内切圆的半径长为r,则OD=OE=OF=r,
由S△OBC+S△OAC+S△OAB=S△ABC,
得:(3r+4r+5r)=×3×4
解得:r=1,
即该三角形内切圆的半径长是1.
二、知识回顾 确定圆的条件是什么?(1)圆心与半径;(2)不在同一直线上的三点.叙述角平分线的性质与判定.性质:角平分线上的点到这个角两边的距离相等.判定:到一个角两边的距离相等的点在这个角的平分线上.和圆有唯一公共点的直线叫圆的切线;圆的切线垂直于过切点的半径.
三、新知讲解 1.切线长经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.几何语言:如图,过圆O外一点P作圆的一条切线,切点为A,则线段PA的长叫做点P到圆O的切线长. ( http: / / www.21cnjy.com )2.切线长定理从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.如图,因为PA、PB是圆O的两条切线,所以:(1)PA=PB;(2)∠APO=∠BPO=∠APB. ( http: / / www.21cnjy.com )3.三角形的内切圆与三角形各边都相切的圆叫做这个三角形的内切圆.这个三角形叫做圆的外切三角形.4.三角形的内心三角形内切圆的圆心叫做三角形的内心,三角形的内心是三角形三条角平分线的交点,这点到三边的距离相等,且必在三角形内部.
四、典例探究 扫一扫,有惊喜哦!1. 应用切线长定理求线段长【例1】(2014 毕节市三模)在三角形 ( http: / / www.21cnjy.com )ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( ) ( http: / / www.21cnjy.com )A.AF=4,BD=9,CE=5 B.AF=4,BD=5,CE=9C.AF=5,BD=4,CE=9 D.AF=9,BD=4,CE=5总结:根据切线长定理,即:“从圆外一点可以引圆的两条切线,它们的切线长相等”,可以得到一些相等线段,结合已知线段之间的关系可以求出线段长.练1.(2014秋 如皋市校级月考)如图, ( http: / / www.21cnjy.com )PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA= cm. ( http: / / www.21cnjy.com )2.应用切线长定理求角度【例2】(2011秋 广东期末)如图,PA、PB、DE切⊙O于点A、B、C、D在PA上,E在PB上,若∠P=50°,求∠O的度数. ( http: / / www.21cnjy.com )总结:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角,也平分圆心和两个切点组成的圆心角.切线长定理为证明线段相等、角相等、垂直关系等提供了理论依据,结合圆周角定理、三角形内角和、等边对等角等性质即可求得角的度数.练2.(2011秋 杭州期末)如图,PA、 ( http: / / www.21cnjy.com )PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=40°,则∠PAE+∠PBE的度数为( ) ( http: / / www.21cnjy.com )0A.50° B.62° C.66° D.70°3.已知三角形内切圆求角度【例3】(2015 宁波校 ( http: / / www.21cnjy.com )级模拟)如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( ) ( http: / / www.21cnjy.com )A.40° B.55° C.65° D.70°总结:1.三角形的内切圆与外接圆的区别:“切”和“接”是指三角形的三边与圆的位置关系,而“内”和“外”是指三角形与圆的相对位置关系.2.已知三角形内切圆,可得垂直关系,以及相等线段和相等角,求线段或角度时要善于利用这些隐含条件.3.三角形的内心就是三角形内切圆的圆心,是三角形三条角平分线的交点,这个对求角度也很重要.练3.(2015 包头一模)如图,△A ( http: / / www.21cnjy.com )BC中,AB=AC,∠A为锐角,CD为AB边上的高,点O为△ACD的内切圆圆心,则∠AOB= . ( http: / / www.21cnjy.com )4.已知三角形边长,求内切圆半径【例4】(2014秋 海门市期末)已知三角形三边长分别为5cm、5cm、6cm,则这个三角形内切圆的半径是( )A.cm B.cm C.2cm D.3cm总结:1. 等腰三角形内切圆半径的求法:作等腰三角形底边上的高,并连接圆心和腰上的切点,构造等腰三角形,通过勾股定理求解.2.直角三角形内切圆半径的求法:设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的内切圆的半径或.3.一般三角形内切圆半径的求法:设△ABC的三边为a、b、c,面积为S,则△ABC的内切圆的半径.练4.(2012秋 新沂市校级期末)如图,在Rt△ABC中,∠ABC=90°,BC=5cm,AC﹣AB=1cm.(1)求AB、AC的长;(2)求△ABC内切圆的半径. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2015 繁昌县二模)如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( ) ( http: / / www.21cnjy.com )A.80 B.110 C.130 D.1402.(2012秋 岳池县期末)如图 ( http: / / www.21cnjy.com ),从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60°,线段PA=10,那么弦AB的长是( ) ( http: / / www.21cnjy.com )A.10 B.12 C.5 D.103.(2014秋 定陶县期中)如图 ( http: / / www.21cnjy.com ),PA、PB切⊙O于点A、B,PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( ) ( http: / / www.21cnjy.com )A.8 B.18 C.16 D.144.(2009秋 平塘县校级期末)如图,直线 ( http: / / www.21cnjy.com )AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,0C=8cm,则BE+CG的长等于( ) ( http: / / www.21cnjy.com )A.13 B.12 C.11 D.105.(2013秋 汉川市期末)如图,⊙O是Rt△ABC的内切圆,∠C=90°,若AC=12cm,BC=9cm,则⊙O的半径( ) ( http: / / www.21cnjy.com )A.3cm B.6cm C.9cm D.15cm6.(2012 杭州模拟)如图,若正△A1B1C1内接于正△ABC的内切圆,则△A1B1C1与△ABC的面积的比值为( ) ( http: / / www.21cnjy.com )A. B. C. D.7.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( ) ( http: / / www.21cnjy.com )A.32 B.34 C.36 D.388.(2015 慈溪市一模)在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.59.(2014春 海曙区校 ( http: / / www.21cnjy.com )级期中)如图,花边带上正三角形的内切圆半径为1cm.如果这条花边带有100个圆和100个正三角形,则这条花边的面积为( ) ( http: / / www.21cnjy.com )A.150π B.150 C.300 D.200二、填空题10.(2013秋 滨湖 ( http: / / www.21cnjy.com )区校级期末)如图示PA、PB是⊙O的切线,切点分别为A、B,直线EF也是⊙O的切线,Q是切点,交PA、PB于E、F点.若PA=10cm,则△PEF的周长为 cm;若∠APB=50°,则∠EOF的度数为 . ( http: / / www.21cnjy.com )11.(2014秋 江阴市期中)如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 . ( http: / / www.21cnjy.com )12.(2012 盘锦模拟)如图,⊙O ( http: / / www.21cnjy.com )内切于△ABC,切点分别为D、E、F,且DE∥BC,若AB=8cm,AD=5cm,则△ADE的周长是 cm. ( http: / / www.21cnjy.com ),三、解答题13.(2011秋 港闸区校级期中)如图,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数. ( http: / / www.21cnjy.com )14.(2013秋 南京期末)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.(1)该三角形的外接圆的半径长等于 ;(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】利用切线长定理可以得到 ( http: / / www.21cnjy.com )AE=AF,BF=BD,CD=CE,因而可以设AF=xcm,BD=ycm,CE=zcm,根据BC=14,AC=9,AB=13,即可得到一个关于x,y,z的方程组,即可求解.
解:设AF=xcm,BD=ycm,CE=zcm.
( http: / / www.21cnjy.com )
∵AF、AE是圆的切线,
∴AE=AF=xcm,
同理:BF=BD=ycm,CD=CE=zcm.
根据题意得:
,
解得:.
即:AF=4,BD=9,CE=5.
故选A.
点评:本题考查了切线长定理,利用切线长定理,把求线段长的问题转化成解方程组的问题,体现了方程思想的运用.
练1.【解析】由于DA、DC、BC都是⊙O的切线,可根据切线长定理,将△PCD的周长转换为PA、PB的长,然后再进行求解.
解:如图,设DC与⊙O的切点为E;
∵PA、PB分别是⊙O的切线,且切点为A、B;
∴PA=PB;
同理,可得:DE=DA,CE=CB;
则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);
∴PA=PB=5cm,
故答案为:5.
点评:此题主要考查了切线长定理的应用,能够将△PCD的周长转换为切线PA、PB的长是解答此题的关键.
【例2】【解析】连接OA,OB,OC,再利用切线长定理,结合三角形内角和定理求解.
解:连接OA、OC、0B,
( http: / / www.21cnjy.com )
∵OA⊥PA,OB⊥PB,OC⊥DE,
∴∠DAO=∠EBO=90°,
∴∠P+∠AOB=180°,
∴∠AOB=180°﹣50°=130°
∵∠AOD=∠DOC,∠COE=∠BOE,
∴∠DOE=∠AOB=×130°=65°.
点评:本题考查了切线长定理,作出有效辅助线是解题的关键.
练2.【解析】由PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,根据切线长定理即可得:CE=CA,DE=DB,然后由等边对等角与三角形外角的性质,可求得∠PAE=∠PCD,∠PBE=∠PDC,继而求得∠PAE+∠PBE的度数.
解:∵PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,
∴CE=CA,DE=DB,
∴∠CAE=∠CEA,∠DEB=∠DBE,
∴∠PCD=∠CAE+∠CEA=2∠CAE,∠PDC=∠DEB+∠DBE=2∠DBE,
∴∠CAE=∠PCD,∠DBE=∠PDC,
即∠PAE=∠PCD,∠PBE=∠PDC,
∵∠P=40°,
∴∠PAE+∠PBE=∠PCD+∠PDC=(∠PCD+∠PDC)=(180°﹣∠P)=70°.
故选D.
点评:此题考查了切线长定理、等腰三角形的性质、三角形外角的性质以及三角形内角和定理.此题难度适中,注意掌握数形结合思想的应用.
【例3】【解析】根据三角形的内角和定理求出∠A,根据多边形的内角和定理求出∠EOF,根据圆周角定理求出∠EDF即可.
解:∵∠A+∠B+∠C=180°,∠B=50°,∠C=60°,
∴∠A=70°,
∵⊙O内切于△ABC,切点分别为D、E、F,
∴∠OEA=∠OFA=90°,
∴∠EOF=360°﹣∠A﹣∠OEA﹣∠OFA=110°,
∴∠EDF=∠EOF=55°.
故选B.
点评:本题主要考查对三角形的内切圆 ( http: / / www.21cnjy.com )与内心,三角形的内角和定理,多边形的内角和定理,圆周角定理等知识点的理解和掌握,能求出∠EOF的度数是解此题的关键.
练3.【解析】本题求的是∠AOB的度数, ( http: / / www.21cnjy.com )而题目却没有明确告诉任何角的度数,因此要从隐含条件入手;CD是AB边上的高,则∠ADC=90°,那么∠BAC+∠ACD=90°;O是△ACD的内心,则AO、CO分别是∠DAC和∠DCA的角平分线,即∠OAC+∠OCA=45°,由此可求得∠AOC的度数;再根据∠AOB和∠AOC的关系,得出∠AOB.
解:如图.连接CO,并延长AO到BC上一点F,
( http: / / www.21cnjy.com )
∵CD为AB边上的高,
∴∠ADC=90°,
∴∠BAC+∠ACD=90°;
又∵O为△ACD的内切圆圆心,
∴AO、CO分别是∠BAC和∠ACD的角平分线,
∴∠OAC+∠OCA=(∠BAC+∠ACD)=×90°=45°,
∴∠AOC=135°;
在△AOB和△AOC中,
,
∴△AOB≌△AOC(SAS),
∴∠AOB=∠AOC=135°.
故答案为:135°.
点评:本题主要考查等腰三角形的性质、 ( http: / / www.21cnjy.com )三角形内切圆的意义、三角形内角和定理、直角三角形的性质;难点在于根据题意画图,由于没任何角的度数,需要充分挖掘隐含条件.此类题学生丢分率较高,需注意.
【例4】【解析】由⊙O是△ABC的内切 ( http: / / www.21cnjy.com )圆,⊙O切AB于E,切BC 于D,根据切线长定理得到AB=AC,A,O,D三点共线,求得BD,AD,BE,AE,由勾股定理列方程求解.
解:如图,∵⊙O是△ABC的内切圆,⊙O切AB于E,切BC 于D,
( http: / / www.21cnjy.com )
∵AB=AC=5,
∴A,O,D三点共线,
∴BD=BC=3,
∴AD==4,
∴BE=BD=3,
∴AE=2,
设三角形内切圆的半径为r,
∴(4-r)2=22+r2,
∴r=cm,
∴三角形内切圆的半径为cm.
故选B.
点评:本题主要考查对三角形的内切圆与内心、切线长定理、切线的性质、勾股定理等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.
练4.【解析】(1)设AB=xcm,则AC=(x+1)cm,根据勾股定理得出方程(x+1)2﹣x2=52,求出x即可;
(2)设内切圆的半径为y,根据三角形面积公式得出S△ABC=×5×12=×5r+×12r+×13r,求出即可.
解:(1)设AB=xcm,则AC=(x+1)cm,
∵在Rt△ABC中,由勾股定理得:AC2﹣AB2=BC2,
∴((x+1)2﹣x2=52,
解得:x=12,
即AB=12cm,AC=13cm;
(2)连接AO、BO、CO、OD、OE、OF,
( http: / / www.21cnjy.com )
设内切圆的半径为y,根据题意,得S△ABC=×5×12=×5r+×12r+×13r,
解得:r=2,
即所求内切圆的半径为2cm.
点评:本题考查了三角形的面积,三角形的内切圆和内心,勾股定理的应用,用了方程思想.
课后小测答案:
一、选择题
1.【解析】解:在△ABC中,∠ABC+∠ACB=180°﹣∠BAC=180°﹣40°=140°,
∵点P是△ABC的内心,
∴∠PBC=∠ABC,∠PCB=ACB,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=×140=70°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180﹣70=110°.
故选B.
2.【解析】解:∵PA、PB都是⊙O的切线,
∴PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,
∴AB=PA=10.
故选A.
3.【解析】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,
∴PB=PA=8,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=16.
故选:C.
4.【解析】解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵CD、BC,AB分别与⊙O相切于G、F、E,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∴BC==10,
∴BE+CG=10(cm).
故选D.
5.【解析】解:如图:连接DO,FO,
( http: / / www.21cnjy.com )
在Rt△ABC,∠C=90°,BC=9cm,AC=12cm,
根据勾股定理AB==15(cm),
四边形OECF中,OD=OF,∠ODC=∠OFC=∠C=90°,
∴四边形OFCD是正方形,
由切线长定理,得:AD=AE,BE=BF,CD=CF,
∴CD=CF=(AC+BC﹣AB),
即r=(9+12﹣15)=3(cm).
故选:A.
6.【解析】解:设圆心为O,AB与圆相切于点D,连接AO,DO,
( http: / / www.21cnjy.com )
∵△A1B1C1和△ABC都是正三角形,
∴它们的内心与外心重合;
如图:设圆的半径为R;
Rt△OAD中,∠OAD=30°,OD=R;
AO=OD =R,
即AB=2R;
同理可求得:A1B1=R,
∴==,
则△A1B1C1与△ABC的面积的比值为:() 2=.
故选:C.
7.【解析】解:由题意可得圆外切四边形的两组对边和相等,
所以四边形的周长=2×(7+10)=34.
故选:B.
8.【解析】解:∵AB=5,AC=3,
( http: / / www.21cnjy.com )
∴BC==4,
∴外接圆半径==2.5,
∵四边形ODCE是正方形,且⊙O是△ABC的内切圆,
∴内切圆半径==1.
故选C.
9.【解析】解:从中选择一个等 ( http: / / www.21cnjy.com )边三角形和其内接圆如图,⊙O是△ABC的内切圆,⊙O切AB于F,切AC于E,切BC于D,连接AD,OB,则AD过O(因为等边三角形的内切圆的圆心再角平分线上,也在底边的垂直平分线上),
( http: / / www.21cnjy.com )
∵△ABC是等边三角形,
∴∠ABC=60°,
∵⊙O是△ABC的内切圆,
∴∠OBC=∠ABC=30°,
∵⊙O切BC于D,
∴∠ODB=90°,
∵OD=1,
∴OB=2,
由勾股定理得:BD==,
∴BC=,
∴S△ABC=BC AD=××3=3.
∴这条花边的面积=100S△ABC=300,
故选C.
二、填空题
10.【解析】解:∵PA、PB是⊙O的切线,
∴PA=PB,
∵EF也是⊙O的切线,
∴EA=EQ,FB=FQ,
∴△PEF的周长=PA+PB=10+10=20cm,
∵∠APB=50°,
∴∠AOB=130°,
∴∠EOF=65°.
故答案为:20,65°.
11.【解析】解:根据勾股定理得:AB==10,
设三角形ABC的内切圆O的半径是r,
∵圆O是直角三角形ABC的内切圆,
∴OD=OE,BF=BD,CD=CE,AE=AF,∠ODC=∠C=∠OEC=90°,
∴四边形ODCE是正方形,
∴OD=OE=CD=CE=r,
∴AC﹣r+BC﹣r=AB,
8﹣r+6﹣r=10,
∴r=2,
故答案为:2.
12.【解析】解:∵AD、AE是圆的切线,
( http: / / www.21cnjy.com )
∴AD=AE,
又∵DE∥BC,
∴,
∴AB=AC,BD=CE.
∵AB=8cm,AD=5cm,
∴BD=AB﹣AD=8﹣5=3cm.
∵BD、BF是圆的切线,
∴BF=BD=3cm,
∴BC=2BF=6cm.
∵DE∥BC,
∴,
∴DE===,
∴△ADE的周长是:5+5+=.
故答案是:.
三、解答题
13.【解析】解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°﹣120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=∠ACD;
同理:∠ODE=∠CDB,
∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,
∴∠COD=180﹣120°=60°.
14.【解析】解:(1)在Rt△ACB中,∠C=90°,AC=4,BC=3,
由勾股定理得:AB===5,
即三角形的外接圆的半径长是×5=2.5,
故答案为:2.5.
(2)如图所示:连接OA、OB、OC、OD、OE、OF,
( http: / / www.21cnjy.com )
设内切圆的半径长为r,则OD=OE=OF=r,
由S△OBC+S△OAC+S△OAB=S△ABC,
得:(3r+4r+5r)=×3×4
解得:r=1,
即该三角形内切圆的半径长是1.
同课章节目录
