【多媒体导学案】人教版数学九年级上册第24章第12课时《弧长》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第12课时《弧长》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 00:00:00 | ||
图片预览




文档简介
一、学习目标 经历探索弧长计算公式的过程;掌握弧长计算公式,并会应用公式解决简单的实际问题.
二、知识回顾 弧的定义是什么?圆上任意两点间的部分叫做圆弧,简称弧.弧长是圆周长的一部分.圆周长的计算公式:C=2πR .
三、新知讲解 弧长公式,其中n°为圆心角的大小,R为圆的半径.推导过程:由360°的圆心角所对的弧长为2πR,可知1°的圆心角所对的弧长为,则n°的圆心角所对的弧长为,所以弧长公式为.
四、典例探究 扫一扫,有惊喜哦!利用弧长公式求弧长【例1】(2011 綦江县)如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,0A=3,那么∠AOB所对弧的长度为( ) ( http: / / www.21cnjy.com )A.6π B.5π C.3π D.2π总结:弧长与弧所对的圆心角、所在圆的半径有关,所以求弧长先要找出或求出弧所对的圆心角及所在圆的半径. 牢记弧长公式是求弧长的关键. 注意:弧长公式中分母是180而不是360.练1.(2010 兴化市校级模拟)某一型 ( http: / / www.21cnjy.com )号挂钟分针的固定点到分针针尖的距离为9cm,从某一时刻起经过20分钟,它的针尖转过的路线长是 cm﹙结果保留π﹚. ( http: / / www.21cnjy.com )已知弧长求圆心角或半径【例2】(2010秋 灌云县校级期末)若扇形的圆心角为100°,弧长为5π,则这条弧所在圆的半径为( )A.7 B.8 C.9 D.10总结:弧长公式中涉及三个变量,分别是弧长、圆心角和半径,已知其中两个量可以求第三个量,注意对公式的变形.练2 .(2008秋 朝阳区期末)在半径为3cm的圆中,长为2πcm的弧所对的圆心角的度数为( )A.30° B.60° C.90° D.120°3.已知弦心距和弦长求弧长【例3】(2014秋 嘉兴校级期中)弦心距为4、弦长为8的弦所对的劣弧长是( )A.π B.4π C.2π D.8π总结:1.求弧长需要两个条件:弧所在圆的半径,弧所对的圆心角,所以求弧长先要求出弧所在圆的半径和弧所对的圆心角.2.已知弦心距和弦长求弧长,先要根据垂径定理求出半径,利用直角三角形的性质求出圆心角.3. 注意:弦所对的弧有两条,如果题中没有注明求优弧还是劣弧,那么分两种情况求解.练3.(2014秋 宁海县月考)如图,圆心角∠AOB=120°,弦AB=2cm.(1)求⊙O的半径r;(2)求劣弧的长(结果保留π). ( http: / / www.21cnjy.com )4.求图形滚动时点经过的路径长【例4】(2015 恩施州)如图,半径为5 ( http: / / www.21cnjy.com )的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 . ( http: / / www.21cnjy.com )总结:求图形滚动过的路径长关键是搞清图形在滚动过程中某点所经过的各段路径,然后逐段求出各段路径的长度,从而求出总的路线长度.练4.如图,边长为a的正方形ABCD的四边 ( http: / / www.21cnjy.com )贴着直线l向右无滑动“滚动”,当正方形“滚动”一周时,该正方形的中心O经过的路程是多少?顶点A经过的路程又是多少? ( http: / / www.21cnjy.com )
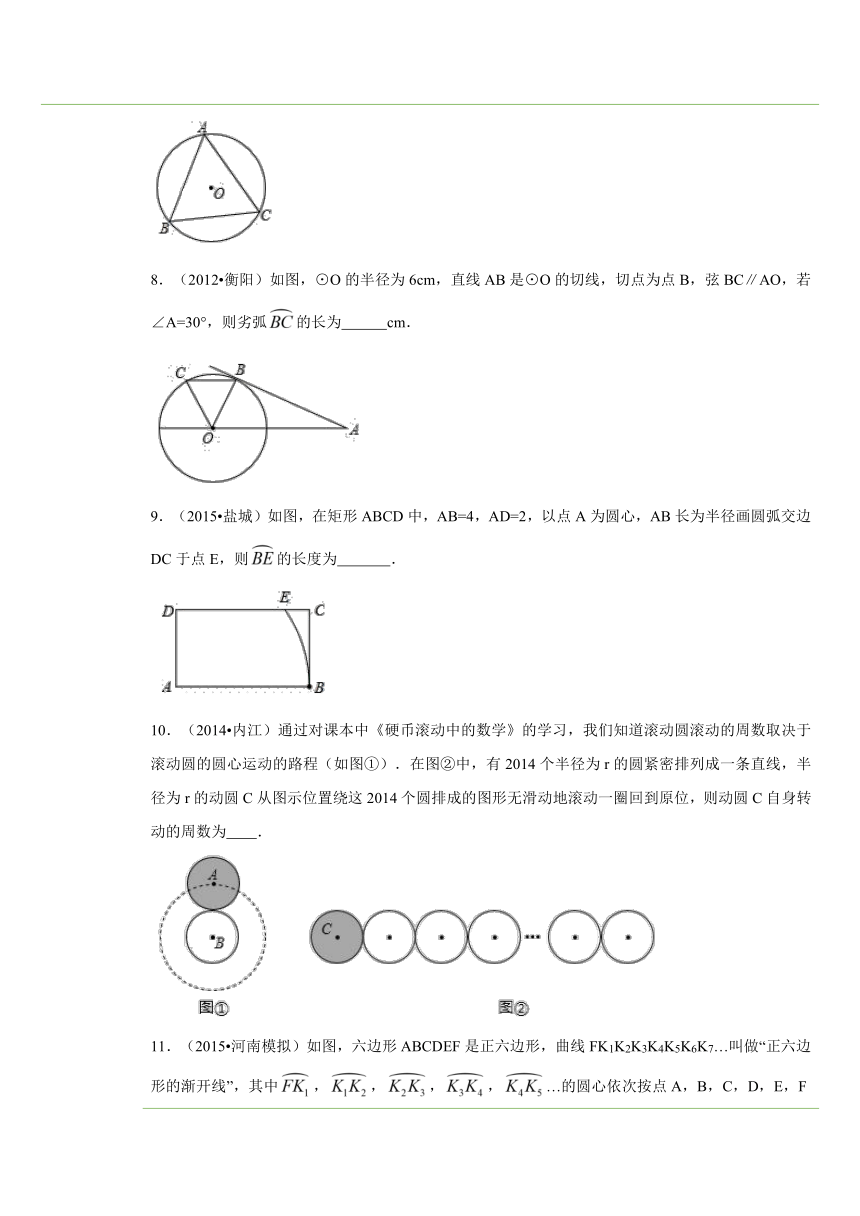
五、课后小测 一、选择题1.(2013 东营)如图 ( http: / / www.21cnjy.com ),正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( ) ( http: / / www.21cnjy.com )A. B. C. D. 2.(2013 凤阳县模拟)如图,⊙O的弦BD垂直平分半径AO,已知OB=3,那么劣弧的长等于( ) ( http: / / www.21cnjy.com )A.12π B.4π C.2π D.π3.(2010 宝坻区一模)一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( ) ( http: / / www.21cnjy.com )A. B. C.4 D.2+4.(2015 杭州模拟)如图,扇形A ( http: / / www.21cnjy.com )OB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为( ) ( http: / / www.21cnjy.com )A.3π B. C. D.4π二、填空题5.(2013河南省)已知扇形的半径为4㎝,圆心角为120°,则此扇形的弧长是____cm.6.(2013 徐州)已知扇形的圆心角为120°,弧长为10πcm,则扇形的半径为 cm.7.(2013秋 海珠区期末)如图,边长为的正三角形ABC内接于⊙O,则AB所对弧ACB的长为 . ( http: / / www.21cnjy.com )8.(2012 衡阳)如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO,若∠A=30°,则劣弧的长为 cm. ( http: / / www.21cnjy.com )9.(2015 盐城)如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则的长度为 . ( http: / / www.21cnjy.com )10.(2014 内江)通过对课本 ( http: / / www.21cnjy.com )中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为 . ( http: / / www.21cnjy.com )11.(2015 河南模拟)如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中,,,,…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于 . ( http: / / www.21cnjy.com )三、解答题12.(2014秋 厦门期中)如图,已知∠ABC=90°,AB=πr,BC=,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图,并求出圆心O运动的路程. ( http: / / www.21cnjy.com )13.如图,△ABC内接于⊙O,AB=cm,∠C=45°,求的长. ( http: / / www.21cnjy.com )14.在周长为300cm的圆周上, ( http: / / www.21cnjy.com )有甲、乙两球以大小不等的速度作匀速运动,甲球从A点出发按顺时针方向运动,乙球同时从B点出发,按逆时针方向运动,两球相遇于C点,相遇后两球各自在圆上反向作匀速运动,但这时甲球速度是原来的2倍,乙球速度是原来的一半,它们第二次相遇于D点,D在AnB上,已知AmC=40cm,BnD=20cm,求ACB的长度. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】解:∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
而∠P=60°,
∴∠AOB=120°,
∠AOB所对弧的长度==2π.
故选D.
练1.【解析】某一型号挂钟分针的固定点到分针 ( http: / / www.21cnjy.com )针尖的距离为9cm即半径为9cm,从某一时刻起经过20分钟,即圆心角是120度,它的针尖转过的路线长就是弧长,所以利用弧长公式就可求出.
解:l==6πcm.
点评:本题重在理解某一型号 ( http: / / www.21cnjy.com )挂钟分针的固定点到分针针尖的距离为9cm即半径为9,从某一时刻起经过20分钟,即圆心角是60度,它的针尖转过的路线长就是弧长.
【例2】【解析】解:设这条弧所在圆的半径为R,
∴5π=,
∴R=9.
故选C.
练2.解:2π=,
解得n=120°.
故选D.
【例3】【解析】首先根据 ( http: / / www.21cnjy.com )题意画出图形,连接OA、OB,再根据垂径定理求出AC=BC=4,推出∠AOB=90°,在Rt△ACO中,由勾股定理求出OA,根据弧长公式求出即可.
解:如图,连接OA、OB,
( http: / / www.21cnjy.com )
∵OC⊥AB,OC过O,AB=8,
∴AC=BC=4,
∵OC=4,
∴AC=BC=OC,
∴∠AOB=90°,
在Rt△ACO中,由勾股定理得:OA==4,
劣弧AB的长是=2π,
故选C.
点评:本题考查了弧长公式,垂径定理,勾股定理的应用,主要考查学生的理解能力和计算能力,注意:半径为R,圆心角为n°所对的弧的长度是l=.
练3.【解析】(1)作OC⊥AB于C,利用垂径定理得到直角三角形,解此直角三角形求得圆的半径即可;
(2)利用上题求得的圆的半径,将其代入弧长的公式求得弧长即可.
解:(1)作OC⊥AB于C,
( http: / / www.21cnjy.com )
则AC=AB=cm.
∵∠AOB=120°,OA=OB,∴∠A=30°.
∴OC=OA,
在Rt△AOC中,,
即,
解得OA=2,
故r=OA=2cm.
(2)劣弧的长为:cm.
点评:本题考查了垂径定理、弧长的计算及解直角三角形的知识,解题的关键是利用垂径定理构造直角三角形.
【例4】【解析】根据题意得出半圆在无滑动旋转中通过的路程分类两段,分别求出各段路径长再求和即可.
解:由图形可知,圆心先向前走OO1的长度,
从O到O1的运动轨迹是一条线段,长度为圆的周长,
然后沿着弧O1O2旋转圆的周长,
则圆心O运动路径的长度为:×2π×5+×2π×5=5π,
( http: / / www.21cnjy.com )
故答案为:5π.
点评:本题考查的是弧长的计算和旋转的知识,解题关键是确定半圆作无滑动翻转所经过的路线并求出长度.
练4.【解析】(1)根据题意,画出正方形ABCD“滚动”一周后中心O所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程;
(2)根据题意,画出正方形ABCD“滚动”一周后顶点A所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程.
解:(1)如图1,正方形ABCD“滚动”一周时,中心O所经过的路程为:
=.
( http: / / www.21cnjy.com )
(2)如图2,正方形ABCD“滚动”一周时,顶点A所经过的路程为:
=.
( http: / / www.21cnjy.com )
点评:本题考查了弧长的计算、正方形的性 ( http: / / www.21cnjy.com )质.在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°.
课后小测答案:
一、选择题
1.解:选A
2.解:∵BC垂直平分AO,
∴OC=AO=OB,
∴∠OBC=30°,∠BOC=60°,
故l劣弧AB==π.
故选D.
3.【解析】根据题目的条件和图形可以判 ( http: / / www.21cnjy.com )断点B分别以C和A为圆心CB和AB为半径旋转120°,并且所走过的两路径相等,求出一个乘以2即可得到.
解:如图:BC=AB=AC=1,
∠BCB′=120°,
∴B点从开始至结束所走过的路径长度为2×弧BB′=2×=,
故选B.
点评:本题考查了弧长的计算方法,求弧长时首先要确定弧所对的圆心角和半径,利用公式求得即可.
4.解:∵D为AC的中点,AC=AO=6,
( http: / / www.21cnjy.com )
∴OD⊥AC,
∴AD=AO,
∴∠AOD=30°,OD=3,
同理可得:∠BOE=30°,
∴∠DOE=150°﹣60°=90°
∴点D所经过路径长为:==.
故选C.
二、填空题
5. 【解析】运用弧长计算公式,将其变形即可求出扇形的半径.
解:扇形的弧长公式是L==,解得r=15.
点评:此题主要考查了扇形的弧长公式的变形,难度不大,计算应认真.
6. 解析:由扇形的弧长公式可得:弧长.
故填:.
7.解:连结OA、OB,作OH⊥AB于H,如图,
( http: / / www.21cnjy.com )
∵△ABC为等边三角形,
∴∠AOB=120°,
∵OH⊥AB,
∴∠AOH=60°,AH=BH=AB=×2=,
∴OH=AH=1,
∴OA=2,
∴AB所对弧ACB的长度==π.
故答案为π.
8.解:∵直线AB是⊙O的切线,
∴OB⊥AB,
又∵∠A=30°,
∴∠BOA=60°,
∵弦BC∥AO,OB=OC,
∴△OBC是等边三角形,
即可得∠BOC=60°,
∴劣弧的长==2πcm.
故答案为:2π.
9.解:连接AE,
( http: / / www.21cnjy.com )
在Rt三角形ADE中,AE=4,AD=2,
∴∠DEA=30°,
∵AB∥CD,
∴∠EAB=∠DEA=30°,
∴的长度为:=,
故答案为:.
10.【解析】它从A位置开始,滚过 ( http: / / www.21cnjy.com )与它相同的其他2014个圆的上部,到达最后位置.则该圆共滚过了2014段弧长,其中有2段是半径为2r,圆心角为120度,2012段是半径为2r,圆心角为60度的弧长,所以可求得.
解:弧长==1344πr,
又因为是来回所以总路程为:1344π×2=2688π,
所以动圆C自身转动的周数为:2688πr÷2πr=1344,
故答案为:1344.
点评:本题考查了弧长的计算.关键是求出动圆C自身转动的长度.
11.解:如图,∵六边形ABCDEF是正六边形,
( http: / / www.21cnjy.com )
∴∠FAK1=180°﹣120°=60°;同理可求l2、l3…l2012的圆心角均为60°
∴,,,
∴可以猜测:,
∴.
故答案为.
三、解答题
12.解:如图:
( http: / / www.21cnjy.com )
圆心O运动的路程长=OD+弧DE的长+EF=AB+弧DE的长+BC=πr++=2πr.
13.解:如图,∵∠C=45°,
∴∠AOB=2∠C=90°,
又∵OA=OB,
∴由勾股定理得OA=AB=3.
∴的长为:=π.
14.【解析】本题考查的知识点是方程的构 ( http: / / www.21cnjy.com )造与应用,要求ACB的长度,由AmC=40厘米,我们只要求出BC长即可,我们不妨设BC=x厘米,甲球速度为v甲,乙球速度为v乙.然后根据相遇问题中时间相等,构造两次相遇时的方程,解方程组即可求出答案.
解:设BC=x厘米.
甲球速度为v甲,乙球速度为v乙.
根据二次从出发到相遇二球运动的时间都相同,
可得第一次等候时方程
第二次等候时方程.
由此可得,
(x﹣40)(x﹣80)=0.
由于已知条件v甲≠v乙,
∴x≠40,
x=80(厘米)
ACB=40+80=120(厘米).
点评:本题考查了弧长的计算,方程与函 ( http: / / www.21cnjy.com )数思想是中学阶段的四大数学思想之一,在利用方程思想解决问题时,我们要解决两个问题:一是谁是未知数,一般由“求谁设谁”的原则来决定;二是找等量关系,如本题中相遇问题的时间相等.并由些构造方程,进行求解.
二、知识回顾 弧的定义是什么?圆上任意两点间的部分叫做圆弧,简称弧.弧长是圆周长的一部分.圆周长的计算公式:C=2πR .
三、新知讲解 弧长公式,其中n°为圆心角的大小,R为圆的半径.推导过程:由360°的圆心角所对的弧长为2πR,可知1°的圆心角所对的弧长为,则n°的圆心角所对的弧长为,所以弧长公式为.
四、典例探究 扫一扫,有惊喜哦!利用弧长公式求弧长【例1】(2011 綦江县)如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,0A=3,那么∠AOB所对弧的长度为( ) ( http: / / www.21cnjy.com )A.6π B.5π C.3π D.2π总结:弧长与弧所对的圆心角、所在圆的半径有关,所以求弧长先要找出或求出弧所对的圆心角及所在圆的半径. 牢记弧长公式是求弧长的关键. 注意:弧长公式中分母是180而不是360.练1.(2010 兴化市校级模拟)某一型 ( http: / / www.21cnjy.com )号挂钟分针的固定点到分针针尖的距离为9cm,从某一时刻起经过20分钟,它的针尖转过的路线长是 cm﹙结果保留π﹚. ( http: / / www.21cnjy.com )已知弧长求圆心角或半径【例2】(2010秋 灌云县校级期末)若扇形的圆心角为100°,弧长为5π,则这条弧所在圆的半径为( )A.7 B.8 C.9 D.10总结:弧长公式中涉及三个变量,分别是弧长、圆心角和半径,已知其中两个量可以求第三个量,注意对公式的变形.练2 .(2008秋 朝阳区期末)在半径为3cm的圆中,长为2πcm的弧所对的圆心角的度数为( )A.30° B.60° C.90° D.120°3.已知弦心距和弦长求弧长【例3】(2014秋 嘉兴校级期中)弦心距为4、弦长为8的弦所对的劣弧长是( )A.π B.4π C.2π D.8π总结:1.求弧长需要两个条件:弧所在圆的半径,弧所对的圆心角,所以求弧长先要求出弧所在圆的半径和弧所对的圆心角.2.已知弦心距和弦长求弧长,先要根据垂径定理求出半径,利用直角三角形的性质求出圆心角.3. 注意:弦所对的弧有两条,如果题中没有注明求优弧还是劣弧,那么分两种情况求解.练3.(2014秋 宁海县月考)如图,圆心角∠AOB=120°,弦AB=2cm.(1)求⊙O的半径r;(2)求劣弧的长(结果保留π). ( http: / / www.21cnjy.com )4.求图形滚动时点经过的路径长【例4】(2015 恩施州)如图,半径为5 ( http: / / www.21cnjy.com )的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 . ( http: / / www.21cnjy.com )总结:求图形滚动过的路径长关键是搞清图形在滚动过程中某点所经过的各段路径,然后逐段求出各段路径的长度,从而求出总的路线长度.练4.如图,边长为a的正方形ABCD的四边 ( http: / / www.21cnjy.com )贴着直线l向右无滑动“滚动”,当正方形“滚动”一周时,该正方形的中心O经过的路程是多少?顶点A经过的路程又是多少? ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2013 东营)如图 ( http: / / www.21cnjy.com ),正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( ) ( http: / / www.21cnjy.com )A. B. C. D. 2.(2013 凤阳县模拟)如图,⊙O的弦BD垂直平分半径AO,已知OB=3,那么劣弧的长等于( ) ( http: / / www.21cnjy.com )A.12π B.4π C.2π D.π3.(2010 宝坻区一模)一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( ) ( http: / / www.21cnjy.com )A. B. C.4 D.2+4.(2015 杭州模拟)如图,扇形A ( http: / / www.21cnjy.com )OB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为( ) ( http: / / www.21cnjy.com )A.3π B. C. D.4π二、填空题5.(2013河南省)已知扇形的半径为4㎝,圆心角为120°,则此扇形的弧长是____cm.6.(2013 徐州)已知扇形的圆心角为120°,弧长为10πcm,则扇形的半径为 cm.7.(2013秋 海珠区期末)如图,边长为的正三角形ABC内接于⊙O,则AB所对弧ACB的长为 . ( http: / / www.21cnjy.com )8.(2012 衡阳)如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO,若∠A=30°,则劣弧的长为 cm. ( http: / / www.21cnjy.com )9.(2015 盐城)如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则的长度为 . ( http: / / www.21cnjy.com )10.(2014 内江)通过对课本 ( http: / / www.21cnjy.com )中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为 . ( http: / / www.21cnjy.com )11.(2015 河南模拟)如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中,,,,…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于 . ( http: / / www.21cnjy.com )三、解答题12.(2014秋 厦门期中)如图,已知∠ABC=90°,AB=πr,BC=,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.请你根据题意,在图上画出圆心O运动路径的示意图,并求出圆心O运动的路程. ( http: / / www.21cnjy.com )13.如图,△ABC内接于⊙O,AB=cm,∠C=45°,求的长. ( http: / / www.21cnjy.com )14.在周长为300cm的圆周上, ( http: / / www.21cnjy.com )有甲、乙两球以大小不等的速度作匀速运动,甲球从A点出发按顺时针方向运动,乙球同时从B点出发,按逆时针方向运动,两球相遇于C点,相遇后两球各自在圆上反向作匀速运动,但这时甲球速度是原来的2倍,乙球速度是原来的一半,它们第二次相遇于D点,D在AnB上,已知AmC=40cm,BnD=20cm,求ACB的长度. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【解析】解:∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
而∠P=60°,
∴∠AOB=120°,
∠AOB所对弧的长度==2π.
故选D.
练1.【解析】某一型号挂钟分针的固定点到分针 ( http: / / www.21cnjy.com )针尖的距离为9cm即半径为9cm,从某一时刻起经过20分钟,即圆心角是120度,它的针尖转过的路线长就是弧长,所以利用弧长公式就可求出.
解:l==6πcm.
点评:本题重在理解某一型号 ( http: / / www.21cnjy.com )挂钟分针的固定点到分针针尖的距离为9cm即半径为9,从某一时刻起经过20分钟,即圆心角是60度,它的针尖转过的路线长就是弧长.
【例2】【解析】解:设这条弧所在圆的半径为R,
∴5π=,
∴R=9.
故选C.
练2.解:2π=,
解得n=120°.
故选D.
【例3】【解析】首先根据 ( http: / / www.21cnjy.com )题意画出图形,连接OA、OB,再根据垂径定理求出AC=BC=4,推出∠AOB=90°,在Rt△ACO中,由勾股定理求出OA,根据弧长公式求出即可.
解:如图,连接OA、OB,
( http: / / www.21cnjy.com )
∵OC⊥AB,OC过O,AB=8,
∴AC=BC=4,
∵OC=4,
∴AC=BC=OC,
∴∠AOB=90°,
在Rt△ACO中,由勾股定理得:OA==4,
劣弧AB的长是=2π,
故选C.
点评:本题考查了弧长公式,垂径定理,勾股定理的应用,主要考查学生的理解能力和计算能力,注意:半径为R,圆心角为n°所对的弧的长度是l=.
练3.【解析】(1)作OC⊥AB于C,利用垂径定理得到直角三角形,解此直角三角形求得圆的半径即可;
(2)利用上题求得的圆的半径,将其代入弧长的公式求得弧长即可.
解:(1)作OC⊥AB于C,
( http: / / www.21cnjy.com )
则AC=AB=cm.
∵∠AOB=120°,OA=OB,∴∠A=30°.
∴OC=OA,
在Rt△AOC中,,
即,
解得OA=2,
故r=OA=2cm.
(2)劣弧的长为:cm.
点评:本题考查了垂径定理、弧长的计算及解直角三角形的知识,解题的关键是利用垂径定理构造直角三角形.
【例4】【解析】根据题意得出半圆在无滑动旋转中通过的路程分类两段,分别求出各段路径长再求和即可.
解:由图形可知,圆心先向前走OO1的长度,
从O到O1的运动轨迹是一条线段,长度为圆的周长,
然后沿着弧O1O2旋转圆的周长,
则圆心O运动路径的长度为:×2π×5+×2π×5=5π,
( http: / / www.21cnjy.com )
故答案为:5π.
点评:本题考查的是弧长的计算和旋转的知识,解题关键是确定半圆作无滑动翻转所经过的路线并求出长度.
练4.【解析】(1)根据题意,画出正方形ABCD“滚动”一周后中心O所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程;
(2)根据题意,画出正方形ABCD“滚动”一周后顶点A所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程.
解:(1)如图1,正方形ABCD“滚动”一周时,中心O所经过的路程为:
=.
( http: / / www.21cnjy.com )
(2)如图2,正方形ABCD“滚动”一周时,顶点A所经过的路程为:
=.
( http: / / www.21cnjy.com )
点评:本题考查了弧长的计算、正方形的性 ( http: / / www.21cnjy.com )质.在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°.
课后小测答案:
一、选择题
1.解:选A
2.解:∵BC垂直平分AO,
∴OC=AO=OB,
∴∠OBC=30°,∠BOC=60°,
故l劣弧AB==π.
故选D.
3.【解析】根据题目的条件和图形可以判 ( http: / / www.21cnjy.com )断点B分别以C和A为圆心CB和AB为半径旋转120°,并且所走过的两路径相等,求出一个乘以2即可得到.
解:如图:BC=AB=AC=1,
∠BCB′=120°,
∴B点从开始至结束所走过的路径长度为2×弧BB′=2×=,
故选B.
点评:本题考查了弧长的计算方法,求弧长时首先要确定弧所对的圆心角和半径,利用公式求得即可.
4.解:∵D为AC的中点,AC=AO=6,
( http: / / www.21cnjy.com )
∴OD⊥AC,
∴AD=AO,
∴∠AOD=30°,OD=3,
同理可得:∠BOE=30°,
∴∠DOE=150°﹣60°=90°
∴点D所经过路径长为:==.
故选C.
二、填空题
5. 【解析】运用弧长计算公式,将其变形即可求出扇形的半径.
解:扇形的弧长公式是L==,解得r=15.
点评:此题主要考查了扇形的弧长公式的变形,难度不大,计算应认真.
6. 解析:由扇形的弧长公式可得:弧长.
故填:.
7.解:连结OA、OB,作OH⊥AB于H,如图,
( http: / / www.21cnjy.com )
∵△ABC为等边三角形,
∴∠AOB=120°,
∵OH⊥AB,
∴∠AOH=60°,AH=BH=AB=×2=,
∴OH=AH=1,
∴OA=2,
∴AB所对弧ACB的长度==π.
故答案为π.
8.解:∵直线AB是⊙O的切线,
∴OB⊥AB,
又∵∠A=30°,
∴∠BOA=60°,
∵弦BC∥AO,OB=OC,
∴△OBC是等边三角形,
即可得∠BOC=60°,
∴劣弧的长==2πcm.
故答案为:2π.
9.解:连接AE,
( http: / / www.21cnjy.com )
在Rt三角形ADE中,AE=4,AD=2,
∴∠DEA=30°,
∵AB∥CD,
∴∠EAB=∠DEA=30°,
∴的长度为:=,
故答案为:.
10.【解析】它从A位置开始,滚过 ( http: / / www.21cnjy.com )与它相同的其他2014个圆的上部,到达最后位置.则该圆共滚过了2014段弧长,其中有2段是半径为2r,圆心角为120度,2012段是半径为2r,圆心角为60度的弧长,所以可求得.
解:弧长==1344πr,
又因为是来回所以总路程为:1344π×2=2688π,
所以动圆C自身转动的周数为:2688πr÷2πr=1344,
故答案为:1344.
点评:本题考查了弧长的计算.关键是求出动圆C自身转动的长度.
11.解:如图,∵六边形ABCDEF是正六边形,
( http: / / www.21cnjy.com )
∴∠FAK1=180°﹣120°=60°;同理可求l2、l3…l2012的圆心角均为60°
∴,,,
∴可以猜测:,
∴.
故答案为.
三、解答题
12.解:如图:
( http: / / www.21cnjy.com )
圆心O运动的路程长=OD+弧DE的长+EF=AB+弧DE的长+BC=πr++=2πr.
13.解:如图,∵∠C=45°,
∴∠AOB=2∠C=90°,
又∵OA=OB,
∴由勾股定理得OA=AB=3.
∴的长为:=π.
14.【解析】本题考查的知识点是方程的构 ( http: / / www.21cnjy.com )造与应用,要求ACB的长度,由AmC=40厘米,我们只要求出BC长即可,我们不妨设BC=x厘米,甲球速度为v甲,乙球速度为v乙.然后根据相遇问题中时间相等,构造两次相遇时的方程,解方程组即可求出答案.
解:设BC=x厘米.
甲球速度为v甲,乙球速度为v乙.
根据二次从出发到相遇二球运动的时间都相同,
可得第一次等候时方程
第二次等候时方程.
由此可得,
(x﹣40)(x﹣80)=0.
由于已知条件v甲≠v乙,
∴x≠40,
x=80(厘米)
ACB=40+80=120(厘米).
点评:本题考查了弧长的计算,方程与函 ( http: / / www.21cnjy.com )数思想是中学阶段的四大数学思想之一,在利用方程思想解决问题时,我们要解决两个问题:一是谁是未知数,一般由“求谁设谁”的原则来决定;二是找等量关系,如本题中相遇问题的时间相等.并由些构造方程,进行求解.
同课章节目录
