【多媒体导学案】人教版数学九年级上册第24章第13课时《扇形面积》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第13课时《扇形面积》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 356.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 00:00:00 | ||
图片预览



文档简介
24-13 扇形面积 人教九上
一、学习目标 1.经历探索扇形面积计算公式的过程;2.了解扇形面积计算公式,并会用公式解决问题;3.了解弧长和扇形面积的关系.
二、知识回顾 1.圆的周长2πR可以看作 360 度的圆心角所对的弧(圆的半径为R). 当圆的半径为R时,1°的圆心角所对的弧长是 ;2°的圆心角所对的弧长是 ;60°的圆心角所对的弧长是 ;n°的圆心角所对的弧长是 ;结论:半径为R的圆中,n°的圆心角所对的弧长为.注意:进行计算时,要注意公式中n的意义,n表示1°的圆心角的倍数,它是不带单位的.
三、新知讲解 1.扇形由 组成圆心角的两条半径和圆心角所对的弧 所围成的图形叫做扇形.2.扇形的面积在半径为R的圆中,因为360°的圆心角所对的扇形面积就是圆的面积S=πR2,所以圆心角是1°的扇形面积是 .于是,圆心角为n°的扇形面积是 .因为n°的圆心角所对的弧长为,所以=.3.阴影部分面积的四种求法(1)公式法:当已知图形为我们熟知的基本图形或将图形分割成几个可直接利用公式求面积的图形时,我们可直接利用有关面积公式求解.(2)等积变换法:把所求阴影部分的图形适当进行等积变形,即找出与它面积相等的特殊图形,从而求出阴影部分图形的面积.(3)整体法:当阴影部分图形为分散的个体时,可针对其结构特征,视各阴影部分图形为一个整体,然后利用相关图形的面积公式整体求出.(4)割补法:将一个图形的一部分割下来,移动到其他合适的位置上,从而构成易求面积的图形.
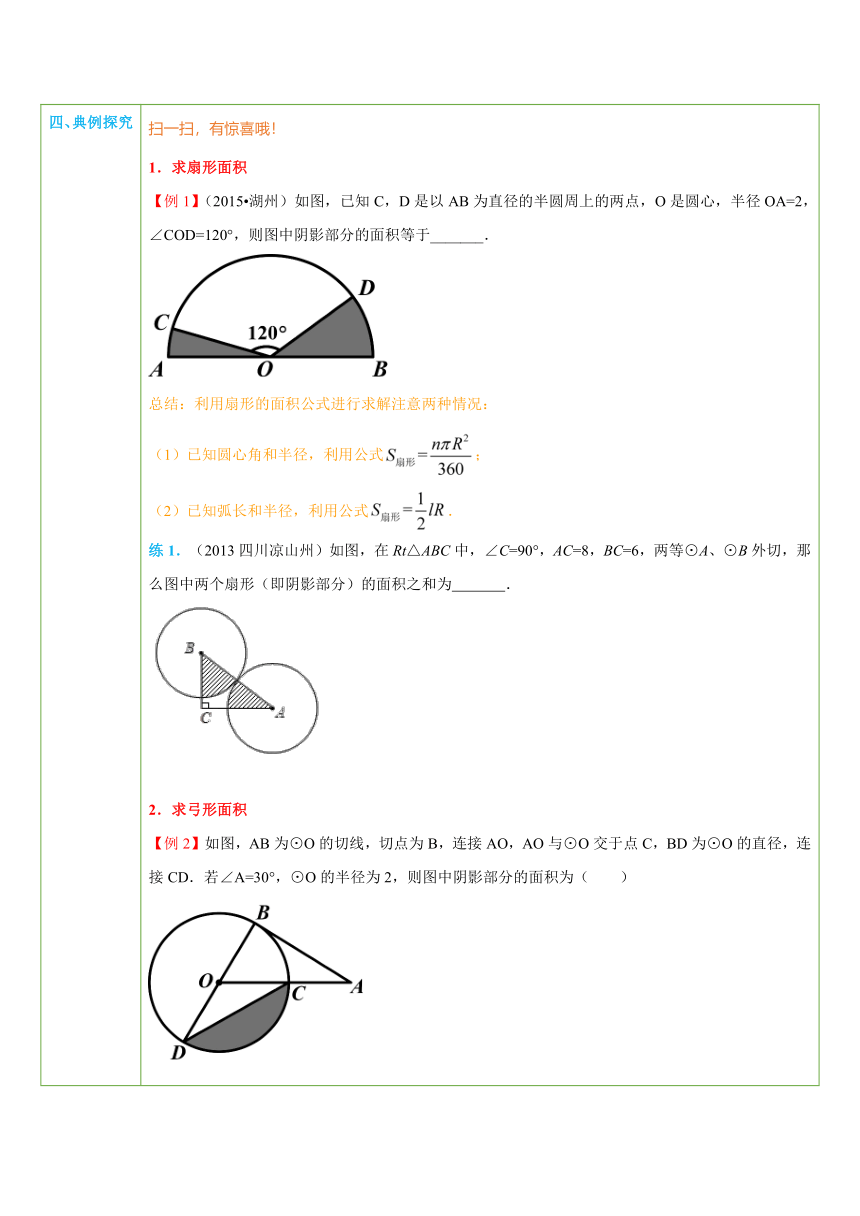
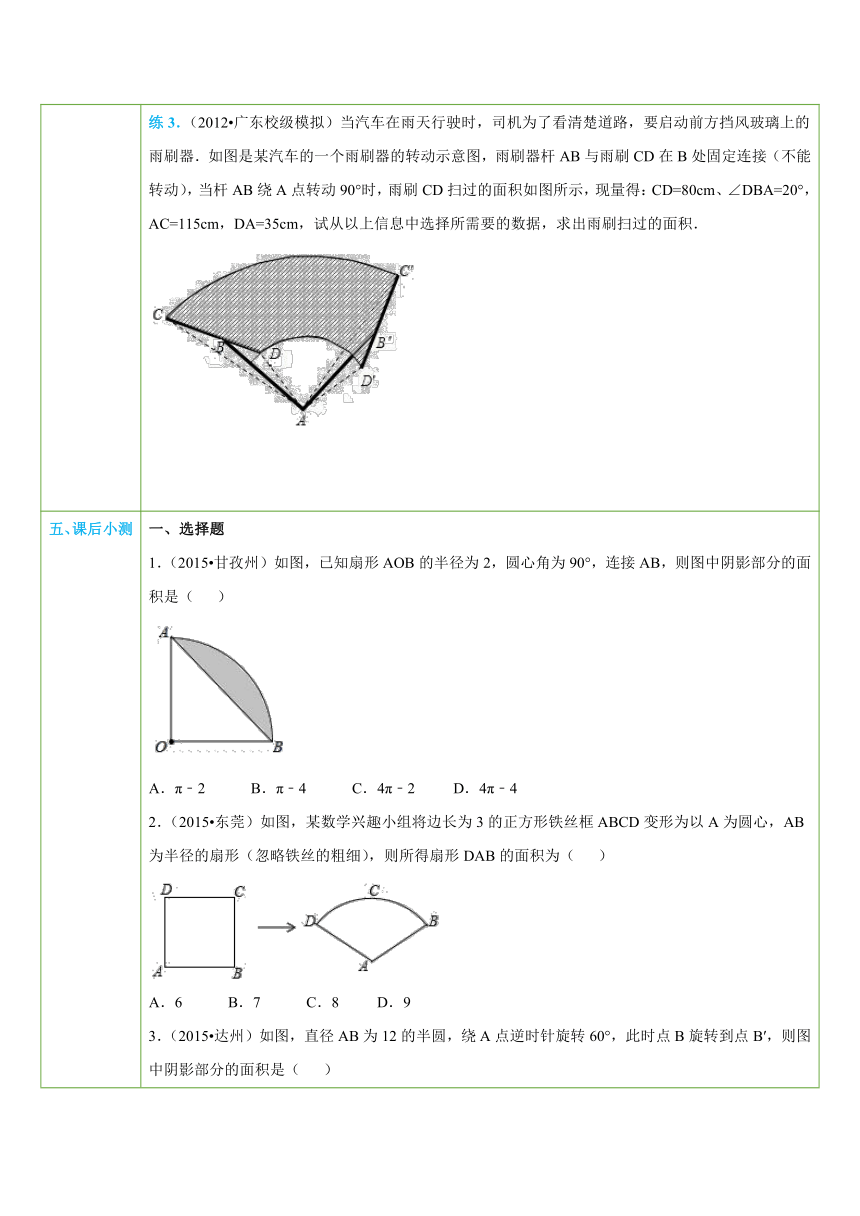
四、典例探究 扫一扫,有惊喜哦!1.求扇形面积【例1】(2015 湖州)如图,已知C, ( http: / / www.21cnjy.com )D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______. ( http: / / www.21cnjy.com )总结:利用扇形的面积公式进行求解注意两种情况:(1)已知圆心角和半径,利用公式;(2)已知弧长和半径,利用公式.练1.(2013四川凉山州)如图,在Rt△ ( http: / / www.21cnjy.com )ABC中,∠C=90°,AC=8,BC=6,两等⊙A、⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为 . ( http: / / www.21cnjy.com )2.求弓形面积【例2】如图,AB为⊙O的切线,切点为B, ( http: / / www.21cnjy.com )连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( ) ( http: / / www.21cnjy.com )A. B. C. D.总结:求弓形的面积一般是转化为求扇形面积与三角形面积的差.求弓形面积时,一般要用到垂径定理,所以过圆心作弦的垂线段是常见的辅助线.练2.(2015 福州校级质检)如图,AB为⊙O的直径,弦AC=2,∠B=30°,∠ACB的平分线交⊙O于点D,求:(1)BC、AD的长;(2)图中两阴影部分面积的和. ( http: / / www.21cnjy.com )3.求图形绕某点旋转后扫过的面积【例3】(2015 永州) ( http: / / www.21cnjy.com )如图,在平面直角坐标系中,点A的坐标(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为_____. ( http: / / www.21cnjy.com )总结:求图形绕某点旋转后扫过的图形面积 ( http: / / www.21cnjy.com ),先要根据运动轨迹分析出扫过的图形的形状,然后根据图形形状求解面积.如果是规则图形,就利用规则图形的公式进行计算;如果是不规则图形,要先转化为规则图形.不规则图形转化为规则图形的方法有:等积变换法.对所求图形进行适当等积变形,即找到与它面积相等的规则图形;割补法.对所求图形进行适当分割,并将一部分图形移位,组成规则图形;.练3.(2012 广东校级模拟)当 ( http: / / www.21cnjy.com )汽车在雨天行驶时,司机为了看清楚道路,要启动前方挡风玻璃上的雨刷器.如图是某汽车的一个雨刷器的转动示意图,雨刷器杆AB与雨刷CD在B处固定连接(不能转动),当杆AB绕A点转动90°时,雨刷CD扫过的面积如图所示,现量得:CD=80cm、∠DBA=20°,AC=115cm,DA=35cm,试从以上信息中选择所需要的数据,求出雨刷扫过的面积. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2015 甘孜州)如图,已知扇形AOB的半径为2,圆心角为90°,连接AB,则图中阴影部分的面积是( ) ( http: / / www.21cnjy.com )A.π﹣2 B.π﹣4 C.4π﹣2 D.4π﹣42.(2015 东莞)如图,某数学 ( http: / / www.21cnjy.com )兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( ) ( http: / / www.21cnjy.com )A.6 B.7 C.8 D.93.(2015 达州)如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( ) ( http: / / www.21cnjy.com )A.12π B.24π C.6π D.36π4.(2015 咸宁)如图,在△ABC中,C ( http: / / www.21cnjy.com )A=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( ) ( http: / / www.21cnjy.com )A.由小到大 B.由大到小C.不变 D.先由小到大,后由大到小二、填空题5.(2015 泰州)圆心角为120°,半径长为6cm的扇形面积是______cm2.6.(2015 常州)已知扇形的圆心角为120°,弧长为6π,则扇形的面积是________.7.(2014 洛阳二模) ( http: / / www.21cnjy.com )如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为__________. ( http: / / www.21cnjy.com )8.(2011 高淳县一 ( http: / / www.21cnjy.com )模)如图,两个半径为2cm的等圆互相重叠,且各自的圆心都在另一个圆上,则两圆重叠部分的面积是_______cm2.(结果保留π). ( http: / / www.21cnjy.com )9.(2012 黄陂区校级模拟)如图, ( http: / / www.21cnjy.com )把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O1A⊥O2A,则图中阴影部分的面积是________. ( http: / / www.21cnjy.com )10.(2015 安顺)如图,在 AB ( http: / / www.21cnjy.com )CD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是_________(结果保留π). ( http: / / www.21cnjy.com )11.(2015 江阴市校级一模) ( http: / / www.21cnjy.com )如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA,OB,OC,OD的中点,若⊙O的半径为2,则阴影部分的面积为__________. ( http: / / www.21cnjy.com )12.(2015 东莞模拟)如图是圆心角 ( http: / / www.21cnjy.com )为30°,半径分别是1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为S1、S2、S3、…,则Sn=_________.(结果保留π) ( http: / / www.21cnjy.com )三、解答题13.(2013 路南区一模)如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π). ( http: / / www.21cnjy.com )14.(2013秋 章丘市校级期末)如图,两个同心圆的半径分别为18cm和30cm,又知∠COD=30°,求阴影部分ABDC的面积. ( http: / / www.21cnjy.com )15.(2013秋 海门市校级期中) ( http: / / www.21cnjy.com )如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积. ( http: / / www.21cnjy.com )16.(2012 云和县模拟)一个商标 ( http: / / www.21cnjy.com )图案如图,矩形ABCD中,AB=2BC,且AB=8cm,以A为圆心,AD长为半径作半圆,求商标图案的面积. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【分析】图中阴影部分的面积=半圆的面积﹣圆心角是120°的扇形的面积,根据扇形面积的计算公式计算即可求解.
【解答】解:图中阴影部分的面积=π×22﹣=2π﹣π=π.
答:图中阴影部分的面积等于π.
故答案为:π.
【点评】考查了扇形面积的计算,求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.
练1.解:
【例2】【分析】过O点作OE⊥ ( http: / / www.21cnjy.com )CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积﹣三角形OCD的面积,列式计算即可求解.
【解答】解:过O点作OE⊥CD于E,
( http: / / www.21cnjy.com )
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:﹣×2×1=π﹣.
故选:A.
【点评】本题考查了扇形面积的计算,切线的性质,解题的关键是理解阴影部分的面积=扇形OCD的面积﹣三角形OCD的面积.
练2.【分析】(1)根据直径得出∠ACB=∠ADB=90°,根据勾股定理求出BC,根据圆周角定理求出AD=BD,求出AD即可;
(2)根据三角形的面积公式,求出△AOC和△AOD的面积,再求出S扇形COD,即可求出答案.
【解答】解:(1)∵AB是直径,
∴∠ACB=∠ADB=90°(直径所对的圆周角是直角),
在Rt△ABC中,∠B=30°,AC=2,
∴AB=4,
∴BC==2,
∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD
∴=,
∴AD=BD,
∴在Rt△ABD中,AD=BD=AB=2;
(2)连接OC,OD,
( http: / / www.21cnjy.com )
∵∠B=30°,
∴∠AOC=∠2∠B=60°,
∵OA=OB,
∴S△AOC=S△ABC=××AC×BC=××2×2=,
由(1)得∠AOD=90°,
∴∠COD=150°,
S△AOD=×AO×OD=×22=2,
∴S阴影=S扇形COD﹣S△AOC﹣S△AOD=﹣﹣2=π﹣﹣2.
【点评】本题考查了勾股定理、圆周角定理 ( http: / / www.21cnjy.com )、三角形的面积等知识点的应用,关键是求出∠ACB=∠ADB=90°,题型较好,通过做此题,培养了学生运用定理进行推理的能力.
【例3】【分析】根据点A的坐标(﹣2,0) ( http: / / www.21cnjy.com ),可得OA=2,再根据含30°的直角三角形的性质可得OB的长,再根据旋转的性质和扇形的面积公式即可求解.
【解答】解:∵点A的坐标(﹣2,0),
∴OA=2,
∵△ABO是直角三角形,∠AOB=60°,
∴∠OAB=30°,
∴OB=OA=1,
∴边OB扫过的面积为:=π.
故答案为:π.
【点评】本题考查了旋转和扇形的面积公式,准确找到运动路径是解题的关键.
练3.【分析】雨刷CD扫过的面积就是一个大扇形﹣小扇形的面积,圆心角是90度,半径分别为115cm,35cm,所以根据扇形的面积公式计算.
【解答】解:由题意可知:△ABD≌△AB′D′,△ACD≌△AC′D′,
且大扇形半径AC=115cm,小扇形半径AD=35cm,且圆心角都为直角,
所以雨刷CD扫过的面积为:
S扇形ACC′﹣S扇形ADD′=﹣=(115+35)(115﹣35)=3000π(cm2).
答:雨刷扫过的面积为3000πcm2.
【点评】此题主要考查了扇形面 ( http: / / www.21cnjy.com )积计算,本题的关键是看出雨刷CD扫过的面积就是一个大扇形﹣小扇形的面积,然后再从一堆的数据中分出哪些是有用的,哪些是没用的.根据扇形的面积公式计算.
课后小测答案:
一、选择题
1.【分析】由∠AOB为90°,得到△ ( http: / / www.21cnjy.com )OAB为等腰直角三角形,于是OA=OB,而S阴影部分=S扇形OAB﹣S△OAB.然后根据扇形和直角三角形的面积公式计算即可.
【解答】解:S阴影部分=S扇形OAB﹣S△OAB
=
=π﹣2
故选:A.
【点评】本题考查了扇形面积的计算,是属 ( http: / / www.21cnjy.com )于基础性的题目的一个组合,只要记住公式即可正确解出.关键是从图中可以看出阴影部分的面积是扇形的面积减去直角三角形的面积.
2.【分析】由正方形的边长为3,可得弧BD的弧长为6,然后利用扇形的面积公式:S扇形DAB=,计算即可.
【解答】解:∵正方形的边长为3,
∴弧BD的弧长=6,
∴S扇形DAB==×6×3=9.
故选:D.
【点评】此题考查了扇形的面积公式,解题的关键是:熟记扇形的面积公式S扇形DAB=.
3.【分析】根据题意得出AB=AB′=12,∠BAB′=60°,根据图形得出图中阴影部分的面积S=+π×122﹣π×122,求出即可.
【解答】解:∵AB=AB′=12,∠BAB′=60°
∴图中阴影部分的面积是:
S=S扇形B′AB+S半圆O′﹣S半圆O
=+π×122﹣π×122
=24π.
故选:B.
( http: / / www.21cnjy.com )
【点评】本题考查的是扇形的面积及旋转的性质,通过做此题培养了学生的计算能力和观察图形的能力,题目比较好,难度适中.
4.【分析】作DM⊥AC于M,DN⊥BC ( http: / / www.21cnjy.com )于N,构造正方形DMCN,利用正方形和等腰直角三角形的性质,通过证明△DMG≌△DNH,把△DHN补到△DNG的位置,得到四边形DGCH的面积=正方形DMCN的面积,于是得到阴影部分的面积=扇形的面积﹣正方形DMCN的面积,即为定值.
【解答】解:作DM⊥AC于M,DN⊥BC于N,连接DC,
( http: / / www.21cnjy.com )
∵CA=CB,∠ACB=90°,
∴∠A=∠B=45°,
DM=AD=AB,DN=BD=AB,
∴DM=DN,
∴四边形DMCN是正方形,
∴∠MDN=90°,
∴∠MDG=90°﹣∠GDN,
∵∠EDF=90°,
∴∠NDH=90°﹣∠GDN,
∴∠MDG=∠NDH,
在△DMG和△DNH中,
,
∴△DMG≌△DNH,
∴四边形DGCH的面积=正方形DMCN的面积,
∵正方形DMCN的面积=DM2=AB2,
∴四边形DGCH的面积=,
∵扇形FDE的面积==,
∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=(定值),
故选:C.
【点评】本题主要考查了等腰直角三角形斜边中线的性质,正方形的性质,全等三角形的判定和性质,能正确作出辅助线构造全等三角形是解题的关键.
二、填空题
5.【分析】将所给数据直接代入扇形面积公式S扇形=进行计算即可得出答案.
【解答】解:由题意得,n=120°,R=6cm,
故=12π.
故答案为12π.
【点评】此题考查了扇形面积的计算,属于基础题,解答本题的关键是熟记扇形的面积公式及公式中字母所表示的含义,难度一般.
6.【分析】利用弧长公式即可求扇形的半径,进而利用扇形的面积公式即可求得扇形的面积.
【解答】解:设扇形的半径为r.
则=6π,
解得r=9,
∴扇形的面积==27π.
故答案为:27π.
【点评】此题主要考查了扇形面积求法,用到的知识点为:扇形的弧长公式l=;扇形的面积公式S=.
7.【分析】由图可知,阴影部分的面积是两个圆心角为90°,且半径为a的扇形的面积与正方形的面积的差,可据此求出阴影部分的面积.
【解答】解:由题意可得出:S阴影=2S扇形﹣S正方形=2×﹣a2=(﹣1)a2.
故答案为:(﹣1)a2.
【点评】本题利用了扇形的面积公式,正方形的面积公式求解,得出S阴影=2S扇形﹣S正方形是解题关键.
8.【分析】连接相交两圆的交点,根据其图形的对称性可知,阴影部分的面积等于公共弦与圆所构成的弓形面积的2倍.
【解答】解:如图连接AB,OA、OB,
( http: / / www.21cnjy.com )
根据对称性可知OA=OB=2,OC⊥AB,OC=1,
∴∠AOB=2∠AOC=2×60°=120°,
∴S阴影部分=2(S扇形AOB﹣S△AOB)
=2()
=(π﹣2)
故答案为:(π﹣2).
【点评】本题考查了扇形的面积及相交两圆的性质,解题的关键是正确的分析图形并分解为两个弓形的面积的和.
9.【分析】阴影部分的面积=2扇形AO1E的面积﹣△AO1O2的面积.
【解答】解:连接AB交O1O2于点C,
( http: / / www.21cnjy.com )
∵把⊙O1向右平移8个单位长度得⊙O2,
∴O1O2=8,
∴O1C=8÷2=4,
易得△AO1O2为等腰直角三角形,
∴AO1=4,
∴阴影部分的面积=2×﹣4×4÷2=8π﹣16,
故答案为8π﹣16.
【点评】本题的难点是得到圆的半径,关键是得到阴影的面积的求法.
10.【分析】过D点作DF⊥AB于点F.可求 ( http: / / www.21cnjy.com ) ABCD和△BCE的高,观察图形可知阴影部分的面积= ABCD的面积﹣扇形ADE的面积﹣△BCE的面积,计算即可求解.
【解答】解:过D点作DF⊥AB于点F.
( http: / / www.21cnjy.com )
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
【点评】考查了平行四边形的性质,扇形面积的计算,本题的关键是理解阴影部分的面积= ABCD的面积﹣扇形ADE的面积﹣△BCE的面积.
11.【分析】首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.
【解答】解:如图所示:连接EFMN,
( http: / / www.21cnjy.com )
∵四边形的边长为2,四个角都是直角,
∴四边形EFMN是正方形,
正方形中两部分阴影面积为:22﹣π×12=4﹣π,
∴正方形内空白面积为:4﹣2(4﹣π)=2π﹣4,
∵⊙O的半径为2,
∴O1,O2,O3,O4的半径为1,
∴小圆的面积为:π×12=π,
扇形COB的面积为:=π,
∴扇形COB中两空白面积相等,
∴阴影部分的面积为:π×22﹣2(2π﹣4)=8.
故答案为:8.
【点评】此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.
12.【分析】由图可知S1=,S2=×3,S3=×5,S4=×7,…Sn=×(2n﹣1),从而得出Sn的值.
【解答】解:由题意可得出通项公式:Sn=×(2n﹣1),
即Sn=×(2n﹣1),
故答案为.
【点评】本题考查了扇形面积的计算,是一道规律性的题目,难度较大.
解答题
13.【考点】扇形面积的计算;弧长的计算;旋转的性质.
【分析】先求出三个扇形的圆心角之和与半径,再根据扇形的面积公式及弧长公式即可得出结论.
【解答】解:∵三个扇形的半径相等,都为1,圆心角之和为135°,
∴三个小扇形的面积和==π,
∴三个小扇形的弧长和==π,
∴三个小扇形的周长和=6+π.
【点评】本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.
14.【分析】直接利用扇形面积公式求出即可.
【解答】解:
阴影部分ABDC的面积=﹣==48π(cm2).
【点评】此题主要考查了扇形面积公式应用,正确记忆扇形面积公式是解题关键.
15.【分析】首先求出∠DOB=60 ( http: / / www.21cnjy.com )°,再利用扇形面积公式求出S扇形DOB,再利用勾股定理求出AD的长,再利用三角形面积公式求出阴影部分面积即可.
【解答】解:过点O作OE⊥AD于点E,连接DO,
( http: / / www.21cnjy.com )
∵∠A=30°,
∴∠DOB=60°,
∴S扇形DOB==π,
∵∠A=30°,AO=4,∴EO=2,∴AE=2,
∴AD=4,
∵∠A=30°,AB=8,
∴BC=×8=,
∴S△ABC=×8×=,
S△AOD=×EO×AD=×2×4=4,
∴阴影部分的面积为:﹣﹣π=﹣.
【点评】此题主要考查了扇形面积公式以及三角形面积公式和勾股定理得出应用,根据已知得出AD的长是解题关键.
16.【分析】根据矩形的性质得到AD=BC=4,∠FAD=90°,根据图形得到S阴=S矩ABCD+S扇ADF﹣S△FBC,然后根据矩形、扇形和三角形的面积公式分别计算得到S矩ABCD=AB BC=8×4=32,S扇ADF==4π,S△FBC=BC FB=×4×(8+4)=24,再代入S阴=S矩ABCD+S扇ADF﹣S△FBC计算即可得到商标图案的面积.
【解答】解:∵矩形ABCD中,AB=2BC,且AB=8cm,
∴AD=BC=4,
∴S阴=S矩ABCD+S扇ADF﹣S△FBC,
∵S矩ABCD=AB BC=8×4=32,
S扇ADF==4π,
S△FBC=BC FB=×4×(8+4)=24,
∴S阴=32+4π﹣24=(8+4π)cm2.
所以商标图案的面积为(8+4π)cm2.
【点评】本题考查了扇形的面积公式:S=(其中n为扇形的圆心角的度数,R为半径).也考查了矩形的性质.
一、学习目标 1.经历探索扇形面积计算公式的过程;2.了解扇形面积计算公式,并会用公式解决问题;3.了解弧长和扇形面积的关系.
二、知识回顾 1.圆的周长2πR可以看作 360 度的圆心角所对的弧(圆的半径为R). 当圆的半径为R时,1°的圆心角所对的弧长是 ;2°的圆心角所对的弧长是 ;60°的圆心角所对的弧长是 ;n°的圆心角所对的弧长是 ;结论:半径为R的圆中,n°的圆心角所对的弧长为.注意:进行计算时,要注意公式中n的意义,n表示1°的圆心角的倍数,它是不带单位的.
三、新知讲解 1.扇形由 组成圆心角的两条半径和圆心角所对的弧 所围成的图形叫做扇形.2.扇形的面积在半径为R的圆中,因为360°的圆心角所对的扇形面积就是圆的面积S=πR2,所以圆心角是1°的扇形面积是 .于是,圆心角为n°的扇形面积是 .因为n°的圆心角所对的弧长为,所以=.3.阴影部分面积的四种求法(1)公式法:当已知图形为我们熟知的基本图形或将图形分割成几个可直接利用公式求面积的图形时,我们可直接利用有关面积公式求解.(2)等积变换法:把所求阴影部分的图形适当进行等积变形,即找出与它面积相等的特殊图形,从而求出阴影部分图形的面积.(3)整体法:当阴影部分图形为分散的个体时,可针对其结构特征,视各阴影部分图形为一个整体,然后利用相关图形的面积公式整体求出.(4)割补法:将一个图形的一部分割下来,移动到其他合适的位置上,从而构成易求面积的图形.
四、典例探究 扫一扫,有惊喜哦!1.求扇形面积【例1】(2015 湖州)如图,已知C, ( http: / / www.21cnjy.com )D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______. ( http: / / www.21cnjy.com )总结:利用扇形的面积公式进行求解注意两种情况:(1)已知圆心角和半径,利用公式;(2)已知弧长和半径,利用公式.练1.(2013四川凉山州)如图,在Rt△ ( http: / / www.21cnjy.com )ABC中,∠C=90°,AC=8,BC=6,两等⊙A、⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为 . ( http: / / www.21cnjy.com )2.求弓形面积【例2】如图,AB为⊙O的切线,切点为B, ( http: / / www.21cnjy.com )连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( ) ( http: / / www.21cnjy.com )A. B. C. D.总结:求弓形的面积一般是转化为求扇形面积与三角形面积的差.求弓形面积时,一般要用到垂径定理,所以过圆心作弦的垂线段是常见的辅助线.练2.(2015 福州校级质检)如图,AB为⊙O的直径,弦AC=2,∠B=30°,∠ACB的平分线交⊙O于点D,求:(1)BC、AD的长;(2)图中两阴影部分面积的和. ( http: / / www.21cnjy.com )3.求图形绕某点旋转后扫过的面积【例3】(2015 永州) ( http: / / www.21cnjy.com )如图,在平面直角坐标系中,点A的坐标(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为_____. ( http: / / www.21cnjy.com )总结:求图形绕某点旋转后扫过的图形面积 ( http: / / www.21cnjy.com ),先要根据运动轨迹分析出扫过的图形的形状,然后根据图形形状求解面积.如果是规则图形,就利用规则图形的公式进行计算;如果是不规则图形,要先转化为规则图形.不规则图形转化为规则图形的方法有:等积变换法.对所求图形进行适当等积变形,即找到与它面积相等的规则图形;割补法.对所求图形进行适当分割,并将一部分图形移位,组成规则图形;.练3.(2012 广东校级模拟)当 ( http: / / www.21cnjy.com )汽车在雨天行驶时,司机为了看清楚道路,要启动前方挡风玻璃上的雨刷器.如图是某汽车的一个雨刷器的转动示意图,雨刷器杆AB与雨刷CD在B处固定连接(不能转动),当杆AB绕A点转动90°时,雨刷CD扫过的面积如图所示,现量得:CD=80cm、∠DBA=20°,AC=115cm,DA=35cm,试从以上信息中选择所需要的数据,求出雨刷扫过的面积. ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.(2015 甘孜州)如图,已知扇形AOB的半径为2,圆心角为90°,连接AB,则图中阴影部分的面积是( ) ( http: / / www.21cnjy.com )A.π﹣2 B.π﹣4 C.4π﹣2 D.4π﹣42.(2015 东莞)如图,某数学 ( http: / / www.21cnjy.com )兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( ) ( http: / / www.21cnjy.com )A.6 B.7 C.8 D.93.(2015 达州)如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( ) ( http: / / www.21cnjy.com )A.12π B.24π C.6π D.36π4.(2015 咸宁)如图,在△ABC中,C ( http: / / www.21cnjy.com )A=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( ) ( http: / / www.21cnjy.com )A.由小到大 B.由大到小C.不变 D.先由小到大,后由大到小二、填空题5.(2015 泰州)圆心角为120°,半径长为6cm的扇形面积是______cm2.6.(2015 常州)已知扇形的圆心角为120°,弧长为6π,则扇形的面积是________.7.(2014 洛阳二模) ( http: / / www.21cnjy.com )如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为__________. ( http: / / www.21cnjy.com )8.(2011 高淳县一 ( http: / / www.21cnjy.com )模)如图,两个半径为2cm的等圆互相重叠,且各自的圆心都在另一个圆上,则两圆重叠部分的面积是_______cm2.(结果保留π). ( http: / / www.21cnjy.com )9.(2012 黄陂区校级模拟)如图, ( http: / / www.21cnjy.com )把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A、B,且O1A⊥O2A,则图中阴影部分的面积是________. ( http: / / www.21cnjy.com )10.(2015 安顺)如图,在 AB ( http: / / www.21cnjy.com )CD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是_________(结果保留π). ( http: / / www.21cnjy.com )11.(2015 江阴市校级一模) ( http: / / www.21cnjy.com )如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA,OB,OC,OD的中点,若⊙O的半径为2,则阴影部分的面积为__________. ( http: / / www.21cnjy.com )12.(2015 东莞模拟)如图是圆心角 ( http: / / www.21cnjy.com )为30°,半径分别是1、3、5、7、…的扇形组成的图形,阴影部分的面积依次记为S1、S2、S3、…,则Sn=_________.(结果保留π) ( http: / / www.21cnjy.com )三、解答题13.(2013 路南区一模)如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π). ( http: / / www.21cnjy.com )14.(2013秋 章丘市校级期末)如图,两个同心圆的半径分别为18cm和30cm,又知∠COD=30°,求阴影部分ABDC的面积. ( http: / / www.21cnjy.com )15.(2013秋 海门市校级期中) ( http: / / www.21cnjy.com )如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积. ( http: / / www.21cnjy.com )16.(2012 云和县模拟)一个商标 ( http: / / www.21cnjy.com )图案如图,矩形ABCD中,AB=2BC,且AB=8cm,以A为圆心,AD长为半径作半圆,求商标图案的面积. ( http: / / www.21cnjy.com )
典例探究答案:
【例1】【分析】图中阴影部分的面积=半圆的面积﹣圆心角是120°的扇形的面积,根据扇形面积的计算公式计算即可求解.
【解答】解:图中阴影部分的面积=π×22﹣=2π﹣π=π.
答:图中阴影部分的面积等于π.
故答案为:π.
【点评】考查了扇形面积的计算,求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.
练1.解:
【例2】【分析】过O点作OE⊥ ( http: / / www.21cnjy.com )CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积﹣三角形OCD的面积,列式计算即可求解.
【解答】解:过O点作OE⊥CD于E,
( http: / / www.21cnjy.com )
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=,
∴CD=2,
∴图中阴影部分的面积为:﹣×2×1=π﹣.
故选:A.
【点评】本题考查了扇形面积的计算,切线的性质,解题的关键是理解阴影部分的面积=扇形OCD的面积﹣三角形OCD的面积.
练2.【分析】(1)根据直径得出∠ACB=∠ADB=90°,根据勾股定理求出BC,根据圆周角定理求出AD=BD,求出AD即可;
(2)根据三角形的面积公式,求出△AOC和△AOD的面积,再求出S扇形COD,即可求出答案.
【解答】解:(1)∵AB是直径,
∴∠ACB=∠ADB=90°(直径所对的圆周角是直角),
在Rt△ABC中,∠B=30°,AC=2,
∴AB=4,
∴BC==2,
∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD
∴=,
∴AD=BD,
∴在Rt△ABD中,AD=BD=AB=2;
(2)连接OC,OD,
( http: / / www.21cnjy.com )
∵∠B=30°,
∴∠AOC=∠2∠B=60°,
∵OA=OB,
∴S△AOC=S△ABC=××AC×BC=××2×2=,
由(1)得∠AOD=90°,
∴∠COD=150°,
S△AOD=×AO×OD=×22=2,
∴S阴影=S扇形COD﹣S△AOC﹣S△AOD=﹣﹣2=π﹣﹣2.
【点评】本题考查了勾股定理、圆周角定理 ( http: / / www.21cnjy.com )、三角形的面积等知识点的应用,关键是求出∠ACB=∠ADB=90°,题型较好,通过做此题,培养了学生运用定理进行推理的能力.
【例3】【分析】根据点A的坐标(﹣2,0) ( http: / / www.21cnjy.com ),可得OA=2,再根据含30°的直角三角形的性质可得OB的长,再根据旋转的性质和扇形的面积公式即可求解.
【解答】解:∵点A的坐标(﹣2,0),
∴OA=2,
∵△ABO是直角三角形,∠AOB=60°,
∴∠OAB=30°,
∴OB=OA=1,
∴边OB扫过的面积为:=π.
故答案为:π.
【点评】本题考查了旋转和扇形的面积公式,准确找到运动路径是解题的关键.
练3.【分析】雨刷CD扫过的面积就是一个大扇形﹣小扇形的面积,圆心角是90度,半径分别为115cm,35cm,所以根据扇形的面积公式计算.
【解答】解:由题意可知:△ABD≌△AB′D′,△ACD≌△AC′D′,
且大扇形半径AC=115cm,小扇形半径AD=35cm,且圆心角都为直角,
所以雨刷CD扫过的面积为:
S扇形ACC′﹣S扇形ADD′=﹣=(115+35)(115﹣35)=3000π(cm2).
答:雨刷扫过的面积为3000πcm2.
【点评】此题主要考查了扇形面 ( http: / / www.21cnjy.com )积计算,本题的关键是看出雨刷CD扫过的面积就是一个大扇形﹣小扇形的面积,然后再从一堆的数据中分出哪些是有用的,哪些是没用的.根据扇形的面积公式计算.
课后小测答案:
一、选择题
1.【分析】由∠AOB为90°,得到△ ( http: / / www.21cnjy.com )OAB为等腰直角三角形,于是OA=OB,而S阴影部分=S扇形OAB﹣S△OAB.然后根据扇形和直角三角形的面积公式计算即可.
【解答】解:S阴影部分=S扇形OAB﹣S△OAB
=
=π﹣2
故选:A.
【点评】本题考查了扇形面积的计算,是属 ( http: / / www.21cnjy.com )于基础性的题目的一个组合,只要记住公式即可正确解出.关键是从图中可以看出阴影部分的面积是扇形的面积减去直角三角形的面积.
2.【分析】由正方形的边长为3,可得弧BD的弧长为6,然后利用扇形的面积公式:S扇形DAB=,计算即可.
【解答】解:∵正方形的边长为3,
∴弧BD的弧长=6,
∴S扇形DAB==×6×3=9.
故选:D.
【点评】此题考查了扇形的面积公式,解题的关键是:熟记扇形的面积公式S扇形DAB=.
3.【分析】根据题意得出AB=AB′=12,∠BAB′=60°,根据图形得出图中阴影部分的面积S=+π×122﹣π×122,求出即可.
【解答】解:∵AB=AB′=12,∠BAB′=60°
∴图中阴影部分的面积是:
S=S扇形B′AB+S半圆O′﹣S半圆O
=+π×122﹣π×122
=24π.
故选:B.
( http: / / www.21cnjy.com )
【点评】本题考查的是扇形的面积及旋转的性质,通过做此题培养了学生的计算能力和观察图形的能力,题目比较好,难度适中.
4.【分析】作DM⊥AC于M,DN⊥BC ( http: / / www.21cnjy.com )于N,构造正方形DMCN,利用正方形和等腰直角三角形的性质,通过证明△DMG≌△DNH,把△DHN补到△DNG的位置,得到四边形DGCH的面积=正方形DMCN的面积,于是得到阴影部分的面积=扇形的面积﹣正方形DMCN的面积,即为定值.
【解答】解:作DM⊥AC于M,DN⊥BC于N,连接DC,
( http: / / www.21cnjy.com )
∵CA=CB,∠ACB=90°,
∴∠A=∠B=45°,
DM=AD=AB,DN=BD=AB,
∴DM=DN,
∴四边形DMCN是正方形,
∴∠MDN=90°,
∴∠MDG=90°﹣∠GDN,
∵∠EDF=90°,
∴∠NDH=90°﹣∠GDN,
∴∠MDG=∠NDH,
在△DMG和△DNH中,
,
∴△DMG≌△DNH,
∴四边形DGCH的面积=正方形DMCN的面积,
∵正方形DMCN的面积=DM2=AB2,
∴四边形DGCH的面积=,
∵扇形FDE的面积==,
∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=(定值),
故选:C.
【点评】本题主要考查了等腰直角三角形斜边中线的性质,正方形的性质,全等三角形的判定和性质,能正确作出辅助线构造全等三角形是解题的关键.
二、填空题
5.【分析】将所给数据直接代入扇形面积公式S扇形=进行计算即可得出答案.
【解答】解:由题意得,n=120°,R=6cm,
故=12π.
故答案为12π.
【点评】此题考查了扇形面积的计算,属于基础题,解答本题的关键是熟记扇形的面积公式及公式中字母所表示的含义,难度一般.
6.【分析】利用弧长公式即可求扇形的半径,进而利用扇形的面积公式即可求得扇形的面积.
【解答】解:设扇形的半径为r.
则=6π,
解得r=9,
∴扇形的面积==27π.
故答案为:27π.
【点评】此题主要考查了扇形面积求法,用到的知识点为:扇形的弧长公式l=;扇形的面积公式S=.
7.【分析】由图可知,阴影部分的面积是两个圆心角为90°,且半径为a的扇形的面积与正方形的面积的差,可据此求出阴影部分的面积.
【解答】解:由题意可得出:S阴影=2S扇形﹣S正方形=2×﹣a2=(﹣1)a2.
故答案为:(﹣1)a2.
【点评】本题利用了扇形的面积公式,正方形的面积公式求解,得出S阴影=2S扇形﹣S正方形是解题关键.
8.【分析】连接相交两圆的交点,根据其图形的对称性可知,阴影部分的面积等于公共弦与圆所构成的弓形面积的2倍.
【解答】解:如图连接AB,OA、OB,
( http: / / www.21cnjy.com )
根据对称性可知OA=OB=2,OC⊥AB,OC=1,
∴∠AOB=2∠AOC=2×60°=120°,
∴S阴影部分=2(S扇形AOB﹣S△AOB)
=2()
=(π﹣2)
故答案为:(π﹣2).
【点评】本题考查了扇形的面积及相交两圆的性质,解题的关键是正确的分析图形并分解为两个弓形的面积的和.
9.【分析】阴影部分的面积=2扇形AO1E的面积﹣△AO1O2的面积.
【解答】解:连接AB交O1O2于点C,
( http: / / www.21cnjy.com )
∵把⊙O1向右平移8个单位长度得⊙O2,
∴O1O2=8,
∴O1C=8÷2=4,
易得△AO1O2为等腰直角三角形,
∴AO1=4,
∴阴影部分的面积=2×﹣4×4÷2=8π﹣16,
故答案为8π﹣16.
【点评】本题的难点是得到圆的半径,关键是得到阴影的面积的求法.
10.【分析】过D点作DF⊥AB于点F.可求 ( http: / / www.21cnjy.com ) ABCD和△BCE的高,观察图形可知阴影部分的面积= ABCD的面积﹣扇形ADE的面积﹣△BCE的面积,计算即可求解.
【解答】解:过D点作DF⊥AB于点F.
( http: / / www.21cnjy.com )
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
【点评】考查了平行四边形的性质,扇形面积的计算,本题的关键是理解阴影部分的面积= ABCD的面积﹣扇形ADE的面积﹣△BCE的面积.
11.【分析】首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.
【解答】解:如图所示:连接EFMN,
( http: / / www.21cnjy.com )
∵四边形的边长为2,四个角都是直角,
∴四边形EFMN是正方形,
正方形中两部分阴影面积为:22﹣π×12=4﹣π,
∴正方形内空白面积为:4﹣2(4﹣π)=2π﹣4,
∵⊙O的半径为2,
∴O1,O2,O3,O4的半径为1,
∴小圆的面积为:π×12=π,
扇形COB的面积为:=π,
∴扇形COB中两空白面积相等,
∴阴影部分的面积为:π×22﹣2(2π﹣4)=8.
故答案为:8.
【点评】此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.
12.【分析】由图可知S1=,S2=×3,S3=×5,S4=×7,…Sn=×(2n﹣1),从而得出Sn的值.
【解答】解:由题意可得出通项公式:Sn=×(2n﹣1),
即Sn=×(2n﹣1),
故答案为.
【点评】本题考查了扇形面积的计算,是一道规律性的题目,难度较大.
解答题
13.【考点】扇形面积的计算;弧长的计算;旋转的性质.
【分析】先求出三个扇形的圆心角之和与半径,再根据扇形的面积公式及弧长公式即可得出结论.
【解答】解:∵三个扇形的半径相等,都为1,圆心角之和为135°,
∴三个小扇形的面积和==π,
∴三个小扇形的弧长和==π,
∴三个小扇形的周长和=6+π.
【点评】本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.
14.【分析】直接利用扇形面积公式求出即可.
【解答】解:
阴影部分ABDC的面积=﹣==48π(cm2).
【点评】此题主要考查了扇形面积公式应用,正确记忆扇形面积公式是解题关键.
15.【分析】首先求出∠DOB=60 ( http: / / www.21cnjy.com )°,再利用扇形面积公式求出S扇形DOB,再利用勾股定理求出AD的长,再利用三角形面积公式求出阴影部分面积即可.
【解答】解:过点O作OE⊥AD于点E,连接DO,
( http: / / www.21cnjy.com )
∵∠A=30°,
∴∠DOB=60°,
∴S扇形DOB==π,
∵∠A=30°,AO=4,∴EO=2,∴AE=2,
∴AD=4,
∵∠A=30°,AB=8,
∴BC=×8=,
∴S△ABC=×8×=,
S△AOD=×EO×AD=×2×4=4,
∴阴影部分的面积为:﹣﹣π=﹣.
【点评】此题主要考查了扇形面积公式以及三角形面积公式和勾股定理得出应用,根据已知得出AD的长是解题关键.
16.【分析】根据矩形的性质得到AD=BC=4,∠FAD=90°,根据图形得到S阴=S矩ABCD+S扇ADF﹣S△FBC,然后根据矩形、扇形和三角形的面积公式分别计算得到S矩ABCD=AB BC=8×4=32,S扇ADF==4π,S△FBC=BC FB=×4×(8+4)=24,再代入S阴=S矩ABCD+S扇ADF﹣S△FBC计算即可得到商标图案的面积.
【解答】解:∵矩形ABCD中,AB=2BC,且AB=8cm,
∴AD=BC=4,
∴S阴=S矩ABCD+S扇ADF﹣S△FBC,
∵S矩ABCD=AB BC=8×4=32,
S扇ADF==4π,
S△FBC=BC FB=×4×(8+4)=24,
∴S阴=32+4π﹣24=(8+4π)cm2.
所以商标图案的面积为(8+4π)cm2.
【点评】本题考查了扇形的面积公式:S=(其中n为扇形的圆心角的度数,R为半径).也考查了矩形的性质.
同课章节目录
