【多媒体导学案】人教版数学九年级上册第24章第15课时《圆锥侧面上最短路径问题》(教师版)
文档属性
| 名称 | 【多媒体导学案】人教版数学九年级上册第24章第15课时《圆锥侧面上最短路径问题》(教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-30 11:25:40 | ||
图片预览



文档简介
一、学习目标 1.复习和巩固圆锥的侧面和侧面展开图之间的关系;2.掌握圆锥侧面上路径最短问题的解决方案.3.对最短距离问题或最短路径问题进行归纳,培养学生解决此类问题的能力.
二、知识回顾 1.圆锥的侧面展开图圆锥的母线------扇形的 半径 圆锥的底面周长------扇形的 弧长 ( http: / / www.21cnjy.com )侧面展开得到的扇形的圆心角为 2. 平面上,两点之间,线段最短.
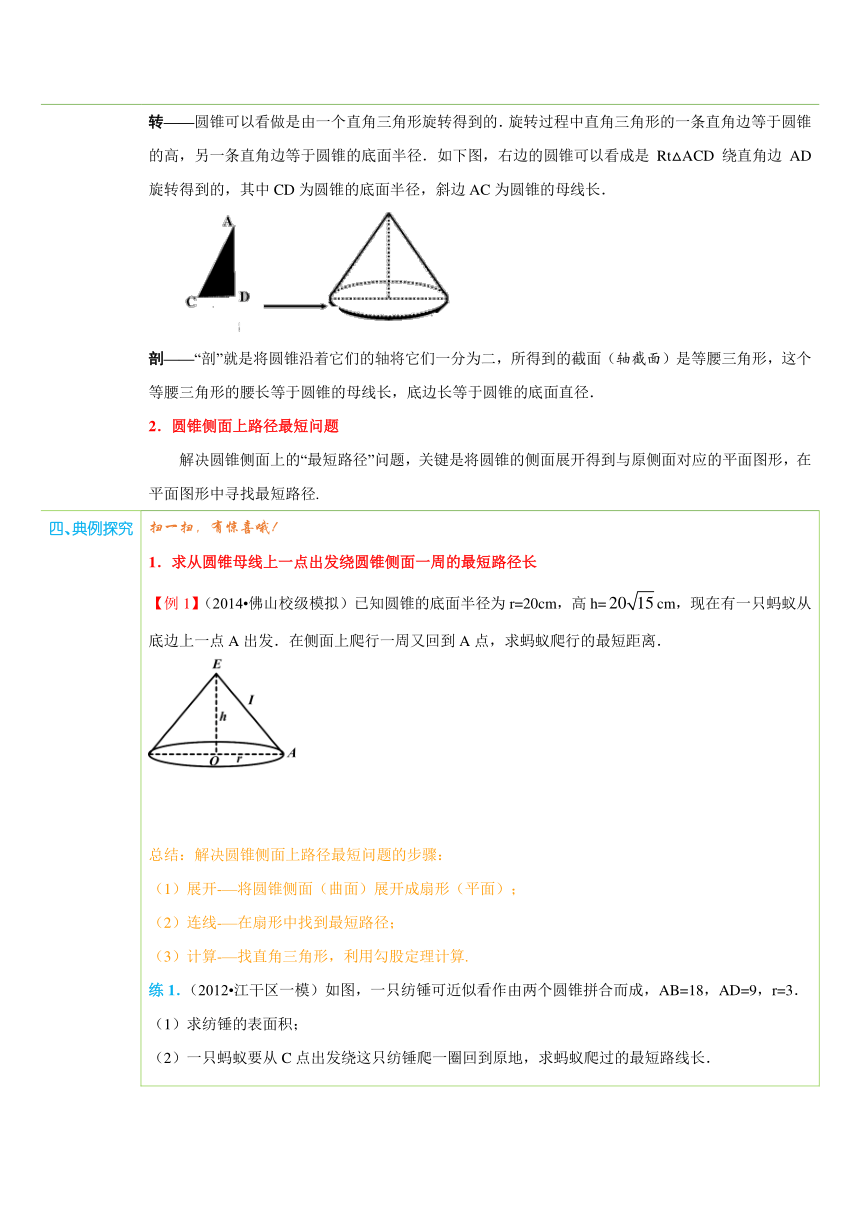
三、新知讲解 1. 圆锥中的展、围、转、剖圆锥是一种重要的几何体,与它相关的计算类型繁多,若能根据展、围、转、剖的特征学习圆锥,则这部分知识可迎刃而解.请看下面的解读.展——“展”就是把一个圆锥的侧面沿它的一 ( http: / / www.21cnjy.com )条母线剪开后展在一个平面上.圆锥的侧面展开图是一个扇形,此时圆锥的底面周长等于扇形的弧长,圆锥的母线长等于扇形的半径.围——“围”就是将扇形两边的半径拼到一起,围成一个圆锥,它与“展”恰好相反.此时,扇形的圆心就成了圆锥的顶点,扇形的半径就变成了圆锥的母线,扇形的弧长变成了圆锥底面圆的周长.下图是圆锥和圆锥的侧面展开图,体现了圆锥和扇形之间的转化关系,灵活理解“展”和“围”的过程,可以帮助同学们理解圆锥的侧面积和全面积的计算公式:S圆锥侧=S扇形=·2πr·l=πrl,S圆锥全=πrl+πr2. ( http: / / www.21cnjy.com )转——圆锥可以看做是由一个直角三角形旋转得 ( http: / / www.21cnjy.com )到的.旋转过程中直角三角形的一条直角边等于圆锥的高,另一条直角边等于圆锥的底面半径.如下图,右边的圆锥可以看成是Rt△ACD绕直角边AD旋转得到的,其中CD为圆锥的底面半径,斜边AC为圆锥的母线长. ( http: / / www.21cnjy.com )剖——“剖”就是将圆锥沿着它们的轴将它们一 ( http: / / www.21cnjy.com )分为二,所得到的截面(轴截面)是等腰三角形,这个等腰三角形的腰长等于圆锥的母线长,底边长等于圆锥的底面直径.2.圆锥侧面上路径最短问题解决圆锥侧面上的“最短路径”问题,关键是将圆锥的侧面展开得到与原侧面对应的平面图形,在平面图形中寻找最短路径.
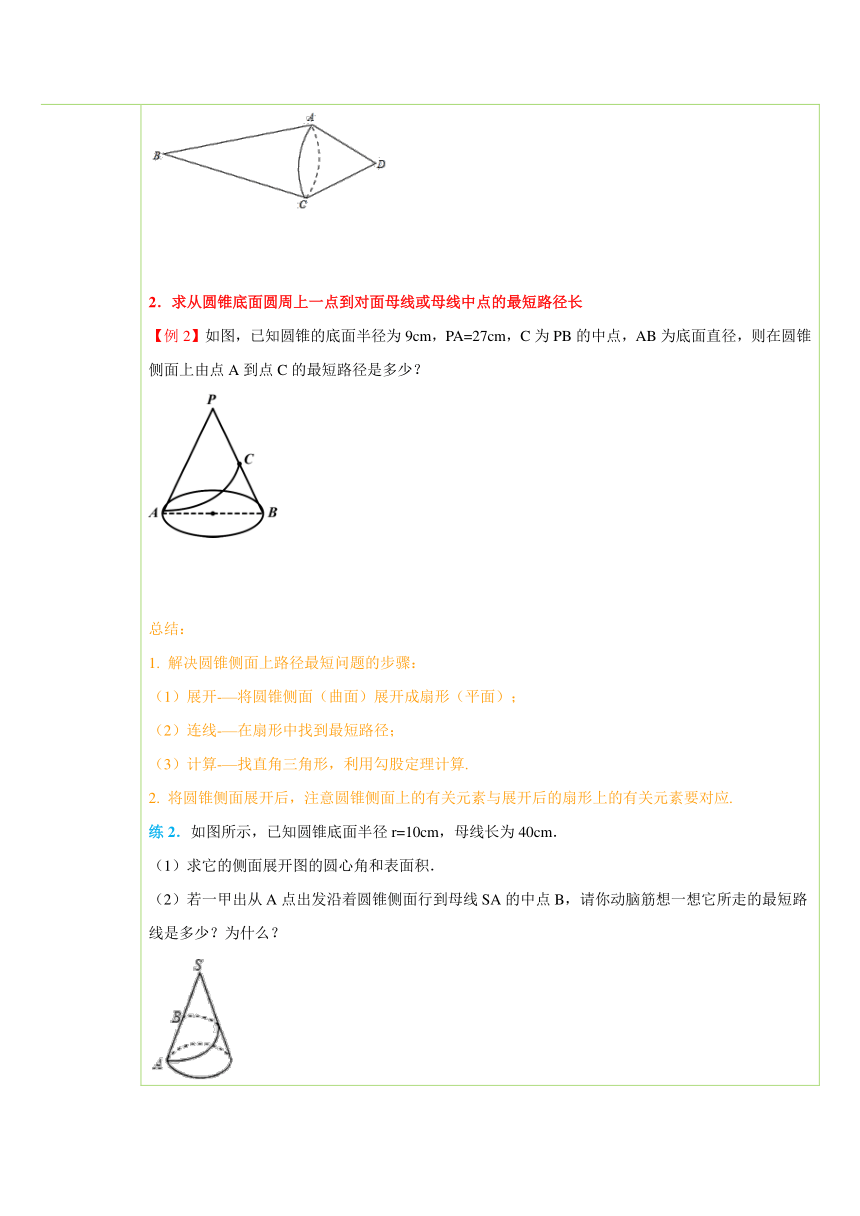
四、典例探究 扫一扫,有惊喜哦!1.求从圆锥母线上一点出发绕圆锥侧面一周的最短路径长【例1】(2014 佛山校级模拟)已知圆锥的底面半径为r=20cm,高h=cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离. ( http: / / www.21cnjy.com )总结:解决圆锥侧面上路径最短问题的步骤:(1)展开-—将圆锥侧面(曲面)展开成扇形(平面);(2)连线-—在扇形中找到最短路径;(3)计算-—找直角三角形,利用勾股定理计算.练1.(2012 江干区一模)如图,一只纺锤可近似看作由两个圆锥拼合而成,AB=18,AD=9,r=3.(1)求纺锤的表面积;(2)一只蚂蚁要从C点出发绕这只纺锤爬一圈回到原地,求蚂蚁爬过的最短路线长. ( http: / / www.21cnjy.com )2.求从圆锥底面圆周上一点到对面母线或母线中点的最短路径长【例2】如图,已知圆锥的底面半径为9cm,PA=27cm,C为PB的中点,AB为底面直径,则在圆锥侧面上由点A到点C的最短路径是多少? ( http: / / www.21cnjy.com )总结:1. 解决圆锥侧面上路径最短问题的步骤:(1)展开-—将圆锥侧面(曲面)展开成扇形(平面);(2)连线-—在扇形中找到最短路径;(3)计算-—找直角三角形,利用勾股定理计算.2. 将圆锥侧面展开后,注意圆锥侧面上的有关元素与展开后的扇形上的有关元素要对应.练2.如图所示,已知圆锥底面半径r=10cm,母线长为40cm.(1)求它的侧面展开图的圆心角和表面积.(2)若一甲出从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么? ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.如图,已知圆锥的母线长OA=6,底面圆的半径为2,一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处.则小虫所走的最短距离为( ) ( http: / / www.21cnjy.com )A.12 B.4π C. D.2.(2015 虎林市校级 ( http: / / www.21cnjy.com )二模)一圆锥体形状的圣诞帽,母线长是30cm,底面圆的直径是15cm,点A为圆锥底面圆周上一点,从A点开始绕圆锥侧面缠一圈彩带回到A点,则彩带最少用( )厘米(接口处重合部分忽略不计)A.30πcm B.30cm C.15πcm D.15cm3.(2014 新泰市一模)如图,圆锥 ( http: / / www.21cnjy.com )的轴截面△ABC是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径BC=4cm,母线AB=6cm,则由点B出发,经过圆锥的侧面到达母线AC的最短路程是( ) ( http: / / www.21cnjy.com )A.cm B.6cm C.cm D.4cm二、填空题4.(2014 番禺区校级二模)圆 ( http: / / www.21cnjy.com )锥的底面半径是1,母线长是4,一只蜘蛛从底面圆周上的一点A出发沿圆锥的侧面爬行一周后回到A点,则蜘蛛爬行的最短路径的长是_________.三、解答题5.(2012秋 杭州期末)如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度. ( http: / / www.21cnjy.com )6.(2011秋 宁海县期中)圆锥 ( http: / / www.21cnjy.com )的底面半径是3,母线长是9,P是底面圆周上一点:从点P拉一根绳子绕圆锥侧面一周,再回到P点,求这根绳子的最短长度. ( http: / / www.21cnjy.com )7.(2010 桥西区模拟)如图,圆锥底面的半径为10cm,高为10cm.(1)求圆锥的全面积;(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离. ( http: / / www.21cnjy.com )8.(2010 巫山县模拟)如图,有一堆圆锥形的稻谷,垂直高度CO=m,底面⊙O的直径AB=4m,B处有一小猫想去捕捉母线AC中点D处的老鼠,求出小猫绕侧面前行的最短距离. ( http: / / www.21cnjy.com )9.(2011 张家口模拟)动手操作: ( http: / / www.21cnjy.com )如图①,把长为l、宽为h的矩形卷成以AB为高的圆柱形,则点A′与点A重合,点B′与点B重合;探究发现:如图②,圆柱的底面周长是40,高是30,若在 ( http: / / www.21cnjy.com )圆柱体的侧面绕一圈丝线作装饰,从下底面A出发,沿圆柱侧面绕一周到上底面B,则这条丝线最短的长度是50;实践与应用:如图③,圆锥的母线长为4,底面半径为,若在圆锥体的侧面绕一圈彩带做装饰,从圆锥的底面上的点A出发,沿圆锥侧面绕一周回到点A.求这条彩带最短的长度是多少?拓展联想:如图④,一颗古树上下粗细相 ( http: / / www.21cnjy.com )差不大,可以看成圆柱体.测得树干的周长为3米,高为18米,有一根紫藤自树底部均匀的盘绕在树干上,恰好绕8周到达树干的顶部,你能求出这条紫藤至少有多少米吗?
典例探究答案:
【例1】【分析】蚂蚁爬行 ( http: / / www.21cnjy.com )的最短距离是圆锥的展开图的扇形中AA′的长度.根据勾股定理求得母线长后,利用弧长等于底面周长求得扇形的圆心角的度数为90度,再由等腰直角三角形的性质求解.
【解答】解:设扇形的圆心角为n°,圆锥的顶为E,
( http: / / www.21cnjy.com )
∵r=20cm,h=cm
∴由勾股定理可得母线l==80cm,
而圆锥侧面展开后的扇形的弧长为2×20π=,
∴n=90
即△EAA′是等腰直角三角形,
∴由勾股定理得:AA'==80cm.
答:蚂蚁爬行的最短距离为80cm.
【点评】本题利用了勾股定理,弧长公式,圆的周长公式,等腰直角三角形的性质求解.
练1.【分析】(1)分别计算两个圆锥的侧面积后相加即可得到结果.
(2)首先求得展开扇形的圆心角的度数,然后分两种情况得到两种结果即可比较出最短线路的长.
【解答】解:(1)S=S1+S2=27π+54π=81π;(3分)
(2)∵,∴==120°,
连接CC′,过点D作CC′的垂线,垂足为E,
( http: / / www.21cnjy.com )
则由垂径定理可知CE=C′E,在直角三角形DEC中,∠CDE=30°,CD=9,
由勾股定理,可得:CE=,
∴CC′=2CE=2×9×=9.
如经左边,同理可得另一最短路线为18.
∵9<9×=9×2=18,
∴蚂蚁爬过的最短路线长为9.
【点评】本题考查了圆锥的计算,解题的关键是熟知圆锥的有关元素与扇形的有关元素的对应.
【例2】【分析】最短距离的问题首先应转 ( http: / / www.21cnjy.com )化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.
【解答】解:如图所示,
( http: / / www.21cnjy.com )
∴设圆心角为n°,则=2π×9,解得n=120.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90°.
∴∠CAP=30°,在△RtAPC中,利用勾股定理可得:
∴AC=.
答:由点A到点C的最短路径长是.
【点评】本题考查了圆锥的计算,需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.
练2.【分析】(1)利用圆锥的弧长等于 ( http: / / www.21cnjy.com )底面周长得到圆锥的侧面展开图的圆心角;圆锥表面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长;
(2)最短路线应放在平面内,构造直角三角形,求两点之间的线段的长度.
【解答】解:(1)=2π×10,
解得n=90.
圆锥表面积=π×102+π×10×40=500πcm2.
(2)如右图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
( http: / / www.21cnjy.com )
在Rt△ASB中,SA=40,SB=20,
∴AB=20(cm).
∴甲虫走的最短路线的长度是20cm.
【点评】用到的知识点为:圆锥的弧长 ( http: / / www.21cnjy.com )等于底面周长;求立体图形中两点之间的最短路线长,一般应放在平面内,构造直角三角形,求两点之间的线段的长度.
课后小测答案:
一、选择题
1.【分析】利用圆锥的底面周长等于侧面展开图的弧长可得圆锥侧面展开图的圆心角,求出侧面展开图中两点间的距离即为最短距离.
【解答】解:∵底面圆的半径为2,
∴圆锥的底面周长为2π×2=4π,
设圆锥的侧面展开图的圆心角为n.
∴=4π,
解得n=120°,
作OC⊥AA′于点C,
( http: / / www.21cnjy.com )
∴∠AOC=60°,
∴AC=OA×sin60°=3,
∴AA′=2AC=6.
故选D.
【点评】考查圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.
2.【分析】画出圆锥展开图,设扇形的圆心角∠ASA′=n°,根据弧长公式得到=2 π 15,解得n=90,则可判断△SAA′为等腰直角三角形,然后根据等腰直角三角形的性质求解.
【解答】解:如图,设扇形的圆心角∠ASA′=n°,
( http: / / www.21cnjy.com )
根据题意得=2 π 15,解得n=90,
所以△SAA′为等腰直角三角形,
所以AA′=SA=30,
即彩带最少用30厘米.
故选B.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
3.【分析】沿母线AB把圆锥展开,过B作 ( http: / / www.21cnjy.com )BD⊥AC′于D,根据两点之间线段最短,得到由点B出发,经过圆锥的侧面到达母线AC的最短路程为BD,BC′弧长为圆锥底面圆的周长的一半,再根据弧长公式计算出∠DAB,最后解Rt△ADB,即可得到BD.
【解答】解:沿母线AB把圆锥展开,如图,
过B作BD⊥AC′于D,
( http: / / www.21cnjy.com )
弧BC′= 2π 2=2π,
设∠C′AB=n°,
∴2π=,
∴n=60,即∠DAB=60°,
在Rt△ADB中,AD=AB=×6=3,
∴BD=AD=3,
所以由点B出发,经过圆锥的侧面到达母线AC的最短路程为3cm.
故选C.
【点评】本题考查了圆锥的展开图的有关 ( http: / / www.21cnjy.com )计算:展开图为扇形,弧长为圆锥底面圆的周长,半径为圆锥的母线长.也考查了把立体图形中的问题转化为平面图形来解决.
二、填空题
4.【分析】利用圆锥侧面展开图的弧长等于底面圆的周长,进而得出扇形圆心角的度数,再利用勾股定理求出AA′的长.
【解答】解:由题意可得出:OA=OA′=4,
( http: / / www.21cnjy.com )
==2π,
解得:n=90°,
∴∠AOA′=90°,
∴AA′==4,
故答案为:4.
【点评】此题主要考查了平面展开图的最短路径问题,得出∠AOA′的度数是解题关键.
三、解答题
5.【分析】(1)根据勾股定理直接求出圆锥的高,再利用圆锥侧面展开图弧长与其底面周长的长度关系,求出侧面展开图中∠ABC的度数即可;
(2)首先求出BD的长,再利用勾股定理求出AD以及AC的长即可.
【解答】解:(1)圆锥的高=,
底面圆的周长等于:2π×2=,
解得:n=120°;
(2)连结AC,过B作BD⊥AC于D,则∠ABD=60°.
( http: / / www.21cnjy.com )
由AB=6,可求得BD=3,
∴AD═,
AC=2AD=,
即这根绳子的最短长度是.
【点评】此题考查了圆锥的计算;得到圆锥的底面圆的周长和扇形弧长相等是解决本题的突破点.
6.【分析】圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对直径,转化为求直径的长的问题.
【解答】解:将圆锥侧面沿AB剪开展平,连BB′,则BB′就是所求绳子长.
( http: / / www.21cnjy.com )
由2π×3=得n=120,
作AC⊥BB',则∠2=60°BB'=2BC,
∴∠3=30°∴AC=,BC=,
∴BB′=.
【点评】本题主要考查圆锥的计算,圆锥的 ( http: / / www.21cnjy.com )侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
7.【分析】(1)首先求得圆锥的母线长,然后求得展开扇形的弧长,进而求得其侧面积和底面积,从而求得其全面积;
(2)将圆锥的侧面展开,求得其展开扇形的圆心角的度数是90°,利用勾股定理求得AM的长即为最短距离.
【解答】解:(1)由题意,可得圆锥的母线SA==40(cm)
圆锥的侧面展开扇形的弧长l=2π OA=20πcm
∴S侧=L SA=400πcm2
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(400+100)π=500π(cm2);
(2)沿母线SA将圆锥的侧面展开,如图,则线段AM的长就是蚂蚁所走的最短距离
( http: / / www.21cnjy.com )
由(1)知,SA=40cm,弧AA′=20πcm
∵=20πcm,
∴∠S=n==90°,
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
【点评】本题利用了勾股定理,弧长公式,圆的周长公式,等直角三角形的性质求解.
8.【分析】求这只小猫经过的最 ( http: / / www.21cnjy.com )短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为6cm的等边三角形可知,展开图是半径是6的半圆.点B是半圆的一个端点,而点P是平分半圆的半径的中点,根据勾股定理就可求出两点B和P在展开图中的距离,就是这只小猫经过的最短距离.
【解答】解:由图可知,,
( http: / / www.21cnjy.com )
侧面展开是一个扇形.=120°.
∴∠A1CB=60°△A1CB是正三角形,
由D1是A1C的中点
∴BD1⊥A1C,CD1=3,BD1=,
∴小猫前行的最短距离是m.
【点评】本题考查了圆锥的计算,正确判断小猫经过的路线,把曲面的问题转化为平面的问题是解题的关键.
9.【分析】容易得出点A与点A′,B与B′重合;
矩形的对角线即为这条丝线最短的长度,由勾股定理即可得出答案;
连接AA′,根据弧长公式可得出圆心角的度数,由勾股定理可得出AA′;
将大树近似的看作圆柱将其展开,可得出紫藤的最短长度.
【解答】解:动手操作:易得点A与点A′,B与B′重合;
探究与发现:圆柱的底面周长是矩形的长,
∵圆柱的底面周长是40,高是30,
∴矩形的对角线为50,
∴这条丝线最短的长度是 50,
实践与应用:
连接AA′,
( http: / / www.21cnjy.com )
∵底面周长为π,∴弧长==π,
∴n=120°即∠AOA′=120°,
∴∠A=30°,
作OB⊥AA′于B,在Rt△OBA中,
∵OA=4,∴OB=2,
∴AB=2,
∴AA′=4;
拓展联想:
方法一:如图,紫藤的长为:=30米;
方法二:紫藤绕树干的周长为:=,
则8周的周长为:8×=30米,
故答案为A,B,50.
( http: / / www.21cnjy.com )
【点评】本题考查了圆锥的计算、圆柱的计算以及其实际应用,综合性较强难度偏大.
二、知识回顾 1.圆锥的侧面展开图圆锥的母线------扇形的 半径 圆锥的底面周长------扇形的 弧长 ( http: / / www.21cnjy.com )侧面展开得到的扇形的圆心角为 2. 平面上,两点之间,线段最短.
三、新知讲解 1. 圆锥中的展、围、转、剖圆锥是一种重要的几何体,与它相关的计算类型繁多,若能根据展、围、转、剖的特征学习圆锥,则这部分知识可迎刃而解.请看下面的解读.展——“展”就是把一个圆锥的侧面沿它的一 ( http: / / www.21cnjy.com )条母线剪开后展在一个平面上.圆锥的侧面展开图是一个扇形,此时圆锥的底面周长等于扇形的弧长,圆锥的母线长等于扇形的半径.围——“围”就是将扇形两边的半径拼到一起,围成一个圆锥,它与“展”恰好相反.此时,扇形的圆心就成了圆锥的顶点,扇形的半径就变成了圆锥的母线,扇形的弧长变成了圆锥底面圆的周长.下图是圆锥和圆锥的侧面展开图,体现了圆锥和扇形之间的转化关系,灵活理解“展”和“围”的过程,可以帮助同学们理解圆锥的侧面积和全面积的计算公式:S圆锥侧=S扇形=·2πr·l=πrl,S圆锥全=πrl+πr2. ( http: / / www.21cnjy.com )转——圆锥可以看做是由一个直角三角形旋转得 ( http: / / www.21cnjy.com )到的.旋转过程中直角三角形的一条直角边等于圆锥的高,另一条直角边等于圆锥的底面半径.如下图,右边的圆锥可以看成是Rt△ACD绕直角边AD旋转得到的,其中CD为圆锥的底面半径,斜边AC为圆锥的母线长. ( http: / / www.21cnjy.com )剖——“剖”就是将圆锥沿着它们的轴将它们一 ( http: / / www.21cnjy.com )分为二,所得到的截面(轴截面)是等腰三角形,这个等腰三角形的腰长等于圆锥的母线长,底边长等于圆锥的底面直径.2.圆锥侧面上路径最短问题解决圆锥侧面上的“最短路径”问题,关键是将圆锥的侧面展开得到与原侧面对应的平面图形,在平面图形中寻找最短路径.
四、典例探究 扫一扫,有惊喜哦!1.求从圆锥母线上一点出发绕圆锥侧面一周的最短路径长【例1】(2014 佛山校级模拟)已知圆锥的底面半径为r=20cm,高h=cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离. ( http: / / www.21cnjy.com )总结:解决圆锥侧面上路径最短问题的步骤:(1)展开-—将圆锥侧面(曲面)展开成扇形(平面);(2)连线-—在扇形中找到最短路径;(3)计算-—找直角三角形,利用勾股定理计算.练1.(2012 江干区一模)如图,一只纺锤可近似看作由两个圆锥拼合而成,AB=18,AD=9,r=3.(1)求纺锤的表面积;(2)一只蚂蚁要从C点出发绕这只纺锤爬一圈回到原地,求蚂蚁爬过的最短路线长. ( http: / / www.21cnjy.com )2.求从圆锥底面圆周上一点到对面母线或母线中点的最短路径长【例2】如图,已知圆锥的底面半径为9cm,PA=27cm,C为PB的中点,AB为底面直径,则在圆锥侧面上由点A到点C的最短路径是多少? ( http: / / www.21cnjy.com )总结:1. 解决圆锥侧面上路径最短问题的步骤:(1)展开-—将圆锥侧面(曲面)展开成扇形(平面);(2)连线-—在扇形中找到最短路径;(3)计算-—找直角三角形,利用勾股定理计算.2. 将圆锥侧面展开后,注意圆锥侧面上的有关元素与展开后的扇形上的有关元素要对应.练2.如图所示,已知圆锥底面半径r=10cm,母线长为40cm.(1)求它的侧面展开图的圆心角和表面积.(2)若一甲出从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么? ( http: / / www.21cnjy.com )
五、课后小测 一、选择题1.如图,已知圆锥的母线长OA=6,底面圆的半径为2,一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处.则小虫所走的最短距离为( ) ( http: / / www.21cnjy.com )A.12 B.4π C. D.2.(2015 虎林市校级 ( http: / / www.21cnjy.com )二模)一圆锥体形状的圣诞帽,母线长是30cm,底面圆的直径是15cm,点A为圆锥底面圆周上一点,从A点开始绕圆锥侧面缠一圈彩带回到A点,则彩带最少用( )厘米(接口处重合部分忽略不计)A.30πcm B.30cm C.15πcm D.15cm3.(2014 新泰市一模)如图,圆锥 ( http: / / www.21cnjy.com )的轴截面△ABC是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径BC=4cm,母线AB=6cm,则由点B出发,经过圆锥的侧面到达母线AC的最短路程是( ) ( http: / / www.21cnjy.com )A.cm B.6cm C.cm D.4cm二、填空题4.(2014 番禺区校级二模)圆 ( http: / / www.21cnjy.com )锥的底面半径是1,母线长是4,一只蜘蛛从底面圆周上的一点A出发沿圆锥的侧面爬行一周后回到A点,则蜘蛛爬行的最短路径的长是_________.三、解答题5.(2012秋 杭州期末)如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度. ( http: / / www.21cnjy.com )6.(2011秋 宁海县期中)圆锥 ( http: / / www.21cnjy.com )的底面半径是3,母线长是9,P是底面圆周上一点:从点P拉一根绳子绕圆锥侧面一周,再回到P点,求这根绳子的最短长度. ( http: / / www.21cnjy.com )7.(2010 桥西区模拟)如图,圆锥底面的半径为10cm,高为10cm.(1)求圆锥的全面积;(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离. ( http: / / www.21cnjy.com )8.(2010 巫山县模拟)如图,有一堆圆锥形的稻谷,垂直高度CO=m,底面⊙O的直径AB=4m,B处有一小猫想去捕捉母线AC中点D处的老鼠,求出小猫绕侧面前行的最短距离. ( http: / / www.21cnjy.com )9.(2011 张家口模拟)动手操作: ( http: / / www.21cnjy.com )如图①,把长为l、宽为h的矩形卷成以AB为高的圆柱形,则点A′与点A重合,点B′与点B重合;探究发现:如图②,圆柱的底面周长是40,高是30,若在 ( http: / / www.21cnjy.com )圆柱体的侧面绕一圈丝线作装饰,从下底面A出发,沿圆柱侧面绕一周到上底面B,则这条丝线最短的长度是50;实践与应用:如图③,圆锥的母线长为4,底面半径为,若在圆锥体的侧面绕一圈彩带做装饰,从圆锥的底面上的点A出发,沿圆锥侧面绕一周回到点A.求这条彩带最短的长度是多少?拓展联想:如图④,一颗古树上下粗细相 ( http: / / www.21cnjy.com )差不大,可以看成圆柱体.测得树干的周长为3米,高为18米,有一根紫藤自树底部均匀的盘绕在树干上,恰好绕8周到达树干的顶部,你能求出这条紫藤至少有多少米吗?
典例探究答案:
【例1】【分析】蚂蚁爬行 ( http: / / www.21cnjy.com )的最短距离是圆锥的展开图的扇形中AA′的长度.根据勾股定理求得母线长后,利用弧长等于底面周长求得扇形的圆心角的度数为90度,再由等腰直角三角形的性质求解.
【解答】解:设扇形的圆心角为n°,圆锥的顶为E,
( http: / / www.21cnjy.com )
∵r=20cm,h=cm
∴由勾股定理可得母线l==80cm,
而圆锥侧面展开后的扇形的弧长为2×20π=,
∴n=90
即△EAA′是等腰直角三角形,
∴由勾股定理得:AA'==80cm.
答:蚂蚁爬行的最短距离为80cm.
【点评】本题利用了勾股定理,弧长公式,圆的周长公式,等腰直角三角形的性质求解.
练1.【分析】(1)分别计算两个圆锥的侧面积后相加即可得到结果.
(2)首先求得展开扇形的圆心角的度数,然后分两种情况得到两种结果即可比较出最短线路的长.
【解答】解:(1)S=S1+S2=27π+54π=81π;(3分)
(2)∵,∴==120°,
连接CC′,过点D作CC′的垂线,垂足为E,
( http: / / www.21cnjy.com )
则由垂径定理可知CE=C′E,在直角三角形DEC中,∠CDE=30°,CD=9,
由勾股定理,可得:CE=,
∴CC′=2CE=2×9×=9.
如经左边,同理可得另一最短路线为18.
∵9<9×=9×2=18,
∴蚂蚁爬过的最短路线长为9.
【点评】本题考查了圆锥的计算,解题的关键是熟知圆锥的有关元素与扇形的有关元素的对应.
【例2】【分析】最短距离的问题首先应转 ( http: / / www.21cnjy.com )化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.
【解答】解:如图所示,
( http: / / www.21cnjy.com )
∴设圆心角为n°,则=2π×9,解得n=120.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90°.
∴∠CAP=30°,在△RtAPC中,利用勾股定理可得:
∴AC=.
答:由点A到点C的最短路径长是.
【点评】本题考查了圆锥的计算,需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.
练2.【分析】(1)利用圆锥的弧长等于 ( http: / / www.21cnjy.com )底面周长得到圆锥的侧面展开图的圆心角;圆锥表面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长;
(2)最短路线应放在平面内,构造直角三角形,求两点之间的线段的长度.
【解答】解:(1)=2π×10,
解得n=90.
圆锥表面积=π×102+π×10×40=500πcm2.
(2)如右图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
( http: / / www.21cnjy.com )
在Rt△ASB中,SA=40,SB=20,
∴AB=20(cm).
∴甲虫走的最短路线的长度是20cm.
【点评】用到的知识点为:圆锥的弧长 ( http: / / www.21cnjy.com )等于底面周长;求立体图形中两点之间的最短路线长,一般应放在平面内,构造直角三角形,求两点之间的线段的长度.
课后小测答案:
一、选择题
1.【分析】利用圆锥的底面周长等于侧面展开图的弧长可得圆锥侧面展开图的圆心角,求出侧面展开图中两点间的距离即为最短距离.
【解答】解:∵底面圆的半径为2,
∴圆锥的底面周长为2π×2=4π,
设圆锥的侧面展开图的圆心角为n.
∴=4π,
解得n=120°,
作OC⊥AA′于点C,
( http: / / www.21cnjy.com )
∴∠AOC=60°,
∴AC=OA×sin60°=3,
∴AA′=2AC=6.
故选D.
【点评】考查圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.
2.【分析】画出圆锥展开图,设扇形的圆心角∠ASA′=n°,根据弧长公式得到=2 π 15,解得n=90,则可判断△SAA′为等腰直角三角形,然后根据等腰直角三角形的性质求解.
【解答】解:如图,设扇形的圆心角∠ASA′=n°,
( http: / / www.21cnjy.com )
根据题意得=2 π 15,解得n=90,
所以△SAA′为等腰直角三角形,
所以AA′=SA=30,
即彩带最少用30厘米.
故选B.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
3.【分析】沿母线AB把圆锥展开,过B作 ( http: / / www.21cnjy.com )BD⊥AC′于D,根据两点之间线段最短,得到由点B出发,经过圆锥的侧面到达母线AC的最短路程为BD,BC′弧长为圆锥底面圆的周长的一半,再根据弧长公式计算出∠DAB,最后解Rt△ADB,即可得到BD.
【解答】解:沿母线AB把圆锥展开,如图,
过B作BD⊥AC′于D,
( http: / / www.21cnjy.com )
弧BC′= 2π 2=2π,
设∠C′AB=n°,
∴2π=,
∴n=60,即∠DAB=60°,
在Rt△ADB中,AD=AB=×6=3,
∴BD=AD=3,
所以由点B出发,经过圆锥的侧面到达母线AC的最短路程为3cm.
故选C.
【点评】本题考查了圆锥的展开图的有关 ( http: / / www.21cnjy.com )计算:展开图为扇形,弧长为圆锥底面圆的周长,半径为圆锥的母线长.也考查了把立体图形中的问题转化为平面图形来解决.
二、填空题
4.【分析】利用圆锥侧面展开图的弧长等于底面圆的周长,进而得出扇形圆心角的度数,再利用勾股定理求出AA′的长.
【解答】解:由题意可得出:OA=OA′=4,
( http: / / www.21cnjy.com )
==2π,
解得:n=90°,
∴∠AOA′=90°,
∴AA′==4,
故答案为:4.
【点评】此题主要考查了平面展开图的最短路径问题,得出∠AOA′的度数是解题关键.
三、解答题
5.【分析】(1)根据勾股定理直接求出圆锥的高,再利用圆锥侧面展开图弧长与其底面周长的长度关系,求出侧面展开图中∠ABC的度数即可;
(2)首先求出BD的长,再利用勾股定理求出AD以及AC的长即可.
【解答】解:(1)圆锥的高=,
底面圆的周长等于:2π×2=,
解得:n=120°;
(2)连结AC,过B作BD⊥AC于D,则∠ABD=60°.
( http: / / www.21cnjy.com )
由AB=6,可求得BD=3,
∴AD═,
AC=2AD=,
即这根绳子的最短长度是.
【点评】此题考查了圆锥的计算;得到圆锥的底面圆的周长和扇形弧长相等是解决本题的突破点.
6.【分析】圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对直径,转化为求直径的长的问题.
【解答】解:将圆锥侧面沿AB剪开展平,连BB′,则BB′就是所求绳子长.
( http: / / www.21cnjy.com )
由2π×3=得n=120,
作AC⊥BB',则∠2=60°BB'=2BC,
∴∠3=30°∴AC=,BC=,
∴BB′=.
【点评】本题主要考查圆锥的计算,圆锥的 ( http: / / www.21cnjy.com )侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
7.【分析】(1)首先求得圆锥的母线长,然后求得展开扇形的弧长,进而求得其侧面积和底面积,从而求得其全面积;
(2)将圆锥的侧面展开,求得其展开扇形的圆心角的度数是90°,利用勾股定理求得AM的长即为最短距离.
【解答】解:(1)由题意,可得圆锥的母线SA==40(cm)
圆锥的侧面展开扇形的弧长l=2π OA=20πcm
∴S侧=L SA=400πcm2
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(400+100)π=500π(cm2);
(2)沿母线SA将圆锥的侧面展开,如图,则线段AM的长就是蚂蚁所走的最短距离
( http: / / www.21cnjy.com )
由(1)知,SA=40cm,弧AA′=20πcm
∵=20πcm,
∴∠S=n==90°,
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
【点评】本题利用了勾股定理,弧长公式,圆的周长公式,等直角三角形的性质求解.
8.【分析】求这只小猫经过的最 ( http: / / www.21cnjy.com )短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为6cm的等边三角形可知,展开图是半径是6的半圆.点B是半圆的一个端点,而点P是平分半圆的半径的中点,根据勾股定理就可求出两点B和P在展开图中的距离,就是这只小猫经过的最短距离.
【解答】解:由图可知,,
( http: / / www.21cnjy.com )
侧面展开是一个扇形.=120°.
∴∠A1CB=60°△A1CB是正三角形,
由D1是A1C的中点
∴BD1⊥A1C,CD1=3,BD1=,
∴小猫前行的最短距离是m.
【点评】本题考查了圆锥的计算,正确判断小猫经过的路线,把曲面的问题转化为平面的问题是解题的关键.
9.【分析】容易得出点A与点A′,B与B′重合;
矩形的对角线即为这条丝线最短的长度,由勾股定理即可得出答案;
连接AA′,根据弧长公式可得出圆心角的度数,由勾股定理可得出AA′;
将大树近似的看作圆柱将其展开,可得出紫藤的最短长度.
【解答】解:动手操作:易得点A与点A′,B与B′重合;
探究与发现:圆柱的底面周长是矩形的长,
∵圆柱的底面周长是40,高是30,
∴矩形的对角线为50,
∴这条丝线最短的长度是 50,
实践与应用:
连接AA′,
( http: / / www.21cnjy.com )
∵底面周长为π,∴弧长==π,
∴n=120°即∠AOA′=120°,
∴∠A=30°,
作OB⊥AA′于B,在Rt△OBA中,
∵OA=4,∴OB=2,
∴AB=2,
∴AA′=4;
拓展联想:
方法一:如图,紫藤的长为:=30米;
方法二:紫藤绕树干的周长为:=,
则8周的周长为:8×=30米,
故答案为A,B,50.
( http: / / www.21cnjy.com )
【点评】本题考查了圆锥的计算、圆柱的计算以及其实际应用,综合性较强难度偏大.
同课章节目录
