第八章 立体几何初步章末检测试题(含解析)
文档属性
| 名称 | 第八章 立体几何初步章末检测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 537.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章 立体几何初步末检测试题(解析)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.本试卷共19小题,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题 共58分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.两个平行平面与另两个平行平面相交得四条直线的位置关系是( )
A.两两相互平行 B.两两相交于同一点
C.两两相交但不一定交于同一点 D.两两相互平行或交于同一点
2.如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′
=2O′B′,则以下说法正确的是( )
A.△ABC是钝角三角形 B.△ABC是等腰三角形,但不是直角三角形
C.△ABC是等腰直角三角形 D.△ABC是等边三角形
3.如图,在正方体ABCD - A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,
则异面直线AC与MN所成的角为( )
A.30° B.45° C.60° D.90°
4.《算数书》竹简于上世纪八十年代在我省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中有一道求“困盖”体积的题:困下周六丈高二丈,求积.即已知圆锥的底面周长为丈,高为丈,求圆锥的体积.《算数书》中将圆周率近似取为3,则该困盖的体积(单位:立方丈)约为( )
A.6 B. 4 C.3 D. 2
5.若一个正四棱锥的侧棱和底面边长相等,则该正四棱锥的侧棱和底面所成的角为( )
A.30° B.45° C.60° D.90°
6.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列命题:
①若m∥α,n∥β,α∥β,则m∥n; ②若α∥γ,β∥γ,则α∥β;
③若m⊥α,n⊥β,α∥β,则m∥n; ④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.①③ B.①④ C.②③ D.②④
7.如图,在棱长为1的正方体ABCD A1B1C1D1中,M,N分别是A1D1,A1B1中点,
过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
A. B. C. D.
8.在四面体A BCD中,AB=CD=10,AC=BD=2,AD=BC=2,则四面体A BCD外接球的表面积为( )
A.200π B.100π C. 50π D.300π
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
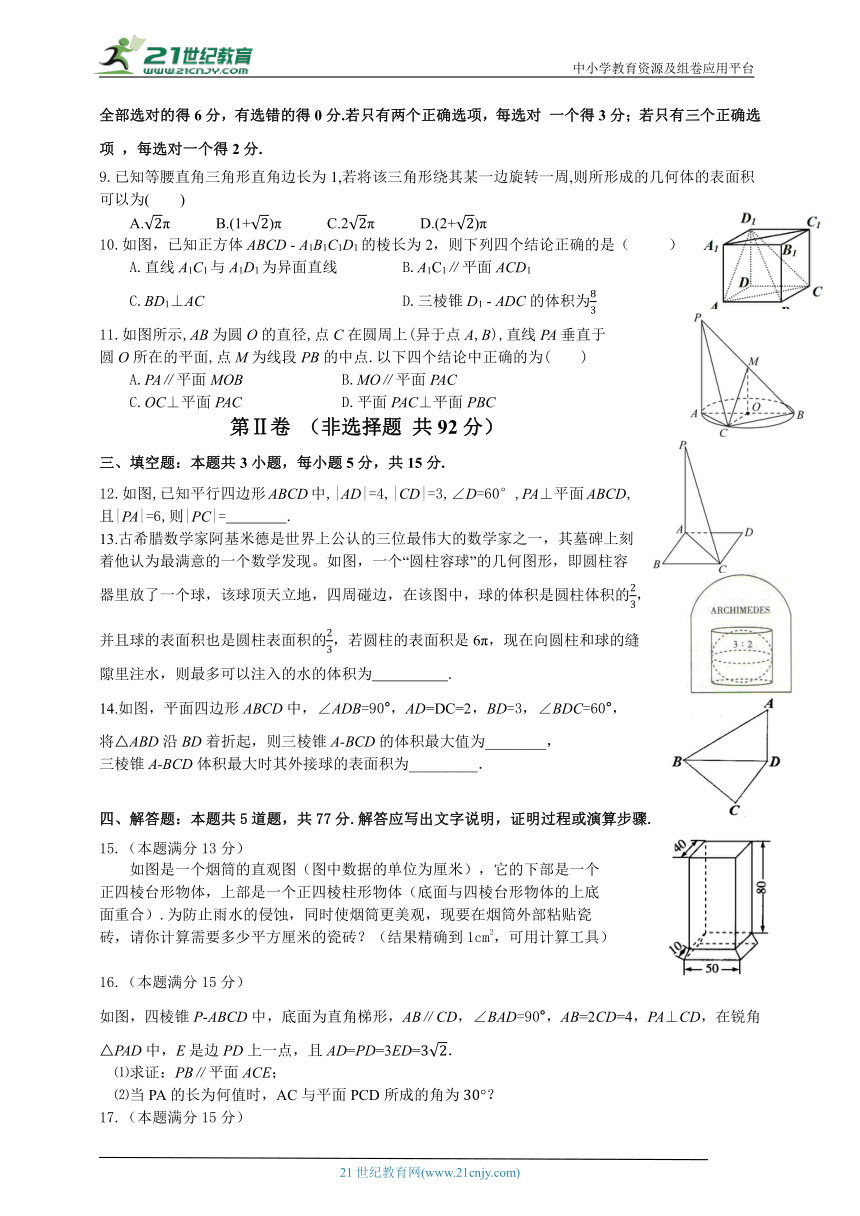
9.已知等腰直角三角形直角边长为1,若将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( )
A.π B.(1+)π C.2π D.(2+)π
10.如图,已知正方体ABCD - A1B1C1D1的棱长为2,则下列四个结论正确的是( )
A.直线A1C1与A1D1为异面直线 B.A1C1∥平面ACD1
C.BD1⊥AC D.三棱锥D1 - ADC的体积为
11.如图所示,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于
圆O所在的平面,点M为线段PB的中点.以下四个结论中正确的为( )
A.PA∥平面MOB B.MO∥平面PAC
C.OC⊥平面PAC D.平面PAC⊥平面PBC
第Ⅱ卷 (非选择题 共92分)
填空题:本题共3小题,每小题5分,共15分.
12.如图,已知平行四边形ABCD中,|AD|=4,|CD|=3,∠D=60°,PA⊥平面ABCD,
且|PA|=6,则|PC|= .
13.古希腊数学家阿基米德是世界上公认的三位最伟大的数学家之一,其墓碑上刻
着他认为最满意的一个数学发现。如图,一个“圆柱容球”的几何图形,即圆柱容
器里放了一个球,该球顶天立地,四周碰边,在该图中,球的体积是圆柱体积的,
并且球的表面积也是圆柱表面积的,若圆柱的表面积是6π,现在向圆柱和球的缝
隙里注水,则最多可以注入的水的体积为 .
14.如图,平面四边形ABCD中,∠ADB=90°,AD=DC=2,BD=3,∠BDC=60°,
将△ABD沿BD着折起,则三棱锥A-BCD的体积最大值为________,
三棱锥A-BCD体积最大时其外接球的表面积为_________.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分13分)
如图是一个烟筒的直观图(图中数据的单位为厘米),它的下部是一个
正四棱台形物体,上部是一个正四棱柱形物体(底面与四棱台形物体的上底
面重合).为防止雨水的侵蚀,同时使烟筒更美观,现要在烟筒外部粘贴瓷
砖,请你计算需要多少平方厘米的瓷砖?(结果精确到1cm2,可用计算工具)
16.(本题满分15分)
如图,四棱锥P-ABCD中,底面为直角梯形,AB∥CD,∠BAD=90°,AB=2CD=4,PA⊥CD,在锐角△PAD中,E是边PD上一点,且AD=PD=3ED=.
⑴求证:PB∥平面ACE;
⑵当PA的长为何值时,AC与平面PCD所成的角为?
17.(本题满分15分)
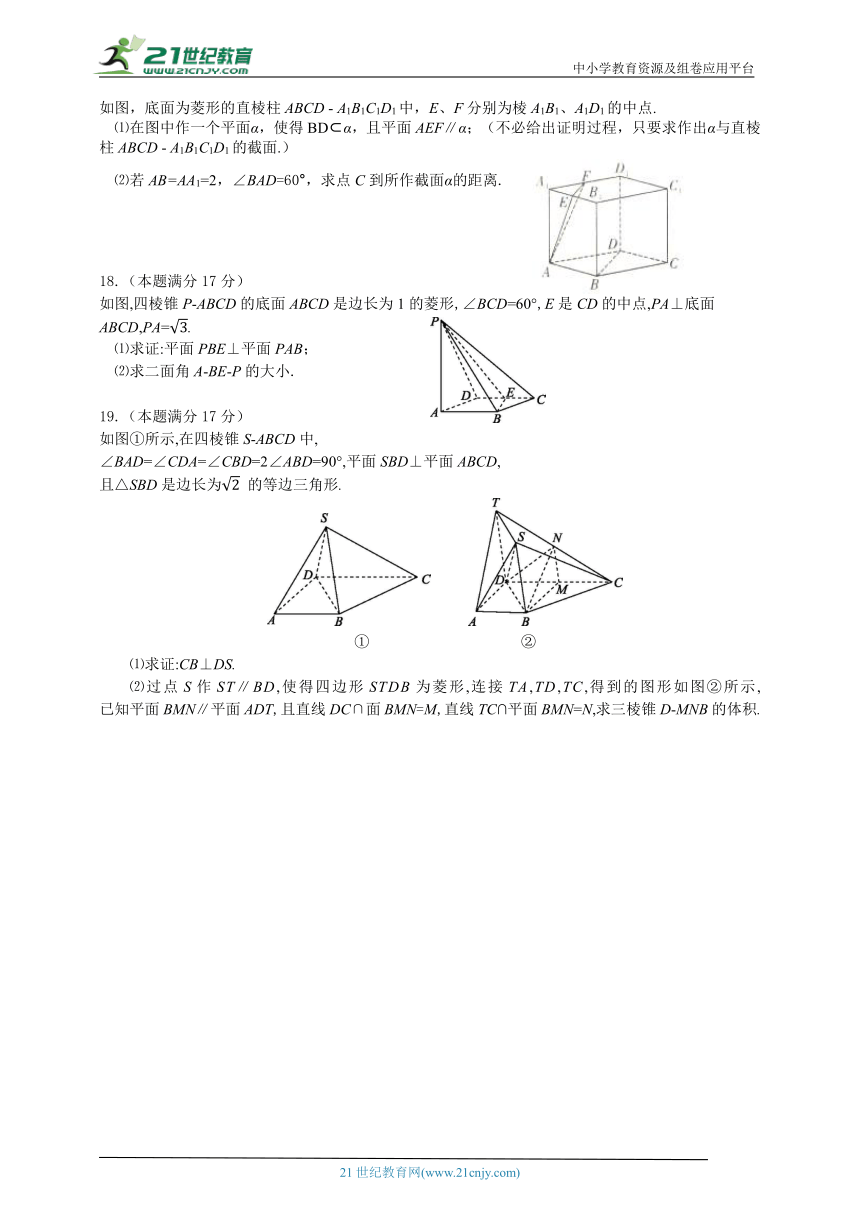
如图,底面为菱形的直棱柱ABCD - A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.
⑴在图中作一个平面α,使得BD α,且平面AEF∥α;(不必给出证明过程,只要求作出α与直棱柱ABCD - A1B1C1D1的截面.)
⑵若AB=AA1=2,∠BAD=60°,求点C到所作截面α的距离.
18.(本题满分17分)
如图,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=.
⑴求证:平面PBE⊥平面PAB;
⑵求二面角A-BE-P的大小.
19.(本题满分17分)
如图①所示,在四棱锥S-ABCD中,
∠BAD=∠CDA=∠CBD=2∠ABD=90°,平面SBD⊥平面ABCD,
且△SBD是边长为 的等边三角形.
① ②
⑴求证:CB⊥DS.
⑵过点S作ST∥BD,使得四边形STDB为菱形,连接TA,TD,TC,得到的图形如图②所示,
已知平面BMN∥平面ADT,且直线DC∩面BMN=M,直线TC∩平面BMN=N,求三棱锥D-MNB的体积.
试题解析
选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.两个平行平面与另两个平行平面相交得四条直线的位置关系是( )
A.两两相互平行 B.两两相交于同一点
C.两两相交但不一定交于同一点 D.两两相互平行或交于同一点
【答案】A.
【解析】根据平面与平面平行的性质可知,所得四条直线两两相互平行.故选A.
2.如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′
=2O′B′,则以下说法正确的是( )
A.△ABC是钝角三角形 B.△ABC是等腰三角形,但不是直角三角形
C.△ABC是等腰直角三角形 D.△ABC是等边三角
【答案】C
【解析】将其恢复成原图,设A′C′=2,则可得OB=2O′B′=1,
AC=A′C′=2,故△ABC是等腰直角三角形,故选C.
3.如图,在正方体ABCD - A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,
则异面直线AC与MN所成的角为( )
A.90° B.60° C. 45° D. 30°
【答案】B.
【解析】连接BC1,AD1,即MN∥BC1,BC1∥AD1,∴MN∥AD1,∠D1AC是异面直线AC与MN所成的角.由△AD1C是等边三角形,得∠D1AC=60°,∴异面直线AC与MN所成的角为60°,故选B.
4.《算数书》竹简于上世纪八十年代在我省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中有一道求“困盖”体积的题:困下周六丈高二丈,求积。即已知圆锥的底面周长为丈,高为丈,求圆锥的体积。《算数书》中将圆周率近似取为3,则该困盖的体积(单位:立方丈)约为( )
A.6 B. 4 C.3 D. 2
【答案】D.
【解析】设圆锥底面半径为r,则,
∴V=,故选D.
5..若一个正四棱锥的侧棱和底面边长相等,则该正四棱锥的侧棱和底面所成的角为( )
A.30° B.45° C.60° D.90°
【答案】B.
【解析】正四棱锥S-ABCD的侧棱和底面边长相等,作SO⊥底面ABCD,垂足为O,
∴∠SBO是该正四棱锥的侧棱和底面所成的角,
设AB=a,则SB=a,,∴,∠SBO=45°,∴该正四棱锥的侧棱和底面所成的角为45°.故选B.
6.下设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列命题:
①若m∥α,n∥β,α∥β,则m∥n; ②若α∥γ,β∥γ,则α∥β;
③若m⊥α,n⊥β,α∥β,则m∥n; ④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.①③ B.①④ C.②③ D.②④
【答案】C
【解析】若m∥α,n∥β,α∥β,则m,n可能平行,也可能相交或异面,①是错误的;若α⊥γ,β⊥γ,,也可能α⊥β,④错误;显然②③.故选C.
7.如图,在棱长为1的正方体ABCD A1B1C1D1中,M,N分别是A1D1,A1B1中点,
过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
A. B. C. D.
【答案】B
【解析】取C1D1,B1C1的中点分别为P,Q,连接PQ,PD,NP,QB,B1D1.
易知MN∥B1D1∥BD,AD∥NP,AD=NP,∴四边形ANPD为平行四边形,
则AN∥DP.又BD和DP为平面BDPQ的两条相交直线,∴平面BDPQ∥
平面AMN,即平面α为平面BDPQ.由PQ∥DB,PQ=BD=,
得四边形BDPQ为梯形,其高h= =.∴平面α截该正方体所得截面的面积为
(PQ+BD)h=××=.故选B.
8.在四面体A BCD中,AB=CD=10,AC=BD=2,AD=BC=2,则四面体A BCD外接球的表面积为( )
A.200π B.100π C. 50π D.300π
【答案】A.
【解析】∵四面体A BCD的四个面为全等的三角形,∴可将四面体A BCD置于一个长方体中,则四面体A BCD的外接球即为长方体的外接球,设长方体的长、宽、高分别为a,b,c,则有则外接球的直径2R= = =10 ,所以R=5 ,则球的表面积为S=4πR2=200π.故选A.
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.已知等腰直角三角形直角边长为1,若将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( )
A.π B.(1+)π C.2π D.(2+)π
【答案】AB
【解析】当以该三角形直角边为轴旋转一周,所得得圆锥是底面半径为1,母线长为,则其表面积为(1+)π;当以该三角形的斜边为轴旋转一周,所得几何体的表面是两个半径为,母线长为1的圆锥的侧面积,则其表面积为.故选AB.
10.如图,已知正方体ABCD - A1B1C1D1的棱长为2,则下列四个结论正确的是( )
A.直线A1C1与A1D1为异面直线 B.A1C1∥平面ACD1
C.BD1⊥AC D.三棱锥D1 - ADC的体积为
【答案】BC
【解析】显然,直线A1C1与A1D1为相交直线,A选项错误; ∵A1C1∥AC,AC 平面ACD1,
∴A1C1∥平面ACD1,B选项正确;∵AC⊥BD,B1B⊥AC,BD∩B1B=B,∴AC⊥平面BB1D1D,
又BD1 平面BB1D1D,∴AC⊥BD1,C选项正确;V三棱锥D1 - ADC=,D选项错误.
故选BC.
11.如图所示,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于
圆O所在的平面,点M为线段PB的中点.以下四个结论中正确的为( )
A.PA∥平面MOB B.MO∥平面PAC
C.OC⊥平面PAC D.平面PAC⊥平面PBC
【答案】BD
【解析】∵PA 平面MOB,∴选项A不正确;∵MO∥PA,且MO 平面PAC,选项B正确;∵OC不垂直于AC,∴选项C不正确;∵BC⊥AC,BC⊥PA,AC∩PA=A,∴BC⊥平面PAC,∴平面PAC⊥平面PBC,选项D正确.故选BD.
填空题:本题共3小题,每小题5分,共15分.
12.如图,已知平行四边形ABCD中,|AD|=4,|CD|=3,∠D=60°,PA⊥平面ABCD,
且|PA|=6,则|PC|= .
【答案】7
【解析】由余弦定理,得AC2=AD2+CD2-2AD·CD·cos∠D=16+9-2×4×3×=13,
∴AC=,∵PA⊥平面ABCD,AC 平面ABCD,∴PA⊥AC,PC==7.
13.古希腊数学家阿基米德是世界上公认的三位最伟大的数学家之一,其墓碑上刻
着他认为最满意的一个数学发现。如图,一个“圆柱容球”的几何图形,即圆柱容
器里放了一个球,该球顶天立地,四周碰边,在该图中,球的体积是圆柱体积的,
并且球的表面积也是圆柱表面积的,若圆柱的表面积是6π,现在向圆柱和球的缝
隙里注水,则最多可以注入的水的体积为 .
【答案】
【解析】设球的半径为r,则由题意可得球的表面积为,∴r=1,
∴圆柱的底面半径为1,高为2,
∴最多可以注入的水的体积为.
14.如图,平面四边形ABCD中,∠ADB=90°,AD=DC=2,BD=3,∠BDC=60°,
将△ABD沿BD着折起,则三棱锥A-BCD的体积最大值为________,
三棱锥A-BCD体积最大时其外接球的表面积为_________.
【答案】;.
【解析】①由题意作出平面图及翻折后的图形.
∵三棱锥A-BCD的底面△BCD的面积是定值,
∴当点A离平面BCD的距离最大,即当平面ADB⊥平面BCD时,VA-BCD最大.
又∵∠ADB=90°,即AD⊥BD,平面ADB∩平面BCD=BD,∴AD⊥平面BCD,即AD为高.
∴Vmax=.
②.侧棱垂直于底面且底面是由普通三角形的三棱锥外接球球心满足OO′=AD,
O为球心,为O′底面△BCD外接圆圆心,
在△BCD中,由余弦定理得BC2=BD2+CD2-2BD CD cos∠BDC=7,BC=,
由正弦定理得D,O′D=.设外接球的半径为R,
在Rt△OO′D中,,S表=4πR2=.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 如图是一个烟筒的直观图(图中数据的单位为厘米),它的下部是一个
正四棱台形物体,上部是一个正四棱柱形物体(底面与四棱台形物体的上底
面重合).为防止雨水的侵蚀,同时使烟筒更美观,现要在烟筒外部粘贴瓷
砖,请你计算需要多少平方厘米的瓷砖?(结果精确到1cm2,可用计算工具).
【答案】14359(cm2).
【解析】由题意,需贴瓷砖的部分为四棱柱与四棱台的侧面积.
,
四棱台的斜高,
需要瓷砖的面积为12800+1559=14359(cm2)
16.如图,四棱锥P-ABCD中,底面为直角梯形,AB∥CD,∠BAD=90°,AB=2CD=4,PA⊥CD,在锐角△PAD中,E是边PD上一点,且AD=PD=3ED=.
⑴求证:PB∥平面ACE;
⑵当PA的长为何值时,AC与平面PCD所成的角为?
【答案】⑴详见解析; ⑵当PA=时,AC与平面PCD所成的角为30°.
【解析】⑴证明:连接BD交AC于O,
∵AB∥CD,∴△OCD∽△OAB,
∴=,又=,
∴OE∥PB,又OE 平面ACE,PB 平面ACE,
∴PB∥平面ACE.
⑵解:过A作AF⊥PD,垂足为F,连接CF,
∵CD⊥AD,CD⊥PA,PA∩AD=A,
∴CD⊥平面PAD,∴CD⊥AF,
又AF⊥PD,PD∩CD=D,
∴AF⊥平面PCD,∴∠ACF为AC与平面PCD所成的角,即∠ACF=30°.
AC==,∴AF=AC=,
∴sin∠ADF==,cos∠ADF==,
∴PA==.
∴当PA=时,AC与平面PCD所成的角为30°.
17.如图,底面为菱形的直棱柱ABCD - A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.
⑴在图中作一个平面α,使得BD α,且平面AEF∥α;(不必给出证明过程,只要求作出α与直棱柱ABCD - A1B1C1D1的截面.)
⑵若AB=AA1=2,∠BAD=60°,求点C到所作截面α的距离.
【答案】⑴详见解析;⑵.
【解析】⑴如图,取B1C1、C1D1的中点M、N,连接BM、MN、ND,
则平面BMND即为所求平面;
⑵设点C到平面BMND的距离为h,由等体积法得:,
又,
∵,又,
∴,
又由得 ,
∴.
18.如图,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=.
⑴求证:平面PBE⊥平面PAB;
⑵求二面角A-BE-P的大小.
【答案】⑴详细证明见解析; ⑵60°.
【解析】⑴证明:如图,连接BD.
由四边形ABCD是菱形,且∠BCD=60°,可知△BCD是等边三角形.
∵E是CD的中点,∴BE⊥CD,
∵AB∥CD,∴BE⊥AB.
∵PA⊥平面ABCD,BE 平面ABCD,
∴PA⊥BE.
又PA 平面PAB,AB 平面PAB,PA∩AB=A,
∴BE⊥平面PAB.
∵BE 平面PBE,
∴平面PBE⊥平面PAB.
⑵解:由⑴知BE⊥平面PAB,PB 平面PAB,
∴PB⊥BE,
∵AB⊥BE,
∴∠PBA是二面角A-BE-P的平面角.
在Rt△PAB中, tan∠PBA===,
∴∠PBA=60°,
故二面角A-BE-P的大小是60°.
19.如图①所示,在四棱锥S-ABCD中,
∠BAD=∠CDA=∠CBD=2∠ABD=90°,平面SBD⊥平面ABCD,
且△SBD是边长为 的等边三角形.
① ②
⑴求证:CB⊥DS.
⑵过点S作ST∥BD,使得四边形STDB为菱形,连接TA,TD,TC,得到的图形如图②所示,
已知平面BMN∥平面ADT,且直线DC∩面BMN=M,直线TC∩平面BMN=N,求三棱锥D-MNB的体积.
【答案】⑴详见解析;⑵.
【解析】⑴证明:∵∠CBD=90°,
∴CB⊥BD.
∵平面SBD⊥平面ABCD,平面SBD∩平面ABCD=BD,CB 平面ABCD,
∴CB⊥平面SBD.
∵SD 平面SBD,
∴CB⊥DS.
⑵解:如图,取BD的中点为O,连接SO,SM,TB,TM.
由平面BMN∥平面ADT,得AD∥BM,DT∥MN.
∵∠CDA=90°,
∴∠BMD=90°,即BM⊥CD.
∵∠BAD=∠CDA=90°, ∴AB∥CD.
∵∠CBD=2∠ABD=90°, ∴∠ABD=∠CDB=45°,
即△CBD为等腰直角三角形. ∴DM=MC=1.
∵在△CDT中,MN∥DT,M是DC的中点,
∴N是TC的中点.
∴V三棱锥D-MNB=V三棱锥N-DMB=V三棱锥T-DMB=V三棱锥S-DMB.
∵DS=DB=BS, ∴SO⊥DB.
∵平面SBD⊥平面ABCD,平面SBD∩平面ABCD=DB,
∴SO⊥平面ABCD,
∴V三棱锥D-MNB= V三棱锥S-DMB=××SO×S△BDM=×× = .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 立体几何初步末检测试题(解析)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.本试卷共19小题,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题 共58分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.两个平行平面与另两个平行平面相交得四条直线的位置关系是( )
A.两两相互平行 B.两两相交于同一点
C.两两相交但不一定交于同一点 D.两两相互平行或交于同一点
2.如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′
=2O′B′,则以下说法正确的是( )
A.△ABC是钝角三角形 B.△ABC是等腰三角形,但不是直角三角形
C.△ABC是等腰直角三角形 D.△ABC是等边三角形
3.如图,在正方体ABCD - A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,
则异面直线AC与MN所成的角为( )
A.30° B.45° C.60° D.90°
4.《算数书》竹简于上世纪八十年代在我省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中有一道求“困盖”体积的题:困下周六丈高二丈,求积.即已知圆锥的底面周长为丈,高为丈,求圆锥的体积.《算数书》中将圆周率近似取为3,则该困盖的体积(单位:立方丈)约为( )
A.6 B. 4 C.3 D. 2
5.若一个正四棱锥的侧棱和底面边长相等,则该正四棱锥的侧棱和底面所成的角为( )
A.30° B.45° C.60° D.90°
6.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列命题:
①若m∥α,n∥β,α∥β,则m∥n; ②若α∥γ,β∥γ,则α∥β;
③若m⊥α,n⊥β,α∥β,则m∥n; ④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.①③ B.①④ C.②③ D.②④
7.如图,在棱长为1的正方体ABCD A1B1C1D1中,M,N分别是A1D1,A1B1中点,
过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
A. B. C. D.
8.在四面体A BCD中,AB=CD=10,AC=BD=2,AD=BC=2,则四面体A BCD外接球的表面积为( )
A.200π B.100π C. 50π D.300π
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.已知等腰直角三角形直角边长为1,若将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( )
A.π B.(1+)π C.2π D.(2+)π
10.如图,已知正方体ABCD - A1B1C1D1的棱长为2,则下列四个结论正确的是( )
A.直线A1C1与A1D1为异面直线 B.A1C1∥平面ACD1
C.BD1⊥AC D.三棱锥D1 - ADC的体积为
11.如图所示,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于
圆O所在的平面,点M为线段PB的中点.以下四个结论中正确的为( )
A.PA∥平面MOB B.MO∥平面PAC
C.OC⊥平面PAC D.平面PAC⊥平面PBC
第Ⅱ卷 (非选择题 共92分)
填空题:本题共3小题,每小题5分,共15分.
12.如图,已知平行四边形ABCD中,|AD|=4,|CD|=3,∠D=60°,PA⊥平面ABCD,
且|PA|=6,则|PC|= .
13.古希腊数学家阿基米德是世界上公认的三位最伟大的数学家之一,其墓碑上刻
着他认为最满意的一个数学发现。如图,一个“圆柱容球”的几何图形,即圆柱容
器里放了一个球,该球顶天立地,四周碰边,在该图中,球的体积是圆柱体积的,
并且球的表面积也是圆柱表面积的,若圆柱的表面积是6π,现在向圆柱和球的缝
隙里注水,则最多可以注入的水的体积为 .
14.如图,平面四边形ABCD中,∠ADB=90°,AD=DC=2,BD=3,∠BDC=60°,
将△ABD沿BD着折起,则三棱锥A-BCD的体积最大值为________,
三棱锥A-BCD体积最大时其外接球的表面积为_________.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分13分)
如图是一个烟筒的直观图(图中数据的单位为厘米),它的下部是一个
正四棱台形物体,上部是一个正四棱柱形物体(底面与四棱台形物体的上底
面重合).为防止雨水的侵蚀,同时使烟筒更美观,现要在烟筒外部粘贴瓷
砖,请你计算需要多少平方厘米的瓷砖?(结果精确到1cm2,可用计算工具)
16.(本题满分15分)
如图,四棱锥P-ABCD中,底面为直角梯形,AB∥CD,∠BAD=90°,AB=2CD=4,PA⊥CD,在锐角△PAD中,E是边PD上一点,且AD=PD=3ED=.
⑴求证:PB∥平面ACE;
⑵当PA的长为何值时,AC与平面PCD所成的角为?
17.(本题满分15分)
如图,底面为菱形的直棱柱ABCD - A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.
⑴在图中作一个平面α,使得BD α,且平面AEF∥α;(不必给出证明过程,只要求作出α与直棱柱ABCD - A1B1C1D1的截面.)
⑵若AB=AA1=2,∠BAD=60°,求点C到所作截面α的距离.
18.(本题满分17分)
如图,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=.
⑴求证:平面PBE⊥平面PAB;
⑵求二面角A-BE-P的大小.
19.(本题满分17分)
如图①所示,在四棱锥S-ABCD中,
∠BAD=∠CDA=∠CBD=2∠ABD=90°,平面SBD⊥平面ABCD,
且△SBD是边长为 的等边三角形.
① ②
⑴求证:CB⊥DS.
⑵过点S作ST∥BD,使得四边形STDB为菱形,连接TA,TD,TC,得到的图形如图②所示,
已知平面BMN∥平面ADT,且直线DC∩面BMN=M,直线TC∩平面BMN=N,求三棱锥D-MNB的体积.
试题解析
选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.两个平行平面与另两个平行平面相交得四条直线的位置关系是( )
A.两两相互平行 B.两两相交于同一点
C.两两相交但不一定交于同一点 D.两两相互平行或交于同一点
【答案】A.
【解析】根据平面与平面平行的性质可知,所得四条直线两两相互平行.故选A.
2.如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′
=2O′B′,则以下说法正确的是( )
A.△ABC是钝角三角形 B.△ABC是等腰三角形,但不是直角三角形
C.△ABC是等腰直角三角形 D.△ABC是等边三角
【答案】C
【解析】将其恢复成原图,设A′C′=2,则可得OB=2O′B′=1,
AC=A′C′=2,故△ABC是等腰直角三角形,故选C.
3.如图,在正方体ABCD - A1B1C1D1中,M,N分别为棱BC和棱CC1的中点,
则异面直线AC与MN所成的角为( )
A.90° B.60° C. 45° D. 30°
【答案】B.
【解析】连接BC1,AD1,即MN∥BC1,BC1∥AD1,∴MN∥AD1,∠D1AC是异面直线AC与MN所成的角.由△AD1C是等边三角形,得∠D1AC=60°,∴异面直线AC与MN所成的角为60°,故选B.
4.《算数书》竹简于上世纪八十年代在我省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中有一道求“困盖”体积的题:困下周六丈高二丈,求积。即已知圆锥的底面周长为丈,高为丈,求圆锥的体积。《算数书》中将圆周率近似取为3,则该困盖的体积(单位:立方丈)约为( )
A.6 B. 4 C.3 D. 2
【答案】D.
【解析】设圆锥底面半径为r,则,
∴V=,故选D.
5..若一个正四棱锥的侧棱和底面边长相等,则该正四棱锥的侧棱和底面所成的角为( )
A.30° B.45° C.60° D.90°
【答案】B.
【解析】正四棱锥S-ABCD的侧棱和底面边长相等,作SO⊥底面ABCD,垂足为O,
∴∠SBO是该正四棱锥的侧棱和底面所成的角,
设AB=a,则SB=a,,∴,∠SBO=45°,∴该正四棱锥的侧棱和底面所成的角为45°.故选B.
6.下设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列命题:
①若m∥α,n∥β,α∥β,则m∥n; ②若α∥γ,β∥γ,则α∥β;
③若m⊥α,n⊥β,α∥β,则m∥n; ④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是( )
A.①③ B.①④ C.②③ D.②④
【答案】C
【解析】若m∥α,n∥β,α∥β,则m,n可能平行,也可能相交或异面,①是错误的;若α⊥γ,β⊥γ,,也可能α⊥β,④错误;显然②③.故选C.
7.如图,在棱长为1的正方体ABCD A1B1C1D1中,M,N分别是A1D1,A1B1中点,
过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
A. B. C. D.
【答案】B
【解析】取C1D1,B1C1的中点分别为P,Q,连接PQ,PD,NP,QB,B1D1.
易知MN∥B1D1∥BD,AD∥NP,AD=NP,∴四边形ANPD为平行四边形,
则AN∥DP.又BD和DP为平面BDPQ的两条相交直线,∴平面BDPQ∥
平面AMN,即平面α为平面BDPQ.由PQ∥DB,PQ=BD=,
得四边形BDPQ为梯形,其高h= =.∴平面α截该正方体所得截面的面积为
(PQ+BD)h=××=.故选B.
8.在四面体A BCD中,AB=CD=10,AC=BD=2,AD=BC=2,则四面体A BCD外接球的表面积为( )
A.200π B.100π C. 50π D.300π
【答案】A.
【解析】∵四面体A BCD的四个面为全等的三角形,∴可将四面体A BCD置于一个长方体中,则四面体A BCD的外接球即为长方体的外接球,设长方体的长、宽、高分别为a,b,c,则有则外接球的直径2R= = =10 ,所以R=5 ,则球的表面积为S=4πR2=200π.故选A.
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.已知等腰直角三角形直角边长为1,若将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( )
A.π B.(1+)π C.2π D.(2+)π
【答案】AB
【解析】当以该三角形直角边为轴旋转一周,所得得圆锥是底面半径为1,母线长为,则其表面积为(1+)π;当以该三角形的斜边为轴旋转一周,所得几何体的表面是两个半径为,母线长为1的圆锥的侧面积,则其表面积为.故选AB.
10.如图,已知正方体ABCD - A1B1C1D1的棱长为2,则下列四个结论正确的是( )
A.直线A1C1与A1D1为异面直线 B.A1C1∥平面ACD1
C.BD1⊥AC D.三棱锥D1 - ADC的体积为
【答案】BC
【解析】显然,直线A1C1与A1D1为相交直线,A选项错误; ∵A1C1∥AC,AC 平面ACD1,
∴A1C1∥平面ACD1,B选项正确;∵AC⊥BD,B1B⊥AC,BD∩B1B=B,∴AC⊥平面BB1D1D,
又BD1 平面BB1D1D,∴AC⊥BD1,C选项正确;V三棱锥D1 - ADC=,D选项错误.
故选BC.
11.如图所示,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于
圆O所在的平面,点M为线段PB的中点.以下四个结论中正确的为( )
A.PA∥平面MOB B.MO∥平面PAC
C.OC⊥平面PAC D.平面PAC⊥平面PBC
【答案】BD
【解析】∵PA 平面MOB,∴选项A不正确;∵MO∥PA,且MO 平面PAC,选项B正确;∵OC不垂直于AC,∴选项C不正确;∵BC⊥AC,BC⊥PA,AC∩PA=A,∴BC⊥平面PAC,∴平面PAC⊥平面PBC,选项D正确.故选BD.
填空题:本题共3小题,每小题5分,共15分.
12.如图,已知平行四边形ABCD中,|AD|=4,|CD|=3,∠D=60°,PA⊥平面ABCD,
且|PA|=6,则|PC|= .
【答案】7
【解析】由余弦定理,得AC2=AD2+CD2-2AD·CD·cos∠D=16+9-2×4×3×=13,
∴AC=,∵PA⊥平面ABCD,AC 平面ABCD,∴PA⊥AC,PC==7.
13.古希腊数学家阿基米德是世界上公认的三位最伟大的数学家之一,其墓碑上刻
着他认为最满意的一个数学发现。如图,一个“圆柱容球”的几何图形,即圆柱容
器里放了一个球,该球顶天立地,四周碰边,在该图中,球的体积是圆柱体积的,
并且球的表面积也是圆柱表面积的,若圆柱的表面积是6π,现在向圆柱和球的缝
隙里注水,则最多可以注入的水的体积为 .
【答案】
【解析】设球的半径为r,则由题意可得球的表面积为,∴r=1,
∴圆柱的底面半径为1,高为2,
∴最多可以注入的水的体积为.
14.如图,平面四边形ABCD中,∠ADB=90°,AD=DC=2,BD=3,∠BDC=60°,
将△ABD沿BD着折起,则三棱锥A-BCD的体积最大值为________,
三棱锥A-BCD体积最大时其外接球的表面积为_________.
【答案】;.
【解析】①由题意作出平面图及翻折后的图形.
∵三棱锥A-BCD的底面△BCD的面积是定值,
∴当点A离平面BCD的距离最大,即当平面ADB⊥平面BCD时,VA-BCD最大.
又∵∠ADB=90°,即AD⊥BD,平面ADB∩平面BCD=BD,∴AD⊥平面BCD,即AD为高.
∴Vmax=.
②.侧棱垂直于底面且底面是由普通三角形的三棱锥外接球球心满足OO′=AD,
O为球心,为O′底面△BCD外接圆圆心,
在△BCD中,由余弦定理得BC2=BD2+CD2-2BD CD cos∠BDC=7,BC=,
由正弦定理得D,O′D=.设外接球的半径为R,
在Rt△OO′D中,,S表=4πR2=.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 如图是一个烟筒的直观图(图中数据的单位为厘米),它的下部是一个
正四棱台形物体,上部是一个正四棱柱形物体(底面与四棱台形物体的上底
面重合).为防止雨水的侵蚀,同时使烟筒更美观,现要在烟筒外部粘贴瓷
砖,请你计算需要多少平方厘米的瓷砖?(结果精确到1cm2,可用计算工具).
【答案】14359(cm2).
【解析】由题意,需贴瓷砖的部分为四棱柱与四棱台的侧面积.
,
四棱台的斜高,
需要瓷砖的面积为12800+1559=14359(cm2)
16.如图,四棱锥P-ABCD中,底面为直角梯形,AB∥CD,∠BAD=90°,AB=2CD=4,PA⊥CD,在锐角△PAD中,E是边PD上一点,且AD=PD=3ED=.
⑴求证:PB∥平面ACE;
⑵当PA的长为何值时,AC与平面PCD所成的角为?
【答案】⑴详见解析; ⑵当PA=时,AC与平面PCD所成的角为30°.
【解析】⑴证明:连接BD交AC于O,
∵AB∥CD,∴△OCD∽△OAB,
∴=,又=,
∴OE∥PB,又OE 平面ACE,PB 平面ACE,
∴PB∥平面ACE.
⑵解:过A作AF⊥PD,垂足为F,连接CF,
∵CD⊥AD,CD⊥PA,PA∩AD=A,
∴CD⊥平面PAD,∴CD⊥AF,
又AF⊥PD,PD∩CD=D,
∴AF⊥平面PCD,∴∠ACF为AC与平面PCD所成的角,即∠ACF=30°.
AC==,∴AF=AC=,
∴sin∠ADF==,cos∠ADF==,
∴PA==.
∴当PA=时,AC与平面PCD所成的角为30°.
17.如图,底面为菱形的直棱柱ABCD - A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点.
⑴在图中作一个平面α,使得BD α,且平面AEF∥α;(不必给出证明过程,只要求作出α与直棱柱ABCD - A1B1C1D1的截面.)
⑵若AB=AA1=2,∠BAD=60°,求点C到所作截面α的距离.
【答案】⑴详见解析;⑵.
【解析】⑴如图,取B1C1、C1D1的中点M、N,连接BM、MN、ND,
则平面BMND即为所求平面;
⑵设点C到平面BMND的距离为h,由等体积法得:,
又,
∵,又,
∴,
又由得 ,
∴.
18.如图,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=.
⑴求证:平面PBE⊥平面PAB;
⑵求二面角A-BE-P的大小.
【答案】⑴详细证明见解析; ⑵60°.
【解析】⑴证明:如图,连接BD.
由四边形ABCD是菱形,且∠BCD=60°,可知△BCD是等边三角形.
∵E是CD的中点,∴BE⊥CD,
∵AB∥CD,∴BE⊥AB.
∵PA⊥平面ABCD,BE 平面ABCD,
∴PA⊥BE.
又PA 平面PAB,AB 平面PAB,PA∩AB=A,
∴BE⊥平面PAB.
∵BE 平面PBE,
∴平面PBE⊥平面PAB.
⑵解:由⑴知BE⊥平面PAB,PB 平面PAB,
∴PB⊥BE,
∵AB⊥BE,
∴∠PBA是二面角A-BE-P的平面角.
在Rt△PAB中, tan∠PBA===,
∴∠PBA=60°,
故二面角A-BE-P的大小是60°.
19.如图①所示,在四棱锥S-ABCD中,
∠BAD=∠CDA=∠CBD=2∠ABD=90°,平面SBD⊥平面ABCD,
且△SBD是边长为 的等边三角形.
① ②
⑴求证:CB⊥DS.
⑵过点S作ST∥BD,使得四边形STDB为菱形,连接TA,TD,TC,得到的图形如图②所示,
已知平面BMN∥平面ADT,且直线DC∩面BMN=M,直线TC∩平面BMN=N,求三棱锥D-MNB的体积.
【答案】⑴详见解析;⑵.
【解析】⑴证明:∵∠CBD=90°,
∴CB⊥BD.
∵平面SBD⊥平面ABCD,平面SBD∩平面ABCD=BD,CB 平面ABCD,
∴CB⊥平面SBD.
∵SD 平面SBD,
∴CB⊥DS.
⑵解:如图,取BD的中点为O,连接SO,SM,TB,TM.
由平面BMN∥平面ADT,得AD∥BM,DT∥MN.
∵∠CDA=90°,
∴∠BMD=90°,即BM⊥CD.
∵∠BAD=∠CDA=90°, ∴AB∥CD.
∵∠CBD=2∠ABD=90°, ∴∠ABD=∠CDB=45°,
即△CBD为等腰直角三角形. ∴DM=MC=1.
∵在△CDT中,MN∥DT,M是DC的中点,
∴N是TC的中点.
∴V三棱锥D-MNB=V三棱锥N-DMB=V三棱锥T-DMB=V三棱锥S-DMB.
∵DS=DB=BS, ∴SO⊥DB.
∵平面SBD⊥平面ABCD,平面SBD∩平面ABCD=DB,
∴SO⊥平面ABCD,
∴V三棱锥D-MNB= V三棱锥S-DMB=××SO×S△BDM=×× = .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
