山东省淄博市临淄区2023—2024 学年度第二学期期中质量检测初四数学试题(图片版含答案)
文档属性
| 名称 | 山东省淄博市临淄区2023—2024 学年度第二学期期中质量检测初四数学试题(图片版含答案) |

|
|
| 格式 | |||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 00:00:00 | ||
图片预览



文档简介
2023—2024 学年度第二学期期中质量检测
初 四 数 学 试 题
本试卷共 8 页,满分 150 分,考试时间 120 分钟.考试结束后。
注意事项:
1.答题前,考生务必用 0.5 毫米黑色签字笔将学校、班级、姓名、考试号、座号填写
在答题卡和试卷规定位置。
2. 选择题每小题选出答案后,用 2B 铅笔涂黑答题卡对应题目的答案标号;如需改
动,用橡皮擦干净后,再选涂其他答案标号。
3.非选择题必须用 0.5 毫米黑色签字笔作答,字体工整、笔迹清晰,写在答题卡各题
目指定区域内;如需改动,先划掉原来答案,然后再写上新答案。严禁使用涂改液、胶带
纸、修正带修改。
4.保证答题卡清洁、完整,严禁折叠,严禁在答题卡上做任何标记。
5.评分以答题卡上的答案为依据。不按以上要求作答的答案无效。
一、 选择题(本题共 10 小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确
的选项填在下面的表中.每小题 4 分, 满分 40 分,错选、不选、多选,均记 0 分.)
1. 某体育场有 10000 个座位,10000 用科学记数法表示为
A.1×104 B. 0.1×105 C.10×104 D.10×103
2.下列几何图形中,是轴对称图形但不是中心对称图形的有
A.4 个
B.3 个
C.2 个
D.1 个
下列运算正确的是 (第 2 题图) 3.
A.a a2=a3 B.3a-a=3 C.a4÷a3=a2 D.(a3)2=a5
4. 一组数据 3,3,4,6,8,9 的中位数是
A.4 B.5 C.5.5 D.6
x 3 0
5. 不等式组 的解集在数轴上表示正确的是
2x 4 0
A. B.
C. D.
6.如图,直线 a∥b,若∠1=24°,∠A=46°,则∠2 的度数为
A.70° B.46° C.40° D.30° (第 6 题图)
初四数学第 1 页(共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
k
7. 设点 A(x1,y1)和点 B(x2,y2)是反比例函数 y 图象上的两点,当 x1<x2<0 时,
x
y1>y2,则一次函数 y=-2x+k 的图象不经过的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.甲、乙两人沿着总长度为 10km 的“健身步道”健步走,甲的速度是乙的 1.2 倍,甲比乙
提前 12 分钟走完全程.设乙的速度为 x km/h,则下列方程中正确的是
10 10 10 10 10 10 10 10
A. 12 B. 0.2 C. 12 D. 0.2
x 1.2x 1.2x x 1.2x x x 1.2x
9.如图,将矩形纸片 ABCD 折叠,使点 B 与点 D 重合,折痕为 MN,若 AB=2,BC=4,
那么线段 MN 的长为
2 5 4 5
A. B. 5 C. D. 2 5
5 5
(第 9 题图) (第 10 题图)
10.如图,四边形 ABCD 内接于⊙O,AC 为直径,∠ABC 的平分线 BD 交 AC 于点 E,
点 F 在 BA 的延长线上,AF=BC. 有如下五个结论:①AD=CD;②△ABE∽△DBC;
1
③AE×CE=BE×DE;④AB+BC= 2 BD;⑤四边形 ABCD 的面积为 AD2 ,则上列说法
2
中正确的个数为
A.2 个 B.3 个 C.4 个 D.5 个
二、填空题(每小题 4分,共 20分)
11. 点 P(-3,3)关于 y 轴对称的点 P′的坐标是 .
12. 因式分解:x3-x2-12x= .
13. 如图,按照程序计算,若输出 y 的值是 1,
则输入 x 的值是 .
(第 13 题图)
初四数学第 2 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
14. 若实数 m,n 分别满足m2 2023m 2024 0 , n2 2023n 2024 0且 m≠n,则
1 1
的值为 .
m n
15. 如图,小明同学在观察图案中“◎”“★”的排列方式时,通过研究每个图案中它们
数量的规律,发现第 n 个图案中“★”的个数是“◎”的个数的 2 倍,则 n 的值为
(第 15 题图)
三、解答题(第 16,17,18,19 题每题 10 分;第 20,21 题每题 12 分,第 22,23 题每题 13
分;满分 90 分)解答要写出必要的文字说明、证明过程或演算步骤.
16.(本题满分 10 分)
(1)先化简,再求值:(2a-1)(a-1)-(a2-3a) ,其中 a 1 2 .
4x y 3
(2)解方程组:
2x 5y 3
初四数学第 3 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
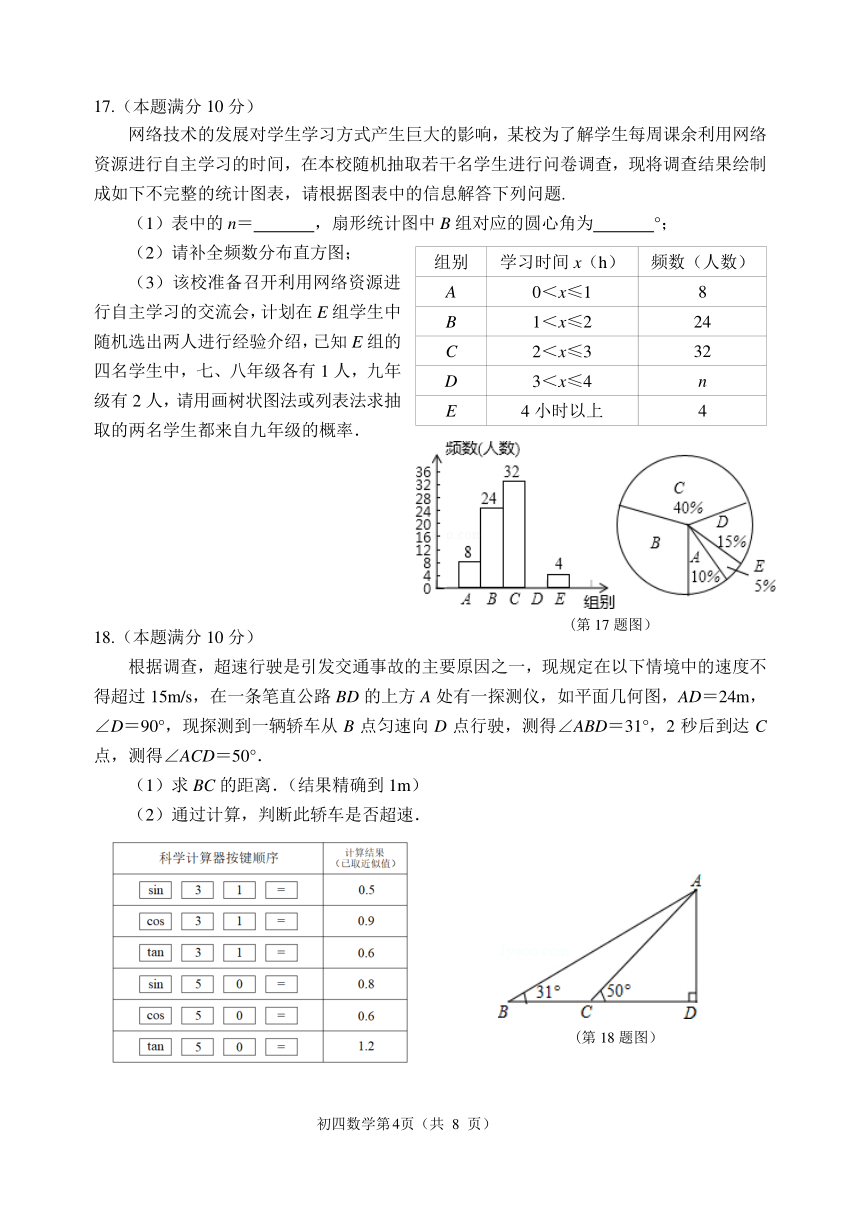
17.(本题满分 10 分)
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络
资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制
成如下不完整的统计图表,请根据图表中的信息解答下列问题.
(1)表中的 n= ,扇形统计图中 B 组对应的圆心角为 °;
(2)请补全频数分布直方图;
组别 学习时间 x(h) 频数(人数)
(3)该校准备召开利用网络资源进
A 0<x≤1 8
行自主学习的交流会,计划在 E 组学生中
B 1<x≤2 24
随机选出两人进行经验介绍,已知 E 组的
C 2<x≤3 32
四名学生中,七、八年级各有 1 人,九年
D 3<x≤4 n
级有 2 人,请用画树状图法或列表法求抽
E 4 小时以上 4
取的两名学生都来自九年级的概率.
(第 17 题图)
18.(本题满分 10 分)
根据调查,超速行驶是引发交通事故的主要原因之一,现规定在以下情境中的速度不
得超过 15m/s,在一条笔直公路 BD 的上方 A 处有一探测仪,如平面几何图,AD=24m,
∠D=90°,现探测到一辆轿车从 B 点匀速向 D 点行驶,测得∠ABD=31°,2 秒后到达 C
点,测得∠ACD=50°.
(1)求 BC 的距离.(结果精确到 1m)
(2)通过计算,判断此轿车是否超速.
(第 18 题图)
初四数学第 4 页(共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
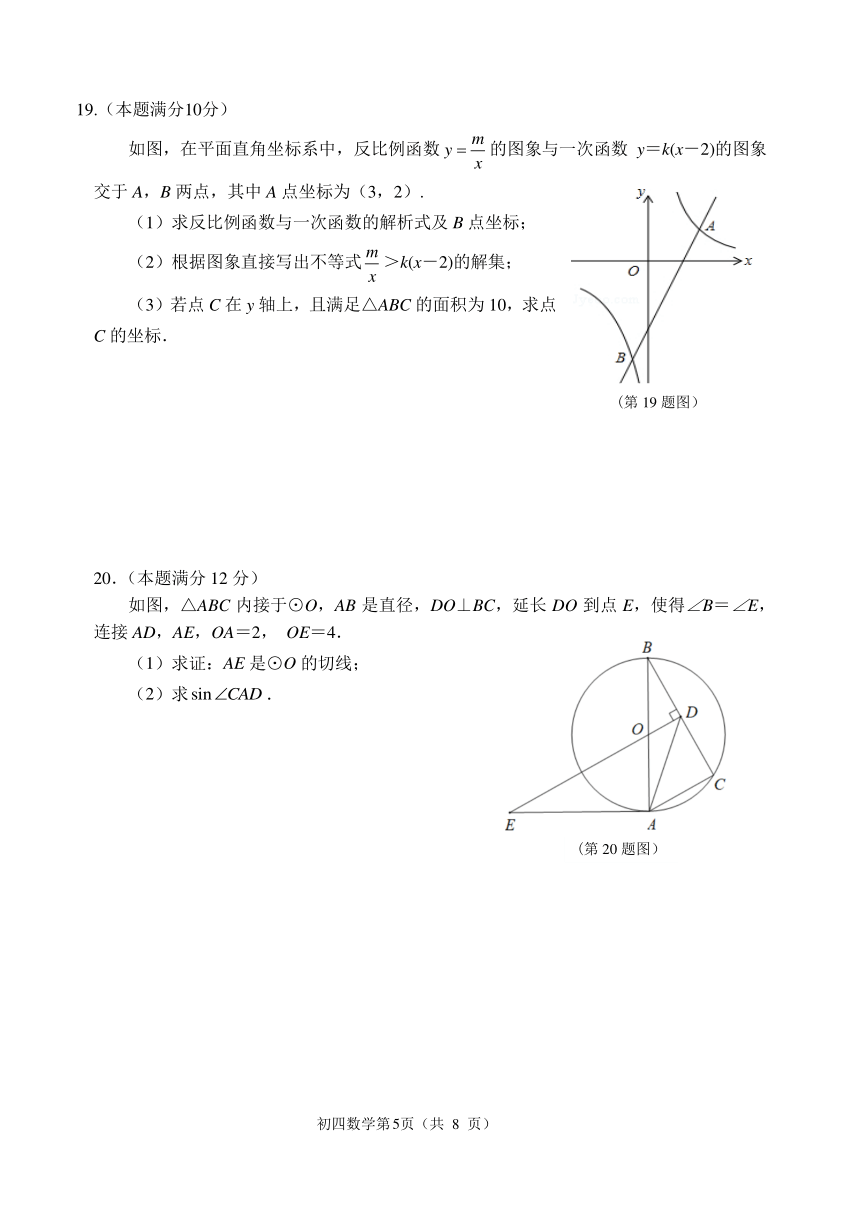
19.(本题满分10分)
m
如图,在平面直角坐标系中,反比例函数 y 的图象与一次函数 y=k(x-2)的图象
x
交于 A,B 两点,其中 A 点坐标为(3,2).
(1)求反比例函数与一次函数的解析式及 B 点坐标;
m
(2)根据图象直接写出不等式 >k(x-2)的解集;
x
(3)若点 C 在 y 轴上,且满足△ABC 的面积为 10,求点
C 的坐标.
(第 19 题图)
20.(本题满分 12 分)
如图,△ABC 内接于⊙O,AB 是直径,DO⊥BC,延长 DO 到点 E,使得∠B=∠E,
连接 AD,AE,OA=2, OE=4.
(1)求证:AE 是⊙O 的切线;
(2)求 sin CAD .
(第 20 题图)
初四数学第 5 页(共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
21.(本题满分 12 分)
如图,在以 O 为圆心,1 为半径的四分之一圆弧组成的扇形中,点 P 在弧 AB 上运动
(不与端点 A,B 重合),连接 PO,作 PQ 垂直于半径 OA,垂足为 Q,设∠POA=∠α.
(1)设 PQ 的长度为 y,y 是角 α的函数吗?请说明理由;
(2)若 Rt△POQ 的面积为 S,请回答下列问题:
①当点 P 在弧 AB 上运动时,随着角 α的逐渐变大,S 的变化规律为
(横线处填“逐渐变大”“逐渐变小”“先变大再变小”“先变小再变大”);
②求面积 S 关于角 α的表达式,并写出角 α的取值范围;
③当 S 取最大值时,请直接写出角 α的值.
(第 21 题图)
初四数学第 6 页(共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
22.(本题满分 13 分)
如图,在边长为 6 的菱形 ABCD 中,∠BCD=60°,连接 BD,点 E,F 分别是边 AB,
BC 上的动点,且 AE=BF,连接 DE,DF,EF.
(1)如图①,当点 E 是边 AB 的中点时,求∠EDF 的度数;
(2)如图②,当点 E 是边 AB 上任意一点时,∠EDF 的度数是否发生改变?若不改
变,请证明;若发生改变,请说明理由;
3
(3)若点 P 是线段 BD 上的一个动点,连接 PF,求 PF+ DP 的最小值.
2
(第 22 题图)
初四数学第 7 页(共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
23.(本题满分 13 分)
已知抛物线 y=ax2+bx-3(a≠0)与 x 轴交于点 A(-1,0),点 B(3,0),与 y 轴
交于点 C.
(1)求抛物线的表达式;
(2)如图,若直线 BC 下方的抛物线上有一动点 M,过点 M 作 y 轴平行线交 BC 于
N,过点 M 作 BC 的垂线,垂足为 H,求△HMN 周长的最大值;
(3)若点 P 在抛物线的对称轴上,点 Q 在 x 轴上,是否存在以 B,C,P,Q 为顶点
的四边形为平行四边形,若存在,求出点 Q 的坐标,若不存在,请说明理由;
(4)将抛物线向左平移 1 个单位,再向上平移 4 个单位,得到一个新的抛物线,问在
y 轴正半轴上是否存在一点 F,使得当经过点 F 的任意一条直线与新抛物线交于 S,T 两点
1 1
时,总有 为定值?若存在,求出点 F 坐标及定值,若不存在,请说明理由.
FS 2 FT 2
备用图 1 备用图 2
(第 23 题图)
初四数学第 8 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
2023—2024 学年度第二学期期中质量检测
初四数学试题参考答案
友情提示: 解题方法只要正确,可参照得分.
一、选择题(本题共 10 小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的
选项填在下面的表中.每小题 4 分,满分 40 分,错选、不选或选出的答案超过一个,均记
0 分.)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B D A C D B C
二、填空题(每小题 4 分,共 20 分)
3 2023
11. (3,3); 12. x(x-4)(x+3); 13. ; 14. ; 15. 11.
4 2024
15 题解析:∵第 n 个图案中“◎”的个数为 3n,
n(n 1)
第 n 个图案中“★”的个数为 ,
2
n(n 1)
∴由题意得: =2×3n ,解得:n=11 .
2
三、解答题(第 16,17,18,19 题每题 10 分;第 20,21 题每题 12 分,第 22,23 题每题 13
分;满分 90 分)解答要写出必要的文字说明、证明过程或演算步骤.
16.(本题满分 10 分)
解:(1)(2a-1)(a-1)-(a2-3a)
=2a2-3a+1-a2+3a
=a2+1 …….….3 分
∵ a 1 2
∴原式 a2 1 (1 2)2 1 4 2 2 …….….5 分
4x y 3①
(2)
2x 5y 3②
由①得: y 4x 3③,
把③代入②得:2x 5 4x 3 3,
解得: x 1, …….….8 分
初四数学答案第 1 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
把 x 1代入③得 y 4 1 3 1,
x 1
∴方程组的解为 …….….10 分
y 1
17.(本题满分 10 分)
解:(1)8÷10%=80,n=15%×80=12, …….….2 分
24
B 组对应的圆心角= ×360°=108°, …….….4 分
80
(2)如图所示:
(第 17 题图)
…….….6 分
(3)画树状图为:
…….….9 分
共 12 种可能,抽取的两名学生都来自九年级的有 2 种可能,
∴ 2 1P(两个学生都是九年级) ,
12 6
答:抽取的两名学生都来自九年级的概率为 1 .…….….10 分
6
18.(本题满分 10 分)
解:(1)∵在 Rt△ABD 中,AD=24m,∠B=31°,
AD 24
∴tan31°= ,即 BD= =40m, …….….3 分
BD 0.6
∵在 Rt△ACD 中,AD=24m,∠ACD=50°,
AD 24
∴tan50°= ,即 CD= =20m, …….….6 分
CD 1.2
初四数学答案第 2 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
∴BC=BD-CD=40-20=20m,
则 BC 的距离为 20m; …….….7 分
(2)根据题意得:20÷2=10m/s<15m/s,
∴此轿车没有超速. …….….10 分
19.(本题满分 10 分)
m
解:(1)∵点 A(3,2)在反比例函数 y ,和一次函数 y=k(x-2)上;
x
m
∴ 2 ,2=k(3-2),解得 m=6,k=2;
3
6
∴反比例函数的解析式为 y= , …….….1 分
x
∴一次函数的解析式为 y=2x-4; …….….2 分
∵点 B 是一次函数与反比例函数的另一个交点,
6
∴ =2x-4,解得 x1=3,x2=-1;
x
∴B 点的坐标为(-1,-6); …….….3 分
(2)x<-1 或 0<x<3; …….….5 分 (第 19 题图)
(3)设 y=2x-4 与 y 轴的交点为 M,则点 M 的坐标为(0,-4),
设 C 点的坐标为(0,yc),
1
由题意知 ×3×|yc-(-4)|+ ×1×|yc-(-4)|=10, …….….7 分
2
解得|yc+4|=5,
当 yc+4≥0 时,yc+4=5,解得 yc=1,
当 yc+4≤0 时,yc+4=-5,解得 yc=-9,
∴点 C 的坐标为(0,1)或(0,-9). …….….10 分
20.(本题满分 12 分)
解:(1)∵在△ODB 和△OAE 中
B E , DOB AOE ,
∴△ODB ∽△OAE, …….….2 分
∴ OAE ODB,
∵OD⊥BC,
∴ ODB 90 ,
∴ OAE 90
∴AE 是⊙O 的切线; …….….4 分
(2)由第(1)问知△ODB ∽△OAE, (第 20 题图)
初四数学答案第 3 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
OD OB OD 2
∴ ,即 ,
OA OE 2 4
∴OD=1, …….….6 分
在 Rt△ODB 中,由勾股定理得:OD2 DB2 OB2 ,
∴ DB OB2 OD2 22 12 3 .
∵ OD⊥BC,OD 经过⊙O 的圆心,
∴CD DB 3 , …….….9 分
∵O,D 分别是 AB,BC 的中点,
∴AC=2OD=2,
2
∴在 Rt△ACD 中, AD AC2 CD2 22 3 7 ,…….….11 分
CD 3 21
∴ sin CAD . …….….12 分
AD 7 7
21.(本题满分 12 分)
解:(1)是.
∵对于变量 α 的每一个值,PQ 的长度 y 都有唯一确定的值与之对应,
∴y 是 α 的函数; …….….3 分
(2)①先变大再变小 …….….5 分
②在 Rt△POQ 中,
∵OQ=OP cosα=cosα , PQ=OP sinα=sinα ;
1 1
∴S= OQ PQ= cos sin ; …….….8 分
2 2
0°<∠α<90°; …….….10 分 (第 21 题图)
③当 S 取最大值时,∠α=45°. …….….12 分
理由:设点 C 为 OP 的中点,连结 QC,过点 Q 作 OP 的垂线,垂足为 H,连结
QH.
∵点 C 为 OP 的中点,PQ⊥OQ
∴OC=CQ
1 1
∵S= PO HQ≤ PO CQ
2 2
∴当点 P 运动到弧 AB 的中点,使得 HQ 与 CQ 重合时,S 的值最大
此时,HQ=HO,HQ⊥OH,
∴△OHQ 为等腰直角三角形。
初四数学答案第 4 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
∴∠α=45°.
22.(本题满分 13 分)
解:(1)∵四边形 ABCD 是菱形,边长为 6,
∴AB=BC=CD=AD=6, ∠BCD=∠BAD=60°,
∴△ABD,△BCD 是等边三角形, …….….2 分
∵点 E 是边 AB 的中点,AE=BF,
∴点 F 是边 BC 的中点,
∴∠ADE=∠BDE=∠BDF=∠CDF=30°,
∴∠EDF=∠BDE+∠BDF=60°; …….….4 分
(2)∠EDF 的度数不改变,
证明:△ABD,△BCD 是等边三角形,
∴AD=BD,∠DAB=∠DBC=60°,
∵AE=BF,
∴△ADE≌△BDF(SAS), …….….6 分
∴∠ADE=∠BDF,
∴∠EDF=∠ADB=60°; …….….8 分
(3)如图,过点 P 作 PG⊥AD 于点 G,连接 PF,过点 F 作 FG′⊥AD 于点 G′,交 BD 于
点 P′,
∵∠ADB=60°,
3
∴GP=DP sin60°= DP,
2
3
∴PF+ DP= PF+GP, …….….10 分
2
∴当点 F,P,G 三点共线,且 FG⊥AD 时,PF+GP 有最小值,最小值为 FG′的长,
过点 D 作 DH⊥BC 于点 H,
∵四边形 ABCD 是菱形,
∴DH= FG′,
3
∴PF+ DP 的最小值即为 DH 的长,
2
∵DH⊥BC,△BDC 是等边三角形,
∴DH= CD sin60°= 3 3 ,
(第 22 题图)
3
∴PF+ DP 的最小值为3 3 . …….….13 分
2
23.(本题满分 13 分)
初四数学答案第 5 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
解:(1)∵A(-1,0),B(3,0)在抛物线 y ax2 bx 3(a≠0)上,
a b 3 0
∴
9a 3b 3 0
a 1
解得:
b 2
∴抛物线的表达式为:y=x2-2x-3; …….….3 分
(2)∵抛物线的表达式为:y=x2-2x-3
∴C(0,-3)
设直线 BC 的解析式为 y=kx+n,
∵B(3,0),C(0,-3)
3k n 0 k 1
∴ 解得:
n 3 n 3
∴直线 BC 的解析式为 y=x-3 …….….4 分
设 M(m,m2 2m 3),其中 0<m<3,
则 N(m,m-3)
MN=m-3-(m2 2m 3)= m2 3m
∵OB=OC=3
∴∠OCB=45°
∵MN∥y 轴
∴∠MNH=∠OCB=45°
2
∴ HM HN MN …….….5 分
2
2 2
∴△HMN 的周长 l=( 1)MN
2 2
= ( 2 1)( m2 3m)
= ( 2 1)m2 3( 2 1)m
3 9 2 9
当m 时, l …….….6 分
2 最大值 4
(3)存在
由题意知,抛物线的对称轴为直线 x 1,
初四数学答案第 6 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
B(3,0),C(0,-3)
设点 P 坐标为(1,s),点 Q 坐标为(t,0)
①当 BC 为对角线时,
3 0 1 t
0 3 s 0
s 3
∴
t 2
(第 23 题图)
∴Q(2,0) …….….7 分
②当 BP 为对角线时,
3 1 0 t
0 s 3 0
s 3
∴
t 4
∴Q(4,0) …….….8 分 (第 23 题图)
③当 BQ 为对角线时,
3 t 1 0
0 0 s 3
s 3
∴
t 2
∴Q(-2,0) …….….9 分
(第 23 题图)
综上所述,Q 点的坐标为(2,0),(4,0),(-2,0)
(4)当抛物线 y=x2-2x-3 向左平移 1 个单位,向上平移 4 个单位后,得到新的抛物线
y=(x+1)2-2(x+1)-3+4,即 y=x2 …….….10 分
设 ST 的解析式为 y=kx+b,点 S 坐标为(x1,y1),点 T 坐标为(x2,y2),则 F(0,b)
y kx b
y x
2
∴ x2 kx b 0
∴ x1 x2 k , x1x2 b
初四数学答案第 7 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
FS 2 x 21 (y1 b)
2 x 21 k
2x 21 (1 k
2 )x 21 …….….11 分
同理, FT 2 (1 k 2 )x 22
2
1 1 1 1 1 1 (x1 x2 ) 2x
2
1x2 1 k 2b
∴ ( ) [ ] ( ) ….….12
FS2 FT 2 1 k2 x2 2 2
分
1 x2 1 k (x1x )
2
2 1 k
2 b2
1 1 1
当b 时, 4
2 FS2 FT 2
1 1 1
∴定点 F(0, ), 的值为 4. …….….13 分
2 FS 2 FT 2
初四数学答案第 8 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
初 四 数 学 试 题
本试卷共 8 页,满分 150 分,考试时间 120 分钟.考试结束后。
注意事项:
1.答题前,考生务必用 0.5 毫米黑色签字笔将学校、班级、姓名、考试号、座号填写
在答题卡和试卷规定位置。
2. 选择题每小题选出答案后,用 2B 铅笔涂黑答题卡对应题目的答案标号;如需改
动,用橡皮擦干净后,再选涂其他答案标号。
3.非选择题必须用 0.5 毫米黑色签字笔作答,字体工整、笔迹清晰,写在答题卡各题
目指定区域内;如需改动,先划掉原来答案,然后再写上新答案。严禁使用涂改液、胶带
纸、修正带修改。
4.保证答题卡清洁、完整,严禁折叠,严禁在答题卡上做任何标记。
5.评分以答题卡上的答案为依据。不按以上要求作答的答案无效。
一、 选择题(本题共 10 小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确
的选项填在下面的表中.每小题 4 分, 满分 40 分,错选、不选、多选,均记 0 分.)
1. 某体育场有 10000 个座位,10000 用科学记数法表示为
A.1×104 B. 0.1×105 C.10×104 D.10×103
2.下列几何图形中,是轴对称图形但不是中心对称图形的有
A.4 个
B.3 个
C.2 个
D.1 个
下列运算正确的是 (第 2 题图) 3.
A.a a2=a3 B.3a-a=3 C.a4÷a3=a2 D.(a3)2=a5
4. 一组数据 3,3,4,6,8,9 的中位数是
A.4 B.5 C.5.5 D.6
x 3 0
5. 不等式组 的解集在数轴上表示正确的是
2x 4 0
A. B.
C. D.
6.如图,直线 a∥b,若∠1=24°,∠A=46°,则∠2 的度数为
A.70° B.46° C.40° D.30° (第 6 题图)
初四数学第 1 页(共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
k
7. 设点 A(x1,y1)和点 B(x2,y2)是反比例函数 y 图象上的两点,当 x1<x2<0 时,
x
y1>y2,则一次函数 y=-2x+k 的图象不经过的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.甲、乙两人沿着总长度为 10km 的“健身步道”健步走,甲的速度是乙的 1.2 倍,甲比乙
提前 12 分钟走完全程.设乙的速度为 x km/h,则下列方程中正确的是
10 10 10 10 10 10 10 10
A. 12 B. 0.2 C. 12 D. 0.2
x 1.2x 1.2x x 1.2x x x 1.2x
9.如图,将矩形纸片 ABCD 折叠,使点 B 与点 D 重合,折痕为 MN,若 AB=2,BC=4,
那么线段 MN 的长为
2 5 4 5
A. B. 5 C. D. 2 5
5 5
(第 9 题图) (第 10 题图)
10.如图,四边形 ABCD 内接于⊙O,AC 为直径,∠ABC 的平分线 BD 交 AC 于点 E,
点 F 在 BA 的延长线上,AF=BC. 有如下五个结论:①AD=CD;②△ABE∽△DBC;
1
③AE×CE=BE×DE;④AB+BC= 2 BD;⑤四边形 ABCD 的面积为 AD2 ,则上列说法
2
中正确的个数为
A.2 个 B.3 个 C.4 个 D.5 个
二、填空题(每小题 4分,共 20分)
11. 点 P(-3,3)关于 y 轴对称的点 P′的坐标是 .
12. 因式分解:x3-x2-12x= .
13. 如图,按照程序计算,若输出 y 的值是 1,
则输入 x 的值是 .
(第 13 题图)
初四数学第 2 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
14. 若实数 m,n 分别满足m2 2023m 2024 0 , n2 2023n 2024 0且 m≠n,则
1 1
的值为 .
m n
15. 如图,小明同学在观察图案中“◎”“★”的排列方式时,通过研究每个图案中它们
数量的规律,发现第 n 个图案中“★”的个数是“◎”的个数的 2 倍,则 n 的值为
(第 15 题图)
三、解答题(第 16,17,18,19 题每题 10 分;第 20,21 题每题 12 分,第 22,23 题每题 13
分;满分 90 分)解答要写出必要的文字说明、证明过程或演算步骤.
16.(本题满分 10 分)
(1)先化简,再求值:(2a-1)(a-1)-(a2-3a) ,其中 a 1 2 .
4x y 3
(2)解方程组:
2x 5y 3
初四数学第 3 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
17.(本题满分 10 分)
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络
资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制
成如下不完整的统计图表,请根据图表中的信息解答下列问题.
(1)表中的 n= ,扇形统计图中 B 组对应的圆心角为 °;
(2)请补全频数分布直方图;
组别 学习时间 x(h) 频数(人数)
(3)该校准备召开利用网络资源进
A 0<x≤1 8
行自主学习的交流会,计划在 E 组学生中
B 1<x≤2 24
随机选出两人进行经验介绍,已知 E 组的
C 2<x≤3 32
四名学生中,七、八年级各有 1 人,九年
D 3<x≤4 n
级有 2 人,请用画树状图法或列表法求抽
E 4 小时以上 4
取的两名学生都来自九年级的概率.
(第 17 题图)
18.(本题满分 10 分)
根据调查,超速行驶是引发交通事故的主要原因之一,现规定在以下情境中的速度不
得超过 15m/s,在一条笔直公路 BD 的上方 A 处有一探测仪,如平面几何图,AD=24m,
∠D=90°,现探测到一辆轿车从 B 点匀速向 D 点行驶,测得∠ABD=31°,2 秒后到达 C
点,测得∠ACD=50°.
(1)求 BC 的距离.(结果精确到 1m)
(2)通过计算,判断此轿车是否超速.
(第 18 题图)
初四数学第 4 页(共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
19.(本题满分10分)
m
如图,在平面直角坐标系中,反比例函数 y 的图象与一次函数 y=k(x-2)的图象
x
交于 A,B 两点,其中 A 点坐标为(3,2).
(1)求反比例函数与一次函数的解析式及 B 点坐标;
m
(2)根据图象直接写出不等式 >k(x-2)的解集;
x
(3)若点 C 在 y 轴上,且满足△ABC 的面积为 10,求点
C 的坐标.
(第 19 题图)
20.(本题满分 12 分)
如图,△ABC 内接于⊙O,AB 是直径,DO⊥BC,延长 DO 到点 E,使得∠B=∠E,
连接 AD,AE,OA=2, OE=4.
(1)求证:AE 是⊙O 的切线;
(2)求 sin CAD .
(第 20 题图)
初四数学第 5 页(共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
21.(本题满分 12 分)
如图,在以 O 为圆心,1 为半径的四分之一圆弧组成的扇形中,点 P 在弧 AB 上运动
(不与端点 A,B 重合),连接 PO,作 PQ 垂直于半径 OA,垂足为 Q,设∠POA=∠α.
(1)设 PQ 的长度为 y,y 是角 α的函数吗?请说明理由;
(2)若 Rt△POQ 的面积为 S,请回答下列问题:
①当点 P 在弧 AB 上运动时,随着角 α的逐渐变大,S 的变化规律为
(横线处填“逐渐变大”“逐渐变小”“先变大再变小”“先变小再变大”);
②求面积 S 关于角 α的表达式,并写出角 α的取值范围;
③当 S 取最大值时,请直接写出角 α的值.
(第 21 题图)
初四数学第 6 页(共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
22.(本题满分 13 分)
如图,在边长为 6 的菱形 ABCD 中,∠BCD=60°,连接 BD,点 E,F 分别是边 AB,
BC 上的动点,且 AE=BF,连接 DE,DF,EF.
(1)如图①,当点 E 是边 AB 的中点时,求∠EDF 的度数;
(2)如图②,当点 E 是边 AB 上任意一点时,∠EDF 的度数是否发生改变?若不改
变,请证明;若发生改变,请说明理由;
3
(3)若点 P 是线段 BD 上的一个动点,连接 PF,求 PF+ DP 的最小值.
2
(第 22 题图)
初四数学第 7 页(共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
23.(本题满分 13 分)
已知抛物线 y=ax2+bx-3(a≠0)与 x 轴交于点 A(-1,0),点 B(3,0),与 y 轴
交于点 C.
(1)求抛物线的表达式;
(2)如图,若直线 BC 下方的抛物线上有一动点 M,过点 M 作 y 轴平行线交 BC 于
N,过点 M 作 BC 的垂线,垂足为 H,求△HMN 周长的最大值;
(3)若点 P 在抛物线的对称轴上,点 Q 在 x 轴上,是否存在以 B,C,P,Q 为顶点
的四边形为平行四边形,若存在,求出点 Q 的坐标,若不存在,请说明理由;
(4)将抛物线向左平移 1 个单位,再向上平移 4 个单位,得到一个新的抛物线,问在
y 轴正半轴上是否存在一点 F,使得当经过点 F 的任意一条直线与新抛物线交于 S,T 两点
1 1
时,总有 为定值?若存在,求出点 F 坐标及定值,若不存在,请说明理由.
FS 2 FT 2
备用图 1 备用图 2
(第 23 题图)
初四数学第 8 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
2023—2024 学年度第二学期期中质量检测
初四数学试题参考答案
友情提示: 解题方法只要正确,可参照得分.
一、选择题(本题共 10 小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的
选项填在下面的表中.每小题 4 分,满分 40 分,错选、不选或选出的答案超过一个,均记
0 分.)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B D A C D B C
二、填空题(每小题 4 分,共 20 分)
3 2023
11. (3,3); 12. x(x-4)(x+3); 13. ; 14. ; 15. 11.
4 2024
15 题解析:∵第 n 个图案中“◎”的个数为 3n,
n(n 1)
第 n 个图案中“★”的个数为 ,
2
n(n 1)
∴由题意得: =2×3n ,解得:n=11 .
2
三、解答题(第 16,17,18,19 题每题 10 分;第 20,21 题每题 12 分,第 22,23 题每题 13
分;满分 90 分)解答要写出必要的文字说明、证明过程或演算步骤.
16.(本题满分 10 分)
解:(1)(2a-1)(a-1)-(a2-3a)
=2a2-3a+1-a2+3a
=a2+1 …….….3 分
∵ a 1 2
∴原式 a2 1 (1 2)2 1 4 2 2 …….….5 分
4x y 3①
(2)
2x 5y 3②
由①得: y 4x 3③,
把③代入②得:2x 5 4x 3 3,
解得: x 1, …….….8 分
初四数学答案第 1 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
把 x 1代入③得 y 4 1 3 1,
x 1
∴方程组的解为 …….….10 分
y 1
17.(本题满分 10 分)
解:(1)8÷10%=80,n=15%×80=12, …….….2 分
24
B 组对应的圆心角= ×360°=108°, …….….4 分
80
(2)如图所示:
(第 17 题图)
…….….6 分
(3)画树状图为:
…….….9 分
共 12 种可能,抽取的两名学生都来自九年级的有 2 种可能,
∴ 2 1P(两个学生都是九年级) ,
12 6
答:抽取的两名学生都来自九年级的概率为 1 .…….….10 分
6
18.(本题满分 10 分)
解:(1)∵在 Rt△ABD 中,AD=24m,∠B=31°,
AD 24
∴tan31°= ,即 BD= =40m, …….….3 分
BD 0.6
∵在 Rt△ACD 中,AD=24m,∠ACD=50°,
AD 24
∴tan50°= ,即 CD= =20m, …….….6 分
CD 1.2
初四数学答案第 2 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
∴BC=BD-CD=40-20=20m,
则 BC 的距离为 20m; …….….7 分
(2)根据题意得:20÷2=10m/s<15m/s,
∴此轿车没有超速. …….….10 分
19.(本题满分 10 分)
m
解:(1)∵点 A(3,2)在反比例函数 y ,和一次函数 y=k(x-2)上;
x
m
∴ 2 ,2=k(3-2),解得 m=6,k=2;
3
6
∴反比例函数的解析式为 y= , …….….1 分
x
∴一次函数的解析式为 y=2x-4; …….….2 分
∵点 B 是一次函数与反比例函数的另一个交点,
6
∴ =2x-4,解得 x1=3,x2=-1;
x
∴B 点的坐标为(-1,-6); …….….3 分
(2)x<-1 或 0<x<3; …….….5 分 (第 19 题图)
(3)设 y=2x-4 与 y 轴的交点为 M,则点 M 的坐标为(0,-4),
设 C 点的坐标为(0,yc),
1
由题意知 ×3×|yc-(-4)|+ ×1×|yc-(-4)|=10, …….….7 分
2
解得|yc+4|=5,
当 yc+4≥0 时,yc+4=5,解得 yc=1,
当 yc+4≤0 时,yc+4=-5,解得 yc=-9,
∴点 C 的坐标为(0,1)或(0,-9). …….….10 分
20.(本题满分 12 分)
解:(1)∵在△ODB 和△OAE 中
B E , DOB AOE ,
∴△ODB ∽△OAE, …….….2 分
∴ OAE ODB,
∵OD⊥BC,
∴ ODB 90 ,
∴ OAE 90
∴AE 是⊙O 的切线; …….….4 分
(2)由第(1)问知△ODB ∽△OAE, (第 20 题图)
初四数学答案第 3 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
OD OB OD 2
∴ ,即 ,
OA OE 2 4
∴OD=1, …….….6 分
在 Rt△ODB 中,由勾股定理得:OD2 DB2 OB2 ,
∴ DB OB2 OD2 22 12 3 .
∵ OD⊥BC,OD 经过⊙O 的圆心,
∴CD DB 3 , …….….9 分
∵O,D 分别是 AB,BC 的中点,
∴AC=2OD=2,
2
∴在 Rt△ACD 中, AD AC2 CD2 22 3 7 ,…….….11 分
CD 3 21
∴ sin CAD . …….….12 分
AD 7 7
21.(本题满分 12 分)
解:(1)是.
∵对于变量 α 的每一个值,PQ 的长度 y 都有唯一确定的值与之对应,
∴y 是 α 的函数; …….….3 分
(2)①先变大再变小 …….….5 分
②在 Rt△POQ 中,
∵OQ=OP cosα=cosα , PQ=OP sinα=sinα ;
1 1
∴S= OQ PQ= cos sin ; …….….8 分
2 2
0°<∠α<90°; …….….10 分 (第 21 题图)
③当 S 取最大值时,∠α=45°. …….….12 分
理由:设点 C 为 OP 的中点,连结 QC,过点 Q 作 OP 的垂线,垂足为 H,连结
QH.
∵点 C 为 OP 的中点,PQ⊥OQ
∴OC=CQ
1 1
∵S= PO HQ≤ PO CQ
2 2
∴当点 P 运动到弧 AB 的中点,使得 HQ 与 CQ 重合时,S 的值最大
此时,HQ=HO,HQ⊥OH,
∴△OHQ 为等腰直角三角形。
初四数学答案第 4 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
∴∠α=45°.
22.(本题满分 13 分)
解:(1)∵四边形 ABCD 是菱形,边长为 6,
∴AB=BC=CD=AD=6, ∠BCD=∠BAD=60°,
∴△ABD,△BCD 是等边三角形, …….….2 分
∵点 E 是边 AB 的中点,AE=BF,
∴点 F 是边 BC 的中点,
∴∠ADE=∠BDE=∠BDF=∠CDF=30°,
∴∠EDF=∠BDE+∠BDF=60°; …….….4 分
(2)∠EDF 的度数不改变,
证明:△ABD,△BCD 是等边三角形,
∴AD=BD,∠DAB=∠DBC=60°,
∵AE=BF,
∴△ADE≌△BDF(SAS), …….….6 分
∴∠ADE=∠BDF,
∴∠EDF=∠ADB=60°; …….….8 分
(3)如图,过点 P 作 PG⊥AD 于点 G,连接 PF,过点 F 作 FG′⊥AD 于点 G′,交 BD 于
点 P′,
∵∠ADB=60°,
3
∴GP=DP sin60°= DP,
2
3
∴PF+ DP= PF+GP, …….….10 分
2
∴当点 F,P,G 三点共线,且 FG⊥AD 时,PF+GP 有最小值,最小值为 FG′的长,
过点 D 作 DH⊥BC 于点 H,
∵四边形 ABCD 是菱形,
∴DH= FG′,
3
∴PF+ DP 的最小值即为 DH 的长,
2
∵DH⊥BC,△BDC 是等边三角形,
∴DH= CD sin60°= 3 3 ,
(第 22 题图)
3
∴PF+ DP 的最小值为3 3 . …….….13 分
2
23.(本题满分 13 分)
初四数学答案第 5 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
解:(1)∵A(-1,0),B(3,0)在抛物线 y ax2 bx 3(a≠0)上,
a b 3 0
∴
9a 3b 3 0
a 1
解得:
b 2
∴抛物线的表达式为:y=x2-2x-3; …….….3 分
(2)∵抛物线的表达式为:y=x2-2x-3
∴C(0,-3)
设直线 BC 的解析式为 y=kx+n,
∵B(3,0),C(0,-3)
3k n 0 k 1
∴ 解得:
n 3 n 3
∴直线 BC 的解析式为 y=x-3 …….….4 分
设 M(m,m2 2m 3),其中 0<m<3,
则 N(m,m-3)
MN=m-3-(m2 2m 3)= m2 3m
∵OB=OC=3
∴∠OCB=45°
∵MN∥y 轴
∴∠MNH=∠OCB=45°
2
∴ HM HN MN …….….5 分
2
2 2
∴△HMN 的周长 l=( 1)MN
2 2
= ( 2 1)( m2 3m)
= ( 2 1)m2 3( 2 1)m
3 9 2 9
当m 时, l …….….6 分
2 最大值 4
(3)存在
由题意知,抛物线的对称轴为直线 x 1,
初四数学答案第 6 页 (共 8 页)
{#{QQABBDQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
B(3,0),C(0,-3)
设点 P 坐标为(1,s),点 Q 坐标为(t,0)
①当 BC 为对角线时,
3 0 1 t
0 3 s 0
s 3
∴
t 2
(第 23 题图)
∴Q(2,0) …….….7 分
②当 BP 为对角线时,
3 1 0 t
0 s 3 0
s 3
∴
t 4
∴Q(4,0) …….….8 分 (第 23 题图)
③当 BQ 为对角线时,
3 t 1 0
0 0 s 3
s 3
∴
t 2
∴Q(-2,0) …….….9 分
(第 23 题图)
综上所述,Q 点的坐标为(2,0),(4,0),(-2,0)
(4)当抛物线 y=x2-2x-3 向左平移 1 个单位,向上平移 4 个单位后,得到新的抛物线
y=(x+1)2-2(x+1)-3+4,即 y=x2 …….….10 分
设 ST 的解析式为 y=kx+b,点 S 坐标为(x1,y1),点 T 坐标为(x2,y2),则 F(0,b)
y kx b
y x
2
∴ x2 kx b 0
∴ x1 x2 k , x1x2 b
初四数学答案第 7 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
FS 2 x 21 (y1 b)
2 x 21 k
2x 21 (1 k
2 )x 21 …….….11 分
同理, FT 2 (1 k 2 )x 22
2
1 1 1 1 1 1 (x1 x2 ) 2x
2
1x2 1 k 2b
∴ ( ) [ ] ( ) ….….12
FS2 FT 2 1 k2 x2 2 2
分
1 x2 1 k (x1x )
2
2 1 k
2 b2
1 1 1
当b 时, 4
2 FS2 FT 2
1 1 1
∴定点 F(0, ), 的值为 4. …….….13 分
2 FS 2 FT 2
初四数学答案第 8 页 (共 8 页)
{#{QQABDBQSU4wgggiwAkAJIaIAACRBg5CrAAQQ1kmCCUEuCQkkIAGCjJCACoEIoAGQAAAHAuMAowAjyAJBFSAABFIA=B}A#A} =}#}
同课章节目录
