2023-2024学年苏科版九年级数学下册期中复习模拟卷(无答案)
文档属性
| 名称 | 2023-2024学年苏科版九年级数学下册期中复习模拟卷(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 660.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 00:00:00 | ||
图片预览



文档简介
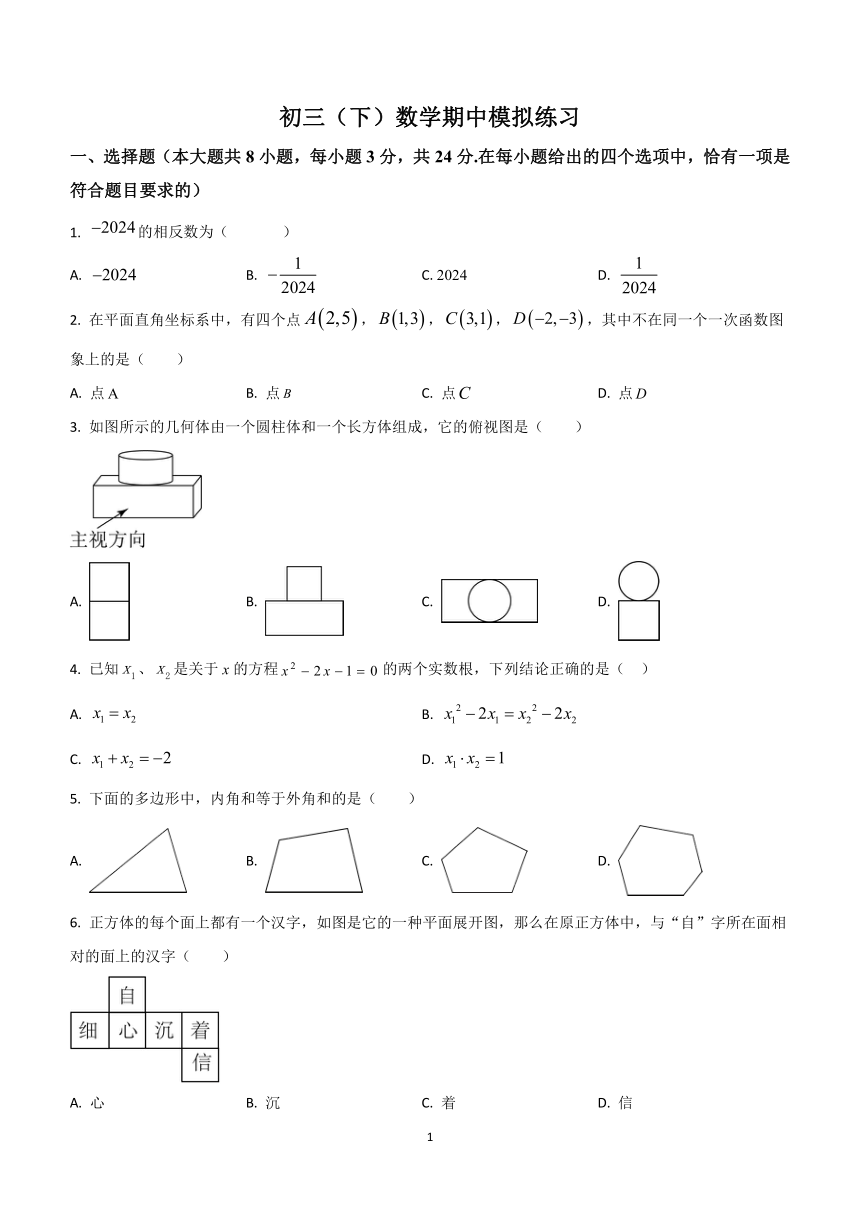
初三(下)数学期中模拟练习
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有一项是符合题目要求的)
1. 的相反数为( )
A. B. C. 2024 D.
2. 在平面直角坐标系中,有四个点,,,,其中不在同一个一次函数图象上的是( )
A. 点 B. 点 C. 点 D. 点
3. 如图所示的几何体由一个圆柱体和一个长方体组成,它的俯视图是( )
A. B. C. D.
4. 已知、是关于x的方程的两个实数根,下列结论正确的是( )
A. B.
C. D.
5. 下面的多边形中,内角和等于外角和的是( )
A. B. C. D.
6. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“自”字所在面相对的面上的汉字( )
A. 心 B. 沉 C. 着 D. 信
7. 在5次英语听说机考模拟练习中,甲、乙两名学生的成绩(单位:分)如下:
甲 32 37 40 34 37
乙 36 35 37 35 37
若要比较两名学生5次模拟练习成绩谁比较稳定,则选用统计量及成绩比较稳定的学生分别是( )
A. 众数,甲 B. 众数,乙 C. 方差,甲 D. 方差,乙
8. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段,和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点,则直线的“理想矩形”的面积为( )
A 12 B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
9. 若代数式有意义,则实数x的取值范围是__________.
10. 因式分解:_________.
11. 化学元素钌()是除铁()、钻()镍()以外,在室温下具有独特磁性的第四个元素.钌()的原子半径为,用科学记数法表示为________.
12. “盐城马拉松”的赛事共有三项,“马拉松” 、“半程马拉松”和“迷你健身跑”.乐乐参加了志 愿者服务工作,为估算“半程马拉松”的人数,对部分参赛选手作了调查:
调查人数 20 50 100 200 500 2000
参加人数 7 20 39 83 209 822
频率 0.350 0.400 0.390 0.415 0.418 0.411
请估算本次赛事参加“半程马拉松”人数的概率为 __________ .(精确到 0.01)
13. 如图,正方形ABCD的边长为6,分别以A,B为圆心,6为半径画弧BD,弧AC,则图中阴影部分的面积为__________________.
14. 在五个完全相同小球上分别写上1,2,3,4,5五个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从口袋中取出一个球记下数字后作为点P的纵坐标y.则在坐标平面内,点P(x,y)落在直线 y=﹣x+5上的概率是_____.
15. 在菱形中,,,的两边分别交边、于点E、F,且,记的外心为点P,则P、C两点间的最小距离为_____________.
16. 如图,在矩形ABCD中,,,点E从点A出发,沿射线AC以1cm/s的速度匀速移动.连接DE,过点E作,EF与射线BC相交于点F,作矩形DEFG,连接EG.设点E移动的时间为t(s),若EG与矩形ABCD的边平行,则t的值是______s.
三、解答题(本大题共11小题,共102分.解答时应写出文字说明、证明过程或演算步骤)
17. 计算:.
18. 先化简,再求值:,其中.
19. 已知关于x的一元二次方程有实数根.
(1)求k的取值范围.
(2)若方程有一个根为1,求方程的另一个根.
20. 如图,为边的中点,交的延长线于点,连接,平分,求证:四边形为菱形.
21. 如图,直线l1:y=kx+b与双曲线y=(x>0)交于A,B两点,与x轴交于点C,与y轴交于点E,已知点A(1,3),点C(4,0).
(1)求直线l1和双曲线的解析式;
(2)将△OCE沿直线l1翻折,点O落在第一象限内的点H处,求点H的坐标;
(3)如图,过点E作直线l2:y=3x+4交x轴负半轴于点F,在直线l2上是否存在点P,使得S△PBC=S△OBC?若存在,请直接写出所有符合条件的点P的坐标;如果不存在,请说明理由.
22. 如图,△ABC为⊙O的内接三角形,BC为⊙O的直径,在线段OC上取点D(不与端点重合),作DG⊥BC,分别交AC、圆周于E、F,连接AG,已知AG=EG.
(1)求证:AG为⊙O的切线;
(2)已知AG=2,填空:
①当四边形ABOF是菱形时,∠AEG= °;
②若OC=2DC,△AGE为等腰直角三角形,则AB= .
23. 一辆快车从甲地出发驶向乙地,在到达乙地后,立即按原路原速返回到甲地,快车出发一段时间后一辆慢车从甲地驶向乙地,中途因故停车后,继续按原速驶向乙地,两车距甲地路程与慢车行驶时间之间的函数图象如图所示,请结合图象解答下列问题:
(1)甲乙两地相距 ,快车行驶速度是 ,图中括号内的数值是 ;
(2)求快车从乙地返回甲地的过程中,y与x的函数解析式;
(3)慢车出发多长时间,两车相距.
24. 对于任意一个四位数m,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数m为“共生数”例如:,因为,所以3507是“共生数”:,因为,所以4135不是“共生数”;
(1)判断5313,6437是否为“共生数”?并说明理由;
(2)对于“共生数”n,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记.求满足各数位上的数字之和是偶数的所有n.
25. 【问题提出】如图1,用“圆规和无刻度的直尺”,作两条以为圆心的圆弧将已知扇形的面积三等分.
【问题联思】如图2,已知线段,请你用“圆规和无刻度的直尺”作一个以为底边,底角为的等腰三角形,并写出与的数量关系;
【问题再现】如图3,已知扇形,请你用“圆规和无刻度的直尺”作两条以点为圆心的圆弧,使扇形的面积被两条圆弧三等分.(友情提醒:保留作图痕迹,并用黑笔描线加深)
26. 在平面直角坐标系中,已知点A在y轴正半轴上.
(1)如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.
①________;
②如图1,已知菱形的顶点B、C、D在该二次函数的图象上,且轴,求菱形的边长;
③如图2,已知正方形的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究是否为定值.如果是,求出这个值;如果不是,请说明理由.
(2)已知正方形的顶点B、D在二次函数(a为常数,且)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.
27. (1)如图1,在矩形中,为边上一点,连接,若,过C作交于点F,
①求证:;
②若时,则 .
(2)如图2,在菱形中,,过作交的延长线于点,过作交于点,若时,求的值.
(3)如图3,在平行四边形中,,,,点E在上,且,点为上一点,连接,过作交平行四边形的边于点,若时,请直接写出的长.
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有一项是符合题目要求的)
1. 的相反数为( )
A. B. C. 2024 D.
2. 在平面直角坐标系中,有四个点,,,,其中不在同一个一次函数图象上的是( )
A. 点 B. 点 C. 点 D. 点
3. 如图所示的几何体由一个圆柱体和一个长方体组成,它的俯视图是( )
A. B. C. D.
4. 已知、是关于x的方程的两个实数根,下列结论正确的是( )
A. B.
C. D.
5. 下面的多边形中,内角和等于外角和的是( )
A. B. C. D.
6. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“自”字所在面相对的面上的汉字( )
A. 心 B. 沉 C. 着 D. 信
7. 在5次英语听说机考模拟练习中,甲、乙两名学生的成绩(单位:分)如下:
甲 32 37 40 34 37
乙 36 35 37 35 37
若要比较两名学生5次模拟练习成绩谁比较稳定,则选用统计量及成绩比较稳定的学生分别是( )
A. 众数,甲 B. 众数,乙 C. 方差,甲 D. 方差,乙
8. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段,和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点,则直线的“理想矩形”的面积为( )
A 12 B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
9. 若代数式有意义,则实数x的取值范围是__________.
10. 因式分解:_________.
11. 化学元素钌()是除铁()、钻()镍()以外,在室温下具有独特磁性的第四个元素.钌()的原子半径为,用科学记数法表示为________.
12. “盐城马拉松”的赛事共有三项,“马拉松” 、“半程马拉松”和“迷你健身跑”.乐乐参加了志 愿者服务工作,为估算“半程马拉松”的人数,对部分参赛选手作了调查:
调查人数 20 50 100 200 500 2000
参加人数 7 20 39 83 209 822
频率 0.350 0.400 0.390 0.415 0.418 0.411
请估算本次赛事参加“半程马拉松”人数的概率为 __________ .(精确到 0.01)
13. 如图,正方形ABCD的边长为6,分别以A,B为圆心,6为半径画弧BD,弧AC,则图中阴影部分的面积为__________________.
14. 在五个完全相同小球上分别写上1,2,3,4,5五个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从口袋中取出一个球记下数字后作为点P的纵坐标y.则在坐标平面内,点P(x,y)落在直线 y=﹣x+5上的概率是_____.
15. 在菱形中,,,的两边分别交边、于点E、F,且,记的外心为点P,则P、C两点间的最小距离为_____________.
16. 如图,在矩形ABCD中,,,点E从点A出发,沿射线AC以1cm/s的速度匀速移动.连接DE,过点E作,EF与射线BC相交于点F,作矩形DEFG,连接EG.设点E移动的时间为t(s),若EG与矩形ABCD的边平行,则t的值是______s.
三、解答题(本大题共11小题,共102分.解答时应写出文字说明、证明过程或演算步骤)
17. 计算:.
18. 先化简,再求值:,其中.
19. 已知关于x的一元二次方程有实数根.
(1)求k的取值范围.
(2)若方程有一个根为1,求方程的另一个根.
20. 如图,为边的中点,交的延长线于点,连接,平分,求证:四边形为菱形.
21. 如图,直线l1:y=kx+b与双曲线y=(x>0)交于A,B两点,与x轴交于点C,与y轴交于点E,已知点A(1,3),点C(4,0).
(1)求直线l1和双曲线的解析式;
(2)将△OCE沿直线l1翻折,点O落在第一象限内的点H处,求点H的坐标;
(3)如图,过点E作直线l2:y=3x+4交x轴负半轴于点F,在直线l2上是否存在点P,使得S△PBC=S△OBC?若存在,请直接写出所有符合条件的点P的坐标;如果不存在,请说明理由.
22. 如图,△ABC为⊙O的内接三角形,BC为⊙O的直径,在线段OC上取点D(不与端点重合),作DG⊥BC,分别交AC、圆周于E、F,连接AG,已知AG=EG.
(1)求证:AG为⊙O的切线;
(2)已知AG=2,填空:
①当四边形ABOF是菱形时,∠AEG= °;
②若OC=2DC,△AGE为等腰直角三角形,则AB= .
23. 一辆快车从甲地出发驶向乙地,在到达乙地后,立即按原路原速返回到甲地,快车出发一段时间后一辆慢车从甲地驶向乙地,中途因故停车后,继续按原速驶向乙地,两车距甲地路程与慢车行驶时间之间的函数图象如图所示,请结合图象解答下列问题:
(1)甲乙两地相距 ,快车行驶速度是 ,图中括号内的数值是 ;
(2)求快车从乙地返回甲地的过程中,y与x的函数解析式;
(3)慢车出发多长时间,两车相距.
24. 对于任意一个四位数m,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数m为“共生数”例如:,因为,所以3507是“共生数”:,因为,所以4135不是“共生数”;
(1)判断5313,6437是否为“共生数”?并说明理由;
(2)对于“共生数”n,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记.求满足各数位上的数字之和是偶数的所有n.
25. 【问题提出】如图1,用“圆规和无刻度的直尺”,作两条以为圆心的圆弧将已知扇形的面积三等分.
【问题联思】如图2,已知线段,请你用“圆规和无刻度的直尺”作一个以为底边,底角为的等腰三角形,并写出与的数量关系;
【问题再现】如图3,已知扇形,请你用“圆规和无刻度的直尺”作两条以点为圆心的圆弧,使扇形的面积被两条圆弧三等分.(友情提醒:保留作图痕迹,并用黑笔描线加深)
26. 在平面直角坐标系中,已知点A在y轴正半轴上.
(1)如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.
①________;
②如图1,已知菱形的顶点B、C、D在该二次函数的图象上,且轴,求菱形的边长;
③如图2,已知正方形的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究是否为定值.如果是,求出这个值;如果不是,请说明理由.
(2)已知正方形的顶点B、D在二次函数(a为常数,且)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.
27. (1)如图1,在矩形中,为边上一点,连接,若,过C作交于点F,
①求证:;
②若时,则 .
(2)如图2,在菱形中,,过作交的延长线于点,过作交于点,若时,求的值.
(3)如图3,在平行四边形中,,,,点E在上,且,点为上一点,连接,过作交平行四边形的边于点,若时,请直接写出的长.
同课章节目录
