27.1图形的相似 教学设计(表格的)数学人教版九年级下册
文档属性
| 名称 | 27.1图形的相似 教学设计(表格的)数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 164.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 15:06:56 | ||
图片预览

文档简介
教学设计
课程基本信息
课题 27.1图形的相似
教学目标
通过具体事例认识相似图形,了解相似图形、相似多边形和相似比的概念; 能根据多边形相似的定义进行相关的计算; 3.通过类比、操作、观察、猜想等数学活动,从边和角两个方面感受相似图形的特点,理解两个相似图形形状相同的含义,积累数学活动经验,感受从特殊到一般的研究问题方法,培养学生数学思维能力和推理论证能力.
教学内容
教学重点: 1. 认识相似图形,了解比例线段的定义; 2.掌握相似多边形的判定和相似多边形的性质。 教学难点: 运用相似多边形的性质进行相关的计算。
教学过程
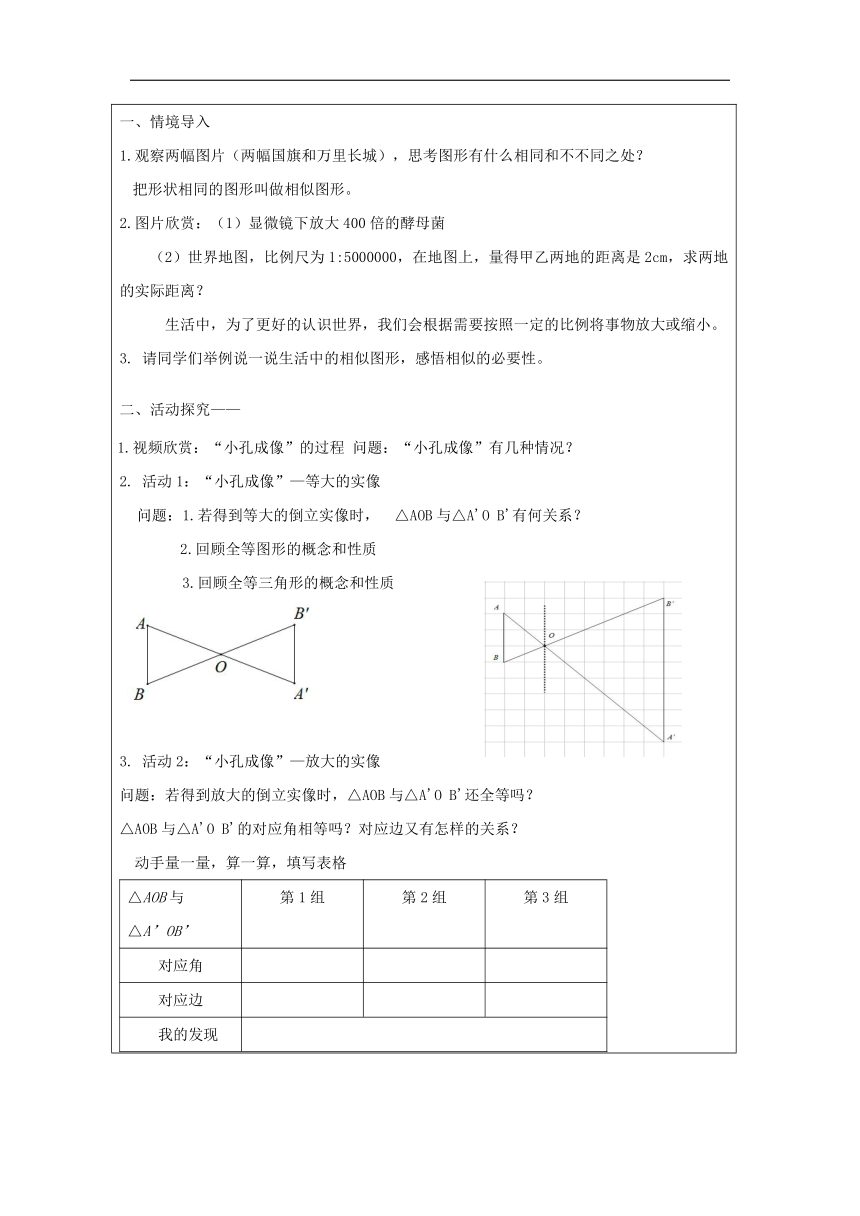
情境导入 1.观察两幅图片(两幅国旗和万里长城),思考图形有什么相同和不不同之处? 把形状相同的图形叫做相似图形。 2.图片欣赏:(1)显微镜下放大400倍的酵母菌 世界地图,比例尺为1:5000000,在地图上,量得甲乙两地的距离是2cm,求两地的实际距离? 生活中,为了更好的认识世界,我们会根据需要按照一定的比例将事物放大或缩小。 请同学们举例说一说生活中的相似图形,感悟相似的必要性。 活动探究—— 1 1.视频欣赏:“小孔成像”的过程 问题:“小孔成像”有几种情况? 活动1:“小孔成像”—等大的实像 问题:1.若得到等大的倒立实像时, △AOB与△A'O B'有何关系? 2.回顾全等图形的概念和性质 3.回顾全等三角形的概念和性质 活动2:“小孔成像”—放大的实像 问题:若得到放大的倒立实像时,△AOB与△A'O B'还全等吗? △AOB与△A'O B'的对应角相等吗?对应边又有怎样的关系? 动手量一量,算一算,填写表格 △AOB与 △A’OB’第1组第2组第3组对应角对应边我的发现
结论:两个三角形的对应角相等,对应边成比例 三、归纳小结 :1.相似多边形的定义:两个边数相同的多边形,如果它们的角分别相等、边成比例,那么这两个多边形叫做相似多边形. 相似多边形的特征:相似多边形的对应角相等,对应边成比例. 相似比:相似多边形对应边的比叫作相似比. 活动3:在方格纸中作出与原图形相似的图形并说出作图的理由 思考:任意的两个菱形(或矩形)是否相似?为什么? 四、例题讲解 例1 .如图,四边形 ABCD 和 EFGH 相似,求角α,β的大小和EH的长度 x. 解:∵ 四边形 ABCD 和 EFGH 相似, ∴ 它们的对应角相等.由此可得∠α=∠C=83°,∠A=∠E=118°. 在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°. ∵ 四边形ABCD和EFGH相似, ∴它们的对应边成比例,由此可得 解得 x = 28 例2.如图,已知△AEO相似于△ABC,△AOF相似于△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明理由. 解:四边形ABCD∽四边形AEOF ∵△AEO∽△ABC,∴∠1=∠2,∠3=∠4, ∵△AOF∽△ACD,∴∠5=∠6,∠7=∠8, ∴∠EOF=∠2+∠6=∠1+∠5=∠BCD, 又∵∠FAE=∠DAB,∴四边形AEOF∽四边形ABCD 小结思考 通过本节课的学习,你有哪些收获? 相似图形:形状相同的图形是相似图形 相似图形的形状相同,大小不一定相同,全等是特殊的相似 2.成比例线段(比例线段):对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段. 3.相似多边形:(1)定义:两个边数相同的多边形,各角分别相等,对应边成比例的多边形是相似多边形。 (2)性质:相似多边形的对应角相等,对应边成比例。 (3)相似比:相似多边形对应边的比。 结束语:给我最大快乐的, 不是已懂的知识,而是不断的学习; 不是已有的东西,而是不断的获取; 不是已达到的高度,而是继续不断的攀登! ——达尔文
课程基本信息
课题 27.1图形的相似
教学目标
通过具体事例认识相似图形,了解相似图形、相似多边形和相似比的概念; 能根据多边形相似的定义进行相关的计算; 3.通过类比、操作、观察、猜想等数学活动,从边和角两个方面感受相似图形的特点,理解两个相似图形形状相同的含义,积累数学活动经验,感受从特殊到一般的研究问题方法,培养学生数学思维能力和推理论证能力.
教学内容
教学重点: 1. 认识相似图形,了解比例线段的定义; 2.掌握相似多边形的判定和相似多边形的性质。 教学难点: 运用相似多边形的性质进行相关的计算。
教学过程
情境导入 1.观察两幅图片(两幅国旗和万里长城),思考图形有什么相同和不不同之处? 把形状相同的图形叫做相似图形。 2.图片欣赏:(1)显微镜下放大400倍的酵母菌 世界地图,比例尺为1:5000000,在地图上,量得甲乙两地的距离是2cm,求两地的实际距离? 生活中,为了更好的认识世界,我们会根据需要按照一定的比例将事物放大或缩小。 请同学们举例说一说生活中的相似图形,感悟相似的必要性。 活动探究—— 1 1.视频欣赏:“小孔成像”的过程 问题:“小孔成像”有几种情况? 活动1:“小孔成像”—等大的实像 问题:1.若得到等大的倒立实像时, △AOB与△A'O B'有何关系? 2.回顾全等图形的概念和性质 3.回顾全等三角形的概念和性质 活动2:“小孔成像”—放大的实像 问题:若得到放大的倒立实像时,△AOB与△A'O B'还全等吗? △AOB与△A'O B'的对应角相等吗?对应边又有怎样的关系? 动手量一量,算一算,填写表格 △AOB与 △A’OB’第1组第2组第3组对应角对应边我的发现
结论:两个三角形的对应角相等,对应边成比例 三、归纳小结 :1.相似多边形的定义:两个边数相同的多边形,如果它们的角分别相等、边成比例,那么这两个多边形叫做相似多边形. 相似多边形的特征:相似多边形的对应角相等,对应边成比例. 相似比:相似多边形对应边的比叫作相似比. 活动3:在方格纸中作出与原图形相似的图形并说出作图的理由 思考:任意的两个菱形(或矩形)是否相似?为什么? 四、例题讲解 例1 .如图,四边形 ABCD 和 EFGH 相似,求角α,β的大小和EH的长度 x. 解:∵ 四边形 ABCD 和 EFGH 相似, ∴ 它们的对应角相等.由此可得∠α=∠C=83°,∠A=∠E=118°. 在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°. ∵ 四边形ABCD和EFGH相似, ∴它们的对应边成比例,由此可得 解得 x = 28 例2.如图,已知△AEO相似于△ABC,△AOF相似于△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明理由. 解:四边形ABCD∽四边形AEOF ∵△AEO∽△ABC,∴∠1=∠2,∠3=∠4, ∵△AOF∽△ACD,∴∠5=∠6,∠7=∠8, ∴∠EOF=∠2+∠6=∠1+∠5=∠BCD, 又∵∠FAE=∠DAB,∴四边形AEOF∽四边形ABCD 小结思考 通过本节课的学习,你有哪些收获? 相似图形:形状相同的图形是相似图形 相似图形的形状相同,大小不一定相同,全等是特殊的相似 2.成比例线段(比例线段):对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段. 3.相似多边形:(1)定义:两个边数相同的多边形,各角分别相等,对应边成比例的多边形是相似多边形。 (2)性质:相似多边形的对应角相等,对应边成比例。 (3)相似比:相似多边形对应边的比。 结束语:给我最大快乐的, 不是已懂的知识,而是不断的学习; 不是已有的东西,而是不断的获取; 不是已达到的高度,而是继续不断的攀登! ——达尔文
