数学人教A版（2019）必修第二册8.3.2旋转体的表面积与体积 课件（共24张ppt）

(共24张PPT)
8.3.2圆柱、圆锥、圆台的表面积和体积
第八章立体几何初步
回顾所学的有关公式
圆面积公式：
圆周长公式：
扇形面积公式：
扇形弧长公式：
r
思考 思考
一、圆柱,圆锥,圆台的的表面积
与多面体的表面积一样，圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和.
探究新知
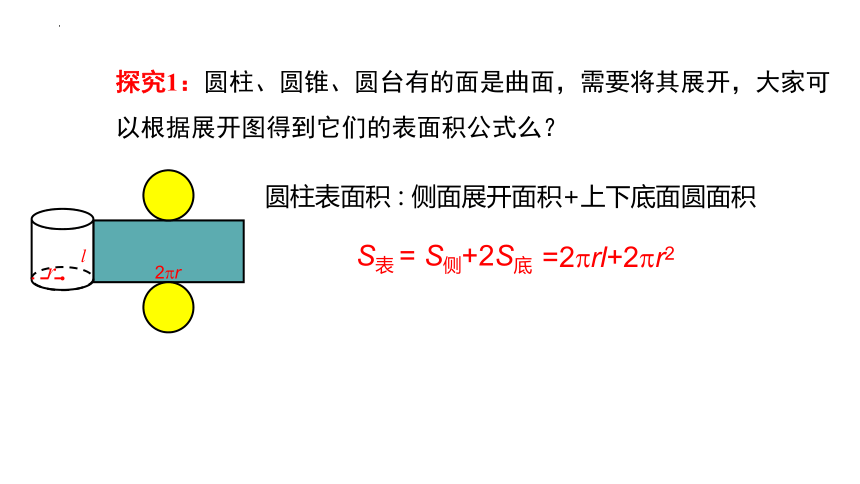
探究1：圆柱、圆锥、圆台有的面是曲面，需要将其展开，大家可以根据展开图得到它们的表面积公式么？
圆柱表面积 : 侧面展开面积+上下底面圆面积
S表 = S侧+2S底
2 r
=2 rl+2 r2
探究新知
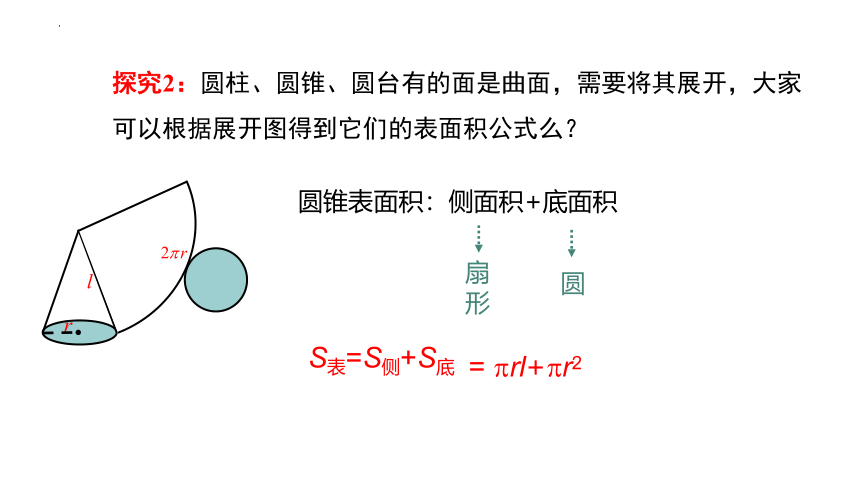
探究2：圆柱、圆锥、圆台有的面是曲面，需要将其展开，大家可以根据展开图得到它们的表面积公式么？
扇形
圆
S表=S侧+S底
= rl+ r2
圆锥表面积：侧面积+底面积
探究新知
探究：圆柱、圆锥、圆台有的面是曲面，需要将其展开，大家可以根据展开图得到它们的表面积公式么？
设小扇形的母线长l′，圆台上底面半径为r1，下底面半径为r2 ，扇环的母线长为l，
由相似三角形得：
2 r1
2 r2
探究新知
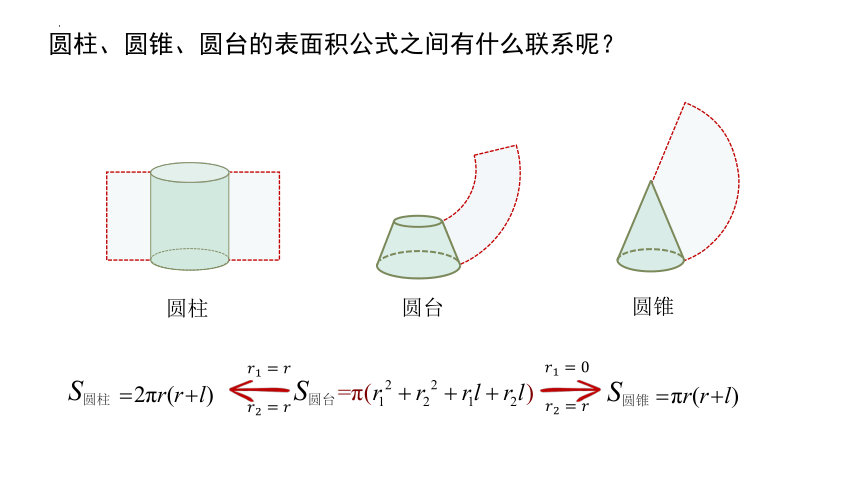
圆柱、圆锥、圆台的表面积公式之间有什么联系呢？
圆柱
圆锥
圆台
S圆台
S圆柱
S圆锥
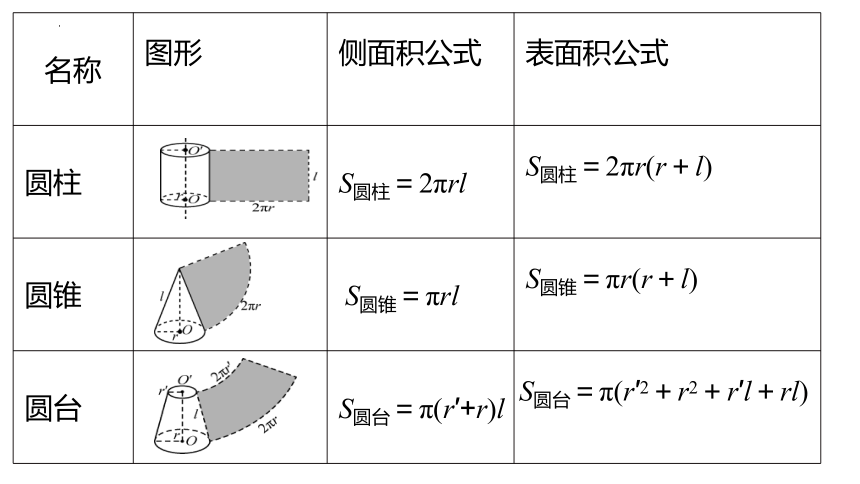
名称 图形 侧面积公式 表面积公式
圆柱 S圆柱＝2πrl S圆柱＝2πr(r＋l)
圆锥 S圆锥＝πrl S圆锥＝πr(r＋l)
圆台 S圆台＝π(r′+r)l S圆台＝π(r′2＋r2＋r′l＋rl)
探究新知
(1)将一个边长分别为4π，8π的矩形卷成一个圆柱的侧面，则这个圆柱(包含上、下底面)的表面积是(　　)
A．40π2　　　　　　　　 B．64π2
C．32π2或64π2 D．32π2＋8π或32π2＋32π
D
例1
(2)若一个圆锥的轴截面是边长为4 cm 的等边三角形，则这个圆锥的侧面积为________cm2，表面积为________cm2.
【解析】 如图，因为圆锥的轴截面是边长为4 cm的等边三角形，所以OB＝2 cm，PB＝4 cm，所以圆锥的侧面积S侧＝π×2×4＝8π(cm2)，表面积S表＝8π＋π×22＝12π(cm2)．
12π
8π
(3)圆台的上、下底面半径和高的比为1∶4∶4，若母线长为10，则圆台的表面积为(　　)
A. 81π　 B. 100π C. 168π D. 169π
C
1.民间娱乐健身工具陀螺起源于我国，最早出土的石制陀螺是在山西夏县发现的新石器时代遗址．如图所示的是一个陀螺的立体结构图．已知底面圆的直径，圆柱体的高，圆锥体的高，则这个陀螺的表面积是（ ）
A． B． C． D．
【解析】圆柱、圆锥的底面半径为，
圆锥的母线长为，
所以陀螺的表面积是．
练习
B
2.若一个圆锥的轴截面是一个腰长为，底边上的高为1的等腰三角形，则该圆锥的侧面积为（ ）
A． B． C． D．
【解析】由题意可得该圆锥的轴截面是一个等腰直角三角形，腰长为，底边长为2，
所以圆锥的母线长，底面圆半径，
所以该圆锥的侧面积为．
B
3.《九章算术》中将圆台称为“圆亭”．已知某圆亭的高为3，上底面半径为1，下底面半径为5，则此圆亭的表面积为（ ）
A． B． C． D．
【解析】由题意，可作该圆亭的轴截面，如图所示：
则圆亭的高，上底面半径，下底面半径，
母线5，
所以圆台的表面积．
D
4.已知圆台的上底面半径为1，下底面半径为2，母线与下底面所成的角为，则该圆台的表面积为（ ）
A． B． C． D．
【解析】由题意，得上底面面积为，下底面面积为，
由图形可得，，
母线与下底面所成的角为，故，
故圆台的母线长为2，所以侧面积为，
所以该圆台的表面积为．
C
圆柱的体积：
圆锥的体积：
V棱柱=Sh.
棱柱的体积:
棱锥的体积：
棱台的体积:
圆台的体积:

二、圆柱,圆锥,圆台的的表面积

例2
（2）某圆锥的轴截面是等腰直角三角形，侧面积是 ，
则圆锥的体积是( ).
A. B. C. D.
A
[解析] （1）当圆柱的高为 时， ;
当圆柱的高为 时， .
（2）作圆锥的轴截面，如图所示：
由题意知，在 中， ， .
设圆锥的高为 ，底面半径为 ，则 ， .
由 ，即 ，解得 ，则 .
故圆锥的体积 .
【变式4-2】（2024·高一·山东济宁·期末）已知圆锥的高为，侧面积是底面积的2倍，则该圆锥的体积是 ．
【答案】
【解析】设圆锥的底面半径为，则母线长为，侧面积为，
底面积为，由题意可得，解得，
则该圆锥的体积是．
故答案为：．
题型四：圆柱、圆锥、圆台的体积
1.已知圆台的上、下底面半径和高的比为 ，母线长为10，
则圆台的体积为______.

[解析] 设上底面半径为 ，则下底面半径 ，高 ，如图.
由题意得， ，解得 .
，
.
练习
3.已知圆锥PO的底面半径为，O为底面圆心，PA，PB为圆锥的母线，，若的面积等于，则该圆锥的体积为（ ）
A． B． C． D．
B
圆锥