18.2.3 正方形 同步练习(含答案)
文档属性
| 名称 | 18.2.3 正方形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 10:55:05 | ||
图片预览


文档简介
18.1 平行四边形
18.2.3 正方形
一、选择题
1.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( )
A.9 B.12 C.15 D.20
第1题图 第2题图 第3题图
2.如图,四边形ABCD是正方形,AD平行于x轴,A,C两点的坐标分别为(-2,2),(1,-1),则点B的坐标是( )
A.(-1,-2) B.(-1,-3) C.(-2,-1) D.(-3,-1)
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( )
A.10° B.15° C.20° D.30°
4.下列条件中,能使菱形ABCD为正方形的是( )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
5.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
6.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等 c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( )
A.仅① B.仅③ C.①② D.②③
第6题图 第7题图 第8题图
7.【2023河北】如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC=( )
A.4 B.8 C.12 D.16
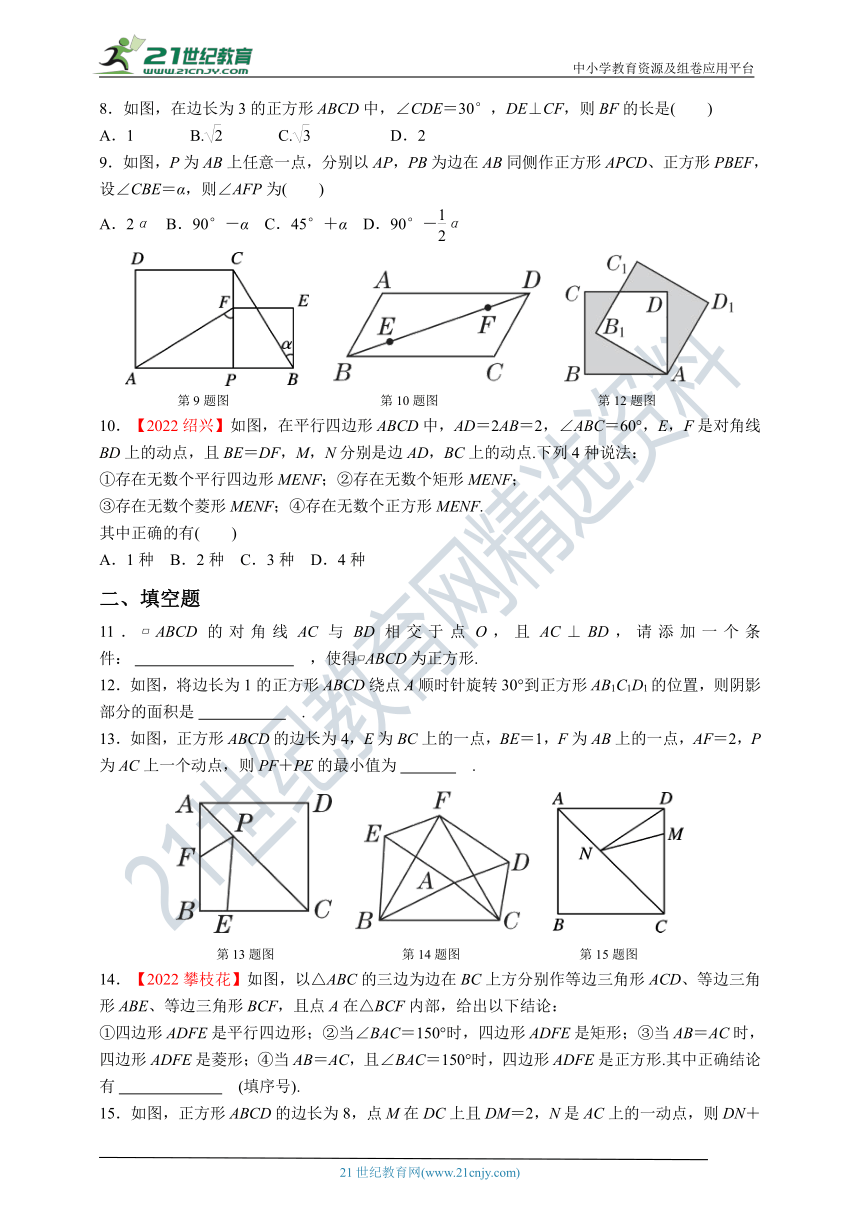
8.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )
A.1 B. C. D.2
9.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°-α C.45°+α D.90°-α
第9题图 第10题图 第12题图
10.【2022绍兴】如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,BC上的动点.下列4种说法:
①存在无数个平行四边形MENF;②存在无数个矩形MENF;
③存在无数个菱形MENF;④存在无数个正方形MENF.
其中正确的有( )
A.1种 B.2种 C.3种 D.4种
二、填空题
11. ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得 ABCD为正方形.
12.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到正方形AB1C1D1的位置,则阴影部分的面积是 .
13.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .
第13题图 第14题图 第15题图
14.【2022攀枝花】如图,以△ABC的三边为边在BC上方分别作等边三角形ACD、等边三角形ABE、等边三角形BCF,且点A在△BCF内部,给出以下结论:
①四边形ADFE是平行四边形;②当∠BAC=150°时,四边形ADFE是矩形;③当AB=AC时,四边形ADFE是菱形;④当AB=AC,且∠BAC=150°时,四边形ADFE是正方形.其中正确结论有 (填序号).
15.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
三、解答题
16.【2022随州】如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积为20,AB=5,求CF的长.
17.【2023十堰】如图, ABCD的对角线AC,BD交于点O,分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,连接BP,CP.
(1)试判断四边形BPCO的形状,并说明理由;
(2)请说明当 ABCD的对角线满足什么条件时,四边形BPCO是正方形?
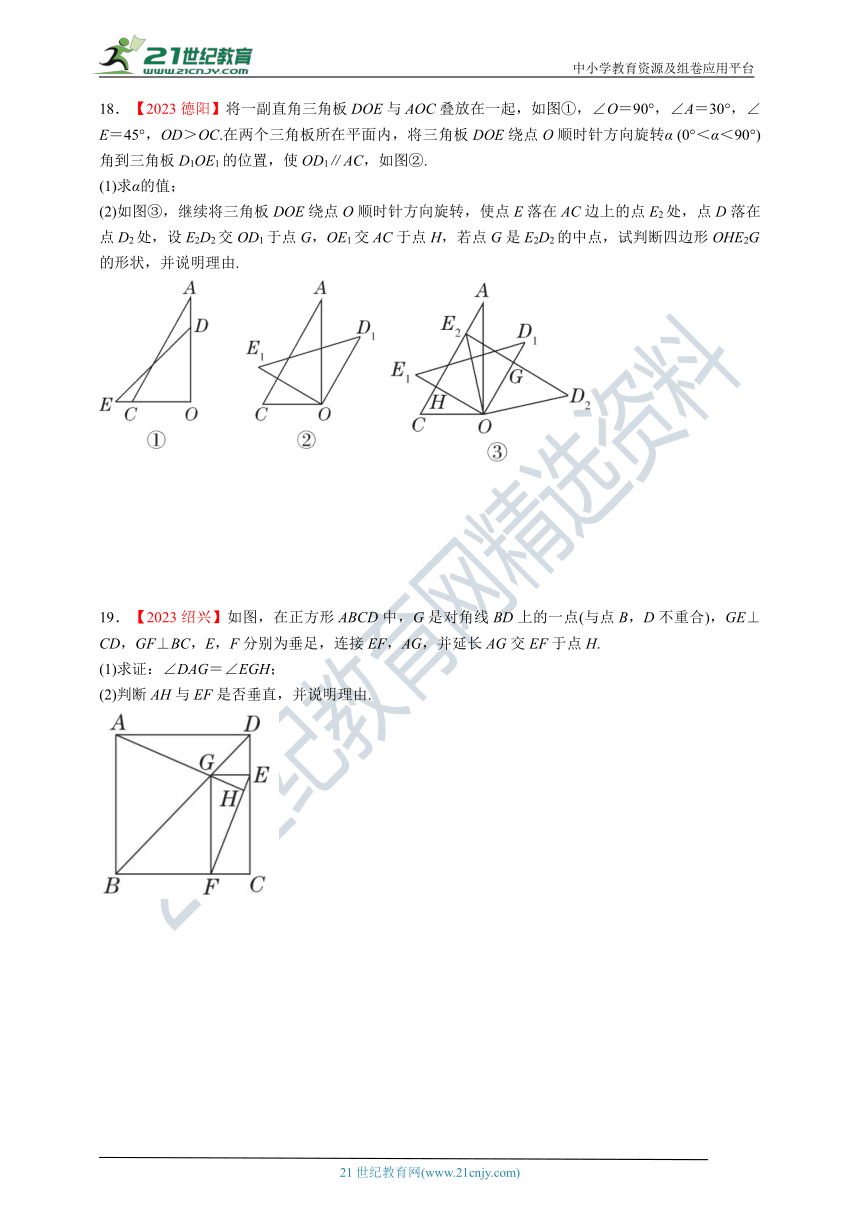
18.【2023德阳】将一副直角三角板DOE与AOC叠放在一起,如图①,∠O=90°,∠A=30°,∠E=45°,OD>OC.在两个三角板所在平面内,将三角板DOE绕点O顺时针方向旋转α (0°<α<90°)角到三角板D1OE1的位置,使OD1∥AC,如图②.
(1)求α的值;
(2)如图③,继续将三角板DOE绕点O顺时针方向旋转,使点E落在AC边上的点E2处,点D落在点D2处,设E2D2交OD1于点G,OE1交AC于点H,若点G是E2D2的中点,试判断四边形OHE2G的形状,并说明理由.
19.【2023绍兴】如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,E,F分别为垂足,连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
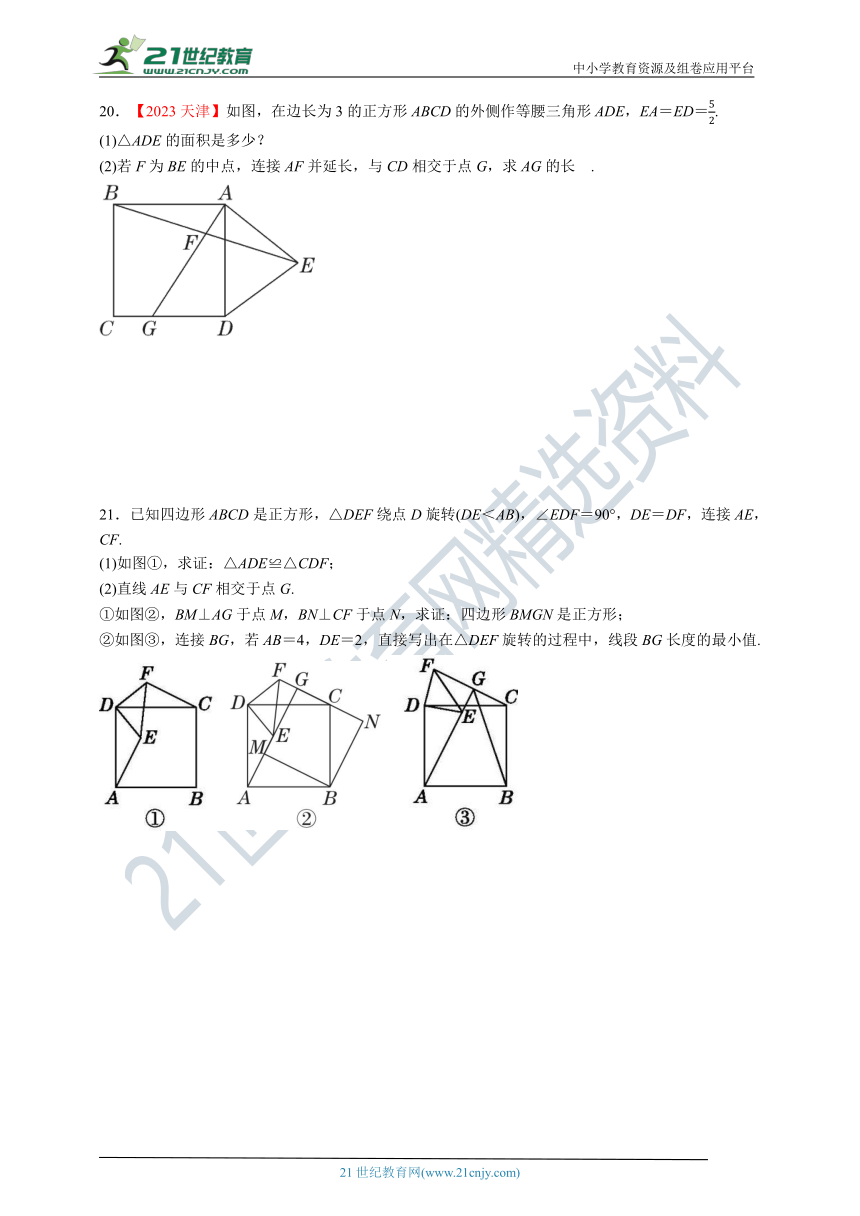
20.【2023天津】如图,在边长为3的正方形ABCD的外侧作等腰三角形ADE,EA=ED=.
(1)△ADE的面积是多少?
(2)若F为BE的中点,连接AF并延长,与CD相交于点G,求AG的长 .
21.已知四边形ABCD是正方形,△DEF绕点D旋转(DE<AB),∠EDF=90°,DE=DF,连接AE,CF.
(1)如图①,求证:△ADE≌△CDF;
(2)直线AE与CF相交于点G.
①如图②,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图③,连接BG,若AB=4,DE=2,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
22.如图①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C,D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)猜想图①中线段BG、线段DE的数量关系及所在直线的位置关系,并说明理由;
(2)将图①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图②③的情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图②证明你的判断.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( A )
A.9 B.12 C.15 D.20
第1题图 第2题图 第3题图
2.如图,四边形ABCD是正方形,AD平行于x轴,A,C两点的坐标分别为(-2,2),(1,-1),则点B的坐标是( C )
A.(-1,-2) B.(-1,-3) C.(-2,-1) D.(-3,-1)
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( C )
A.10° B.15° C.20° D.30°
4.下列条件中,能使菱形ABCD为正方形的是( B )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
5.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( C )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
6.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等 c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( C )
A.仅① B.仅③ C.①② D.②③
第6题图 第7题图 第8题图
7.【2023河北】如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC=( B )
A.4 B.8 C.12 D.16
8.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( C )
A.1 B. C. D.2
9.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( B )
A.2α B.90°-α C.45°+α D.90°-α
第9题图 第10题图 第12题图
10.【2022绍兴】如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,BC上的动点.下列4种说法:
①存在无数个平行四边形MENF;②存在无数个矩形MENF;
③存在无数个菱形MENF;④存在无数个正方形MENF.
其中正确的有( C )
A.1种 B.2种 C.3种 D.4种
【解析】连接AC,MN,AC交BD于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵BE=DF,∴OE=OF.当MN过点O时,易证OM=ON,∴四边形MENF为平行四边形.∵点E,F,M,N是动点,∴存在无数个平行四边形MENF;当MN过点O,MN=EF时,四边形MENF是矩形.∵点E,F,M,N是动点,∴存在无数个矩形MENF;当MN过点O,MN⊥EF时,四边形MENF是菱形. ∵点E,F是动点,∴存在无数个菱形MENF;当MN过点O,MN=EF且MN⊥EF时,四边形MENF是正方形,符合要求的正方形只有一个,故①②③正确,④错误.
二、填空题
11. ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得 ABCD为正方形.
【答案】AC=BD(答案不唯一)
【解析】根据题意可知 ABCD为菱形,要使菱形ABCD为正方形,添加的条件为AB⊥AD,AC=BD等.
12.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到正方形AB1C1D1的位置,则阴影部分的面积是 .
【答案】2-
13.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .
【答案】
【解析】过点E作EH⊥AD于H,在AD上取一点M,使得AM=2,易知点F,M关于AC所在直线对称.连接EM,交AC于点P',连接P'F,则P'F=P'M.易得P'M+P'E的值为PF+PE的最小值,即EM的长为PF+PE的最小值.易得EM==.
第13题图 第14题图 第15题图
14.【2022攀枝花】如图,以△ABC的三边为边在BC上方分别作等边三角形ACD、等边三角形ABE、等边三角形BCF,且点A在△BCF内部,给出以下结论:
①四边形ADFE是平行四边形;②当∠BAC=150°时,四边形ADFE是矩形;③当AB=AC时,四边形ADFE是菱形;④当AB=AC,且∠BAC=150°时,四边形ADFE是正方形.其中正确结论有 (填序号).
【答案】①②③④
【解析】①利用“SAS”证明△EFB≌△ACB,得出EF=AC=AD;同理可得△CDF≌△CAB,得DF=AB=AE;根据两组对边分别相等的四边形是平行四边形得出四边形ADFE是平行四边形,结论①正确;②当∠BAC=150°时,求出∠EAD=90°,根据有一个角是90°的平行四边形是矩形即可判断结论②正确;③先证明AE=AD,再根据有一组邻边相等的平行四边形是菱形即可判断结论③正确;④根据正方形的判定:既是菱形,又是矩形的四边形是正方形即可判断结论④正确.
15.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
【答案】10
【解析】连接BM交AC于点P,∵点N为AC上的动点,由三角形两边之和大于第三边,且正方形是轴对称图形知,当点N运动到点P时,DN+MN=BP+PM=BM,DN+MN的最小值为BM的长度,∵四边形ABCD为正方形,∴BC=CD=8,CM=8-2=6,∠BCM=90°,∴BM==10,∴DN+MN的最小值是10.
三、解答题
16.【2022随州】如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积为20,AB=5,求CF的长.
(1)【证明】∵四边形BEDF为正方形,
∴EB=DF.
∵四边形ABCD是平行四边形,
∴AB=DC.∴AE=CF.
(2)【解】∵四边形BEDF为正方形,
∴DE=EB,DE⊥AB.
∵平行四边形ABCD的面积为20,AB=5,
∴DE=EB=4.∴AE=AB-EB=5-4=1.
由(1)知AE=CF,∴CF=1.
17.【2023十堰】如图, ABCD的对角线AC,BD交于点O,分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,连接BP,CP.
(1)试判断四边形BPCO的形状,并说明理由;
(2)请说明当 ABCD的对角线满足什么条件时,四边形BPCO是正方形?
【解】(1)四边形BPCO为平行四边形.
理由:∵四边形ABCD为平行四边形,∴OC=OA=AC,OB=OD=BD.∵分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P.∴OB=CP,BP=OC,∴四边形BPCO为平行四边形.
【解】(2)当AC⊥BD,AC=BD时,四边形BPCO为正方形.
∵AC⊥BD,∴∠BOC=90°.
∵AC=BD,OB=BD,OC=AC,
∴OB=OC.
又∵四边形BPCO为平行四边形,∴四边形BPCO为正方形.
18.【2023德阳】将一副直角三角板DOE与AOC叠放在一起,如图①,∠O=90°,∠A=30°,∠E=45°,OD>OC.在两个三角板所在平面内,将三角板DOE绕点O顺时针方向旋转α (0°<α<90°)角到三角板D1OE1的位置,使OD1∥AC,如图②.
(1)求α的值;
(2)如图③,继续将三角板DOE绕点O顺时针方向旋转,使点E落在AC边上的点E2处,点D落在点D2处,设E2D2交OD1于点G,OE1交AC于点H,若点G是E2D2的中点,试判断四边形OHE2G的形状,并说明理由.
(1)【解】∵OD1∥AC,∴∠A=∠AOD1=30°.
∵将三角板DOE绕点O顺时针方向旋转α(0°<α<90°)角到三角板D1OE1的位置,∴∠AOD1=α=30°.
【解】(2)四边形OHE2G是正方形,理由如下:
∵∠E2OD2=90°,OD2=OE2,点G是E2D2的中点,
∴E2G=OG,E2G⊥OG.∵OD1∥AC,∠GOH=90°,
∴∠AHO=180°-90°=90°,∴四边形OHE2G是矩形.
又∵E2G=OG,∴四边形OHE2G是正方形.
19.【2023绍兴】如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,E,F分别为垂足,连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
(1)【证明】在正方形ABCD中,AD⊥CD,GE⊥CD,∴∠ADE=∠GEC=90°,
∴AD∥GE,∴∠DAG=∠EGH.
(2)【解】AH⊥EF,理由如下:
连接GC交EF于点O,如图.
在正方形ABCD中,AD=CD,
∵BD为正方形ABCD的对角线,
∴∠ADG=∠CDG=45°.
又∵DG=DG,∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG.
在正方形ABCD中,∠ECF=90°.
又∵GE⊥CD,GF⊥BC,
∴四边形FCEG为矩形,
∴OE=EF,OC=CG,EF=CG,∴OE=OC,
∴∠OEC=∠OCE,∴∠DAG=∠OEC.
由(1)得∠DAG=∠EGH,
∴∠EGH=∠OEC,
∴∠EGH+∠GEH=∠OEC+∠GEH=∠GEC=90°,
∴∠GHE=90°,∴AH⊥EF.
20.【2023天津】如图,在边长为3的正方形ABCD的外侧作等腰三角形ADE,EA=ED=.
(1)△ADE的面积是多少?
(2)若F为BE的中点,连接AF并延长,与CD相交于点G,求AG的长 .
(1)如图,过点E作EM⊥AD于点M.
∵EA=ED=,AD=3,
∴AM=DM=AD=,
∴EM==2,
∴△ADE的面积为AD·EM=×3×2=3.
(2)如图,延长EM交AG于点N,交BC于点P.
∵四边形ABCD是正方形,
∴∠ADC=∠ABC=90°,BC∥AD,AB∥CD,
∴EP⊥BC.
又∵EP⊥AD,
∴四边形ABPM是矩形,
∴PM=AB=3,AB∥EP,
∴EP=5,∠ABF=∠NEF,EP∥CD.
∵F为BE的中点,∴BF=EF,
又∵∠AFB=∠NFE,∴△ABF≌△NEF(ASA),
∴EN=AB=3,∴MN=1.
由PM∥CD,AM=DM,易知AN=NG,
∴MN为△AGD的中位线,
∴GD=2MN=2,
∴AG==.
21.已知四边形ABCD是正方形,△DEF绕点D旋转(DE<AB),∠EDF=90°,DE=DF,连接AE,CF.
(1)如图①,求证:△ADE≌△CDF;
(2)直线AE与CF相交于点G.
①如图②,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图③,连接BG,若AB=4,DE=2,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
(1)【证明】∵四边形ABCD是正方形,∴AD=DC,∠ADC=90°.∵∠EDF=90°,∴∠ADC=∠EDF.
∴∠ADE=∠CDF.
∴△ADE≌△CDF(SAS).
(2)①【证明】如图②,设AG与CD相交于点P.
∵∠ADP=90°,∴∠DAP+∠DPA=90°.
∵△ADE≌△CDF,∴∠DAE=∠DCF.
又∵∠DPA=∠GPC,
∴∠DAE+∠DPA=∠GPC+∠GCP=90°.
∴∠PGN=90°.
又∵BM⊥AG,BN⊥GN,
∴四边形BMGN是矩形.
∴∠MBN=90°.∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°=∠MBN.∴∠ABM=∠CBN.
又∵∠AMB=∠BNC=90°,∴△AMB≌△CNB.
∴MB=NB.
∴矩形BMGN是正方形.
②【解】线段BG长度的最小值为2.
22.如图①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C,D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)猜想图①中线段BG、线段DE的数量关系及所在直线的位置关系,并说明理由;
(2)将图①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图②③的情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图②证明你的判断.
(1)【解】BG=DE,BG⊥DE.理由如下:
如图①,延长BG交DE于点H.
∵四边形ABCD和四边形CEFG都是正方形,
∴BC=DC,∠BCG=∠DCE=90°,CG=CE.
∴△BCG≌△DCE.∴BG=DE,∠1=∠2.
∵∠1+∠CGB=90°,∠CGB=∠DGH,∴∠2+∠DGH=90°.∴∠DHG=90°.∴BH⊥DE,即BG⊥DE.
(2)【解】BG=DE,BG⊥DE仍然成立.
证明:如图②,设BG与DE相交于点O,DC与BG相交于点H.∵四边形ABCD、四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG=90°.
∴∠BCG=∠DCE. ∴△BCG≌△DCE.
∴BG=DE,∠CBG=∠CDE.
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°.∴∠DOH=90°.∴BG⊥DE.
18.2.3 正方形
一、选择题
1.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( )
A.9 B.12 C.15 D.20
第1题图 第2题图 第3题图
2.如图,四边形ABCD是正方形,AD平行于x轴,A,C两点的坐标分别为(-2,2),(1,-1),则点B的坐标是( )
A.(-1,-2) B.(-1,-3) C.(-2,-1) D.(-3,-1)
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( )
A.10° B.15° C.20° D.30°
4.下列条件中,能使菱形ABCD为正方形的是( )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
5.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
6.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等 c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( )
A.仅① B.仅③ C.①② D.②③
第6题图 第7题图 第8题图
7.【2023河北】如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC=( )
A.4 B.8 C.12 D.16
8.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )
A.1 B. C. D.2
9.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°-α C.45°+α D.90°-α
第9题图 第10题图 第12题图
10.【2022绍兴】如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,BC上的动点.下列4种说法:
①存在无数个平行四边形MENF;②存在无数个矩形MENF;
③存在无数个菱形MENF;④存在无数个正方形MENF.
其中正确的有( )
A.1种 B.2种 C.3种 D.4种
二、填空题
11. ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得 ABCD为正方形.
12.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到正方形AB1C1D1的位置,则阴影部分的面积是 .
13.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .
第13题图 第14题图 第15题图
14.【2022攀枝花】如图,以△ABC的三边为边在BC上方分别作等边三角形ACD、等边三角形ABE、等边三角形BCF,且点A在△BCF内部,给出以下结论:
①四边形ADFE是平行四边形;②当∠BAC=150°时,四边形ADFE是矩形;③当AB=AC时,四边形ADFE是菱形;④当AB=AC,且∠BAC=150°时,四边形ADFE是正方形.其中正确结论有 (填序号).
15.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
三、解答题
16.【2022随州】如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积为20,AB=5,求CF的长.
17.【2023十堰】如图, ABCD的对角线AC,BD交于点O,分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,连接BP,CP.
(1)试判断四边形BPCO的形状,并说明理由;
(2)请说明当 ABCD的对角线满足什么条件时,四边形BPCO是正方形?
18.【2023德阳】将一副直角三角板DOE与AOC叠放在一起,如图①,∠O=90°,∠A=30°,∠E=45°,OD>OC.在两个三角板所在平面内,将三角板DOE绕点O顺时针方向旋转α (0°<α<90°)角到三角板D1OE1的位置,使OD1∥AC,如图②.
(1)求α的值;
(2)如图③,继续将三角板DOE绕点O顺时针方向旋转,使点E落在AC边上的点E2处,点D落在点D2处,设E2D2交OD1于点G,OE1交AC于点H,若点G是E2D2的中点,试判断四边形OHE2G的形状,并说明理由.
19.【2023绍兴】如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,E,F分别为垂足,连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
20.【2023天津】如图,在边长为3的正方形ABCD的外侧作等腰三角形ADE,EA=ED=.
(1)△ADE的面积是多少?
(2)若F为BE的中点,连接AF并延长,与CD相交于点G,求AG的长 .
21.已知四边形ABCD是正方形,△DEF绕点D旋转(DE<AB),∠EDF=90°,DE=DF,连接AE,CF.
(1)如图①,求证:△ADE≌△CDF;
(2)直线AE与CF相交于点G.
①如图②,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图③,连接BG,若AB=4,DE=2,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
22.如图①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C,D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)猜想图①中线段BG、线段DE的数量关系及所在直线的位置关系,并说明理由;
(2)将图①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图②③的情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图②证明你的判断.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,菱形ABCD中,∠B=60°,AB=3,则以AC为边长的正方形ACEF的面积为( A )
A.9 B.12 C.15 D.20
第1题图 第2题图 第3题图
2.如图,四边形ABCD是正方形,AD平行于x轴,A,C两点的坐标分别为(-2,2),(1,-1),则点B的坐标是( C )
A.(-1,-2) B.(-1,-3) C.(-2,-1) D.(-3,-1)
3.如图,在正方形ABCD中,E为对角线BD上一点,连接AE,CE,∠BCE=70°,则∠EAD为( C )
A.10° B.15° C.20° D.30°
4.下列条件中,能使菱形ABCD为正方形的是( B )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
5.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( C )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
6.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等 c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( C )
A.仅① B.仅③ C.①② D.②③
第6题图 第7题图 第8题图
7.【2023河北】如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC=( B )
A.4 B.8 C.12 D.16
8.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( C )
A.1 B. C. D.2
9.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( B )
A.2α B.90°-α C.45°+α D.90°-α
第9题图 第10题图 第12题图
10.【2022绍兴】如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,BC上的动点.下列4种说法:
①存在无数个平行四边形MENF;②存在无数个矩形MENF;
③存在无数个菱形MENF;④存在无数个正方形MENF.
其中正确的有( C )
A.1种 B.2种 C.3种 D.4种
【解析】连接AC,MN,AC交BD于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵BE=DF,∴OE=OF.当MN过点O时,易证OM=ON,∴四边形MENF为平行四边形.∵点E,F,M,N是动点,∴存在无数个平行四边形MENF;当MN过点O,MN=EF时,四边形MENF是矩形.∵点E,F,M,N是动点,∴存在无数个矩形MENF;当MN过点O,MN⊥EF时,四边形MENF是菱形. ∵点E,F是动点,∴存在无数个菱形MENF;当MN过点O,MN=EF且MN⊥EF时,四边形MENF是正方形,符合要求的正方形只有一个,故①②③正确,④错误.
二、填空题
11. ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得 ABCD为正方形.
【答案】AC=BD(答案不唯一)
【解析】根据题意可知 ABCD为菱形,要使菱形ABCD为正方形,添加的条件为AB⊥AD,AC=BD等.
12.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到正方形AB1C1D1的位置,则阴影部分的面积是 .
【答案】2-
13.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .
【答案】
【解析】过点E作EH⊥AD于H,在AD上取一点M,使得AM=2,易知点F,M关于AC所在直线对称.连接EM,交AC于点P',连接P'F,则P'F=P'M.易得P'M+P'E的值为PF+PE的最小值,即EM的长为PF+PE的最小值.易得EM==.
第13题图 第14题图 第15题图
14.【2022攀枝花】如图,以△ABC的三边为边在BC上方分别作等边三角形ACD、等边三角形ABE、等边三角形BCF,且点A在△BCF内部,给出以下结论:
①四边形ADFE是平行四边形;②当∠BAC=150°时,四边形ADFE是矩形;③当AB=AC时,四边形ADFE是菱形;④当AB=AC,且∠BAC=150°时,四边形ADFE是正方形.其中正确结论有 (填序号).
【答案】①②③④
【解析】①利用“SAS”证明△EFB≌△ACB,得出EF=AC=AD;同理可得△CDF≌△CAB,得DF=AB=AE;根据两组对边分别相等的四边形是平行四边形得出四边形ADFE是平行四边形,结论①正确;②当∠BAC=150°时,求出∠EAD=90°,根据有一个角是90°的平行四边形是矩形即可判断结论②正确;③先证明AE=AD,再根据有一组邻边相等的平行四边形是菱形即可判断结论③正确;④根据正方形的判定:既是菱形,又是矩形的四边形是正方形即可判断结论④正确.
15.如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
【答案】10
【解析】连接BM交AC于点P,∵点N为AC上的动点,由三角形两边之和大于第三边,且正方形是轴对称图形知,当点N运动到点P时,DN+MN=BP+PM=BM,DN+MN的最小值为BM的长度,∵四边形ABCD为正方形,∴BC=CD=8,CM=8-2=6,∠BCM=90°,∴BM==10,∴DN+MN的最小值是10.
三、解答题
16.【2022随州】如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积为20,AB=5,求CF的长.
(1)【证明】∵四边形BEDF为正方形,
∴EB=DF.
∵四边形ABCD是平行四边形,
∴AB=DC.∴AE=CF.
(2)【解】∵四边形BEDF为正方形,
∴DE=EB,DE⊥AB.
∵平行四边形ABCD的面积为20,AB=5,
∴DE=EB=4.∴AE=AB-EB=5-4=1.
由(1)知AE=CF,∴CF=1.
17.【2023十堰】如图, ABCD的对角线AC,BD交于点O,分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,连接BP,CP.
(1)试判断四边形BPCO的形状,并说明理由;
(2)请说明当 ABCD的对角线满足什么条件时,四边形BPCO是正方形?
【解】(1)四边形BPCO为平行四边形.
理由:∵四边形ABCD为平行四边形,∴OC=OA=AC,OB=OD=BD.∵分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P.∴OB=CP,BP=OC,∴四边形BPCO为平行四边形.
【解】(2)当AC⊥BD,AC=BD时,四边形BPCO为正方形.
∵AC⊥BD,∴∠BOC=90°.
∵AC=BD,OB=BD,OC=AC,
∴OB=OC.
又∵四边形BPCO为平行四边形,∴四边形BPCO为正方形.
18.【2023德阳】将一副直角三角板DOE与AOC叠放在一起,如图①,∠O=90°,∠A=30°,∠E=45°,OD>OC.在两个三角板所在平面内,将三角板DOE绕点O顺时针方向旋转α (0°<α<90°)角到三角板D1OE1的位置,使OD1∥AC,如图②.
(1)求α的值;
(2)如图③,继续将三角板DOE绕点O顺时针方向旋转,使点E落在AC边上的点E2处,点D落在点D2处,设E2D2交OD1于点G,OE1交AC于点H,若点G是E2D2的中点,试判断四边形OHE2G的形状,并说明理由.
(1)【解】∵OD1∥AC,∴∠A=∠AOD1=30°.
∵将三角板DOE绕点O顺时针方向旋转α(0°<α<90°)角到三角板D1OE1的位置,∴∠AOD1=α=30°.
【解】(2)四边形OHE2G是正方形,理由如下:
∵∠E2OD2=90°,OD2=OE2,点G是E2D2的中点,
∴E2G=OG,E2G⊥OG.∵OD1∥AC,∠GOH=90°,
∴∠AHO=180°-90°=90°,∴四边形OHE2G是矩形.
又∵E2G=OG,∴四边形OHE2G是正方形.
19.【2023绍兴】如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,E,F分别为垂足,连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
(1)【证明】在正方形ABCD中,AD⊥CD,GE⊥CD,∴∠ADE=∠GEC=90°,
∴AD∥GE,∴∠DAG=∠EGH.
(2)【解】AH⊥EF,理由如下:
连接GC交EF于点O,如图.
在正方形ABCD中,AD=CD,
∵BD为正方形ABCD的对角线,
∴∠ADG=∠CDG=45°.
又∵DG=DG,∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG.
在正方形ABCD中,∠ECF=90°.
又∵GE⊥CD,GF⊥BC,
∴四边形FCEG为矩形,
∴OE=EF,OC=CG,EF=CG,∴OE=OC,
∴∠OEC=∠OCE,∴∠DAG=∠OEC.
由(1)得∠DAG=∠EGH,
∴∠EGH=∠OEC,
∴∠EGH+∠GEH=∠OEC+∠GEH=∠GEC=90°,
∴∠GHE=90°,∴AH⊥EF.
20.【2023天津】如图,在边长为3的正方形ABCD的外侧作等腰三角形ADE,EA=ED=.
(1)△ADE的面积是多少?
(2)若F为BE的中点,连接AF并延长,与CD相交于点G,求AG的长 .
(1)如图,过点E作EM⊥AD于点M.
∵EA=ED=,AD=3,
∴AM=DM=AD=,
∴EM==2,
∴△ADE的面积为AD·EM=×3×2=3.
(2)如图,延长EM交AG于点N,交BC于点P.
∵四边形ABCD是正方形,
∴∠ADC=∠ABC=90°,BC∥AD,AB∥CD,
∴EP⊥BC.
又∵EP⊥AD,
∴四边形ABPM是矩形,
∴PM=AB=3,AB∥EP,
∴EP=5,∠ABF=∠NEF,EP∥CD.
∵F为BE的中点,∴BF=EF,
又∵∠AFB=∠NFE,∴△ABF≌△NEF(ASA),
∴EN=AB=3,∴MN=1.
由PM∥CD,AM=DM,易知AN=NG,
∴MN为△AGD的中位线,
∴GD=2MN=2,
∴AG==.
21.已知四边形ABCD是正方形,△DEF绕点D旋转(DE<AB),∠EDF=90°,DE=DF,连接AE,CF.
(1)如图①,求证:△ADE≌△CDF;
(2)直线AE与CF相交于点G.
①如图②,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图③,连接BG,若AB=4,DE=2,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
(1)【证明】∵四边形ABCD是正方形,∴AD=DC,∠ADC=90°.∵∠EDF=90°,∴∠ADC=∠EDF.
∴∠ADE=∠CDF.
∴△ADE≌△CDF(SAS).
(2)①【证明】如图②,设AG与CD相交于点P.
∵∠ADP=90°,∴∠DAP+∠DPA=90°.
∵△ADE≌△CDF,∴∠DAE=∠DCF.
又∵∠DPA=∠GPC,
∴∠DAE+∠DPA=∠GPC+∠GCP=90°.
∴∠PGN=90°.
又∵BM⊥AG,BN⊥GN,
∴四边形BMGN是矩形.
∴∠MBN=90°.∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°=∠MBN.∴∠ABM=∠CBN.
又∵∠AMB=∠BNC=90°,∴△AMB≌△CNB.
∴MB=NB.
∴矩形BMGN是正方形.
②【解】线段BG长度的最小值为2.
22.如图①,四边形ABCD是正方形,G是CD边上的一个动点(点G与点C,D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)猜想图①中线段BG、线段DE的数量关系及所在直线的位置关系,并说明理由;
(2)将图①中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图②③的情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图②证明你的判断.
(1)【解】BG=DE,BG⊥DE.理由如下:
如图①,延长BG交DE于点H.
∵四边形ABCD和四边形CEFG都是正方形,
∴BC=DC,∠BCG=∠DCE=90°,CG=CE.
∴△BCG≌△DCE.∴BG=DE,∠1=∠2.
∵∠1+∠CGB=90°,∠CGB=∠DGH,∴∠2+∠DGH=90°.∴∠DHG=90°.∴BH⊥DE,即BG⊥DE.
(2)【解】BG=DE,BG⊥DE仍然成立.
证明:如图②,设BG与DE相交于点O,DC与BG相交于点H.∵四边形ABCD、四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG=90°.
∴∠BCG=∠DCE. ∴△BCG≌△DCE.
∴BG=DE,∠CBG=∠CDE.
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°.∴∠DOH=90°.∴BG⊥DE.
