第18章 平行四边形 测试卷(含答案)
图片预览



文档简介
第18章 平行四边形 测试卷
(考试时间:100分钟,赋分:120分)
姓名:________ 班级:________ 分数:________
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案
1.【2023武汉蔡甸区期中】在 ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.1∶1∶2∶2 D.2∶1∶2∶1
2.在△ABC中,点D,E分别是AB,AC的中点.若DE=2,则BC的长是( )
A.3 B.4 C.5 D.6
3.下列命题是假命题的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.正方形的对角线互相垂直平分且相等
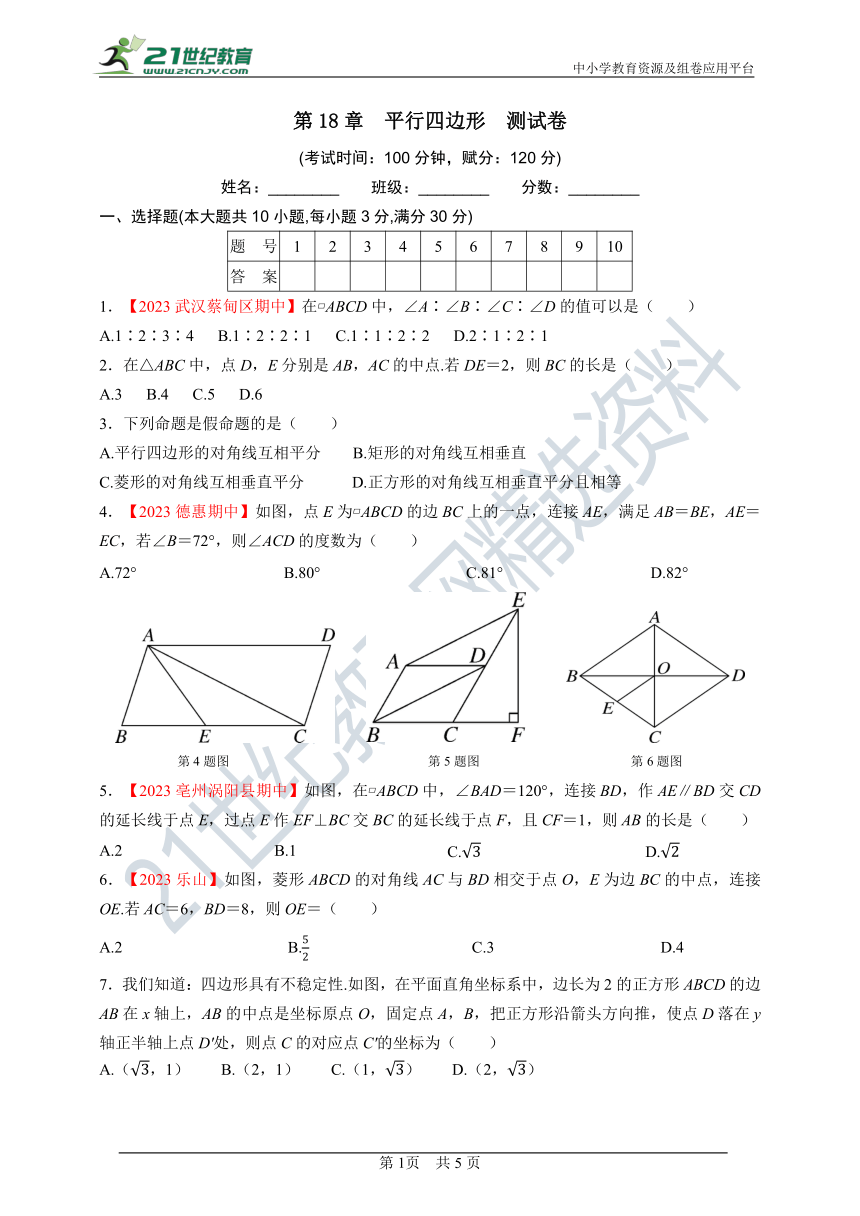
4.【2023德惠期中】如图,点E为 ABCD的边BC上的一点,连接AE,满足AB=BE,AE=EC,若∠B=72°,则∠ACD的度数为( )
A.72° B.80° C.81° D.82°
第4题图 第5题图 第6题图
5.【2023亳州涡阳县期中】如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A.2 B.1 C. D.
6.【2023乐山】如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )
A.2 B. C.3 D.4
7.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D'处,则点C的对应点C'的坐标为( )
A.(,1) B.(2,1) C.(1,) D.(2,)
第7题图 第8题图 第9题图
8.【2023德阳】如图, ABCD的面积为12,AC=BD=6,AC与BD交于点O,分别过点C,D作BD,AC的平行线相交于点F,点G是CD的中点,点P是四边形OCFD边上的动点,则PG的最小值是( )
A.1 B. C. D.3
9.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥AB.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形 B.若AD=EF,则四边形AEDF是矩形
C.若AD⊥EF,则四边形AEDF是菱形 D.若AD⊥BC且AB=AC,则四边形AEDF是正方形
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10 cm,BC=8 cm,点P从点D出发,以1 cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当t=4 s时,四边形ABMP为矩形 B.当t=5 s时,四边形CDPM为平行四边形
C.当CD=PM时,t=4 s D.当CD= PM时,t=4 s或6 s
第10题图 第11题图 第12题图
二、填空题(本大题共8小题,每小题3分,满分24分)
11.如图,已知∠1=∠2,要使四边形ABCD成为平行四边形,还需要添加的条件是 (只需写出一个即可).
12.如图,CD是△ABC的中线,点E,F分别是AC,DC的中点,EF=2,则AB的长为 .
13.【2023·武汉青山区期中】如图,平行四边形ABCD的两条对角线AC,BD相交于点O,且AC+BD=36,若△COD的周长为29,则AB= .
第13题图 第15题图 第16题图
14.【2023·淮南凤台县期中】在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
15.【2023·怀化】如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
16.如图,在矩形ABCD中,E是边AD上一点,点F,G分别是BE,CE的中点,连接AF,DG,FG.若AF=3,DG=4,FG=5,则矩形ABCD的面积为 .
17.如果一个平行四边形的一个内角的平分线分它的一边为1∶2的两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”.当协调边为6时,这个平行四边形的周长为 .
18.【2023·南京外国语学校期中】如图,将边长为2的正方形纸片ABCD沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q,连接PQ,则△GPQ周长的最小值是 .
三、解答题(共66分)
19.(8分)如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连接AE,AF.求证:AE=AF.
20.(8分)如图,在 ABCD中,DF平分∠ADC,交AB于点F,BE∥DF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.
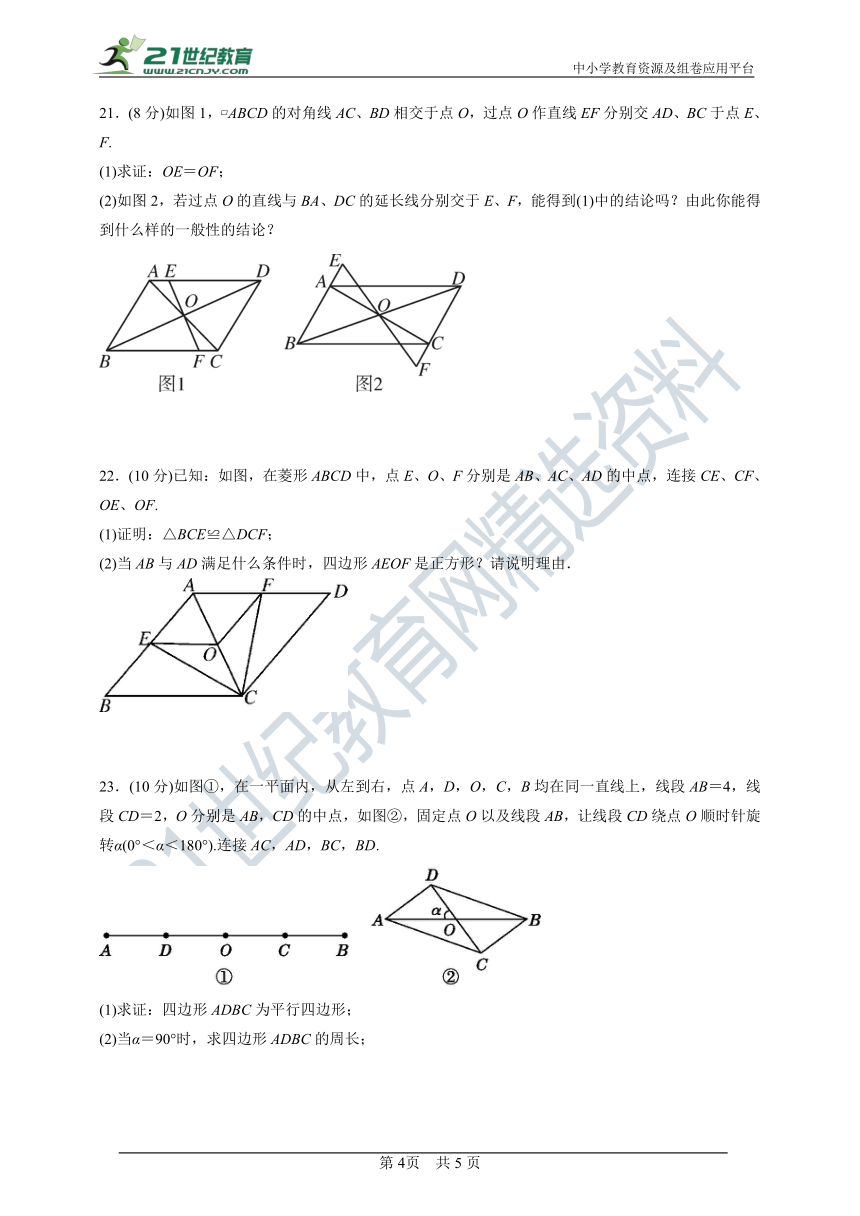
21.(8分)如图1, ABCD的对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F.
(1)求证:OE=OF;
(2)如图2,若过点O的直线与BA、DC的延长线分别交于E、F,能得到(1)中的结论吗?由此你能得到什么样的一般性的结论?
22.(10分)已知:如图,在菱形ABCD中,点E、O、F分别是AB、AC、AD的中点,连接CE、CF、OE、OF.
(1)证明:△BCE≌△DCF;
(2)当AB与AD满足什么条件时,四边形AEOF是正方形?请说明理由.
23.(10分)如图①,在一平面内,从左到右,点A,D,O,C,B均在同一直线上,线段AB=4,线段CD=2,O分别是AB,CD的中点,如图②,固定点O以及线段AB,让线段CD绕点O顺时针旋转α(0°<α<180°).连接AC,AD,BC,BD.
(1)求证:四边形ADBC为平行四边形;
(2)当α=90°时,求四边形ADBC的周长;
24.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB的中点时,判断四边形BECD的形状,并说明理由;
(3)若D为AB的中点,则当∠A满足什么条件时,四边形BECD是正方形?
25.(12分)已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG.当点E在线段BC上时,如图①,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图②),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图③),直接写出AB,CG,CE之间的关系.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第5页 共5页
参考答案
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 D B B C B B D A D D
1.【2023武汉蔡甸区期中】在 ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( D )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.1∶1∶2∶2 D.2∶1∶2∶1
2.在△ABC中,点D,E分别是AB,AC的中点.若DE=2,则BC的长是( B )
A.3 B.4 C.5 D.6
3.下列命题是假命题的是( B )
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.正方形的对角线互相垂直平分且相等
4.【2023德惠期中】如图,点E为 ABCD的边BC上的一点,连接AE,满足AB=BE,AE=EC,若∠B=72°,则∠ACD的度数为( C )
A.72° B.80° C.81° D.82°
第4题图 第5题图 第6题图
5.【2023亳州涡阳县期中】如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( B )
A.2 B.1 C. D.
6.【2023乐山】如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( B )
A.2 B. C.3 D.4
7.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D'处,则点C的对应点C'的坐标为( D )
A.(,1) B.(2,1) C.(1,) D.(2,)
第7题图 第8题图 第9题图
8.【2023德阳】如图, ABCD的面积为12,AC=BD=6,AC与BD交于点O,分别过点C,D作BD,AC的平行线相交于点F,点G是CD的中点,点P是四边形OCFD边上的动点,则PG的最小值是( A )
A.1 B. C. D.3
9.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥AB.下列四个判断中,不正确的是( D )
A.四边形AEDF是平行四边形 B.若AD=EF,则四边形AEDF是矩形
C.若AD⊥EF,则四边形AEDF是菱形 D.若AD⊥BC且AB=AC,则四边形AEDF是正方形
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10 cm,BC=8 cm,点P从点D出发,以1 cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( D )
A.当t=4 s时,四边形ABMP为矩形 B.当t=5 s时,四边形CDPM为平行四边形
C.当CD=PM时,t=4 s D.当CD= PM时,t=4 s或6 s
第10题图 第11题图 第12题图
二、填空题(本大题共8小题,每小题3分,满分24分)
11.如图,已知∠1=∠2,要使四边形ABCD成为平行四边形,还需要添加的条件是 (只需写出一个即可).
【答案】AD=BC(答案不唯一)
12.如图,CD是△ABC的中线,点E,F分别是AC,DC的中点,EF=2,则AB的长为 .
【答案】8
13.【2023·武汉青山区期中】如图,平行四边形ABCD的两条对角线AC,BD相交于点O,且AC+BD=36,若△COD的周长为29,则AB= .
【答案】11
第13题图 第15题图 第16题图
14.【2023·淮南凤台县期中】在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
【答案】8或3
15.【2023·怀化】如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
【答案】3
16.如图,在矩形ABCD中,E是边AD上一点,点F,G分别是BE,CE的中点,连接AF,DG,FG.若AF=3,DG=4,FG=5,则矩形ABCD的面积为 .
【答案】48
17.如果一个平行四边形的一个内角的平分线分它的一边为1∶2的两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”.当协调边为6时,这个平行四边形的周长为 .
【答案】16或20
18.【2023·南京外国语学校期中】如图,将边长为2的正方形纸片ABCD沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q,连接PQ,则△GPQ周长的最小值是 .
【答案】+1
三、解答题(共66分)
19.(8分)如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连接AE,AF.求证:AE=AF.
证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
∵BE=DF,∴△ABE≌△ADF(SAS).
∴AE=AF.
20.(8分)如图,在 ABCD中,DF平分∠ADC,交AB于点F,BE∥DF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.
解:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠A+∠ADC=180°.
∵∠A=40°,∴∠ADC=140°.
∵DF平分∠ADC,∴∠CDF=∠ADC=70°.
∴∠AFD=∠CDF=70°.
∵DF∥BE,∴∠ABE=∠AFD=70°.
21.(8分)如图1, ABCD的对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F.
(1)求证:OE=OF;
(2)如图2,若过点O的直线与BA、DC的延长线分别交于E、F,能得到(1)中的结论吗?由此你能得到什么样的一般性的结论?
(1)证明:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF;
(2)解:能得到(1)中的结论.∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF.一般性的结论是:过平行四边形的对角线的交点O作一条直线与平行四边形相对的边或延长线相交于E、F两点,则OE=OF.
22.(10分)已知:如图,在菱形ABCD中,点E、O、F分别是AB、AC、AD的中点,连接CE、CF、OE、OF.
(1)证明:△BCE≌△DCF;
(2)当AB与AD满足什么条件时,四边形AEOF是正方形?请说明理由.
(1)证明:∵四边形ABCD为菱形,∴AB=BC=CD=DA,∠B=∠D.又E、F分别是AB、AD的中点,∴BE=DF,∴△BCE≌△DCF(SAS);
(2)解:若AB⊥AD,则四边形AEOF为正方形,理由如下:∵E、O分别是AB、AC的中点,∴EO∥BC,又BC∥AD,∴OE∥AD,即OE∥AF,同理可证:OF∥AE,所以四边形AEOF为平行四边形,由(1)可得AE=AF,所以平行四边形AEOF为菱形,因为AD⊥AB,所以∠BAD=90°,所以菱形AEOF为正方形.
23.(10分)如图①,在一平面内,从左到右,点A,D,O,C,B均在同一直线上,线段AB=4,线段CD=2,O分别是AB,CD的中点,如图②,固定点O以及线段AB,让线段CD绕点O顺时针旋转α(0°<α<180°).连接AC,AD,BC,BD.
(1)求证:四边形ADBC为平行四边形;
(2)当α=90°时,求四边形ADBC的周长;
(1)【证明】∵O分别是AB,CD的中点,
∴OA=OB,OC=OD.
∴四边形ADBC为平行四边形.
(2)【解】∵α=90°,∴AB⊥CD.
又∵四边形ADBC为平行四边形,∴四边形ADBC为菱形.
∵AB=4,CD=2,∴OA=2,OD=1.
∴AD===.
∴四边形ADBC的周长为4.
24.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB的中点时,判断四边形BECD的形状,并说明理由;
(3)若D为AB的中点,则当∠A满足什么条件时,四边形BECD是正方形?
(1)证明:∵DE⊥BC,
∴∠DFB=90°.
∵∠ACB=90°,
∴∠ACB=∠DFB.∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形.∴CE=AD.
(2)解:四边形BECD是菱形.理由如下:
∵D为AB的中点,∴AD=BD.
∵CE=AD,∴BD=CE.
∵BD∥CE,∴四边形BECD是平行四边形.
∵∠ACB=90°,D为AB的中点,∴CD=BD.
∴四边形BECD是菱形.
(3)解:当∠A=45°时,四边形BECD是正方形.
∵∠ACB=90°,∠A=45°,∴∠ABC=45°.
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°.∴∠DBE=90°.
∴四边形BECD是正方形.
25.(12分)已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG.当点E在线段BC上时,如图①,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图②),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图③),直接写出AB,CG,CE之间的关系.
【解】(1)AB=CG-CE.证明如下:
∵四边形ABCD是菱形,∴AB=BC.
又∵∠BAC=60°,∴△ABC是等边三角形.
∴AB=AC.
∵∠EAG=60°,∴∠BAC=∠EAG.
∴∠BAC+∠CAE=∠EAG+∠CAE,
即∠BAE=∠CAG.又∵四边形AEFG是菱形,∴AE=AG.
在△ABE和△ACG中,∴△ABE≌△ACG(SAS).∴BE=CG.
∵AB=BC=BE-CE,∴AB=CG-CE.
(2)AB=CE-CG.
21世纪教育网版权所有
(考试时间:100分钟,赋分:120分)
姓名:________ 班级:________ 分数:________
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案
1.【2023武汉蔡甸区期中】在 ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.1∶1∶2∶2 D.2∶1∶2∶1
2.在△ABC中,点D,E分别是AB,AC的中点.若DE=2,则BC的长是( )
A.3 B.4 C.5 D.6
3.下列命题是假命题的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.正方形的对角线互相垂直平分且相等
4.【2023德惠期中】如图,点E为 ABCD的边BC上的一点,连接AE,满足AB=BE,AE=EC,若∠B=72°,则∠ACD的度数为( )
A.72° B.80° C.81° D.82°
第4题图 第5题图 第6题图
5.【2023亳州涡阳县期中】如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A.2 B.1 C. D.
6.【2023乐山】如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )
A.2 B. C.3 D.4
7.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D'处,则点C的对应点C'的坐标为( )
A.(,1) B.(2,1) C.(1,) D.(2,)
第7题图 第8题图 第9题图
8.【2023德阳】如图, ABCD的面积为12,AC=BD=6,AC与BD交于点O,分别过点C,D作BD,AC的平行线相交于点F,点G是CD的中点,点P是四边形OCFD边上的动点,则PG的最小值是( )
A.1 B. C. D.3
9.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥AB.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形 B.若AD=EF,则四边形AEDF是矩形
C.若AD⊥EF,则四边形AEDF是菱形 D.若AD⊥BC且AB=AC,则四边形AEDF是正方形
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10 cm,BC=8 cm,点P从点D出发,以1 cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当t=4 s时,四边形ABMP为矩形 B.当t=5 s时,四边形CDPM为平行四边形
C.当CD=PM时,t=4 s D.当CD= PM时,t=4 s或6 s
第10题图 第11题图 第12题图
二、填空题(本大题共8小题,每小题3分,满分24分)
11.如图,已知∠1=∠2,要使四边形ABCD成为平行四边形,还需要添加的条件是 (只需写出一个即可).
12.如图,CD是△ABC的中线,点E,F分别是AC,DC的中点,EF=2,则AB的长为 .
13.【2023·武汉青山区期中】如图,平行四边形ABCD的两条对角线AC,BD相交于点O,且AC+BD=36,若△COD的周长为29,则AB= .
第13题图 第15题图 第16题图
14.【2023·淮南凤台县期中】在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
15.【2023·怀化】如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
16.如图,在矩形ABCD中,E是边AD上一点,点F,G分别是BE,CE的中点,连接AF,DG,FG.若AF=3,DG=4,FG=5,则矩形ABCD的面积为 .
17.如果一个平行四边形的一个内角的平分线分它的一边为1∶2的两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”.当协调边为6时,这个平行四边形的周长为 .
18.【2023·南京外国语学校期中】如图,将边长为2的正方形纸片ABCD沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q,连接PQ,则△GPQ周长的最小值是 .
三、解答题(共66分)
19.(8分)如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连接AE,AF.求证:AE=AF.
20.(8分)如图,在 ABCD中,DF平分∠ADC,交AB于点F,BE∥DF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.
21.(8分)如图1, ABCD的对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F.
(1)求证:OE=OF;
(2)如图2,若过点O的直线与BA、DC的延长线分别交于E、F,能得到(1)中的结论吗?由此你能得到什么样的一般性的结论?
22.(10分)已知:如图,在菱形ABCD中,点E、O、F分别是AB、AC、AD的中点,连接CE、CF、OE、OF.
(1)证明:△BCE≌△DCF;
(2)当AB与AD满足什么条件时,四边形AEOF是正方形?请说明理由.
23.(10分)如图①,在一平面内,从左到右,点A,D,O,C,B均在同一直线上,线段AB=4,线段CD=2,O分别是AB,CD的中点,如图②,固定点O以及线段AB,让线段CD绕点O顺时针旋转α(0°<α<180°).连接AC,AD,BC,BD.
(1)求证:四边形ADBC为平行四边形;
(2)当α=90°时,求四边形ADBC的周长;
24.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB的中点时,判断四边形BECD的形状,并说明理由;
(3)若D为AB的中点,则当∠A满足什么条件时,四边形BECD是正方形?
25.(12分)已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG.当点E在线段BC上时,如图①,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图②),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图③),直接写出AB,CG,CE之间的关系.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第5页 共5页
参考答案
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 D B B C B B D A D D
1.【2023武汉蔡甸区期中】在 ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( D )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.1∶1∶2∶2 D.2∶1∶2∶1
2.在△ABC中,点D,E分别是AB,AC的中点.若DE=2,则BC的长是( B )
A.3 B.4 C.5 D.6
3.下列命题是假命题的是( B )
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.正方形的对角线互相垂直平分且相等
4.【2023德惠期中】如图,点E为 ABCD的边BC上的一点,连接AE,满足AB=BE,AE=EC,若∠B=72°,则∠ACD的度数为( C )
A.72° B.80° C.81° D.82°
第4题图 第5题图 第6题图
5.【2023亳州涡阳县期中】如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( B )
A.2 B.1 C. D.
6.【2023乐山】如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( B )
A.2 B. C.3 D.4
7.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D'处,则点C的对应点C'的坐标为( D )
A.(,1) B.(2,1) C.(1,) D.(2,)
第7题图 第8题图 第9题图
8.【2023德阳】如图, ABCD的面积为12,AC=BD=6,AC与BD交于点O,分别过点C,D作BD,AC的平行线相交于点F,点G是CD的中点,点P是四边形OCFD边上的动点,则PG的最小值是( A )
A.1 B. C. D.3
9.如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥AB.下列四个判断中,不正确的是( D )
A.四边形AEDF是平行四边形 B.若AD=EF,则四边形AEDF是矩形
C.若AD⊥EF,则四边形AEDF是菱形 D.若AD⊥BC且AB=AC,则四边形AEDF是正方形
10.如图,在四边形ABCD中,∠A=∠B=90°,AD=10 cm,BC=8 cm,点P从点D出发,以1 cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( D )
A.当t=4 s时,四边形ABMP为矩形 B.当t=5 s时,四边形CDPM为平行四边形
C.当CD=PM时,t=4 s D.当CD= PM时,t=4 s或6 s
第10题图 第11题图 第12题图
二、填空题(本大题共8小题,每小题3分,满分24分)
11.如图,已知∠1=∠2,要使四边形ABCD成为平行四边形,还需要添加的条件是 (只需写出一个即可).
【答案】AD=BC(答案不唯一)
12.如图,CD是△ABC的中线,点E,F分别是AC,DC的中点,EF=2,则AB的长为 .
【答案】8
13.【2023·武汉青山区期中】如图,平行四边形ABCD的两条对角线AC,BD相交于点O,且AC+BD=36,若△COD的周长为29,则AB= .
【答案】11
第13题图 第15题图 第16题图
14.【2023·淮南凤台县期中】在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
【答案】8或3
15.【2023·怀化】如图,点P是正方形ABCD的对角线AC上的一点,PE⊥AD于点E,PE=3,则点P到直线AB的距离为 .
【答案】3
16.如图,在矩形ABCD中,E是边AD上一点,点F,G分别是BE,CE的中点,连接AF,DG,FG.若AF=3,DG=4,FG=5,则矩形ABCD的面积为 .
【答案】48
17.如果一个平行四边形的一个内角的平分线分它的一边为1∶2的两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”.当协调边为6时,这个平行四边形的周长为 .
【答案】16或20
18.【2023·南京外国语学校期中】如图,将边长为2的正方形纸片ABCD沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q,连接PQ,则△GPQ周长的最小值是 .
【答案】+1
三、解答题(共66分)
19.(8分)如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连接AE,AF.求证:AE=AF.
证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
∵BE=DF,∴△ABE≌△ADF(SAS).
∴AE=AF.
20.(8分)如图,在 ABCD中,DF平分∠ADC,交AB于点F,BE∥DF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.
解:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠A+∠ADC=180°.
∵∠A=40°,∴∠ADC=140°.
∵DF平分∠ADC,∴∠CDF=∠ADC=70°.
∴∠AFD=∠CDF=70°.
∵DF∥BE,∴∠ABE=∠AFD=70°.
21.(8分)如图1, ABCD的对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F.
(1)求证:OE=OF;
(2)如图2,若过点O的直线与BA、DC的延长线分别交于E、F,能得到(1)中的结论吗?由此你能得到什么样的一般性的结论?
(1)证明:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF;
(2)解:能得到(1)中的结论.∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠EAO=∠FCO,∠AEO=∠CFO,∴△AEO≌△CFO(AAS),∴OE=OF.一般性的结论是:过平行四边形的对角线的交点O作一条直线与平行四边形相对的边或延长线相交于E、F两点,则OE=OF.
22.(10分)已知:如图,在菱形ABCD中,点E、O、F分别是AB、AC、AD的中点,连接CE、CF、OE、OF.
(1)证明:△BCE≌△DCF;
(2)当AB与AD满足什么条件时,四边形AEOF是正方形?请说明理由.
(1)证明:∵四边形ABCD为菱形,∴AB=BC=CD=DA,∠B=∠D.又E、F分别是AB、AD的中点,∴BE=DF,∴△BCE≌△DCF(SAS);
(2)解:若AB⊥AD,则四边形AEOF为正方形,理由如下:∵E、O分别是AB、AC的中点,∴EO∥BC,又BC∥AD,∴OE∥AD,即OE∥AF,同理可证:OF∥AE,所以四边形AEOF为平行四边形,由(1)可得AE=AF,所以平行四边形AEOF为菱形,因为AD⊥AB,所以∠BAD=90°,所以菱形AEOF为正方形.
23.(10分)如图①,在一平面内,从左到右,点A,D,O,C,B均在同一直线上,线段AB=4,线段CD=2,O分别是AB,CD的中点,如图②,固定点O以及线段AB,让线段CD绕点O顺时针旋转α(0°<α<180°).连接AC,AD,BC,BD.
(1)求证:四边形ADBC为平行四边形;
(2)当α=90°时,求四边形ADBC的周长;
(1)【证明】∵O分别是AB,CD的中点,
∴OA=OB,OC=OD.
∴四边形ADBC为平行四边形.
(2)【解】∵α=90°,∴AB⊥CD.
又∵四边形ADBC为平行四边形,∴四边形ADBC为菱形.
∵AB=4,CD=2,∴OA=2,OD=1.
∴AD===.
∴四边形ADBC的周长为4.
24.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB的中点时,判断四边形BECD的形状,并说明理由;
(3)若D为AB的中点,则当∠A满足什么条件时,四边形BECD是正方形?
(1)证明:∵DE⊥BC,
∴∠DFB=90°.
∵∠ACB=90°,
∴∠ACB=∠DFB.∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形.∴CE=AD.
(2)解:四边形BECD是菱形.理由如下:
∵D为AB的中点,∴AD=BD.
∵CE=AD,∴BD=CE.
∵BD∥CE,∴四边形BECD是平行四边形.
∵∠ACB=90°,D为AB的中点,∴CD=BD.
∴四边形BECD是菱形.
(3)解:当∠A=45°时,四边形BECD是正方形.
∵∠ACB=90°,∠A=45°,∴∠ABC=45°.
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°.∴∠DBE=90°.
∴四边形BECD是正方形.
25.(12分)已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG.当点E在线段BC上时,如图①,易证:AB=CG+CE.
(1)当点E在线段BC的延长线上时(如图②),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图③),直接写出AB,CG,CE之间的关系.
【解】(1)AB=CG-CE.证明如下:
∵四边形ABCD是菱形,∴AB=BC.
又∵∠BAC=60°,∴△ABC是等边三角形.
∴AB=AC.
∵∠EAG=60°,∴∠BAC=∠EAG.
∴∠BAC+∠CAE=∠EAG+∠CAE,
即∠BAE=∠CAG.又∵四边形AEFG是菱形,∴AE=AG.
在△ABE和△ACG中,∴△ABE≌△ACG(SAS).∴BE=CG.
∵AB=BC=BE-CE,∴AB=CG-CE.
(2)AB=CE-CG.
21世纪教育网版权所有
