第18章 平行四边形 章末复习(含答案)
文档属性
| 名称 | 第18章 平行四边形 章末复习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 00:00:00 | ||
图片预览

文档简介
第18章 平行四边形 章末复习
【知识网络】
【考点突破】
考点1:平行四边形的性质与判定
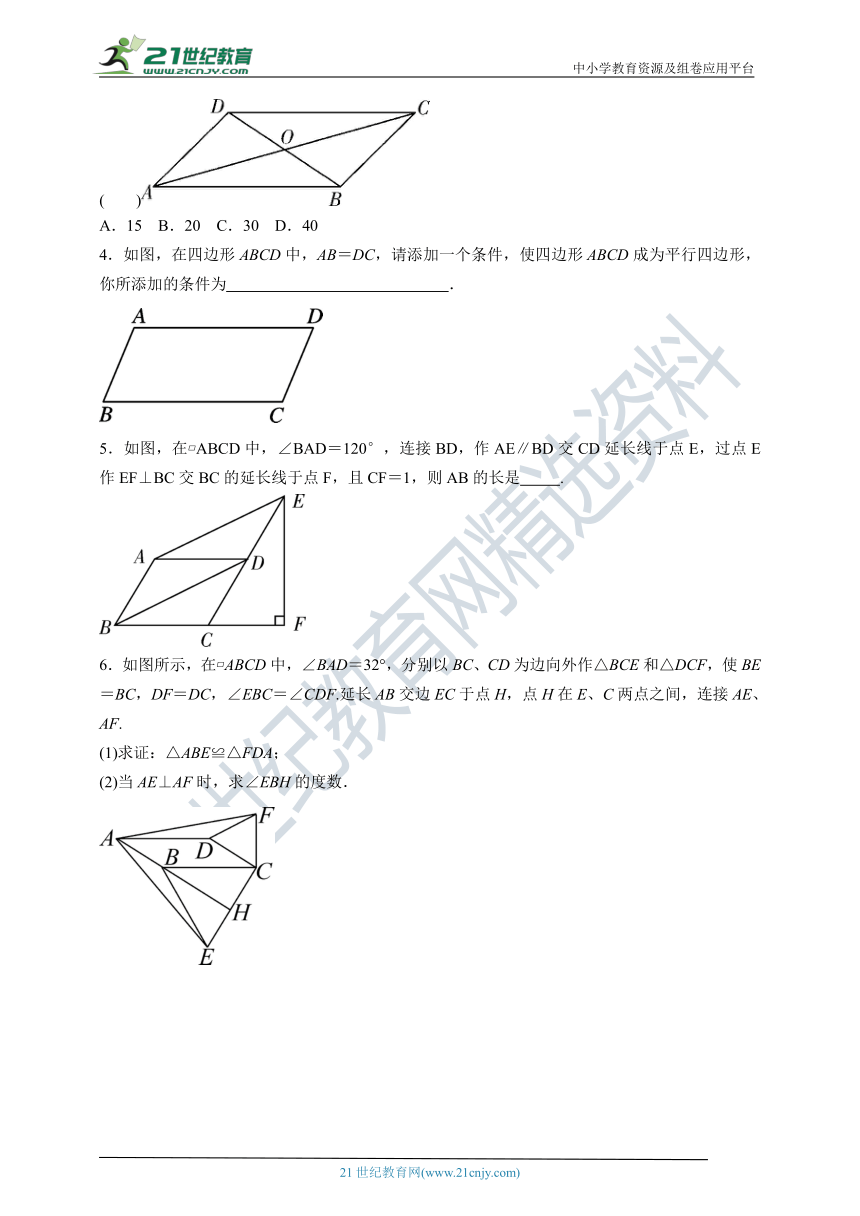
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件中不能判定这个四边形是平行四边形的是( )
A.AB∥CD,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
2.如图,在 ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( )
A.61° B.109° C.119° D.122°
3.如图,△AOB与△AOD周长之差为5,且AB∶AD=2∶1,则 ABCD的周长是( )
A.15 B.20 C.30 D.40
4.如图,在四边形ABCD中,AB=DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为 .
5.如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 .
6.如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
7.如图,在 ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形.
(2)若AF=12,EM=5,求AN的长.
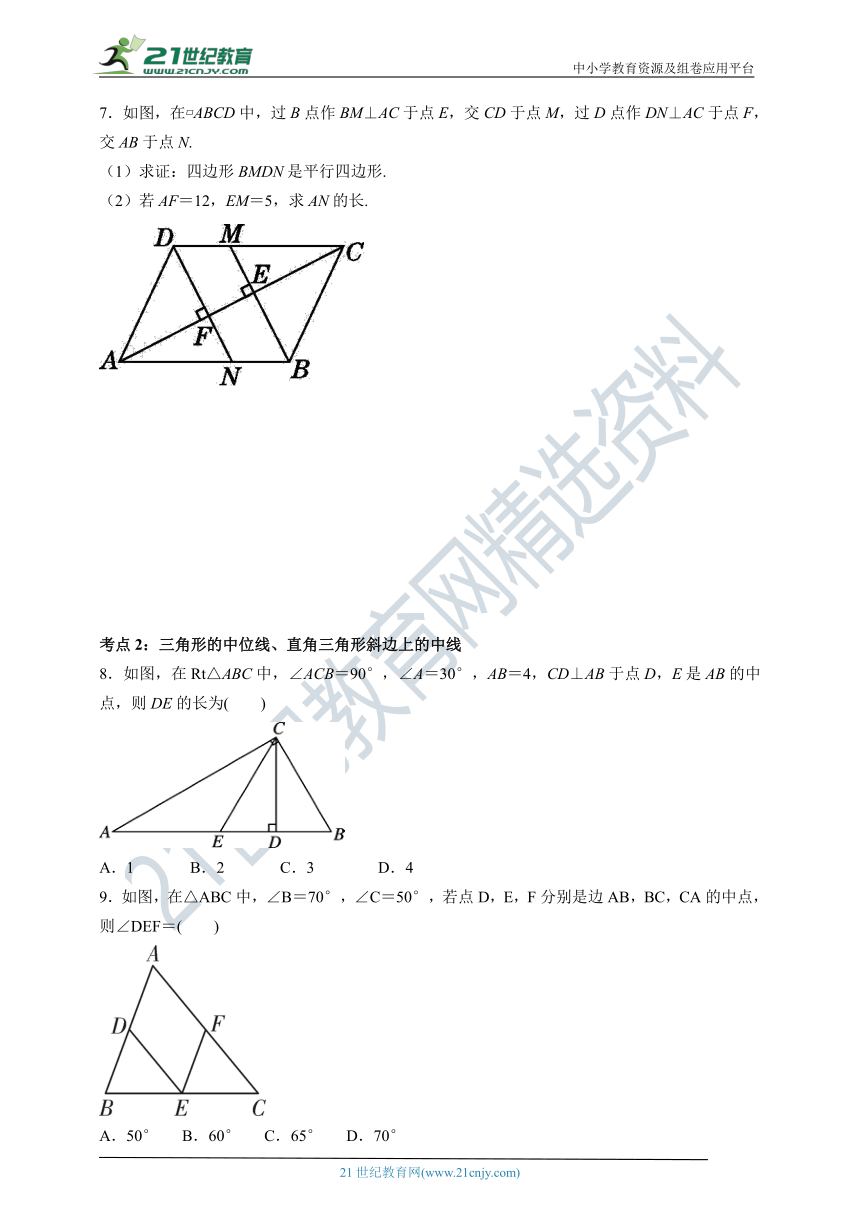
考点2:三角形的中位线、直角三角形斜边上的中线
8.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的中点,则DE的长为( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠B=70°,∠C=50°,若点D,E,F分别是边AB,BC,CA的中点,则∠DEF=( )
A.50° B.60° C.65° D.70°
10.如图,在△ABC中,D,E分别是AB,AC的中点,G是BC上一点,连接DE,DG,GE,F是DE的中点,连接GF,若DG⊥EG,GF=3,则BC的长为( )
A.12 B.16 C.18 D.6
11.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,若△DEF的周长为10,则△ABC的周长为 .
12.如图,在△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F.若BC=6,则DF的长为 .
13.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
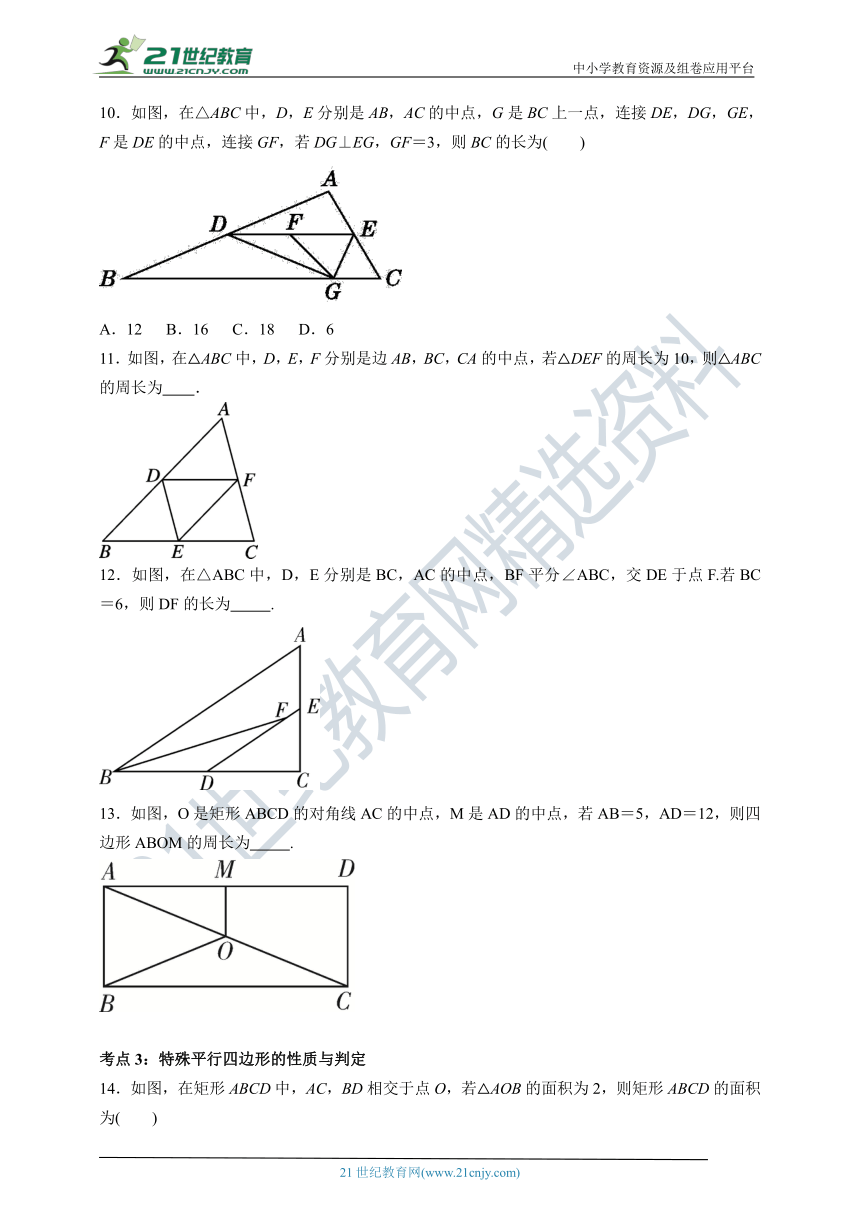
考点3:特殊平行四边形的性质与判定
14.如图,在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
15.如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为( )
A.(2,2) B.(,2) C.(3,) D.(2,)
16.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,连接OE,则下列结论中不一定正确的是( )
A.AB=AD B.OE=AB C.∠DOE=∠DEO D.∠EOD=∠EDO
17.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
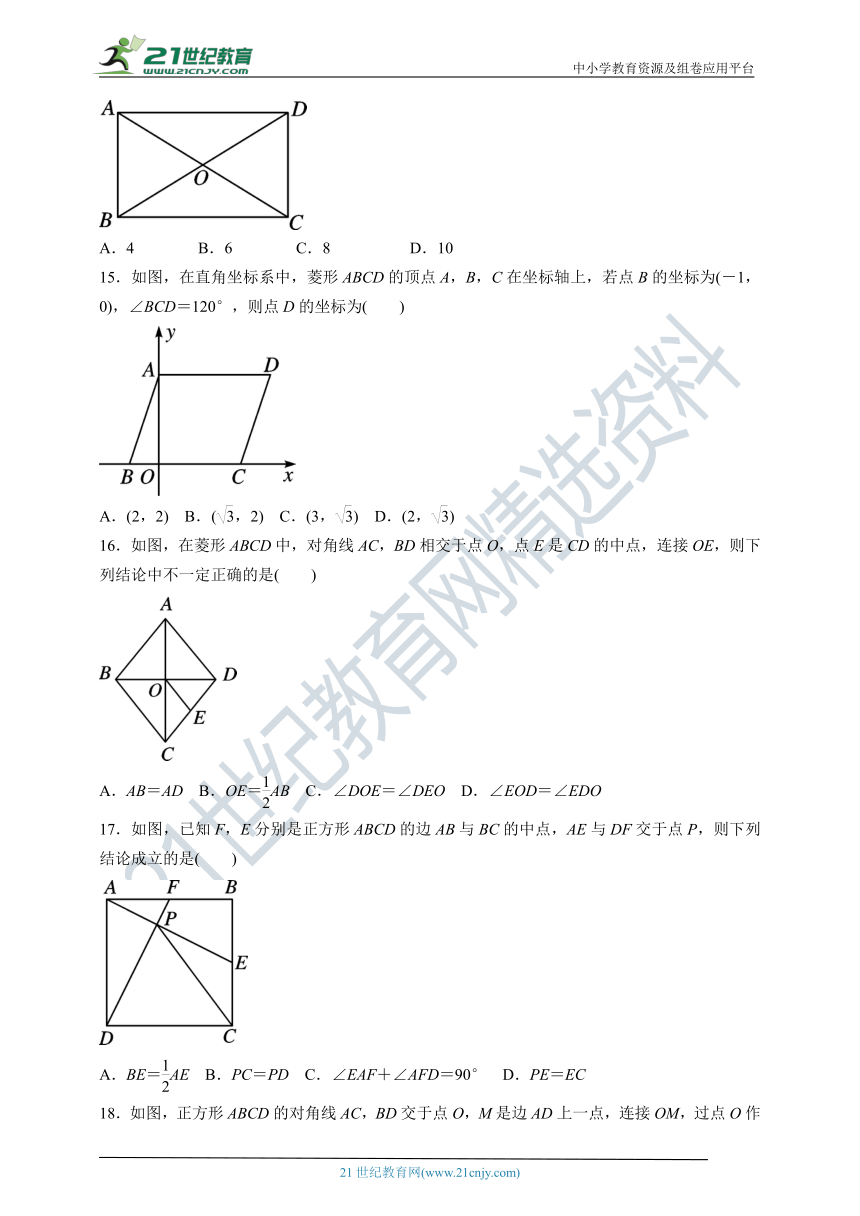
18.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 ,使平行四边形ABCD是矩形.
20.由沈康身教授所著、数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分),则图中AB的长应是 .
21.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.在平面内有一个正方形,边长为2,中心为O,在正方形外有一点P,OP=2,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
22.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.
求证:四边形AEDF是菱形.
23.如图,正方形ABCD的对角线相交于点O,E是正方形外部一点,以OE为边作正方形OEFG,OE与AB相交于点M,OG与BC相交于点N,若AB=6,OE=5,求四边形OMBN的面积 .
24.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
(1)求证:四边形EDFG是正方形;
(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【知识网络】
【考点突破】
考点1:平行四边形的性质与判定
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件中不能判定这个四边形是平行四边形的是( D )
A.AB∥CD,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
2.如图,在 ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( C )
A.61° B.109° C.119° D.122°
3.如图,△AOB与△AOD周长之差为5,且AB∶AD=2∶1,则 ABCD的周长是( C )
A.15 B.20 C.30 D.40
4.如图,在四边形ABCD中,AB=DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为 .
【答案】AB∥DC(答案不唯一)
5.如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 .
【答案】1
6.如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
(1)∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,AD=BC=BE,DF=DC=AB.在△ABE和△FDA中,AB=FD,BE=DA,∠ABE=360°-∠ABC-∠EBC=360°-∠ADC-∠CDF=∠ADF,∴△ABE≌△FDA(SAS);
(2)由(1)得∠AEB=∠FAD,∴∠EBH=∠AEB+∠EAB=∠EAB+∠FAD=90°-∠BAD=90°-32°=58°,即∠EBH=58°.
7.如图,在 ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形.
(2)若AF=12,EM=5,求AN的长.
(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB.∵BM⊥AC,DN⊥AC,∴DN∥BM.
∴四边形BMDN是平行四边形.
(2)解:∵四边形BMDN是平行四边形,∴DM=BN.
∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB.
∴CM=AN,∠MCE=∠NAF.
又∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN(AAS).
∴FN=EM=5.
∴在Rt△AFN中,AN===13.
考点2:三角形的中位线、直角三角形斜边上的中线
8.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的中点,则DE的长为( A )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠B=70°,∠C=50°,若点D,E,F分别是边AB,BC,CA的中点,则∠DEF=( B )
A.50° B.60° C.65° D.70°
10.如图,在△ABC中,D,E分别是AB,AC的中点,G是BC上一点,连接DE,DG,GE,F是DE的中点,连接GF,若DG⊥EG,GF=3,则BC的长为( A )
A.12 B.16 C.18 D.6
11.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,若△DEF的周长为10,则△ABC的周长为 .
【答案】20
12.如图,在△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F.若BC=6,则DF的长为 .
【答案】3
13.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
【答案】20
考点3:特殊平行四边形的性质与判定
14.如图,在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( C )
A.4 B.6 C.8 D.10
15.如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为( D )
A.(2,2) B.(,2) C.(3,) D.(2,)
16.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,连接OE,则下列结论中不一定正确的是( C )
A.AB=AD B.OE=AB C.∠DOE=∠DEO D.∠EOD=∠EDO
17.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( C )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
18.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( C )
A.1 B. C.2 D.2
19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 ,使平行四边形ABCD是矩形.
【答案】∠ABC=90°(答案不唯一)
20.由沈康身教授所著、数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分),则图中AB的长应是 .
【答案】-1
21.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.在平面内有一个正方形,边长为2,中心为O,在正方形外有一点P,OP=2,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
【答案】2-≤d≤1
22.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.
求证:四边形AEDF是菱形.
证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠C,
AD∥BC,AB∥CD,
∵AF∥ED,∴四边形AEDF是平行四边形,
∵AD∥BC,∴∠DGC=∠ADE,
∵DG=DC,∴∠DGC=∠C,
∴∠BAD=∠ADE,∴AE=DE,
∴平行四边形AEDF是菱形.
23.如图,正方形ABCD的对角线相交于点O,E是正方形外部一点,以OE为边作正方形OEFG,OE与AB相交于点M,OG与BC相交于点N,若AB=6,OE=5,求四边形OMBN的面积 .
解:如图,过点O作OI⊥AB于点I,过点O作OH⊥BC于点H,
∴∠MIO=∠OIB=∠OHN=90°.∵在正方形ABCD中,∠ABC=90°,∠ABO=45°,∴四边形OIBH为矩形,∠BOI=45°=∠ABO. ∴BI=OI.∴四边形OIBH为正方形.∴OI=OH,∠IOH=90°.∴∠ION+∠HON=90°.∵∠EOG=90°,
∴∠MOI+∠ION=90°,∴∠MOI=∠NOH.
在△MOI与△NOH中,
∴△MOI≌△NOH(ASA).
∴四边形OMBN的面积等于正方形OIBH的面积.
由AB=6易得BI=3,∴正方形OIBH的面积为9,
即四边形OMBN的面积为9.
24.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
(1)求证:四边形EDFG是正方形;
(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.
(1)证明:连接CD,∵△ABC为等腰直角三角形,∠ACB=90°,
D是AB的中点,∴∠A=∠DCF=45°,AD=CD.
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,
∴△EDF为等腰直角三角形.∵O为EF的中点,GO=OD,∴GD⊥EF,
且GD=2OD=EF,∴四边形EDFG是正方形.
(2)解:过点D作DE′⊥AC于点E′.
∵△ABC为等腰直角三角形,∠ACB=90°,
AC=BC=4,∴DE′=BC=2,
AB==4.∵点E′为AC的中点,
∴2≤DE<2(点E与点E′重合时取等号),∴4≤S四边形EDFG=DE2<8,
∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.
【知识网络】
【考点突破】
考点1:平行四边形的性质与判定
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件中不能判定这个四边形是平行四边形的是( )
A.AB∥CD,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
2.如图,在 ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( )
A.61° B.109° C.119° D.122°
3.如图,△AOB与△AOD周长之差为5,且AB∶AD=2∶1,则 ABCD的周长是( )
A.15 B.20 C.30 D.40
4.如图,在四边形ABCD中,AB=DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为 .
5.如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 .
6.如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
7.如图,在 ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形.
(2)若AF=12,EM=5,求AN的长.
考点2:三角形的中位线、直角三角形斜边上的中线
8.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的中点,则DE的长为( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠B=70°,∠C=50°,若点D,E,F分别是边AB,BC,CA的中点,则∠DEF=( )
A.50° B.60° C.65° D.70°
10.如图,在△ABC中,D,E分别是AB,AC的中点,G是BC上一点,连接DE,DG,GE,F是DE的中点,连接GF,若DG⊥EG,GF=3,则BC的长为( )
A.12 B.16 C.18 D.6
11.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,若△DEF的周长为10,则△ABC的周长为 .
12.如图,在△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F.若BC=6,则DF的长为 .
13.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
考点3:特殊平行四边形的性质与判定
14.如图,在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
15.如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为( )
A.(2,2) B.(,2) C.(3,) D.(2,)
16.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,连接OE,则下列结论中不一定正确的是( )
A.AB=AD B.OE=AB C.∠DOE=∠DEO D.∠EOD=∠EDO
17.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
18.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 ,使平行四边形ABCD是矩形.
20.由沈康身教授所著、数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分),则图中AB的长应是 .
21.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.在平面内有一个正方形,边长为2,中心为O,在正方形外有一点P,OP=2,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
22.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.
求证:四边形AEDF是菱形.
23.如图,正方形ABCD的对角线相交于点O,E是正方形外部一点,以OE为边作正方形OEFG,OE与AB相交于点M,OG与BC相交于点N,若AB=6,OE=5,求四边形OMBN的面积 .
24.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
(1)求证:四边形EDFG是正方形;
(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【知识网络】
【考点突破】
考点1:平行四边形的性质与判定
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件中不能判定这个四边形是平行四边形的是( D )
A.AB∥CD,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
2.如图,在 ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( C )
A.61° B.109° C.119° D.122°
3.如图,△AOB与△AOD周长之差为5,且AB∶AD=2∶1,则 ABCD的周长是( C )
A.15 B.20 C.30 D.40
4.如图,在四边形ABCD中,AB=DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为 .
【答案】AB∥DC(答案不唯一)
5.如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 .
【答案】1
6.如图所示,在 ABCD中,∠BAD=32°,分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E、C两点之间,连接AE、AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数.
(1)∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,AD=BC=BE,DF=DC=AB.在△ABE和△FDA中,AB=FD,BE=DA,∠ABE=360°-∠ABC-∠EBC=360°-∠ADC-∠CDF=∠ADF,∴△ABE≌△FDA(SAS);
(2)由(1)得∠AEB=∠FAD,∴∠EBH=∠AEB+∠EAB=∠EAB+∠FAD=90°-∠BAD=90°-32°=58°,即∠EBH=58°.
7.如图,在 ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形.
(2)若AF=12,EM=5,求AN的长.
(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB.∵BM⊥AC,DN⊥AC,∴DN∥BM.
∴四边形BMDN是平行四边形.
(2)解:∵四边形BMDN是平行四边形,∴DM=BN.
∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB.
∴CM=AN,∠MCE=∠NAF.
又∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN(AAS).
∴FN=EM=5.
∴在Rt△AFN中,AN===13.
考点2:三角形的中位线、直角三角形斜边上的中线
8.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的中点,则DE的长为( A )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠B=70°,∠C=50°,若点D,E,F分别是边AB,BC,CA的中点,则∠DEF=( B )
A.50° B.60° C.65° D.70°
10.如图,在△ABC中,D,E分别是AB,AC的中点,G是BC上一点,连接DE,DG,GE,F是DE的中点,连接GF,若DG⊥EG,GF=3,则BC的长为( A )
A.12 B.16 C.18 D.6
11.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,若△DEF的周长为10,则△ABC的周长为 .
【答案】20
12.如图,在△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F.若BC=6,则DF的长为 .
【答案】3
13.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
【答案】20
考点3:特殊平行四边形的性质与判定
14.如图,在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( C )
A.4 B.6 C.8 D.10
15.如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为( D )
A.(2,2) B.(,2) C.(3,) D.(2,)
16.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,连接OE,则下列结论中不一定正确的是( C )
A.AB=AD B.OE=AB C.∠DOE=∠DEO D.∠EOD=∠EDO
17.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( C )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
18.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( C )
A.1 B. C.2 D.2
19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 ,使平行四边形ABCD是矩形.
【答案】∠ABC=90°(答案不唯一)
20.由沈康身教授所著、数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分),则图中AB的长应是 .
【答案】-1
21.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.在平面内有一个正方形,边长为2,中心为O,在正方形外有一点P,OP=2,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
【答案】2-≤d≤1
22.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.
求证:四边形AEDF是菱形.
证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠C,
AD∥BC,AB∥CD,
∵AF∥ED,∴四边形AEDF是平行四边形,
∵AD∥BC,∴∠DGC=∠ADE,
∵DG=DC,∴∠DGC=∠C,
∴∠BAD=∠ADE,∴AE=DE,
∴平行四边形AEDF是菱形.
23.如图,正方形ABCD的对角线相交于点O,E是正方形外部一点,以OE为边作正方形OEFG,OE与AB相交于点M,OG与BC相交于点N,若AB=6,OE=5,求四边形OMBN的面积 .
解:如图,过点O作OI⊥AB于点I,过点O作OH⊥BC于点H,
∴∠MIO=∠OIB=∠OHN=90°.∵在正方形ABCD中,∠ABC=90°,∠ABO=45°,∴四边形OIBH为矩形,∠BOI=45°=∠ABO. ∴BI=OI.∴四边形OIBH为正方形.∴OI=OH,∠IOH=90°.∴∠ION+∠HON=90°.∵∠EOG=90°,
∴∠MOI+∠ION=90°,∴∠MOI=∠NOH.
在△MOI与△NOH中,
∴△MOI≌△NOH(ASA).
∴四边形OMBN的面积等于正方形OIBH的面积.
由AB=6易得BI=3,∴正方形OIBH的面积为9,
即四边形OMBN的面积为9.
24.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
(1)求证:四边形EDFG是正方形;
(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.
(1)证明:连接CD,∵△ABC为等腰直角三角形,∠ACB=90°,
D是AB的中点,∴∠A=∠DCF=45°,AD=CD.
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,
∴△EDF为等腰直角三角形.∵O为EF的中点,GO=OD,∴GD⊥EF,
且GD=2OD=EF,∴四边形EDFG是正方形.
(2)解:过点D作DE′⊥AC于点E′.
∵△ABC为等腰直角三角形,∠ACB=90°,
AC=BC=4,∴DE′=BC=2,
AB==4.∵点E′为AC的中点,
∴2≤DE<2(点E与点E′重合时取等号),∴4≤S四边形EDFG=DE2<8,
∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.
