21.2.4 一元二次方程的根与系数的关系 课件(共25张PPT) 人教版数学九年级上册
文档属性
| 名称 | 21.2.4 一元二次方程的根与系数的关系 课件(共25张PPT) 人教版数学九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 18:34:57 | ||
图片预览







文档简介
(共25张PPT)
*21.2.4 一元二次方程的根与系数的关系
1.通过阅读课本学生可以掌握一元二次方程根与系数的关系,提高学生解决问题的能力.
2.通过自主探究经历探索一元二次方程根与系数的关系的过程,发展学生的逻辑推理和数学运算能力.
3.通过对根与系数之间关系的探究,体会事物之间的联系,发展学生归纳和推理论证的能力.
重点
难点
1.一元二次方程的一般形式是什么?
2.一元二次方程的求根公式是什么?
3.有实数根的条件是什么?
旧知回顾
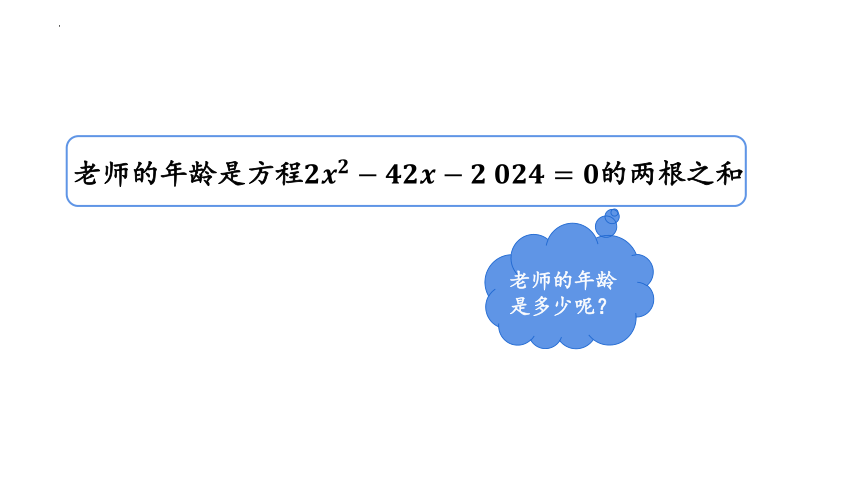
老师的年龄是方程的两根之和
老师的年龄是多少呢?
一天,小王去小明家玩,当时小明正为墨迹不小心污染了一道解一元二次方程的习题而愁眉不展,小王翻看了后面的答案后立马帮他补全了题目.这让解方程一向熟练的小明很惊讶,忙急着问小王有什么“秘法”.
小王的“秘法”
韦达,1540年生于法国的普瓦图,他把符号系统引入代数学,对数学的发展发挥了巨大的作用,人们为了纪念他在代数学上的功绩,称他为“代数学之父”.
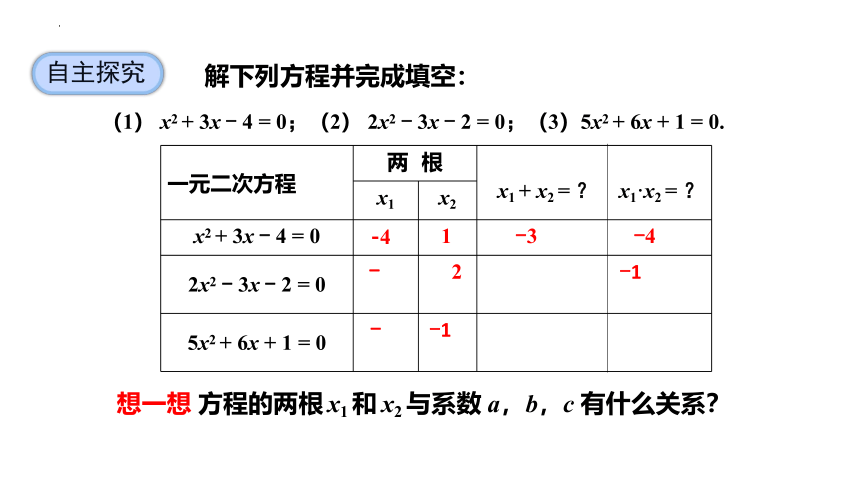
解下列方程并完成填空:
(1) x2 + 3x - 4 = 0;(2) 2x2 - 3x - 2 = 0;(3)5x2 + 6x + 1 = 0.
一元二次方程 两 根
x1 x2
x2 + 3x - 4 = 0 -4 1 -3 -4
2x2 - 3x - 2 = 0 - 2 -1
5x2 + 6x + 1 = 0 - -1
x1 + x2 = ?
x1·x2 = ?
想一想 方程的两根 x1 和 x2 与系数 a,b,c 有什么关系?
自主探究
2.完成表格后请同学们思考以下问题:
①针对表格中第一个方程.
猜想:方程可通过因式分解化为
,与的值与之间的关系.
②针对表格中第二、三个方程.
猜想:方程的两根的和、积与之间的关系.
③你能证明一下上述两个猜想吗?
)
)
(第一个猜想证明方法:把方程化为一般形式与对比;第二个猜想证明方法:通过求根公式.方法不唯一)
小组讨论
已知一元二次方程的两个根.
(1)利用根与系数的关系,求方程两根的平方和;
(2)求方程两根的倒数和.
小组展示
我提问
我回答
我补充
我质疑
提疑惑:你有什么疑惑?
越展越优秀
教师讲评
知识点1:一元二次方程的根与系数的关系(重点)
注意它的使用条件为a≠0, Δ≥0.
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
如果一元二次方程 的两个实数根是x ,x , 那么
教师讲评
知识点2:一元二次方程的根与系数的关系的应用(难点)
(1)验根.不解方程,利用根与系数的关系可以检验两个数是不是一元二次方程的两个根;
(2)已知方程的一个根,求方程的另一个根及未知系数;
(3)不解方程,可以利用根与系数的关系求关于x 、x 的对称式的值.此时常常涉及代数式的一些重要变形;
教师讲评
教师讲评
⑦;
⑧
⑨;
教师讲评
(4)已知方程的两根,求作一个一元二次方程.以两个数x ,x 为根的一元二次方程是x - (x +x )x+x x =0 .
(5)已知一元二次方程的两根满足某种关系,确定方程中字母系数的值或取值范围.
教师讲评
(6)利用一元二次方程根与系数的关系可以进一步讨论根的符号.设一元二次方程ax +bx+c=0(a≠0)的两根为x 、x ,则
①当Δ≥0且x x >0时,两根同号.
当Δ≥0且x x >0,x +x >0时,两根同为正数;
当Δ≥0且x x >0,x +x <0时,两根同为负数.
②当Δ>0且x x <0时,两根异号.
当Δ>0且x x <0,x +x >0时,两根异号且正根的绝对值较大;
当Δ>0且x x <0,x +x <0时,两根异号且负根的绝对值较大.
教师讲评
注 :(1)利用根与系数的关系求出一元二次方程中的待定系数后, 一定要验证方程的Δ.一些考试中,往往利用这一点设置陷阱;
(2)若有理系数一元二次方程有一根为a+,则必有一根为a- (a,b为有理数).
【题型一】根与系数的关系
例1:已知一元二次方程2x -3x=10 的两根分别为x1,x2, 则x +x2= ______.
变式:已知关于x的一元二次方程若方程的两根之积等于0,则
点拨:方程化为一般形式为 故
点拨:由题意,得
解得 .
【题型二】已知方程及方程的一个根
例2: 若 是关于x的方程 的一个根,则方程的另一个根是________ .
变式:若关于x的一元二次方程 的一个实数根为2,则另一实数根和m的值分别为 ( )
D.4,8
1
点拨:设方程的另一个根为x ,由题意,得解得 故答案为1.
A
点拨:设方程的另一实数根为x .由题意,得 解得故选A.
【题型三】求与根有关的代数式的值
例3:已知方程 的两根分别为m,n,则
点拨:∵方程的两根分别为m,n,
由根与系数的关系,得
-1
【题型三】求与根有关的代数式的值
变式:已知a,b是一元二次方程 的两个根,那么 的值为 ______.
3
点拨:方程化为一般形式为
由根与系数的关系,得
∴ab +a b=ab(a+b)=3.
【题型四】给出两根满足的条件,求参数的值
例4:已知一元二次方程x -(2m-1)x+m =0的两根分别为x1,x2,且满足x +x +4=x x ,则m的值为 .
点拨:由根与系数的关系,得x +x =2m- 1,x x =m ,
∴2m- 1+4=m ,解得m =3,m =- 1.
∵一元二次方程x -(2m-1)x+m =0有两个实数根,
∴Δ=(2m-1) -4m =-4m+1≥0,解得m≤ ,∴m=-1.
- 1
变式 若关于的一元二次方程的两个实数根分别为,且,则的值为__________.
1
点拨:由根与系数的关系,得x +x =2,
∴x +2x =x +x +x =2+x =5,
∴x =3.把x =3代入x -2x-3m=0,解得m=1.
今天我们学习了哪些重要的知识呢?
1.根与系数的关系;
2.与方程根有关的常见变形.
【教材习题】完成课本16页练习.
【实践性作业】请你制作一个矩形,要求:矩形的长、宽分别为方程2x2-8x+7=0的两根之和、两根之积.
*21.2.4 一元二次方程的根与系数的关系
1.通过阅读课本学生可以掌握一元二次方程根与系数的关系,提高学生解决问题的能力.
2.通过自主探究经历探索一元二次方程根与系数的关系的过程,发展学生的逻辑推理和数学运算能力.
3.通过对根与系数之间关系的探究,体会事物之间的联系,发展学生归纳和推理论证的能力.
重点
难点
1.一元二次方程的一般形式是什么?
2.一元二次方程的求根公式是什么?
3.有实数根的条件是什么?
旧知回顾
老师的年龄是方程的两根之和
老师的年龄是多少呢?
一天,小王去小明家玩,当时小明正为墨迹不小心污染了一道解一元二次方程的习题而愁眉不展,小王翻看了后面的答案后立马帮他补全了题目.这让解方程一向熟练的小明很惊讶,忙急着问小王有什么“秘法”.
小王的“秘法”
韦达,1540年生于法国的普瓦图,他把符号系统引入代数学,对数学的发展发挥了巨大的作用,人们为了纪念他在代数学上的功绩,称他为“代数学之父”.
解下列方程并完成填空:
(1) x2 + 3x - 4 = 0;(2) 2x2 - 3x - 2 = 0;(3)5x2 + 6x + 1 = 0.
一元二次方程 两 根
x1 x2
x2 + 3x - 4 = 0 -4 1 -3 -4
2x2 - 3x - 2 = 0 - 2 -1
5x2 + 6x + 1 = 0 - -1
x1 + x2 = ?
x1·x2 = ?
想一想 方程的两根 x1 和 x2 与系数 a,b,c 有什么关系?
自主探究
2.完成表格后请同学们思考以下问题:
①针对表格中第一个方程.
猜想:方程可通过因式分解化为
,与的值与之间的关系.
②针对表格中第二、三个方程.
猜想:方程的两根的和、积与之间的关系.
③你能证明一下上述两个猜想吗?
)
)
(第一个猜想证明方法:把方程化为一般形式与对比;第二个猜想证明方法:通过求根公式.方法不唯一)
小组讨论
已知一元二次方程的两个根.
(1)利用根与系数的关系,求方程两根的平方和;
(2)求方程两根的倒数和.
小组展示
我提问
我回答
我补充
我质疑
提疑惑:你有什么疑惑?
越展越优秀
教师讲评
知识点1:一元二次方程的根与系数的关系(重点)
注意它的使用条件为a≠0, Δ≥0.
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
如果一元二次方程 的两个实数根是x ,x , 那么
教师讲评
知识点2:一元二次方程的根与系数的关系的应用(难点)
(1)验根.不解方程,利用根与系数的关系可以检验两个数是不是一元二次方程的两个根;
(2)已知方程的一个根,求方程的另一个根及未知系数;
(3)不解方程,可以利用根与系数的关系求关于x 、x 的对称式的值.此时常常涉及代数式的一些重要变形;
教师讲评
教师讲评
⑦;
⑧
⑨;
教师讲评
(4)已知方程的两根,求作一个一元二次方程.以两个数x ,x 为根的一元二次方程是x - (x +x )x+x x =0 .
(5)已知一元二次方程的两根满足某种关系,确定方程中字母系数的值或取值范围.
教师讲评
(6)利用一元二次方程根与系数的关系可以进一步讨论根的符号.设一元二次方程ax +bx+c=0(a≠0)的两根为x 、x ,则
①当Δ≥0且x x >0时,两根同号.
当Δ≥0且x x >0,x +x >0时,两根同为正数;
当Δ≥0且x x >0,x +x <0时,两根同为负数.
②当Δ>0且x x <0时,两根异号.
当Δ>0且x x <0,x +x >0时,两根异号且正根的绝对值较大;
当Δ>0且x x <0,x +x <0时,两根异号且负根的绝对值较大.
教师讲评
注 :(1)利用根与系数的关系求出一元二次方程中的待定系数后, 一定要验证方程的Δ.一些考试中,往往利用这一点设置陷阱;
(2)若有理系数一元二次方程有一根为a+,则必有一根为a- (a,b为有理数).
【题型一】根与系数的关系
例1:已知一元二次方程2x -3x=10 的两根分别为x1,x2, 则x +x2= ______.
变式:已知关于x的一元二次方程若方程的两根之积等于0,则
点拨:方程化为一般形式为 故
点拨:由题意,得
解得 .
【题型二】已知方程及方程的一个根
例2: 若 是关于x的方程 的一个根,则方程的另一个根是________ .
变式:若关于x的一元二次方程 的一个实数根为2,则另一实数根和m的值分别为 ( )
D.4,8
1
点拨:设方程的另一个根为x ,由题意,得解得 故答案为1.
A
点拨:设方程的另一实数根为x .由题意,得 解得故选A.
【题型三】求与根有关的代数式的值
例3:已知方程 的两根分别为m,n,则
点拨:∵方程的两根分别为m,n,
由根与系数的关系,得
-1
【题型三】求与根有关的代数式的值
变式:已知a,b是一元二次方程 的两个根,那么 的值为 ______.
3
点拨:方程化为一般形式为
由根与系数的关系,得
∴ab +a b=ab(a+b)=3.
【题型四】给出两根满足的条件,求参数的值
例4:已知一元二次方程x -(2m-1)x+m =0的两根分别为x1,x2,且满足x +x +4=x x ,则m的值为 .
点拨:由根与系数的关系,得x +x =2m- 1,x x =m ,
∴2m- 1+4=m ,解得m =3,m =- 1.
∵一元二次方程x -(2m-1)x+m =0有两个实数根,
∴Δ=(2m-1) -4m =-4m+1≥0,解得m≤ ,∴m=-1.
- 1
变式 若关于的一元二次方程的两个实数根分别为,且,则的值为__________.
1
点拨:由根与系数的关系,得x +x =2,
∴x +2x =x +x +x =2+x =5,
∴x =3.把x =3代入x -2x-3m=0,解得m=1.
今天我们学习了哪些重要的知识呢?
1.根与系数的关系;
2.与方程根有关的常见变形.
【教材习题】完成课本16页练习.
【实践性作业】请你制作一个矩形,要求:矩形的长、宽分别为方程2x2-8x+7=0的两根之和、两根之积.
同课章节目录
