人教版数学八年级下册18.2.1 矩形 课件(18张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.1 矩形 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 560.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
18.2.1 矩形
请在此输入您的副标题
温故知新
1.矩形的定义
有一个角是直角的平行四边形是矩形
2.矩形的性质
四个内角都是直角
对边平行且相等
对角线相等且互相平分
边 角 对角线
(矩形是特殊的平行四边形,所以矩形既具有
平行四边形的共性,又具有自身的特殊性)
(矩形的角、对角线具有特性)
矩形性质
1、类比平行四边形的学习你认为这节课我们会从哪几个方面继续来研究矩形?
定义——性质——判定——运用
2、你知道如何判定一个平行四边形是矩形吗?
新知探究
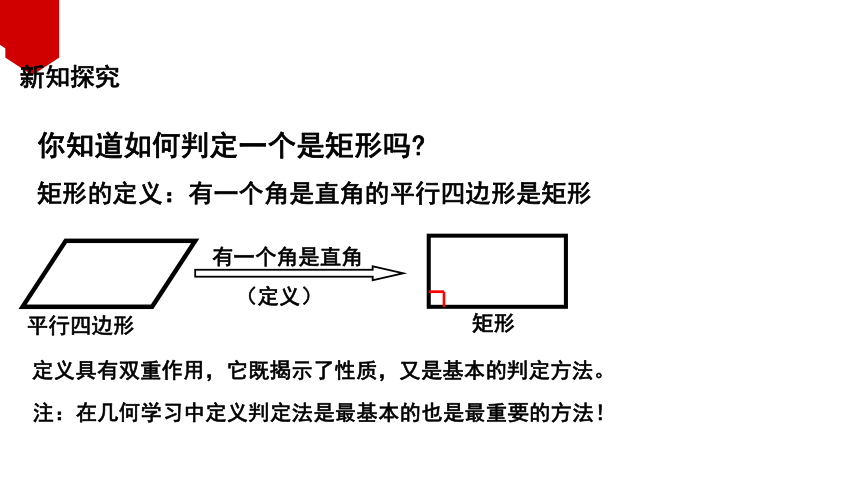
你知道如何判定一个是矩形吗
有一个角是直角
定义具有双重作用,它既揭示了性质,又是基本的判定方法。
(定义)
矩形的定义:有一个角是直角的平行四边形是矩形
注:在几何学习中定义判定法是最基本的也是最重要的方法!
平行四边形
矩形
新知探究
定义判定:有一个角是直角的平行四边形是矩形
用定义判定矩形,需要具备几个条件?
有一个角是直角
平行四边形
如何用几何语言来表述呢?
矩形
新知探究
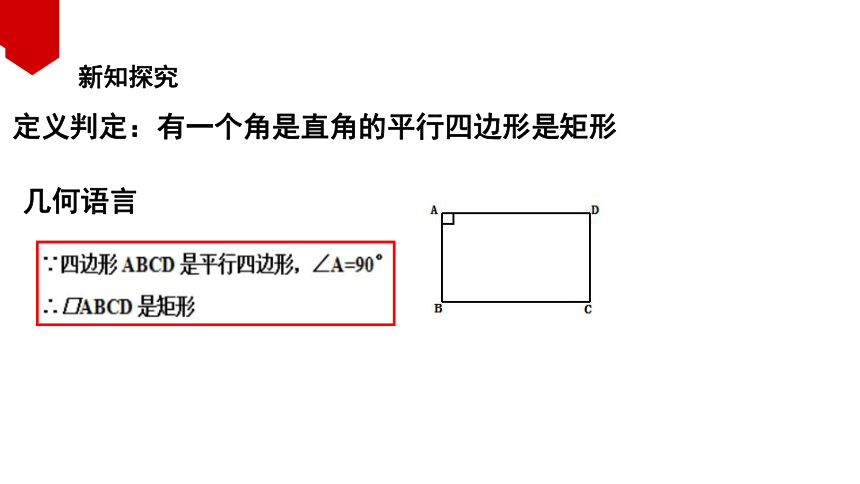
定义判定:有一个角是直角的平行四边形是矩形
几何语言
新知探究
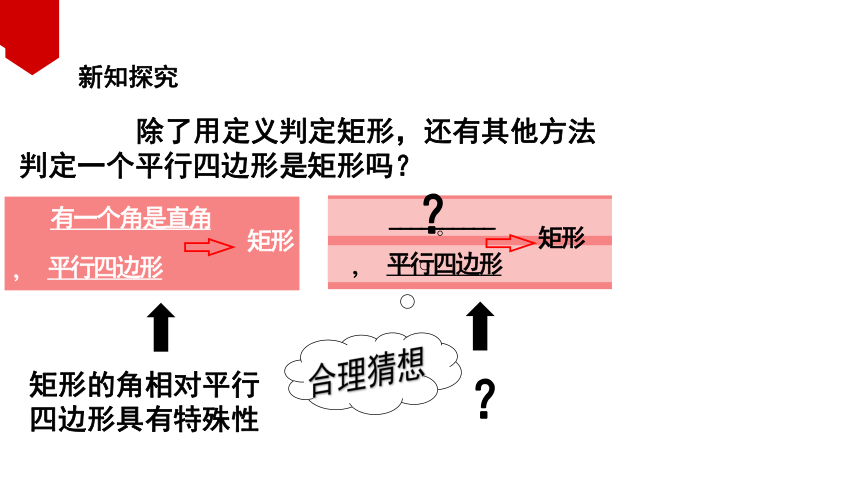
除了用定义判定矩形,还有其他方法判定一个平行四边形是矩形吗?
有一个角是直角
平行四边形
矩形
__________
平行四边形
矩形
矩形的角相对平行四边形具有特殊性
?
合理猜想
新知探究
?
除了角以外,矩形对角线也具有特殊性(矩形的特性)
猜想:对角线相等的平行四边形是矩形
除了用定义判定矩形,你还有其他方法判定一个平行四边形是矩形吗?
对角线相等
平行四边形
矩形
?
合理猜想
新知探究
操作验证——感性直观
猜想:对角线相等的平行四边形是矩形
怎样验证猜想?
推理验证——理性严谨
注:探究的一般步骤:猜想——验证——结论
(推理证明)
新知探究
条件
条件
结论
如图,□ABCD的两条对角线交于点O,AC=DB
□ABCD是矩形.
我们已有证明的依据: .
要证明矩形,目前我们还缺少: .
有一个角是直角的平行四边形是矩形
一个直角
如何证明?我们先来思考2个问题
猜想:对角线相等的平行四边形是矩形
求证:
已知:
证明:
证明命题的步骤?
这个命题的条件和结论是什么?
新知探究
新知探究
已知:如图,□ABCD的两条对角线交于点O,AC=DB
求证:□ABCD是矩形.
猜想正确!
定义判定
判定定理1:
对角线相等的平行四边形是矩形
判定定理1:对角线相等的平行四边形是矩形
这个条件不能弱化
对角线相等的四边形是矩形吗?
B
C
A
D
(不一定)
能否将条件弱化?
条件弱化
四边形
新知探究
思考1:除了对角线相等,矩形还有什么特性?
矩形的四个角都是直角(特性)
思考2:一个四边形至少有几个角是直角时,成为矩形?
新知探究
①只有一个角是直角的四边形是矩形吗?
②有两个角是直角的四边形是矩形吗?
③有三个角是直角的四边形是矩形吗?
矩形
猜想:有三个角是直角的四边形是矩形
思考2:一个四边形至少有几个角是直角时,成为矩形?
你能得到什么猜想?
直角梯形
新知探究
新知探究
猜想:有三个角是直角的四边形是矩形
已知:如图,四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形.
证明:
∵∠A=∠B=∠C=90°
∴∠A+∠B=180°,∠B+∠C=180°
∴ AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
又∵∠A=90°
∴四边形ABCD是矩形
判定定理2:有三个角是直角的四边形是矩形
你会证明自己的猜想吗
定义判定
判定定理2:有三个角是直角的四边形是矩形
思考:为什么判断一个四边形是矩
形,不用找四个直角,只要
找三个直角就可以了呢?
注:体现数学的精炼和简洁美!
新知探究
四边形
课堂小结
归纳:如何判定一个四边形是矩形?
平行四边形
矩形
一个直角
对角线相等
三个直角
注:以后涉及矩形的判定,我们可以用这一思路来解决。
平行四边形的判定方法
矩形的判定方法
祝同学们天天进步!
18.2.1 矩形
请在此输入您的副标题
温故知新
1.矩形的定义
有一个角是直角的平行四边形是矩形
2.矩形的性质
四个内角都是直角
对边平行且相等
对角线相等且互相平分
边 角 对角线
(矩形是特殊的平行四边形,所以矩形既具有
平行四边形的共性,又具有自身的特殊性)
(矩形的角、对角线具有特性)
矩形性质
1、类比平行四边形的学习你认为这节课我们会从哪几个方面继续来研究矩形?
定义——性质——判定——运用
2、你知道如何判定一个平行四边形是矩形吗?
新知探究
你知道如何判定一个是矩形吗
有一个角是直角
定义具有双重作用,它既揭示了性质,又是基本的判定方法。
(定义)
矩形的定义:有一个角是直角的平行四边形是矩形
注:在几何学习中定义判定法是最基本的也是最重要的方法!
平行四边形
矩形
新知探究
定义判定:有一个角是直角的平行四边形是矩形
用定义判定矩形,需要具备几个条件?
有一个角是直角
平行四边形
如何用几何语言来表述呢?
矩形
新知探究
定义判定:有一个角是直角的平行四边形是矩形
几何语言
新知探究
除了用定义判定矩形,还有其他方法判定一个平行四边形是矩形吗?
有一个角是直角
平行四边形
矩形
__________
平行四边形
矩形
矩形的角相对平行四边形具有特殊性
?
合理猜想
新知探究
?
除了角以外,矩形对角线也具有特殊性(矩形的特性)
猜想:对角线相等的平行四边形是矩形
除了用定义判定矩形,你还有其他方法判定一个平行四边形是矩形吗?
对角线相等
平行四边形
矩形
?
合理猜想
新知探究
操作验证——感性直观
猜想:对角线相等的平行四边形是矩形
怎样验证猜想?
推理验证——理性严谨
注:探究的一般步骤:猜想——验证——结论
(推理证明)
新知探究
条件
条件
结论
如图,□ABCD的两条对角线交于点O,AC=DB
□ABCD是矩形.
我们已有证明的依据: .
要证明矩形,目前我们还缺少: .
有一个角是直角的平行四边形是矩形
一个直角
如何证明?我们先来思考2个问题
猜想:对角线相等的平行四边形是矩形
求证:
已知:
证明:
证明命题的步骤?
这个命题的条件和结论是什么?
新知探究
新知探究
已知:如图,□ABCD的两条对角线交于点O,AC=DB
求证:□ABCD是矩形.
猜想正确!
定义判定
判定定理1:
对角线相等的平行四边形是矩形
判定定理1:对角线相等的平行四边形是矩形
这个条件不能弱化
对角线相等的四边形是矩形吗?
B
C
A
D
(不一定)
能否将条件弱化?
条件弱化
四边形
新知探究
思考1:除了对角线相等,矩形还有什么特性?
矩形的四个角都是直角(特性)
思考2:一个四边形至少有几个角是直角时,成为矩形?
新知探究
①只有一个角是直角的四边形是矩形吗?
②有两个角是直角的四边形是矩形吗?
③有三个角是直角的四边形是矩形吗?
矩形
猜想:有三个角是直角的四边形是矩形
思考2:一个四边形至少有几个角是直角时,成为矩形?
你能得到什么猜想?
直角梯形
新知探究
新知探究
猜想:有三个角是直角的四边形是矩形
已知:如图,四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形.
证明:
∵∠A=∠B=∠C=90°
∴∠A+∠B=180°,∠B+∠C=180°
∴ AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
又∵∠A=90°
∴四边形ABCD是矩形
判定定理2:有三个角是直角的四边形是矩形
你会证明自己的猜想吗
定义判定
判定定理2:有三个角是直角的四边形是矩形
思考:为什么判断一个四边形是矩
形,不用找四个直角,只要
找三个直角就可以了呢?
注:体现数学的精炼和简洁美!
新知探究
四边形
课堂小结
归纳:如何判定一个四边形是矩形?
平行四边形
矩形
一个直角
对角线相等
三个直角
注:以后涉及矩形的判定,我们可以用这一思路来解决。
平行四边形的判定方法
矩形的判定方法
祝同学们天天进步!
