人教版数学八年级下册18.2.2 菱形 课件(15张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.2 菱形 课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 939.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 18:48:30 | ||
图片预览





文档简介
(共15张PPT)
菱形
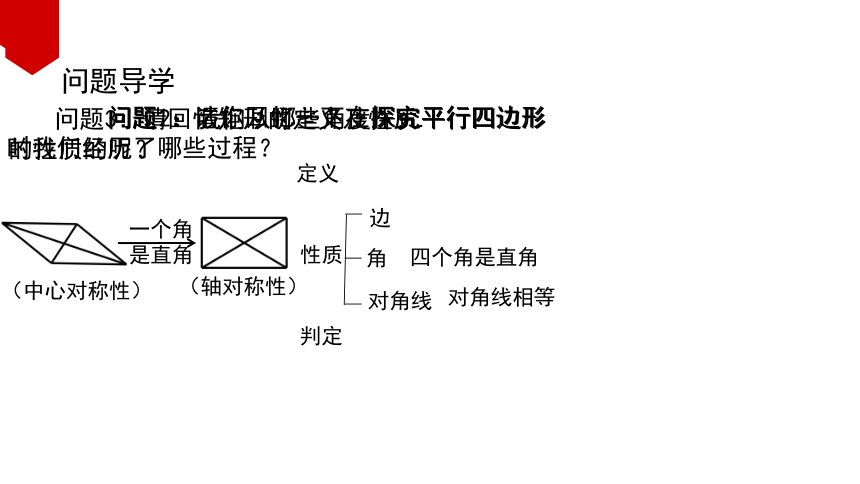
问题1:请你回忆一下在探究平行四边形
时我们经历了哪些过程?
问题导学
定义
性质
判定
(中心对称性)
问题2:我们从哪些角度探究平行四边形
的性质的呢?
边
角
问题3:请回忆矩形的定义及性质.
四个角是直角
对角线相等
(轴对称性)
一个角
是直角
对角线
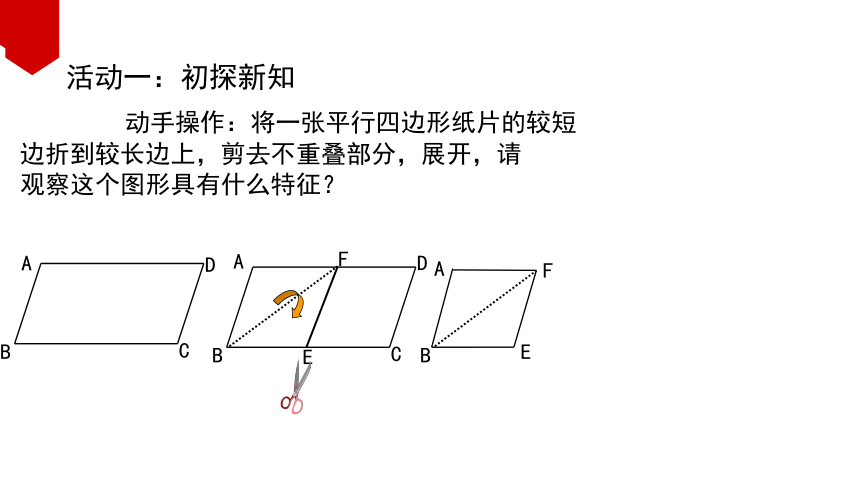
活动一:初探新知
动手操作:将一张平行四边形纸片的较短
边折到较长边上,剪去不重叠部分,展开,请
观察这个图形具有什么特征?
A
B
C
D
A
B
C
D
E
F
A
B
E
F
活动一:初探新知
动手操作:将一张平行四边形纸片的较短
边折到较长边上,剪去不重叠部分,展开,请
观察这个图形具有什么特征?
A
B
F
1
2
3
4
由折叠得:AB=BE AF=EF
折痕BF平分∠ABE与∠AFE
E
由 ABCD得:AF∥BE
可以得到:∠2=∠3
分析:
又∵∠1=∠2 得∠1=∠3
可以证明AB=AF
可证明四边形ABEF是平行四边形
活动一:初探新知
类比矩形的定义方式,你能给出菱形的定义吗?
菱形的定义:有一组邻边相等的平行四边形
叫做菱形.
一组邻边相等
生活中的“菱形”
活动二:再探新知
问题:与矩形一样,做为特殊的平行
四边形,菱形肯定也具有平行四边形的一
切性质,它还有哪些特殊性呢?你准备从
哪些角度探究它的特殊性呢?
对角线
角
边
一组邻边相等
你能用已学知识证明你的发现吗?
请同学们写出你们的证明过程.
定义: 的 叫做菱形.
平行四边形
一组邻边相等
AB=CD AD=BC
AB=BC
OB=OD
AB=AD
活动二:再探新知
AB=BC=CD=AD
AC⊥BD
AC平分∠BAD
A
B
C
D
O
边:四条边都相等
对角线:两条对角线互相垂
直,每条对角线平分一组对角
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
几何语言:
∵四边形ABCD为菱形
∴ AB=BC=CD=AD AC⊥BD
AC平分∠BAD、∠BCD
BD平分∠ABC、∠ADC
活动二:再探新知
A
B
C
D
O
在菱形ABCD中,令AC= ,BD= ,你能求
出图形中的哪些相关量?
解: ∵四边形ABCD是菱形
∴ AO= ,BO= ,AC⊥BD,
在Rt△AOB中, ∠AOB=90°
菱形ABCD的周长为20
AB=BC=CD=AD
可证明: △ABC≌ △ADC
法二:△AOB≌△AOD ≌ △COB≌ △COD
6
n
m
8
菱形ABCD的周长为
4
3
E
活动三:应用新知
B
C
O
A
D
活动四 联系生活 应用新知
如图,小明妈妈准备在网上买一个可伸缩挂衣钩,是由
三个全等的菱形构成.小明妈妈选择的挂衣钩每个菱形边
长为13cm,妈妈把菱形挂衣钩的长度拉到72cm,你能帮
妈妈算出此时菱形挂衣钩的高吗?
A
B
C
D
O
解:如图,连接AC、BD,AC与BD相交于点O,BD=24cm
∵四边形ABCD是菱形
∴∠AOB=90°,BO
∴
∴AC=2AO=10 cm
即菱形挂衣钩的高为10cm
24cm
13cm
生活中的“菱形”
是什么?
怎么学?
转化
操作、观察、
猜想、证明
为什么?
类比
解决问题
菱形的定
义和性质
归纳小结
通过今天的学习,同学们有
哪些收获呢?
定义
性质
判定
归纳小结
一个角是直角
一组邻边
相等
同学们,再见!
01
菱形
问题1:请你回忆一下在探究平行四边形
时我们经历了哪些过程?
问题导学
定义
性质
判定
(中心对称性)
问题2:我们从哪些角度探究平行四边形
的性质的呢?
边
角
问题3:请回忆矩形的定义及性质.
四个角是直角
对角线相等
(轴对称性)
一个角
是直角
对角线
活动一:初探新知
动手操作:将一张平行四边形纸片的较短
边折到较长边上,剪去不重叠部分,展开,请
观察这个图形具有什么特征?
A
B
C
D
A
B
C
D
E
F
A
B
E
F
活动一:初探新知
动手操作:将一张平行四边形纸片的较短
边折到较长边上,剪去不重叠部分,展开,请
观察这个图形具有什么特征?
A
B
F
1
2
3
4
由折叠得:AB=BE AF=EF
折痕BF平分∠ABE与∠AFE
E
由 ABCD得:AF∥BE
可以得到:∠2=∠3
分析:
又∵∠1=∠2 得∠1=∠3
可以证明AB=AF
可证明四边形ABEF是平行四边形
活动一:初探新知
类比矩形的定义方式,你能给出菱形的定义吗?
菱形的定义:有一组邻边相等的平行四边形
叫做菱形.
一组邻边相等
生活中的“菱形”
活动二:再探新知
问题:与矩形一样,做为特殊的平行
四边形,菱形肯定也具有平行四边形的一
切性质,它还有哪些特殊性呢?你准备从
哪些角度探究它的特殊性呢?
对角线
角
边
一组邻边相等
你能用已学知识证明你的发现吗?
请同学们写出你们的证明过程.
定义: 的 叫做菱形.
平行四边形
一组邻边相等
AB=CD AD=BC
AB=BC
OB=OD
AB=AD
活动二:再探新知
AB=BC=CD=AD
AC⊥BD
AC平分∠BAD
A
B
C
D
O
边:四条边都相等
对角线:两条对角线互相垂
直,每条对角线平分一组对角
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
几何语言:
∵四边形ABCD为菱形
∴ AB=BC=CD=AD AC⊥BD
AC平分∠BAD、∠BCD
BD平分∠ABC、∠ADC
活动二:再探新知
A
B
C
D
O
在菱形ABCD中,令AC= ,BD= ,你能求
出图形中的哪些相关量?
解: ∵四边形ABCD是菱形
∴ AO= ,BO= ,AC⊥BD,
在Rt△AOB中, ∠AOB=90°
菱形ABCD的周长为20
AB=BC=CD=AD
可证明: △ABC≌ △ADC
法二:△AOB≌△AOD ≌ △COB≌ △COD
6
n
m
8
菱形ABCD的周长为
4
3
E
活动三:应用新知
B
C
O
A
D
活动四 联系生活 应用新知
如图,小明妈妈准备在网上买一个可伸缩挂衣钩,是由
三个全等的菱形构成.小明妈妈选择的挂衣钩每个菱形边
长为13cm,妈妈把菱形挂衣钩的长度拉到72cm,你能帮
妈妈算出此时菱形挂衣钩的高吗?
A
B
C
D
O
解:如图,连接AC、BD,AC与BD相交于点O,BD=24cm
∵四边形ABCD是菱形
∴∠AOB=90°,BO
∴
∴AC=2AO=10 cm
即菱形挂衣钩的高为10cm
24cm
13cm
生活中的“菱形”
是什么?
怎么学?
转化
操作、观察、
猜想、证明
为什么?
类比
解决问题
菱形的定
义和性质
归纳小结
通过今天的学习,同学们有
哪些收获呢?
定义
性质
判定
归纳小结
一个角是直角
一组邻边
相等
同学们,再见!
01
