人教版数学八年级下册18.2.2 菱形的性质 课件(17张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.2 菱形的性质 课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 18:49:18 | ||
图片预览




文档简介
(共17张PPT)
18.2.2菱形(菱形的性质)
请在此输入您的副标题
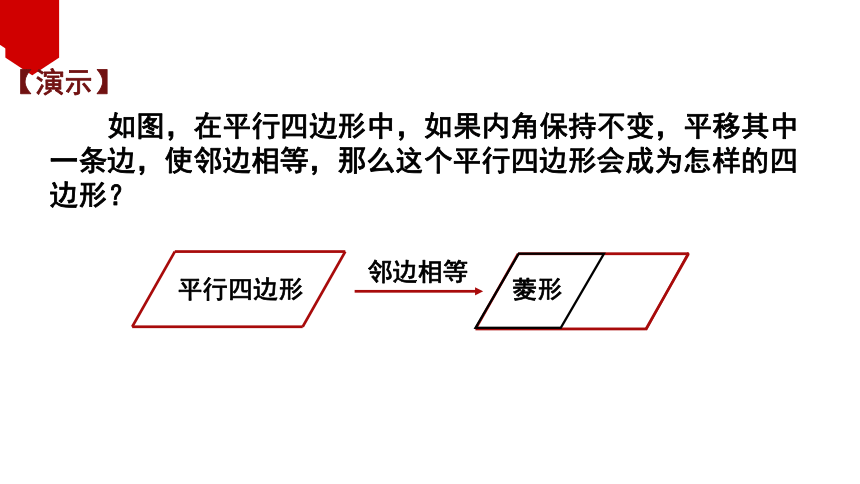
平行四边形
邻边相等
菱形
如图,在平行四边形中,如果内角保持不变,平移其中一条边,使邻边相等,那么这个平行四边形会成为怎样的四边形?
【演示】
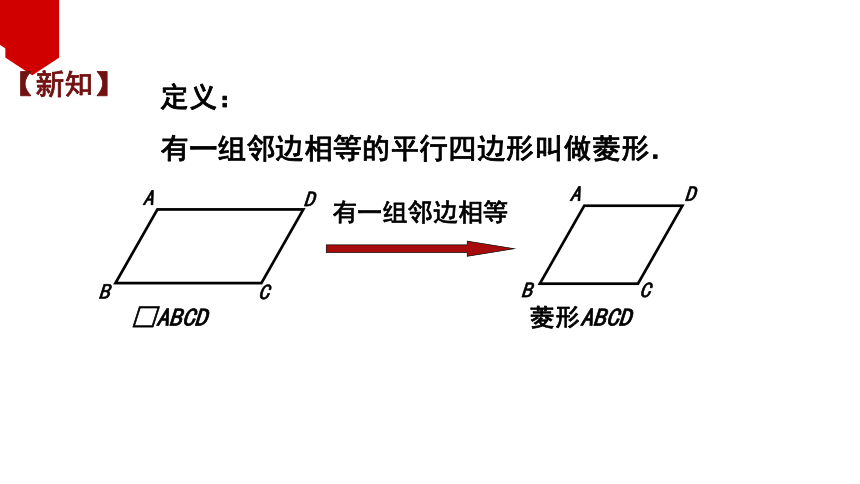
有一组邻边相等
定义:
有一组邻边相等的平行四边形叫做菱形.
A
D
B
C
A
D
B
C
菱形ABCD
□ABCD
【新知】
你能举出生活中具有菱形形象的实际例子吗?
【数学与生活】
平行四边形
菱形
请在合适的位置填空:平行四边形、矩形、菱形.
【联系与区别】
矩形
平行四边形
菱形
菱形是特殊的平行四边形,那么它具有平行四边形的一切性质:
对边平行且相等
对角相等
对角线互相平分
【温故知新】
边
角
对角线
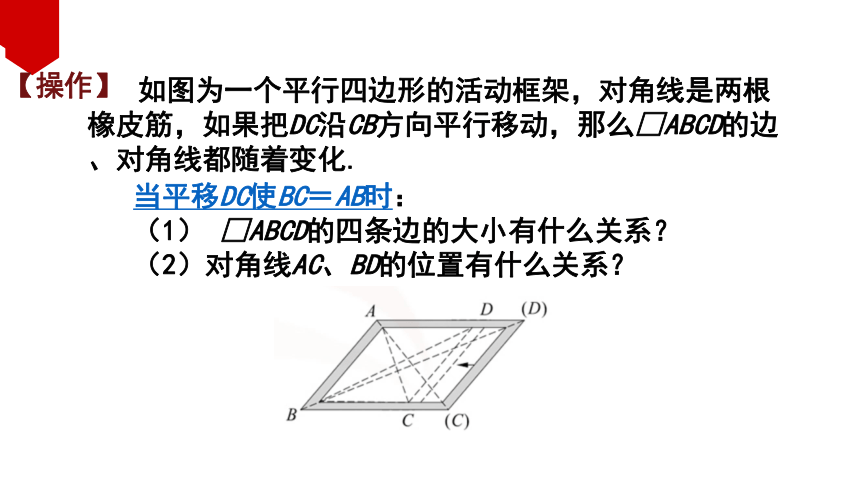
如图为一个平行四边形的活动框架,对角线是两根橡皮筋,如果把DC沿CB方向平行移动,那么□ABCD的边、对角线都随着变化.
当平移DC使BC=AB时:
(1) □ABCD的四条边的大小有什么关系?
(2)对角线AC、BD的位置有什么关系?
【操作】
性质定理1:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
A
D
B
C
【新知】
几何语言:
∵菱形ABCD
∴AB=BC=CD=DA
已知:如图,菱形ABCD的对角线AC和BD
相交于点O.
求证:(1)AC⊥BD,
(2)AC平分∠BAD、 ∠BCD,
BD平分∠ABC、 ∠ADC.
性质定理2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
O
A
D
B
C
几何语言:
∵菱形ABCD
∴ AC⊥BD,
AC平分∠BAD、 ∠BCD
BD平分∠ABC、 ∠ADC
轴对称
边 角 对角线 对称性
平行四边形
菱形
对边平行且相等
对角相等
对角线互相平分
对边平行四边相等
对角相等
对角线互相平分且垂直,平分一组对角
轴对称
【联系与区别】
菱形
性质
对称性
定义
有一组邻边相等的平行四边形
对角线
角
边
对边平行、四边相等
对角相等
对角线互相平分且垂直,
每一条对角线平分一组对角
轴对称
【归纳】
例 如图,菱形ABCD中,对角线AC、BD
相交于点O,E、F、G、H分别是菱形ABCD
各边的中点,
求证:OE=OF=OG=OH
菱形面积=底×高=对角线乘积的一半
S菱形ABCD
【探究】
(1)在上述问题中若去掉四个中点、四条中线,如图所示,则菱形被分成几个怎样的三角形?
=4S△AOB
(2)如图,若连接EF、FG、GH、HE,则四边形EFGH是________.为什么?
练习 如图,菱形花坛ABCD的边长为20m ,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
A
B
C
D
O
【总结】
菱形
性质
对称性
定义
判定
有一组邻边相等的平行四边形
对角线
角
边
对边平行、四边相等
对角相等
对角线互相平分且垂直,
每一条对角线平分一组对角
轴对称
……
平行四边形
特殊化
一般到特殊
类比思想
分类思想
转化思想
操作
猜想
证明
【拓展】
如图,矩形OABC在平面直角坐标系中,AC=5,OA=3,把矩形OABC沿直线DE对折使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,点M在y轴上,点N在坐标平面内,若四边形MFDN
是菱形,则菱形MFDN的面积
是_______.
M
N
18.2.2菱形(菱形的性质)
请在此输入您的副标题
平行四边形
邻边相等
菱形
如图,在平行四边形中,如果内角保持不变,平移其中一条边,使邻边相等,那么这个平行四边形会成为怎样的四边形?
【演示】
有一组邻边相等
定义:
有一组邻边相等的平行四边形叫做菱形.
A
D
B
C
A
D
B
C
菱形ABCD
□ABCD
【新知】
你能举出生活中具有菱形形象的实际例子吗?
【数学与生活】
平行四边形
菱形
请在合适的位置填空:平行四边形、矩形、菱形.
【联系与区别】
矩形
平行四边形
菱形
菱形是特殊的平行四边形,那么它具有平行四边形的一切性质:
对边平行且相等
对角相等
对角线互相平分
【温故知新】
边
角
对角线
如图为一个平行四边形的活动框架,对角线是两根橡皮筋,如果把DC沿CB方向平行移动,那么□ABCD的边、对角线都随着变化.
当平移DC使BC=AB时:
(1) □ABCD的四条边的大小有什么关系?
(2)对角线AC、BD的位置有什么关系?
【操作】
性质定理1:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
A
D
B
C
【新知】
几何语言:
∵菱形ABCD
∴AB=BC=CD=DA
已知:如图,菱形ABCD的对角线AC和BD
相交于点O.
求证:(1)AC⊥BD,
(2)AC平分∠BAD、 ∠BCD,
BD平分∠ABC、 ∠ADC.
性质定理2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
O
A
D
B
C
几何语言:
∵菱形ABCD
∴ AC⊥BD,
AC平分∠BAD、 ∠BCD
BD平分∠ABC、 ∠ADC
轴对称
边 角 对角线 对称性
平行四边形
菱形
对边平行且相等
对角相等
对角线互相平分
对边平行四边相等
对角相等
对角线互相平分且垂直,平分一组对角
轴对称
【联系与区别】
菱形
性质
对称性
定义
有一组邻边相等的平行四边形
对角线
角
边
对边平行、四边相等
对角相等
对角线互相平分且垂直,
每一条对角线平分一组对角
轴对称
【归纳】
例 如图,菱形ABCD中,对角线AC、BD
相交于点O,E、F、G、H分别是菱形ABCD
各边的中点,
求证:OE=OF=OG=OH
菱形面积=底×高=对角线乘积的一半
S菱形ABCD
【探究】
(1)在上述问题中若去掉四个中点、四条中线,如图所示,则菱形被分成几个怎样的三角形?
=4S△AOB
(2)如图,若连接EF、FG、GH、HE,则四边形EFGH是________.为什么?
练习 如图,菱形花坛ABCD的边长为20m ,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
A
B
C
D
O
【总结】
菱形
性质
对称性
定义
判定
有一组邻边相等的平行四边形
对角线
角
边
对边平行、四边相等
对角相等
对角线互相平分且垂直,
每一条对角线平分一组对角
轴对称
……
平行四边形
特殊化
一般到特殊
类比思想
分类思想
转化思想
操作
猜想
证明
【拓展】
如图,矩形OABC在平面直角坐标系中,AC=5,OA=3,把矩形OABC沿直线DE对折使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,点M在y轴上,点N在坐标平面内,若四边形MFDN
是菱形,则菱形MFDN的面积
是_______.
M
N
