人教版数学八年级下册20.1.1 平均数 课件(20张PPT)
文档属性
| 名称 | 人教版数学八年级下册20.1.1 平均数 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 18:50:14 | ||
图片预览



文档简介
(共20张PPT)
20.1.1平均数
请在此输入您的副标题
【情景引入】
问题1:我们刚刚结束的一次篮球课中,我们班男生平均投中了9个,女生平均投中了3个,你能计算出我们班的平均投中的个数吗?
平均数7.2称为个数9和3的加权平均数(weighted average);
对应的人数35和15分别为个数9和3的权(weight).
班级平均投中个数 (个)
×
【实际运用】
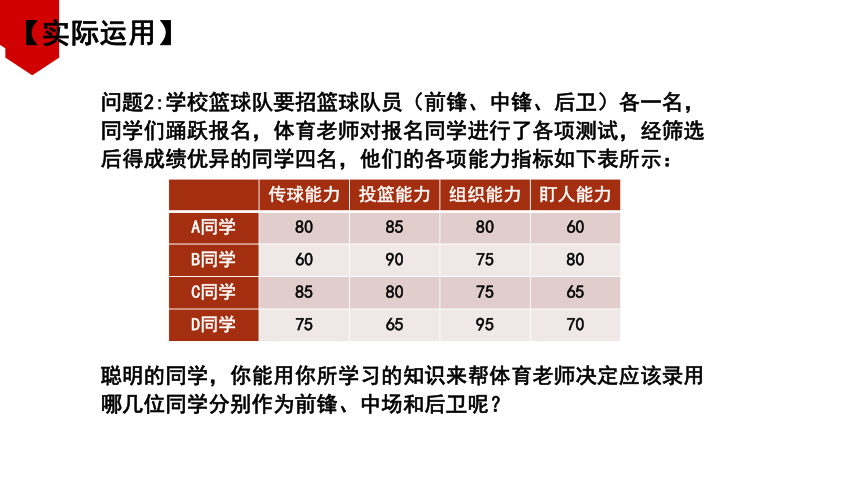
问题2:学校篮球队要招篮球队员(前锋、中锋、后卫)各一名,同学们踊跃报名,体育老师对报名同学进行了各项测试,经筛选后得成绩优异的同学四名,他们的各项能力指标如下表所示:
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
聪明的同学,你能用你所学习的知识来帮体育老师决定应该录用哪几位同学分别作为前锋、中场和后卫呢?
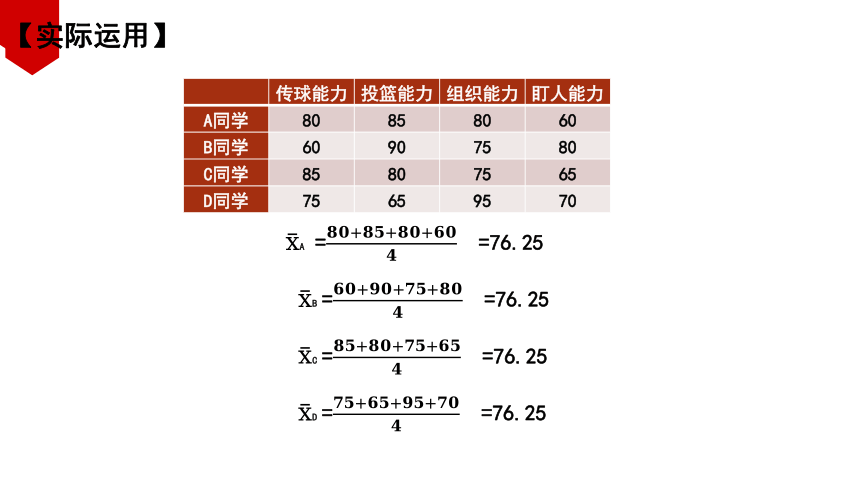
【实际运用】
A = =76.25
B = =76.25
C = =76.25
D = =76.25
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
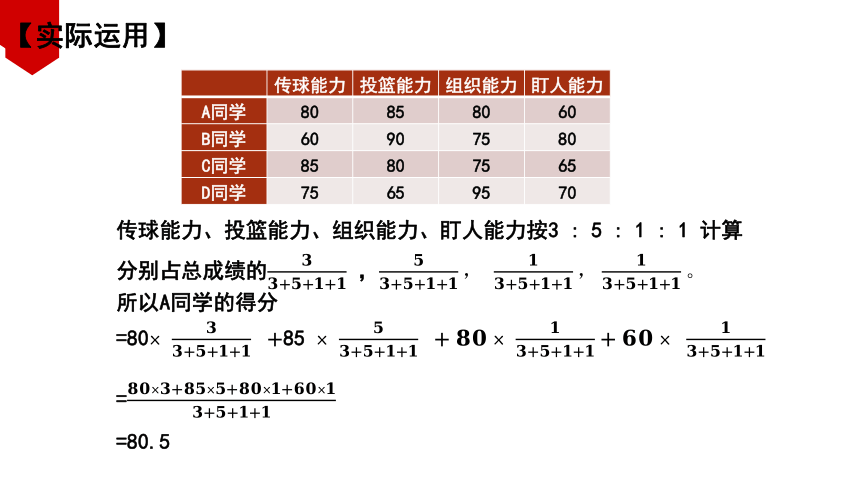
【实际运用】
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
传球能力、投篮能力、组织能力、盯人能力按3 : 5 : 1 : 1 计算
分别占总成绩的 ,
所以A同学的得分
=80 85
=
=80.5
【实际运用】
所以A同学的得分 = =80.5
所以B同学的得分 = =78.5
所以C同学的得分 = =79.5
所以D同学的得分 = =71.5
所以我是体育老师我选A同学作为前锋。
权(weight)
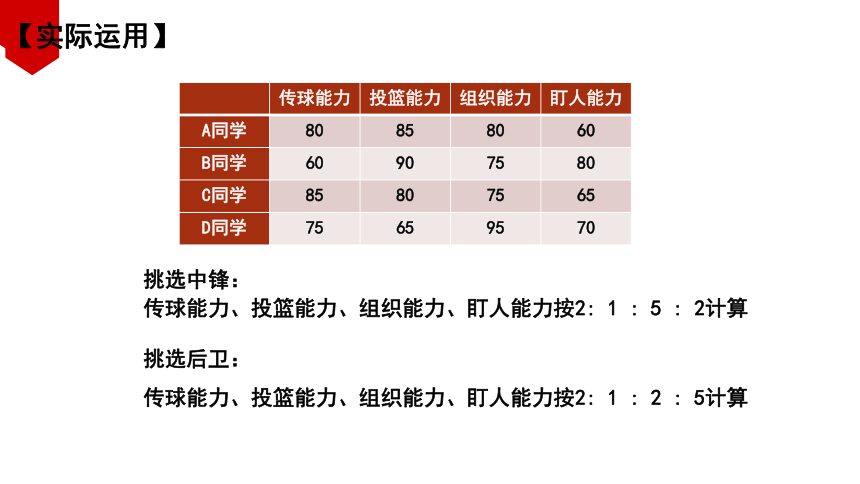
【实际运用】
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
挑选后卫:
传球能力、投篮能力、组织能力、盯人能力按2: 1 : 2 : 5计算
挑选中锋:
传球能力、投篮能力、组织能力、盯人能力按2: 1 : 5 : 2计算
【实际运用】
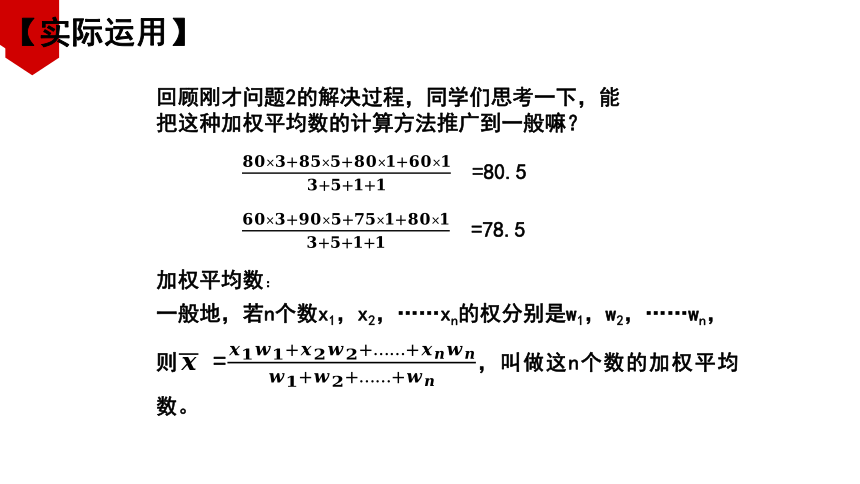
=80.5
=78.5
回顾刚才问题2的解决过程,同学们思考一下,能把这种加权平均数的计算方法推广到一般嘛?
加权平均数:
一般地,若n个数x1,x2,……xn的权分别是w1,w2,……wn,
则 =,叫做这n个数的加权平均数。
【实际运用】
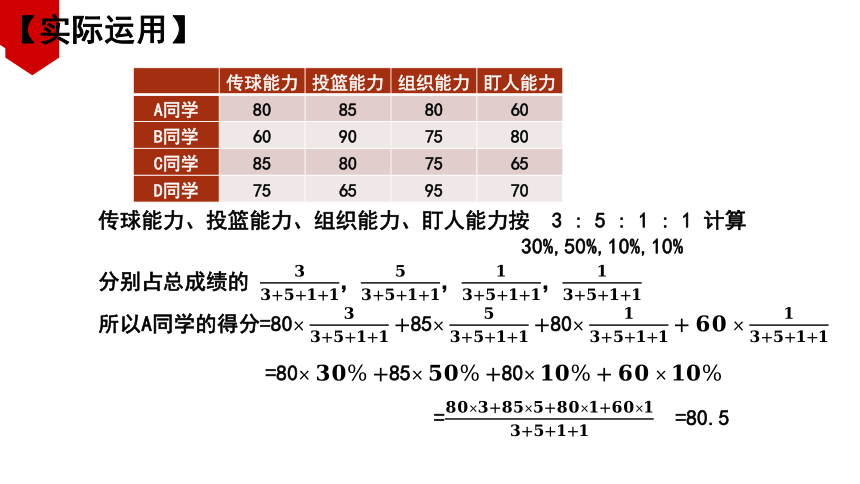
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
传球能力、投篮能力、组织能力、盯人能力按 3 : 5 : 1 : 1 计算
分别占总成绩的 ,,,
所以A同学的得分=808580
= =80.5
30%,50%,10%,10%
=808580
【概念辨析】
问题3:结合上面两个例子, 它与求算术平均数有何区别和联系?
区别:加权平均数不仅要考虑各个数据,还要考虑它们的重要性
联系:如果一组数据中各个数据重要程度相同,
即 w1=w2=……=wn,不妨设w1=w2=……=wn=w,
则 ==
所以算术平均数是加权平均数的一种特殊情况。
1.频数的形式:如:35、15
权的出现形式
2.比的形式:3:5:1:1
3.百分比的形式:如:30%,50%,10%,10%
互相
转化
【自主探索 应用设计】
说说我心中的球星!
科比
前美国职业篮球运动员,整个NBA生涯都效力于洛杉矶湖人队, 2020年1月27日,因直升机事故遇难,享年41岁。
5夺NBA总冠军;
2次总决赛MVP;
4次全明星赛MVP;
共18次入选NBA全明星阵容;
15次入选 NBA 最佳阵容;
12次入选 NBA 最佳防守阵容;
国家队生涯两夺奥运会金牌
勒布朗·詹姆斯
勒布朗·詹姆斯是继乔丹、皮蓬后又一个在同一年拿到奥运金牌和总冠军的球员,同时还成为历史上第二个在同一年揽得NBA总冠军、总决赛MVP和奥运金牌的球员并连续六年进入NBA总决赛,创历史记录!
【课外自主作业】
1、列出多名你心目中的优秀球星,上网查资料,收集他们篮球生涯的各项数据;
2、做成一张表格,理性的给你收集的各项数据加权;
3、算出加权平均数,最高者为MVP。
选出你心中的MVP!(Most Valuable Player)
【巩固练习】
问题5:为了解某市九年级学生开展“综合与实践”活动的情况,抽样调查了该市200名九年级学生上学期参加综合与实践活动的天数,并根据调查所得的数据绘制条形统计图如下.
求这200名学生参加“综合与实践”活动的每人的平均天数.
30
0
20
60
50
40
10
6天
2天
3天
4天
5天
天数
追问:这道题中的权是什么
每人平均练习的时间为4.25。
人数10、30、60、50、50分别是时间2、 3、 4、 5、6 的权。
【巩固练习】
问题6:小明统计了15天同一时间段通过某路口的汽车流量如下(单位:辆).求这15天在这个时间段通过该路口的汽车每天平均流量.
汽车流量 142 145 157 156
天数 2 2 5 6
追问:这道题中的权是什么
天数2、2、5、6分别是时间流量142、 145、 157、 156 的权。
平均流量为153。
【巩固练习】
问题7:某校食堂销售三种午餐盒饭的有关数据如图所示,求该食堂销售午餐每盒盒饭的平均价格.
8元
15%
6元
60%
5元
25%
追问:这道题中的权是什么
百分数25%、60%、15%分别是价格5、 6、 8的权。
平均流量为。
【回顾与总结】
=
w1=w2=……=wn=w
根据各个数据的重要程度,所分别赋予的量化值
频数、比、百分数
能够反映的数据的相对“重要程度”。
n个数x1,x2,……xn的权分别是w1,w2,……wn则 =
【课后作业】
某食品店将甲,乙,丙3种糖果按质量5:4:1的比配置成一种什锦糖,已知甲,乙,丙三种糖果每千克的零售价分别为16元,20元,27元.
(1) 商家准备把这种什锦糖果按单价的算术平均数来就定价,你认为合理吗?说说你的看法.
(2)如果商家配置什锦糖果,使甲乙丙三种质量相等,你将如何定价?
【课后作业】
同学们 再见!
20.1.1平均数
请在此输入您的副标题
【情景引入】
问题1:我们刚刚结束的一次篮球课中,我们班男生平均投中了9个,女生平均投中了3个,你能计算出我们班的平均投中的个数吗?
平均数7.2称为个数9和3的加权平均数(weighted average);
对应的人数35和15分别为个数9和3的权(weight).
班级平均投中个数 (个)
×
【实际运用】
问题2:学校篮球队要招篮球队员(前锋、中锋、后卫)各一名,同学们踊跃报名,体育老师对报名同学进行了各项测试,经筛选后得成绩优异的同学四名,他们的各项能力指标如下表所示:
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
聪明的同学,你能用你所学习的知识来帮体育老师决定应该录用哪几位同学分别作为前锋、中场和后卫呢?
【实际运用】
A = =76.25
B = =76.25
C = =76.25
D = =76.25
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
【实际运用】
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
传球能力、投篮能力、组织能力、盯人能力按3 : 5 : 1 : 1 计算
分别占总成绩的 ,
所以A同学的得分
=80 85
=
=80.5
【实际运用】
所以A同学的得分 = =80.5
所以B同学的得分 = =78.5
所以C同学的得分 = =79.5
所以D同学的得分 = =71.5
所以我是体育老师我选A同学作为前锋。
权(weight)
【实际运用】
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
挑选后卫:
传球能力、投篮能力、组织能力、盯人能力按2: 1 : 2 : 5计算
挑选中锋:
传球能力、投篮能力、组织能力、盯人能力按2: 1 : 5 : 2计算
【实际运用】
=80.5
=78.5
回顾刚才问题2的解决过程,同学们思考一下,能把这种加权平均数的计算方法推广到一般嘛?
加权平均数:
一般地,若n个数x1,x2,……xn的权分别是w1,w2,……wn,
则 =,叫做这n个数的加权平均数。
【实际运用】
传球能力 投篮能力 组织能力 盯人能力
A同学 80 85 80 60
B同学 60 90 75 80
C同学 85 80 75 65
D同学 75 65 95 70
传球能力、投篮能力、组织能力、盯人能力按 3 : 5 : 1 : 1 计算
分别占总成绩的 ,,,
所以A同学的得分=808580
= =80.5
30%,50%,10%,10%
=808580
【概念辨析】
问题3:结合上面两个例子, 它与求算术平均数有何区别和联系?
区别:加权平均数不仅要考虑各个数据,还要考虑它们的重要性
联系:如果一组数据中各个数据重要程度相同,
即 w1=w2=……=wn,不妨设w1=w2=……=wn=w,
则 ==
所以算术平均数是加权平均数的一种特殊情况。
1.频数的形式:如:35、15
权的出现形式
2.比的形式:3:5:1:1
3.百分比的形式:如:30%,50%,10%,10%
互相
转化
【自主探索 应用设计】
说说我心中的球星!
科比
前美国职业篮球运动员,整个NBA生涯都效力于洛杉矶湖人队, 2020年1月27日,因直升机事故遇难,享年41岁。
5夺NBA总冠军;
2次总决赛MVP;
4次全明星赛MVP;
共18次入选NBA全明星阵容;
15次入选 NBA 最佳阵容;
12次入选 NBA 最佳防守阵容;
国家队生涯两夺奥运会金牌
勒布朗·詹姆斯
勒布朗·詹姆斯是继乔丹、皮蓬后又一个在同一年拿到奥运金牌和总冠军的球员,同时还成为历史上第二个在同一年揽得NBA总冠军、总决赛MVP和奥运金牌的球员并连续六年进入NBA总决赛,创历史记录!
【课外自主作业】
1、列出多名你心目中的优秀球星,上网查资料,收集他们篮球生涯的各项数据;
2、做成一张表格,理性的给你收集的各项数据加权;
3、算出加权平均数,最高者为MVP。
选出你心中的MVP!(Most Valuable Player)
【巩固练习】
问题5:为了解某市九年级学生开展“综合与实践”活动的情况,抽样调查了该市200名九年级学生上学期参加综合与实践活动的天数,并根据调查所得的数据绘制条形统计图如下.
求这200名学生参加“综合与实践”活动的每人的平均天数.
30
0
20
60
50
40
10
6天
2天
3天
4天
5天
天数
追问:这道题中的权是什么
每人平均练习的时间为4.25。
人数10、30、60、50、50分别是时间2、 3、 4、 5、6 的权。
【巩固练习】
问题6:小明统计了15天同一时间段通过某路口的汽车流量如下(单位:辆).求这15天在这个时间段通过该路口的汽车每天平均流量.
汽车流量 142 145 157 156
天数 2 2 5 6
追问:这道题中的权是什么
天数2、2、5、6分别是时间流量142、 145、 157、 156 的权。
平均流量为153。
【巩固练习】
问题7:某校食堂销售三种午餐盒饭的有关数据如图所示,求该食堂销售午餐每盒盒饭的平均价格.
8元
15%
6元
60%
5元
25%
追问:这道题中的权是什么
百分数25%、60%、15%分别是价格5、 6、 8的权。
平均流量为。
【回顾与总结】
=
w1=w2=……=wn=w
根据各个数据的重要程度,所分别赋予的量化值
频数、比、百分数
能够反映的数据的相对“重要程度”。
n个数x1,x2,……xn的权分别是w1,w2,……wn则 =
【课后作业】
某食品店将甲,乙,丙3种糖果按质量5:4:1的比配置成一种什锦糖,已知甲,乙,丙三种糖果每千克的零售价分别为16元,20元,27元.
(1) 商家准备把这种什锦糖果按单价的算术平均数来就定价,你认为合理吗?说说你的看法.
(2)如果商家配置什锦糖果,使甲乙丙三种质量相等,你将如何定价?
【课后作业】
同学们 再见!
