人教版数学七年级下册7.2.1用坐标表示地理位置 习题(含答案)
文档属性
| 名称 | 人教版数学七年级下册7.2.1用坐标表示地理位置 习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 505.1KB | ||
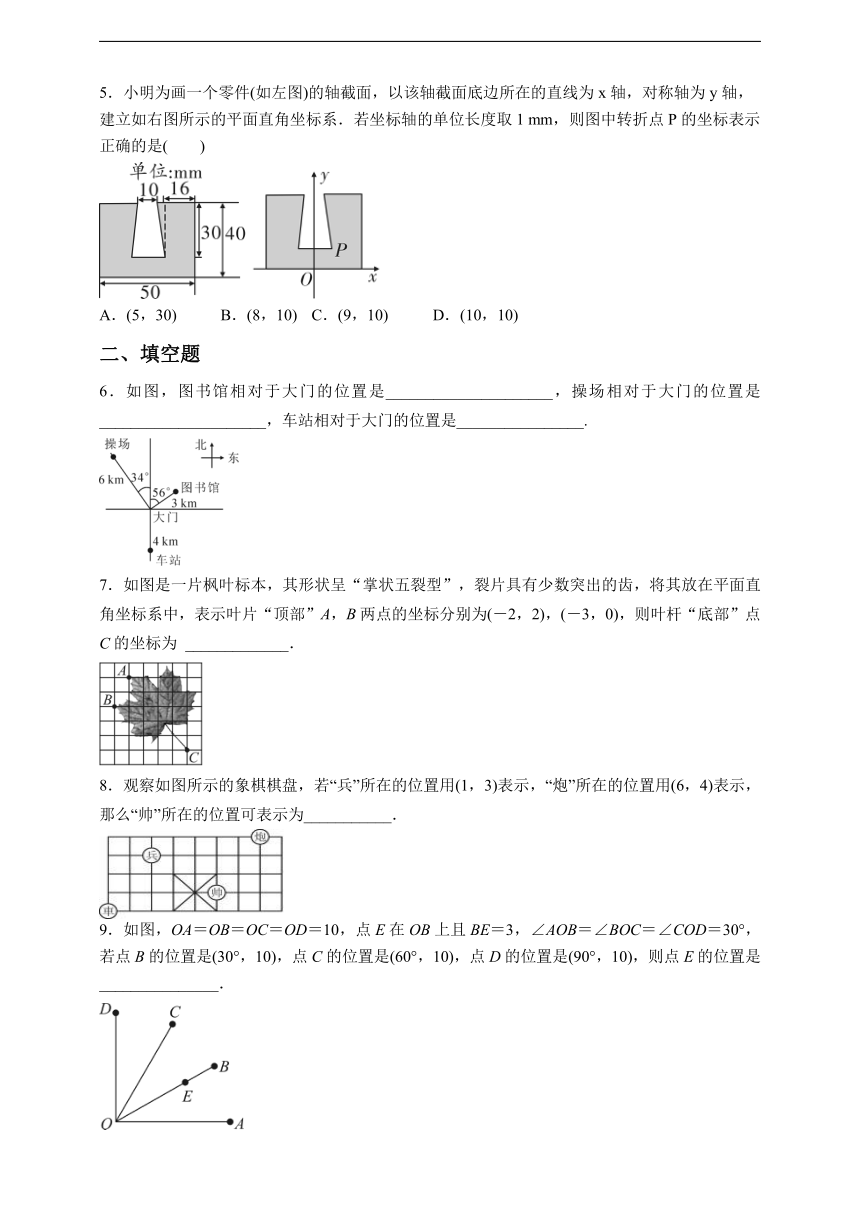
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-21 22:10:12 | ||
图片预览



文档简介
7.2.1 用坐标表示地理位置
一、选择题
1.如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,并且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是( )
A.(1,1) B.(1,2) C.(2,1) D.(2,2)
2.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是( )
A.(2,-1) B.(4,-2) C.(4,2) D.(2,0)
3.点A的位置如图所示,则关于点A的位置下列说法中正确的是( )
A.距点O 4 km处 B.北偏东40°方向上4 km处
C.在点O北偏东50°方向上4 km处 D.在点O北偏东40°方向上4 km处
4.如图,已知两点M(-2,2),N(1,-1),则A,B,C三个点中为坐标原点的是( )
A.点A B.点B C.点C D.以上都不对
5.小明为画一个零件(如左图)的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如右图所示的平面直角坐标系.若坐标轴的单位长度取1 mm,则图中转折点P的坐标表示正确的是( )
A.(5,30) B.(8,10) C.(9,10) D.(10,10)
二、填空题
6.如图,图书馆相对于大门的位置是_____________________,操场相对于大门的位置是_____________________,车站相对于大门的位置是________________.
7.如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 _____________.
8.观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为___________.
9.如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是_______________.
10.如图,一个机器人从点O出发,向正东方向走3 m到达点A1,再向正北方向走6 m到达点A2,再向正西方向走9 m到达点A3,再向正南方向走12 m到达点A4,再向正东方向走15 m到达点A5,按如此规律走下去,并且以点O为原点,以1 m为单位长度,正东方向为x轴正方向,正北方向为y轴正方向建立平面直角坐标系,当机器人走到点A10时,A10的坐标是 .
三、解答题
11.小兰和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图(如图),可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园的位置D的坐标为(2,-2),你能帮她求出其他各景点所在位置的坐标吗?
12.如图标出了李明家附近的一些地方.
(1)根据图中所建立的平面直角坐标系,写出学校、邮局的坐标;
(2)某星期日早晨,李明从家里出发,沿着(-2,-1),(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),(0,-1)的路线转了一下,写出他路上经过的地方;
(3)连接他在(2)中经过的地点,你能得到什么图形?
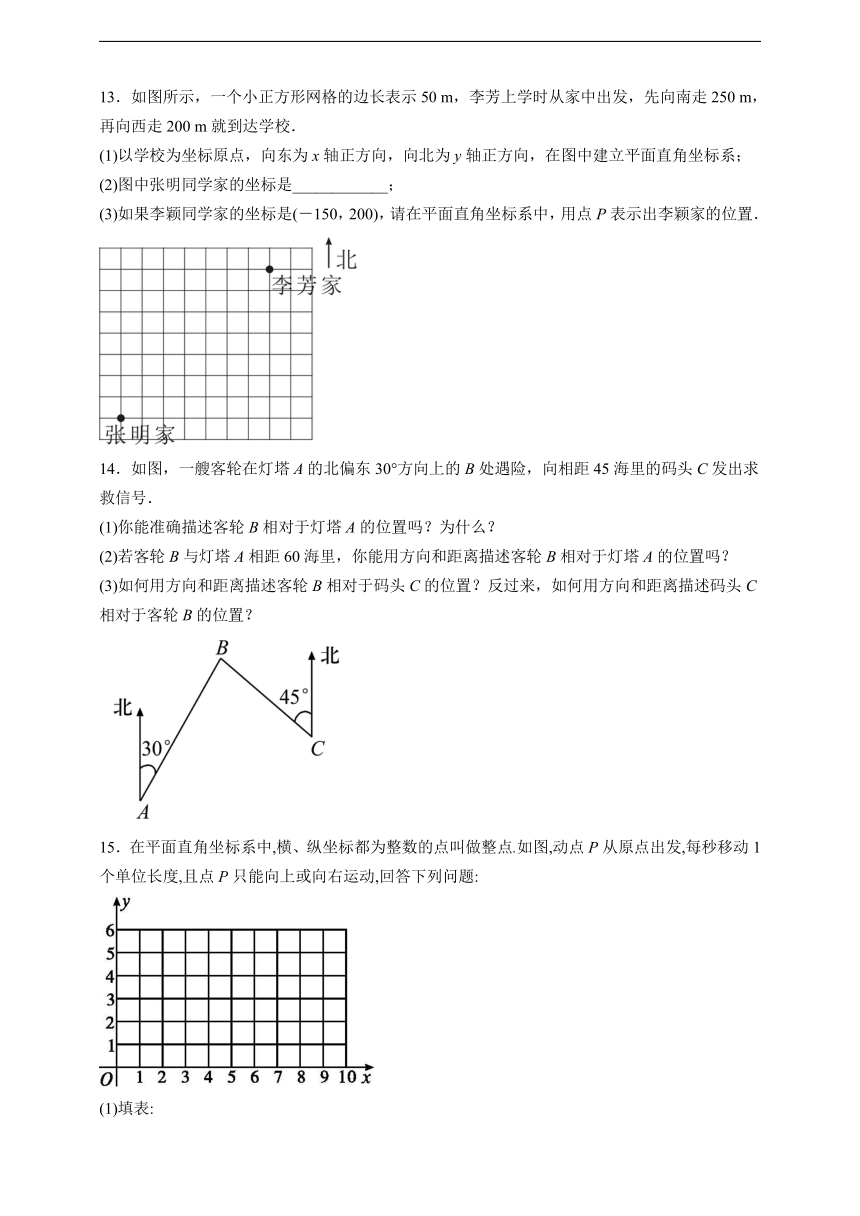
13.如图所示,一个小正方形网格的边长表示50 m,李芳上学时从家中出发,先向南走250 m,再向西走200 m就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系;
(2)图中张明同学家的坐标是____________;
(3)如果李颖同学家的坐标是(-150,200),请在平面直角坐标系中,用点P表示出李颖家的位置.
14.如图,一艘客轮在灯塔A的北偏东30°方向上的B处遇险,向相距45海里的码头C发出求救信号.
(1)你能准确描述客轮B相对于灯塔A的位置吗?为什么?
(2)若客轮B与灯塔A相距60海里,你能用方向和距离描述客轮B相对于灯塔A的位置吗?
(3)如何用方向和距离描述客轮B相对于码头C的位置?反过来,如何用方向和距离描述码头C相对于客轮B的位置?
15.在平面直角坐标系中,横、纵坐标都为整数的点叫做整点.如图,动点P从原点出发,每秒移动1个单位长度,且点P只能向上或向右运动,回答下列问题:
(1)填表:
P从原点出发时间t 1秒 2秒 3秒 4秒
可得到的整点坐标 (1,0) (0,1) (2,0) (0,2) (1,1)
整点个数n
(2)点P从原点出发10秒时,可得到的整点个数为多少
(3)当点P从原点出发多少秒时,可到达点(10,5)
参考答案
一、选择题
1.如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,并且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是( D )
A.(1,1) B.(1,2) C.(2,1) D.(2,2)
2.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是( A )
A.(2,-1) B.(4,-2) C.(4,2) D.(2,0)
3.点A的位置如图所示,则关于点A的位置下列说法中正确的是( D )
A.距点O 4 km处 B.北偏东40°方向上4 km处
C.在点O北偏东50°方向上4 km处 D.在点O北偏东40°方向上4 km处
4.如图,已知两点M(-2,2),N(1,-1),则A,B,C三个点中为坐标原点的是( A )
A.点A B.点B C.点C D.以上都不对
5.小明为画一个零件(如左图)的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如右图所示的平面直角坐标系.若坐标轴的单位长度取1 mm,则图中转折点P的坐标表示正确的是( C )
A.(5,30) B.(8,10) C.(9,10) D.(10,10)
二、填空题
6.如图,图书馆相对于大门的位置是_____________________,操场相对于大门的位置是_____________________,车站相对于大门的位置是________________.
【答案】北偏东56°,3 km 北偏西34°,6 km 正南,4 km
7.如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 _____________.
【答案】(2,-3)
8.观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为___________.
【答案】(4,1)
9.如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是_______________.
【答案】(30°,7)
10.如图,一个机器人从点O出发,向正东方向走3 m到达点A1,再向正北方向走6 m到达点A2,再向正西方向走9 m到达点A3,再向正南方向走12 m到达点A4,再向正东方向走15 m到达点A5,按如此规律走下去,并且以点O为原点,以1 m为单位长度,正东方向为x轴正方向,正北方向为y轴正方向建立平面直角坐标系,当机器人走到点A10时,A10的坐标是 .
【答案】(15,18)
三、解答题
11.小兰和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图(如图),可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园的位置D的坐标为(2,-2),你能帮她求出其他各景点所在位置的坐标吗?
解:由题意可知,完整的平面直角坐标系如图.则音乐台的位置A(0,4),湖心亭的位置B(-3,2),望春亭的位置C(-2,-2),牡丹园的位置E(3,3)
12.如图标出了李明家附近的一些地方.
(1)根据图中所建立的平面直角坐标系,写出学校、邮局的坐标;
(2)某星期日早晨,李明从家里出发,沿着(-2,-1),(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),(0,-1)的路线转了一下,写出他路上经过的地方;
(3)连接他在(2)中经过的地点,你能得到什么图形?
解:(1)学校(1,3),邮局(0,-1)
(2)李明家→商店→公园→汽车站→水果店→学校→游乐场→邮局
(3)一艘帆船
13.如图所示,一个小正方形网格的边长表示50 m,李芳上学时从家中出发,先向南走250 m,再向西走200 m就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系;
(2)图中张明同学家的坐标是____________;
(3)如果李颖同学家的坐标是(-150,200),请在平面直角坐标系中,用点P表示出李颖家的位置.
解:(1)如图所示
(2)张明同学家的坐标是(-150,-100)
(3)如图所示,点P即为所求
14.如图,一艘客轮在灯塔A的北偏东30°方向上的B处遇险,向相距45海里的码头C发出求救信号.
(1)你能准确描述客轮B相对于灯塔A的位置吗?为什么?
(2)若客轮B与灯塔A相距60海里,你能用方向和距离描述客轮B相对于灯塔A的位置吗?
(3)如何用方向和距离描述客轮B相对于码头C的位置?反过来,如何用方向和距离描述码头C相对于客轮B的位置?
解:(1)不能,因为表示平面内的点一般需要两个数据,只有一个数据无法确定物体的位置
(2)能,客轮B在灯塔A的北偏东30°,相距60海里处
(3)客轮B在码头C的北偏西45°,相距45海里处;码头C在客轮B的南偏东45°,相距45海里处
15.在平面直角坐标系中,横、纵坐标都为整数的点叫做整点.如图,动点P从原点出发,每秒移动1个单位长度,且点P只能向上或向右运动,回答下列问题:
(1)填表:
P从原点出发时间t 1秒 2秒 3秒 4秒
可得到的整点坐标 (1,0) (0,1) (2,0) (0,2) (1,1)
整点个数n
(2)点P从原点出发10秒时,可得到的整点个数为多少
(3)当点P从原点出发多少秒时,可到达点(10,5)
解 (1)1秒:2 2秒:3
3秒:(3,0),(0,3),(1,2),(2,1) 4
4秒:(4,0),(0,4),(1,3),(3,1),(2,2) 5
(2)11. (3)15秒.
一、选择题
1.如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,并且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是( )
A.(1,1) B.(1,2) C.(2,1) D.(2,2)
2.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是( )
A.(2,-1) B.(4,-2) C.(4,2) D.(2,0)
3.点A的位置如图所示,则关于点A的位置下列说法中正确的是( )
A.距点O 4 km处 B.北偏东40°方向上4 km处
C.在点O北偏东50°方向上4 km处 D.在点O北偏东40°方向上4 km处
4.如图,已知两点M(-2,2),N(1,-1),则A,B,C三个点中为坐标原点的是( )
A.点A B.点B C.点C D.以上都不对
5.小明为画一个零件(如左图)的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如右图所示的平面直角坐标系.若坐标轴的单位长度取1 mm,则图中转折点P的坐标表示正确的是( )
A.(5,30) B.(8,10) C.(9,10) D.(10,10)
二、填空题
6.如图,图书馆相对于大门的位置是_____________________,操场相对于大门的位置是_____________________,车站相对于大门的位置是________________.
7.如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 _____________.
8.观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为___________.
9.如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是_______________.
10.如图,一个机器人从点O出发,向正东方向走3 m到达点A1,再向正北方向走6 m到达点A2,再向正西方向走9 m到达点A3,再向正南方向走12 m到达点A4,再向正东方向走15 m到达点A5,按如此规律走下去,并且以点O为原点,以1 m为单位长度,正东方向为x轴正方向,正北方向为y轴正方向建立平面直角坐标系,当机器人走到点A10时,A10的坐标是 .
三、解答题
11.小兰和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图(如图),可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园的位置D的坐标为(2,-2),你能帮她求出其他各景点所在位置的坐标吗?
12.如图标出了李明家附近的一些地方.
(1)根据图中所建立的平面直角坐标系,写出学校、邮局的坐标;
(2)某星期日早晨,李明从家里出发,沿着(-2,-1),(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),(0,-1)的路线转了一下,写出他路上经过的地方;
(3)连接他在(2)中经过的地点,你能得到什么图形?
13.如图所示,一个小正方形网格的边长表示50 m,李芳上学时从家中出发,先向南走250 m,再向西走200 m就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系;
(2)图中张明同学家的坐标是____________;
(3)如果李颖同学家的坐标是(-150,200),请在平面直角坐标系中,用点P表示出李颖家的位置.
14.如图,一艘客轮在灯塔A的北偏东30°方向上的B处遇险,向相距45海里的码头C发出求救信号.
(1)你能准确描述客轮B相对于灯塔A的位置吗?为什么?
(2)若客轮B与灯塔A相距60海里,你能用方向和距离描述客轮B相对于灯塔A的位置吗?
(3)如何用方向和距离描述客轮B相对于码头C的位置?反过来,如何用方向和距离描述码头C相对于客轮B的位置?
15.在平面直角坐标系中,横、纵坐标都为整数的点叫做整点.如图,动点P从原点出发,每秒移动1个单位长度,且点P只能向上或向右运动,回答下列问题:
(1)填表:
P从原点出发时间t 1秒 2秒 3秒 4秒
可得到的整点坐标 (1,0) (0,1) (2,0) (0,2) (1,1)
整点个数n
(2)点P从原点出发10秒时,可得到的整点个数为多少
(3)当点P从原点出发多少秒时,可到达点(10,5)
参考答案
一、选择题
1.如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,并且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是( D )
A.(1,1) B.(1,2) C.(2,1) D.(2,2)
2.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是( A )
A.(2,-1) B.(4,-2) C.(4,2) D.(2,0)
3.点A的位置如图所示,则关于点A的位置下列说法中正确的是( D )
A.距点O 4 km处 B.北偏东40°方向上4 km处
C.在点O北偏东50°方向上4 km处 D.在点O北偏东40°方向上4 km处
4.如图,已知两点M(-2,2),N(1,-1),则A,B,C三个点中为坐标原点的是( A )
A.点A B.点B C.点C D.以上都不对
5.小明为画一个零件(如左图)的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如右图所示的平面直角坐标系.若坐标轴的单位长度取1 mm,则图中转折点P的坐标表示正确的是( C )
A.(5,30) B.(8,10) C.(9,10) D.(10,10)
二、填空题
6.如图,图书馆相对于大门的位置是_____________________,操场相对于大门的位置是_____________________,车站相对于大门的位置是________________.
【答案】北偏东56°,3 km 北偏西34°,6 km 正南,4 km
7.如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 _____________.
【答案】(2,-3)
8.观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为___________.
【答案】(4,1)
9.如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是_______________.
【答案】(30°,7)
10.如图,一个机器人从点O出发,向正东方向走3 m到达点A1,再向正北方向走6 m到达点A2,再向正西方向走9 m到达点A3,再向正南方向走12 m到达点A4,再向正东方向走15 m到达点A5,按如此规律走下去,并且以点O为原点,以1 m为单位长度,正东方向为x轴正方向,正北方向为y轴正方向建立平面直角坐标系,当机器人走到点A10时,A10的坐标是 .
【答案】(15,18)
三、解答题
11.小兰和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图(如图),可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园的位置D的坐标为(2,-2),你能帮她求出其他各景点所在位置的坐标吗?
解:由题意可知,完整的平面直角坐标系如图.则音乐台的位置A(0,4),湖心亭的位置B(-3,2),望春亭的位置C(-2,-2),牡丹园的位置E(3,3)
12.如图标出了李明家附近的一些地方.
(1)根据图中所建立的平面直角坐标系,写出学校、邮局的坐标;
(2)某星期日早晨,李明从家里出发,沿着(-2,-1),(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),(0,-1)的路线转了一下,写出他路上经过的地方;
(3)连接他在(2)中经过的地点,你能得到什么图形?
解:(1)学校(1,3),邮局(0,-1)
(2)李明家→商店→公园→汽车站→水果店→学校→游乐场→邮局
(3)一艘帆船
13.如图所示,一个小正方形网格的边长表示50 m,李芳上学时从家中出发,先向南走250 m,再向西走200 m就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系;
(2)图中张明同学家的坐标是____________;
(3)如果李颖同学家的坐标是(-150,200),请在平面直角坐标系中,用点P表示出李颖家的位置.
解:(1)如图所示
(2)张明同学家的坐标是(-150,-100)
(3)如图所示,点P即为所求
14.如图,一艘客轮在灯塔A的北偏东30°方向上的B处遇险,向相距45海里的码头C发出求救信号.
(1)你能准确描述客轮B相对于灯塔A的位置吗?为什么?
(2)若客轮B与灯塔A相距60海里,你能用方向和距离描述客轮B相对于灯塔A的位置吗?
(3)如何用方向和距离描述客轮B相对于码头C的位置?反过来,如何用方向和距离描述码头C相对于客轮B的位置?
解:(1)不能,因为表示平面内的点一般需要两个数据,只有一个数据无法确定物体的位置
(2)能,客轮B在灯塔A的北偏东30°,相距60海里处
(3)客轮B在码头C的北偏西45°,相距45海里处;码头C在客轮B的南偏东45°,相距45海里处
15.在平面直角坐标系中,横、纵坐标都为整数的点叫做整点.如图,动点P从原点出发,每秒移动1个单位长度,且点P只能向上或向右运动,回答下列问题:
(1)填表:
P从原点出发时间t 1秒 2秒 3秒 4秒
可得到的整点坐标 (1,0) (0,1) (2,0) (0,2) (1,1)
整点个数n
(2)点P从原点出发10秒时,可得到的整点个数为多少
(3)当点P从原点出发多少秒时,可到达点(10,5)
解 (1)1秒:2 2秒:3
3秒:(3,0),(0,3),(1,2),(2,1) 4
4秒:(4,0),(0,4),(1,3),(3,1),(2,2) 5
(2)11. (3)15秒.
